Оптимальный способ погашения кредита
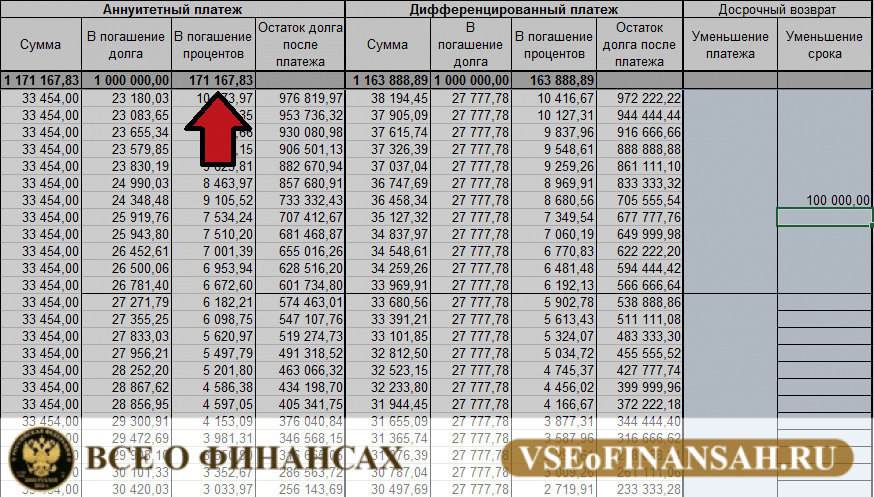
Заемщик при выборе кредитной программы должен знать, по какой схеме он будет погашать кредит: аннуитентными платежами- ежемесячно равными частями, включающие в себя сумму долга и проценты или дифференцированными (уменьшающимися) частями, процент начисялется на остаток задолженности.
Сегодня в мировой практике используется не менее десятка видов процентных ставок и способов начисления процентов по кредитам. Российские банки обычно предлагают своим заемщикам два способа погашения кредита: ежемесячные аннуитетные платежи и дифференцированные выплаты по фактическому остатку.
Игорь Садовский, первый заместитель председателя правления ЗАО «Банк ЖилФинанс», рассказывает, что коммерческие банки используют одну из четырех форм погашения кредита: дифференцированные платежи, аннуитетные платежи, платежи с выплатой процентов ежемесячно, а суммы кредита в конце срока, или же схему выплаты процентов по кредиту и суммы кредита в конце срока.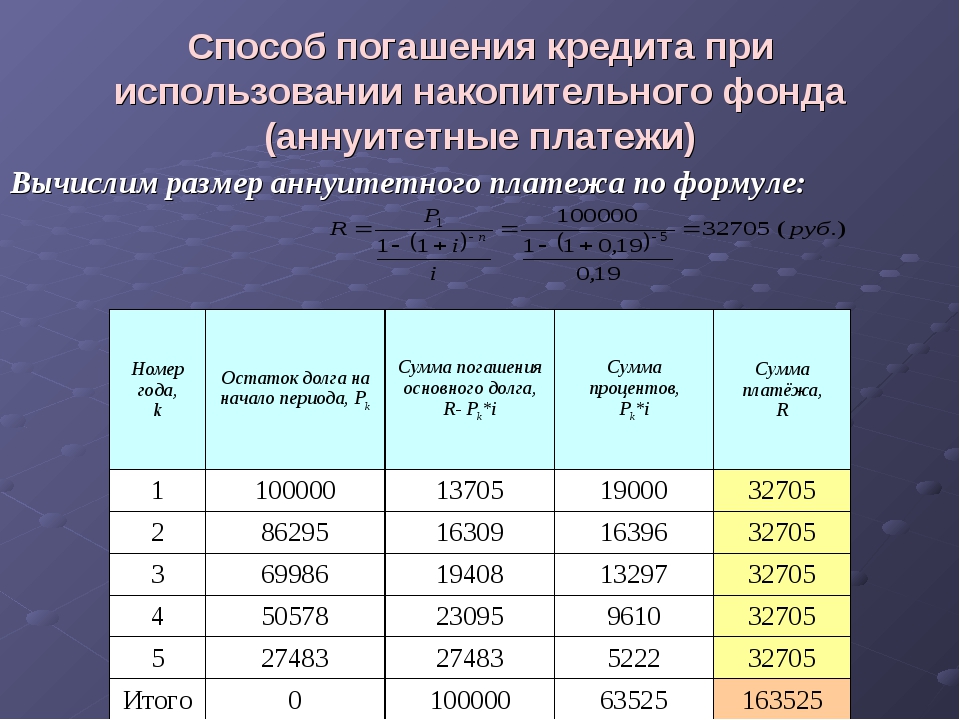
Вячеслав Пантелеев, начальник управления развития и сопровождения кредитных операций центра ипотечного кредитования БИНБанка, добавляет к этим способам, индивидуальные схемы погашения кредита.
Эксперты отмечают, что свои достоинства и недостатки есть как у аннуитетного, так и у дифференцированного способа погашения кредитов.
«Ежемесячные аннуитетные платежи проще и понятнее клиентам и являются наименее рискованными для банков. Индивидуальные схемы применяются в основном при сделках по улучшению клиентами своих жилищных условий, когда клиент получает кредит на покупку большей по площади квартиры и продает имеющуюся у него в собственности квартиру. В этом случае банк может оформить отсрочку в платежах по процентам и/или основному долгу на срок 3–6 месяцев», – поясняет Вячеслав Пантелеев.
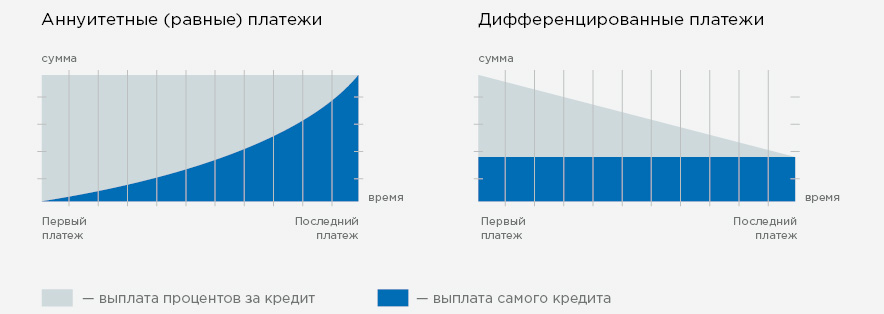
При аннуитетных выплатах фиксирована сама сумма, которую клиент вносит в банк. Она состоит из основного долга и процента. По мере истечения срока ссуды доля процента постепенно уменьшается, а основного долга – увеличивается. За счет этого платежи получаются равными.
Она состоит из основного долга и процента. По мере истечения срока ссуды доля процента постепенно уменьшается, а основного долга – увеличивается. За счет этого платежи получаются равными.
Игорь Садовский отмечает, что при дифференцированном платеже проценты за пользование кредитом с каждым последующим погашением уменьшаются, так как уменьшается сумма кредита.
«При погашении кредита аннуитетными платежами основной недостаток для клиента заключается в том, что сумма выплаченных процентов за весь срок обслуживания будет больше, чем при дифференцированных платежах. Разница появляется в связи с тем, что дифференцированные платежи позволяют выплачивать остаток задолженности по кредиту равномерно, при аннуитетных же платежах основная сумма платежа в начале срока обслуживания кредита будет направлена на погашение процентов, а погашение основного долга будет происходить медленнее», – рассказывает Вячеслав Пантелеев.
Дифференцированные платежи состоят из разделенного на весь период погашения тела кредита и переменной (убывающей) части процентов по нему, которая берется от суммы остатка. То есть при дифференцированных платежах сам кредит выплачивается равными долями в течение всего срока погашения. Таким образом, размер общего платежа каждый месяц уменьшается, а погашение основного долга равномерно распределено на весь срок кредита.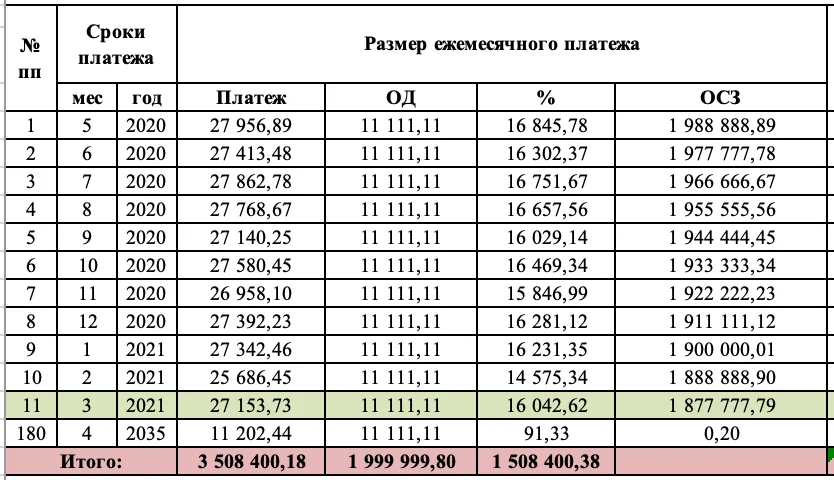
По мнению экспертов, дифференцированные платежи ложатся весьма тяжелым бременем на заемщика в первые годы расчетов по ипотечному кредиту. Зато приблизительно с середины срока кредитования эта нагрузка значительно снижается.
Вячеслав Пантелеев считает, что для банков более интересны кредиты, по которым клиенты производят аннуитетные ежемесячные платежи, поэтому в большинстве ведущих ипотечных банков используется исключительно эта схема платежей. По его словам, некоторые кредитные организации предлагают клиенту выбрать любую другую форму расчета.
«В конечном итоге, что выгодней для клиента – простота планирования семейного бюджета или снижение суммы процентных выплат по кредиту, необходимо решать в каждом отдельно взятом случае. Также стоить учитывать, что аннуитетная схема позволяет клиенту оформить большую сумму кредита, чем при использовании дифференцированных платежей, что достаточно актуально при нынешнем уровне цен на квартиры», – заключает банкир.
РБК.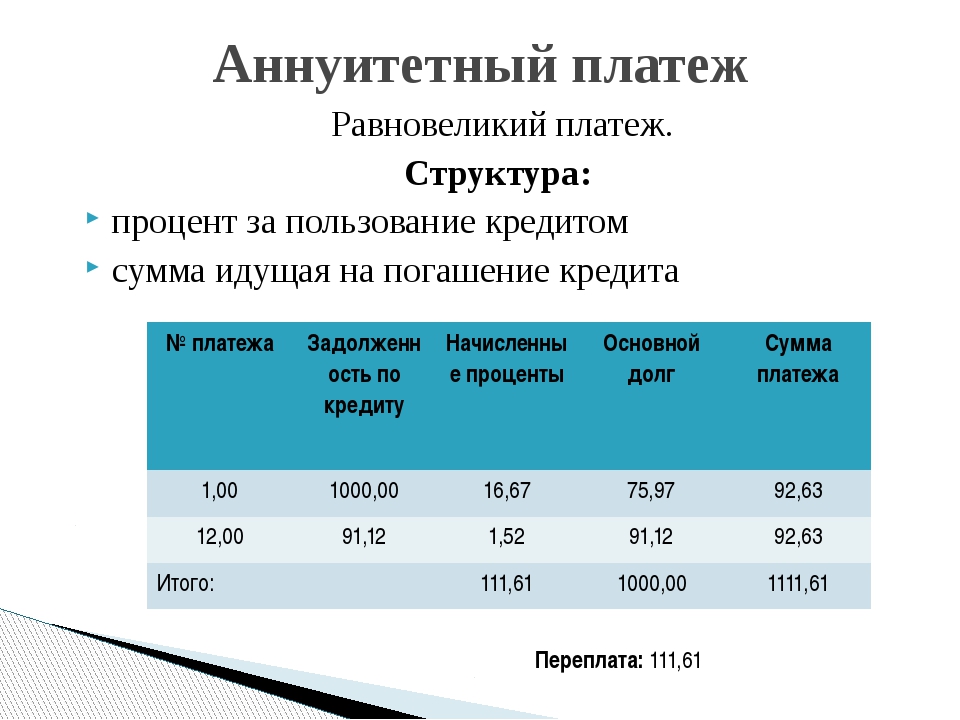 Личные Финансы, 05.10.2007
Личные Финансы, 05.10.2007
Людмила Виноградова
Аннуитет или дифференцированный платёж?
Принимая решение о том, чтобы взять кредит, особенно на крупную сумму, и особенно ипотечный, необходимо не только трезво оценивать свои возможности, но и уделить внимание выбору самого кредитного продукта, изучая условия в различных банках. Обратите внимание на способ погашения кредита. Платежи по погашению могут быть двух видов — аннуитетные (фиксированные) или дифференцированные.
Когда вы получите в банке график платежей, обратите внимание, какую часть от ежемесячных платежей по ипотеке составляют проценты в начале срока и в конце.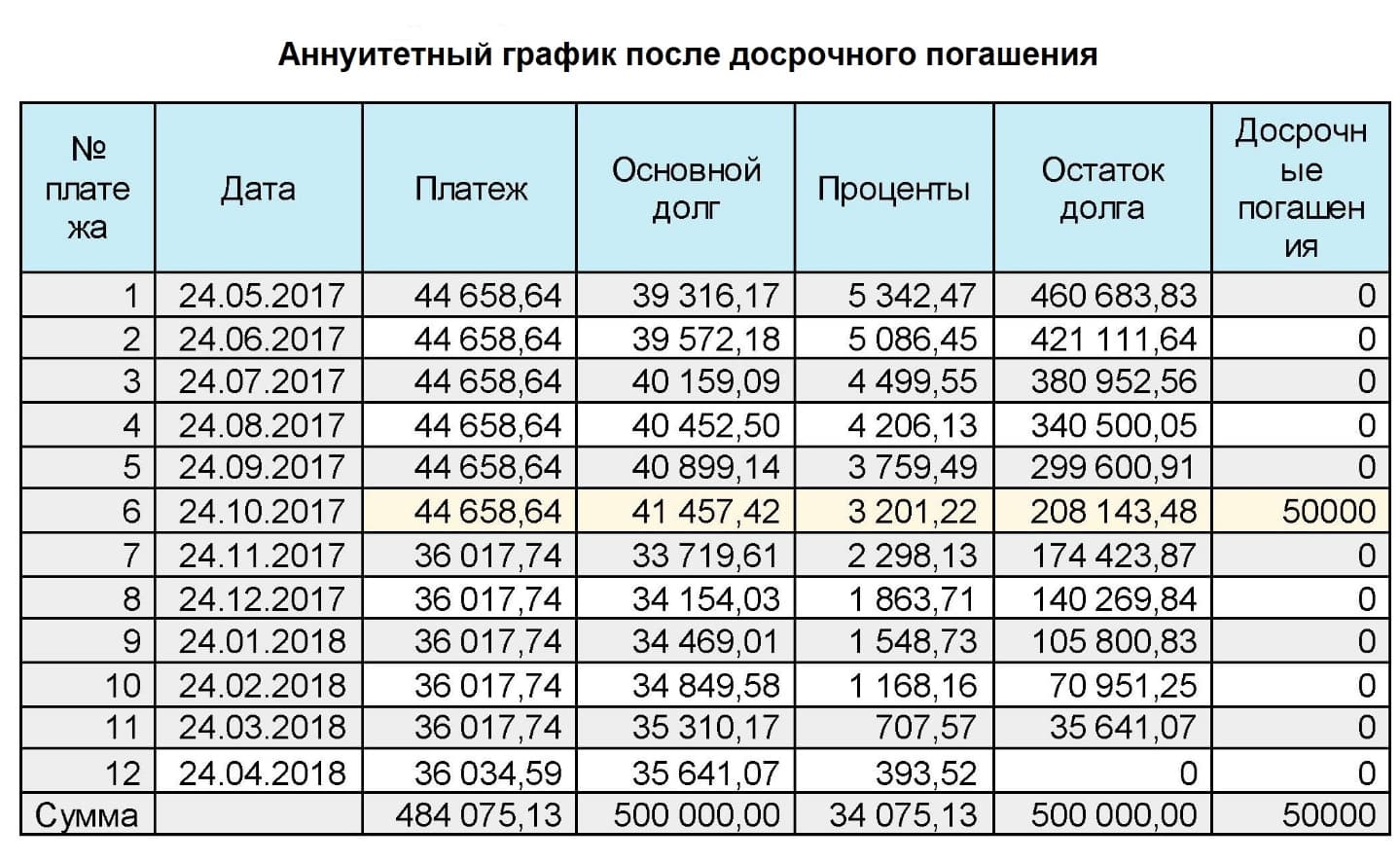
В большинстве случаев банки предлагают кредитные продукты с аннуитетным способом выплат. Дифференцированные платежи можно встретить в различных корпоративных и специальных кредитных программах.
Дифференцированный платёж — долг по кредиту гасится ежемесячно одинаковыми суммами, а размер процентов определяется исходя из невыплаченного остатка заёмных средств. Соответственно, выплаты к концу срока погашения кредита уменьшаются. При частичном досрочном погашении кредита, вы уменьшаете, прежде всего ежемесячный взнос, и во вторую очередь — срок погашения.
Общая сумма переплаты по займу с дифференциальными платежами будет меньше на 15—25 процентов. При значительных суммах кредита и длительном периоде погашения, особенно в случае ипотечного кредитования, эта разница будет существенна.
Если вы рассматриваете банковское предложение с правом выбора схемы платежей, стоит понимать, что в первые месяцы при дифференцированной схеме, платежи будут на 20—25% выше, чем при аннуитетной.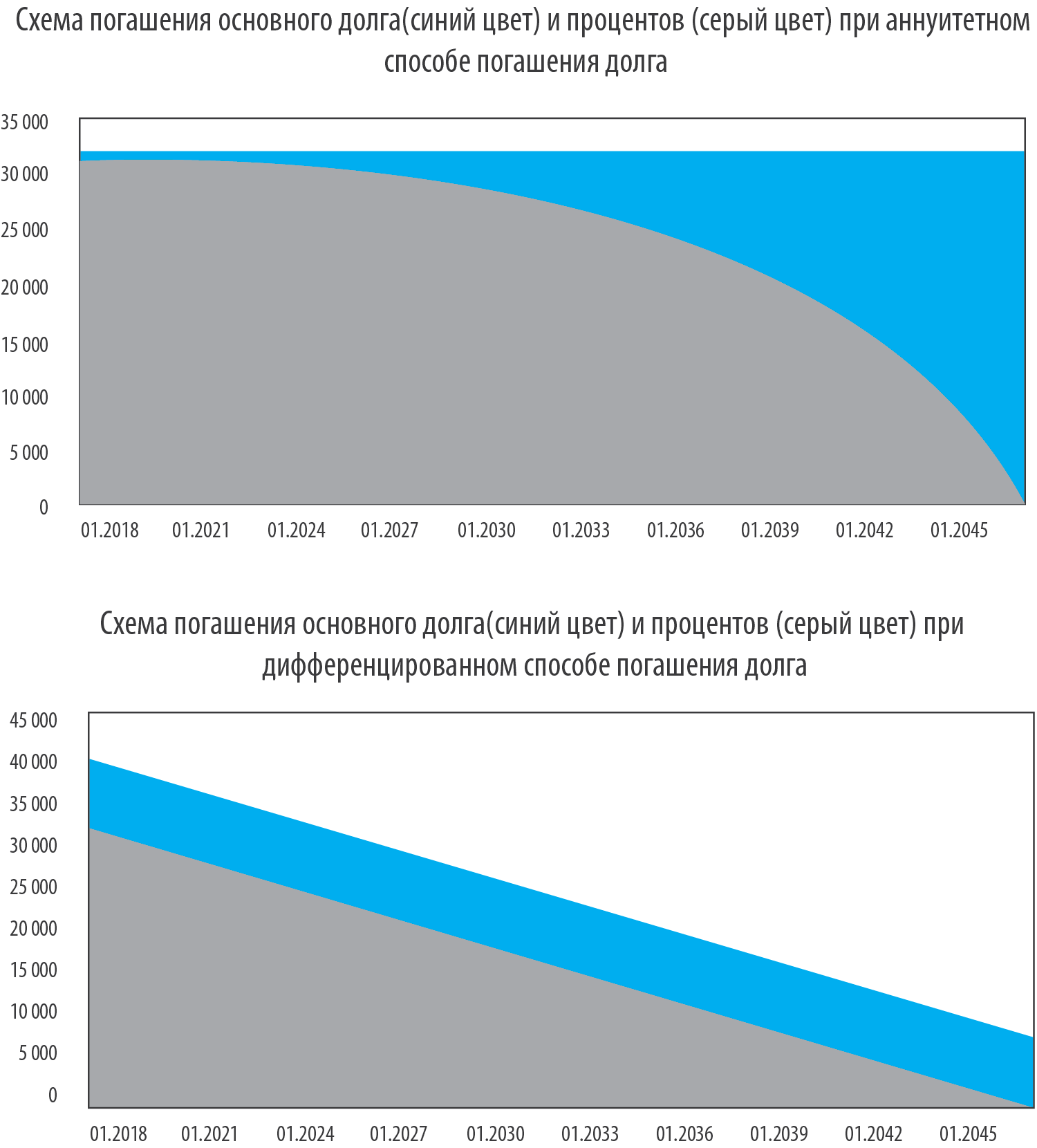 Зато при аннуитетной схеме погашения банк вам даст кредит на большую сумму, чем при дифференцированной. Кроме того, некоторые банки, предлагающие дифференцированную схему погашения платежей, «защищаются» от досрочного погашения кредита. Устанавливают для досрочного платежа дополнительные условия, например, о том, что досрочный взнос должен в 5 раз превышать ежемесячный.
Зато при аннуитетной схеме погашения банк вам даст кредит на большую сумму, чем при дифференцированной. Кроме того, некоторые банки, предлагающие дифференцированную схему погашения платежей, «защищаются» от досрочного погашения кредита. Устанавливают для досрочного платежа дополнительные условия, например, о том, что досрочный взнос должен в 5 раз превышать ежемесячный.
Оценивая схемы погашения, мы должны учитывать самые различные факторы, которые в итоге приведут к выбору наиболее выгодных условий кредитования. Однако мы понимаем, что заёмщику выгоднее платить кредит дифференцированными платежами, а банку — выдавать кредит аннуитетом, так как проценты при выдаче кредита при аннуитетных платежах начисляются по более выгодной для банка схеме.
Журова Анна Леонидовна, Карпущенко Наталья Петровна — консультанты-методисты по финансовой грамотности.
InfoBank.
 by | Аналитика | Способы погашения кредита. Какой лучше ?
by | Аналитика | Способы погашения кредита. Какой лучше ?
Способы погашения кредита. Какой лучше ? |
|
Должо-о-ок… |
Сегодня мы поговорим о такой сложной материи, как кредиты на недвижимость и способы их погашения. Точнее говоря, именно на способах погашения и вопросе — почему в них важно разобраться — мы и остановимся.
Рынок предоставляемых банками кредитов на недвижимость, безусловно, разнообразен. На этапе заключения кредитного договора с банком нелишне будет блеснуть интеллектом и полюбопытствовать, а какой способ погашения кредитной задолженности используется: в зависимости от фактического остатка или по аннуитету?
Итак, все способы погашения кредитов на недвижимость можно условно разбить на две группы
A — Аннуитет (погашение равными частями в течение срока кредитования).

В основе любого математического действия лежит формула. Вычитание денежных средств из Вашего кошелька в данном случае производится по следующим правилам: общая сумма кредитной задолженности и проценты по ней делятся равными частями на количество периодов погашения.
Проценты к погашению при этом рассчитываются по следующей формуле:
С – сумма кредита ПС – процентная ставка по кредиту ПП – количество месяцев пользования кредитом ПМ –количество платежных месяцев (может отличаться от количества месяцев пользования кредитом, например, при 3-х месячной отсрочке платежа по процентам) |
Например, имеются следующие исходные данные: сумма кредита – 60 тыс.
 долларов США, срок кредитования – 15 лет, ставка по кредиту – 14% годовых.
долларов США, срок кредитования – 15 лет, ставка по кредиту – 14% годовых. Рассчитываем сумму процентов
60 000 : 12 х 0,14 х (180 + 1) :2 : 177 (при условии вышеуказанной отсрочки платежа по процентам в 3 месяца, т.е. 180 – 3= 177) Итак, получилась сумма 357, 9 долларов США.
Основной долг 60 000 : 180= 333, 3 долларов США
Общая сумма 357,9 +333,3= 691,2 долларов США
Данная сумма будет постоянна на протяжении всего периода погашения кредита.
Умножьте эту сумму на количество месяцев — в результате по такой схеме за 15 лет вы выплатите банку 123,4 тыс.долларов США.
По такой формуле считаются льготные кредиты на жилье. Последние, в основном, выдаются в ОАО «АСБ Беларусбанк» (и некоторых других государственных банках).
Выплату по аннуитету в кредитах выданных на общих основаниях смотрите в таблице
B— Погашение кредита в зависимости от фактического остатка кредитной задолженности.
В данном случае, как ясно из названия, долг по кредиту погашается равными долями, а проценты — в зависимости от того, какая сумма основного долга по кредиту осталась к погашению в данном месяце.
Формула при этом используется следующая:
|
Где П – сумма процентов в данном месяце С – сумма кредита ПС – процентная ставка по кредиту |
Сумма процентов, которые нужно будет выплатить в первом месяце после получения кредита, когда долг по кредиту «висит» в полном объеме: 60 000 х 0,14 :12= 700 долларов США
Часть основного долга к погашению 60 000 : 180 =333,3 доллара США
Общая сумма к погашению в первом месяце равна 1033,3 доллара США.
Однако эта сумма будет постепенно уменьшаться. Но значительное уменьшение начнется не ранее чем через половину срока, т.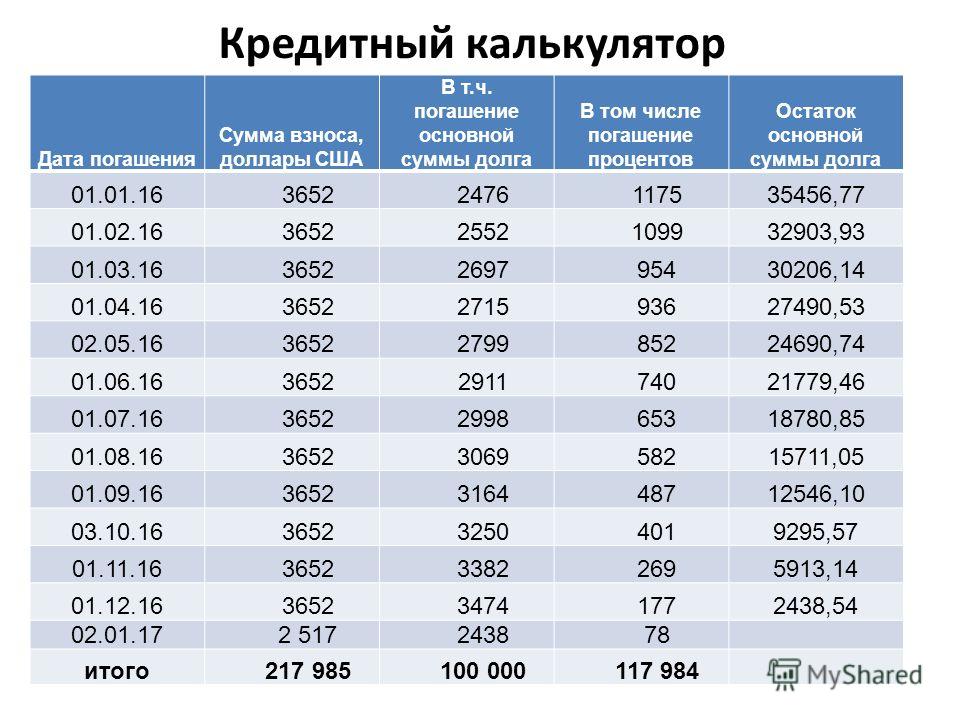 е семь с половиной лет. Только тогда размер ежемесячного платежа по кредиту станет примерно равным 691 доллару США, то есть рассмотренному в первом случае.
е семь с половиной лет. Только тогда размер ежемесячного платежа по кредиту станет примерно равным 691 доллару США, то есть рассмотренному в первом случае.
При таком варианте погашения за весь срок кредитования вы выплатите банку 123,35 тыс.долларов США.
Теперь рассмотрим основные отличительные особенности этих двух вариантов погашения кредита.
| ||||||||||||||
В настоящее время доля кредитов с аннуитетными платежами в общем объеме выдаваемых кредитов на недвижимость довольно незначительна.
 Оно и понятно, мало того, что мировой финансовый кризис уже сказался на объемах кредитования белорусских банков, так еще и возврат причитающихся процентов по кредитам растягивается по времени почти в два раза, по сравнению с использованием обычных схем кредитования.
Оно и понятно, мало того, что мировой финансовый кризис уже сказался на объемах кредитования белорусских банков, так еще и возврат причитающихся процентов по кредитам растягивается по времени почти в два раза, по сравнению с использованием обычных схем кредитования.Поэтому, если уж отыскали данный кредит, будьте бдительны: путем математических расчетов мы определили, что в итоге сумма платежей по аннуитету значительно превысит процентные платежи по фактическому остатку.
Возьмем, к примеру, несколько белорусских банков и посмотрим, какие схемы используют они:
Конечно, список продолжать можно еще долго. Это лишь часть того, что предлагается на сегодняшнем рынке банковских услуг. В каждом конкретном случае необходимо по возможности получать детальную консультацию по кредиту с тем, чтобы избежать возможных осложнений.
Как говорится, кто предупрежден – тот вооружен….

Марина Пантелеенко специально для www.infobank.by
финансовых формул (с калькуляторами)
Люди из всех слоев общества, от студентов, биржевых маклеров и банкиров; риэлторам, домовладельцам и управляющим находят финансовые формулы невероятно полезными в повседневной жизни. Используете ли вы финансовые формулы для личных или по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь.
Независимо от того, в какой сфере финансов вы работаете или учитесь, от корпоративных финансов до банковского дела, все они построены на тот же фундамент стандартных формул и уравнений.Хотя некоторые из этих сложных формул могут сбить с толку обычного человека, мы помочь, внося вам ясность.
Имеете ли вы дело со сложными процентами, аннуитетами, акциями или облигациями, инвесторы должны иметь возможность эффективно оценивать
уровень ценности или достоинства их финансовых показателей. Это делается путем оценки будущей прибыли и ее расчета относительно
текущая стоимость или эквивалентная норма прибыли.
Это делается путем оценки будущей прибыли и ее расчета относительно
текущая стоимость или эквивалентная норма прибыли.
Финансовые формулы.net может помочь.
Финансовая информация и калькуляторы на сайте FinanceFormulas.net предназначены не только для профессионалов, но и для всех, кто потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа которые изучают финансы и бизнес, для профессионалов в области корпоративных финансов, FinanceFormulas.net поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха.
Кто может получить больше всего от FinanceFormulas.net?
Студенты, изучающие финансы и бизнес , могут использовать формулы и
калькуляторы, бесплатно предоставляемые FinanceFormulas.net в качестве постоянного справочника, во время учебы в школе, затем во время работы в
мир финансов.
Люди, уже работающие в сфере бизнеса , которые могут иметь Если вы забыли, как использовать конкретную формулу или набор уравнений, наши инструменты станут бесценным ресурсом.FinanceFormulas.net не только упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы больше никогда не придется тратить время на поиск нужного инструмента.
Любой . Люди любого возраста могут пользоваться калькуляторами в FinanceFormulas.net, чтобы помочь им справляться с финансовыми трудностями повседневной жизни. Ипотека, задолженность по кредитной карте или понимание академической оценки вашего инвестиции, такие как акции и облигации, он имеет доступ к правильным формулам, уравнениям и калькуляторам, которые могут помочь вам проложите свой путь к финансово благополучной жизни.
Планируете ли вы использовать бесплатные формулы, предоставляемые FinanceFormulas. net, для личного или академического использования,
FinanceFormulas.net здесь, чтобы помочь вам найти банковские формулы, формулы акций и облигаций, корпоративные и прочие
формулы, которые вам нужны.
net, для личного или академического использования,
FinanceFormulas.net здесь, чтобы помочь вам найти банковские формулы, формулы акций и облигаций, корпоративные и прочие
формулы, которые вам нужны.
Вернуться к началу
Расчет настоящей и будущей стоимости аннуитетов
У большинства из нас был опыт совершения серии фиксированных платежей в течение определенного периода времени, таких как аренда или оплата автомобиля, или получение серии платежей в течение определенного периода времени, таких как проценты по облигации или депозитному сертификату ( CD).Эти повторяющиеся или текущие платежи технически называются «аннуитетами» (не путать с финансовым продуктом, называемым аннуитетом, хотя они взаимосвязаны).
Есть несколько способов измерить стоимость таких платежей или их конечную стоимость. Вот что вам нужно знать о расчете текущей стоимости (PV) или будущей стоимости (FV) аннуитета.
Ключевые выводы
- Периодические платежи, такие как арендная плата за квартиру или проценты по облигациям, иногда называют «аннуитетами».
 «
« - При обычных аннуитетах выплаты производятся в конце каждого периода. При уплате аннуитетов они производятся в начале периода.
- Будущая стоимость аннуитета — это общая сумма выплат в определенный момент. со временем
- Текущая стоимость — это то, сколько денег потребовалось бы сейчас, чтобы произвести эти будущие платежи.
Два типа аннуитета
Аннуитеты в этом смысле слова делятся на два основных типа: обычные аннуитеты и аннуитеты, подлежащие уплате.
- Обычные аннуитеты : Обычные аннуитеты производят (или требуют) выплаты в конце каждого периода. Например, по облигациям проценты обычно выплачиваются в конце каждые шесть месяцев.
- Аннуитеты к уплате : Напротив, при уплате аннуитета выплаты производятся в начале каждого периода. Арендная плата, которую арендодатели обычно требуют в начале каждого месяца, является типичным примером.
Вы можете рассчитать настоящую или будущую стоимость обычной или причитающейся ренты, используя следующие формулы.
Расчет будущей стоимости обычной ренты
Будущая стоимость (FV) — это мера того, сколько будет стоить серия регулярных платежей в определенный момент в будущем при определенной процентной ставке. Так, например, если вы планируете инвестировать определенную сумму каждый месяц или год, он сообщит вам, сколько вы накопите на будущую дату. Если вы производите регулярные выплаты по ссуде, будущая стоимость полезна для определения общей стоимости ссуды.
Рассмотрим, например, серию из пяти регулярных платежей по 1000 долларов.
Изображение Джули Банг © Investopedia 2019 Из-за временной стоимости денег — концепции, согласно которой любая данная сумма сейчас стоит больше, чем она будет в будущем, потому что она может быть инвестирована тем временем, — первый платеж в 1000 долларов стоит больше, чем второй, и так далее. Итак, предположим, что вы инвестируете 1000 долларов каждый год в течение следующих пяти лет под 5% годовых. Ниже показано, сколько у вас будет в конце пятилетнего периода.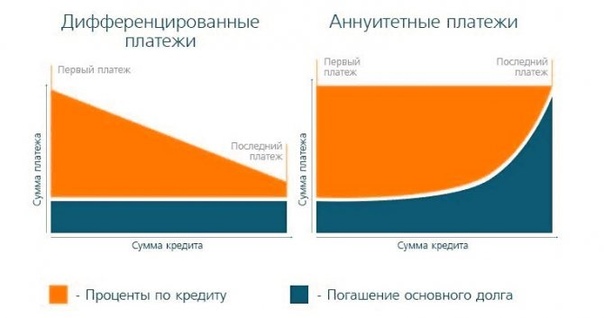 n — 1} {i} \ right] \\ & \ textbf {где:} \\ & \ text {C} = \ text {денежный поток за период} \\ & i = \ text {процентная ставка} \\ & n = \ text {количество платежей} \\ \ end {выровнено} FVОбычный аннуитет = C × [i (1 + i) n − 1], где: C = денежный поток за период i = процентная ставка = количество платежей
n — 1} {i} \ right] \\ & \ textbf {где:} \\ & \ text {C} = \ text {денежный поток за период} \\ & i = \ text {процентная ставка} \\ & n = \ text {количество платежей} \\ \ end {выровнено} FVОбычный аннуитет = C × [i (1 + i) n − 1], где: C = денежный поток за период i = процентная ставка = количество платежей
Используя приведенный выше пример, вот как это будет работать:
FVОбычный аннуитет = 1000 долларов США × [(1 + 0.5 -1} {0,05} \ right] \\ & = \ 1000 долларов \ times 5,53 \\ & = \ 5 525,63 долларов \\ \ end {выровнено} FVОбычная рента = 1000 долларов × [0,05 (1 + 0,05) 5−1 ] = 1000 долларов США × 5,53 = 5 525,63 долларов США
Обратите внимание, что разница в один цент в этих результатах — 5 525,64 доллара против 5 525,63 доллара — связана с округлением в первом расчете.
Расчет текущей стоимости обычной ренты
В отличие от расчета будущей стоимости, расчет приведенной стоимости (PV) показывает, сколько денег потребуется сейчас, чтобы произвести серию платежей в будущем, опять же с учетом установленной процентной ставки. {-n}} {i} \ right] \\ \ end {выровненный} PV Обычный ренту = C × [i1− (1 + i) −n]
{-n}} {i} \ right] \\ \ end {выровненный} PV Обычный ренту = C × [i1− (1 + i) −n]
Если мы подставим те же числа, что и выше, в уравнение, вот результат:
PVОбычный аннуитет = 1000 долларов США × [1− (1 + 0.{-5}} {0,05} \ right] \\ & = \ 1000 долларов \ times 4,33 \\ & = \ 4 329,48 долларов \\ \ end {выровнено} PV Обычная рента = 1 000 долларов × [0,051− (1 + 0,05) −5 ] = 1000 долларов США × 4,33 = 4329,48 долларов США
Расчет будущей стоимости подлежащей выплате ренты
Выплата аннуитета, как вы помните, отличается от обычной аннуитета тем, что выплаты по причитающейся аннуитету производятся в начале, а не в конце каждого периода.
Изображение Джули Банг © Investopedia 2019Для учета платежей, происходящих в начале каждого периода, требуется небольшая модификация формулы, используемой для расчета будущей стоимости обычного аннуитета, что приводит к более высоким значениям, как показано ниже.
Изображение Джули Банг © Investopedia 2019 Причина, по которой значения выше, заключается в том, что платежи, произведенные в начале периода, имеют больше времени для получения процентов.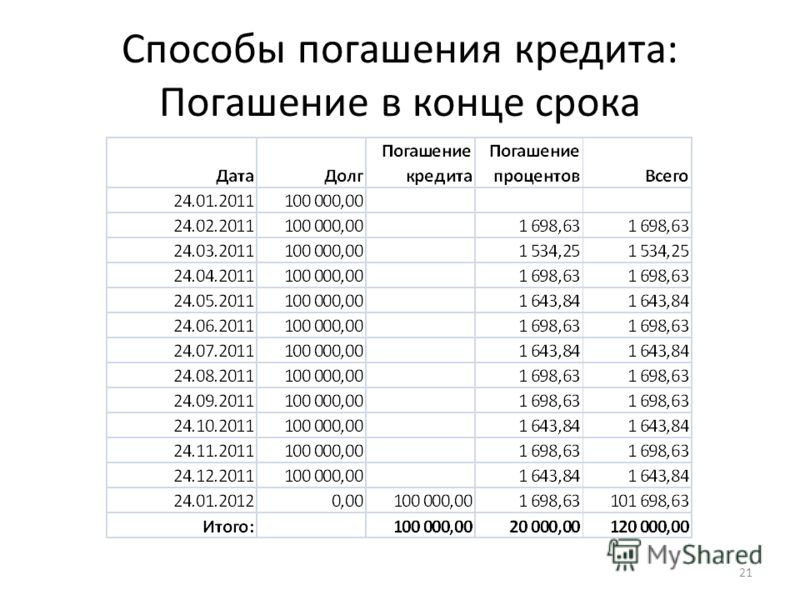 n — 1} {i} \ right] \ times (1 + i) \\ \ end {align} FVAnnuity Due = C × [i (1 + i) n − 1] × (1 + i)
n — 1} {i} \ right] \ times (1 + i) \\ \ end {align} FVAnnuity Due = C × [i (1 + i) n − 1] × (1 + i)
Здесь мы используем те же числа, что и в наших предыдущих примерах:
FVAnnuity Due = 1000 долларов США × [(1 + 0.5–1} {0,05} \ right] \ times (1 + 0,05) \\ & = \ 1000 долларов США \ times 5,53 \ times 1,05 \\ & = \ 5 801,91 доллара США \\ \ end {align} FVAnnuity Due = 1 000 долларов США × [ 0,05 (1 + 0,05) 5−1] × (1 + 0,05) = 1000 долларов США × 5,53 × 1,05 = 5 801,91 доллара США
Опять же, обратите внимание, что разница в один цент в этих результатах, 5 801,92 доллара против 5 801,91 доллара, связана с округлением в первом расчете.
Расчет приведенной стоимости аннуитета
Точно так же формула для расчета текущей стоимости причитающегося аннуитета учитывает тот факт, что выплаты производятся в начале, а не в конце каждого периода.
Например, вы можете использовать эту формулу для расчета приведенной стоимости ваших будущих арендных платежей, как указано в вашем договоре аренды. {-n}} {i} \ right] \ times (1 + i) \\ \ end {выровнено} PVAnnuity Due = C × [i1− (1 + i) −n] × (1 + i)
{-n}} {i} \ right] \ times (1 + i) \\ \ end {выровнено} PVAnnuity Due = C × [i1− (1 + i) −n] × (1 + i)
Итак, в этом примере:
PVAnnuity Due = 1000 долларов США × [(1− (1 + 0.{-5}} {0,05} \ right] \ times (1 + 0,05) \\ & = \ 1000 $ \ times 4.33 \ times1.05 \\ & = \ 4545.95 $ \\ \ end {align} PVAnnuity Due = 1000 долларов США × [0,05 (1– (1 + 0,05) −5] × (1 + 0,05) = 1000 долларов США × 4,33 × 1,05 = 4545,95 долларов США
Текущая стоимость аннуитета
Итог
Формулы, описанные выше, позволяют — и относительно легко, если вы не возражаете против математики — определить настоящую или будущую стоимость либо обычной ренты, либо подлежащей выплате ренты. Финансовые калькуляторы (вы можете найти их в Интернете) также могут рассчитать их за вас с правильными данными.
Определение обычного аннуитета
Что такое обыкновенная рента?
Обычный аннуитет — это серия равных платежей, производимых в конце последовательных периодов в течение фиксированного периода времени.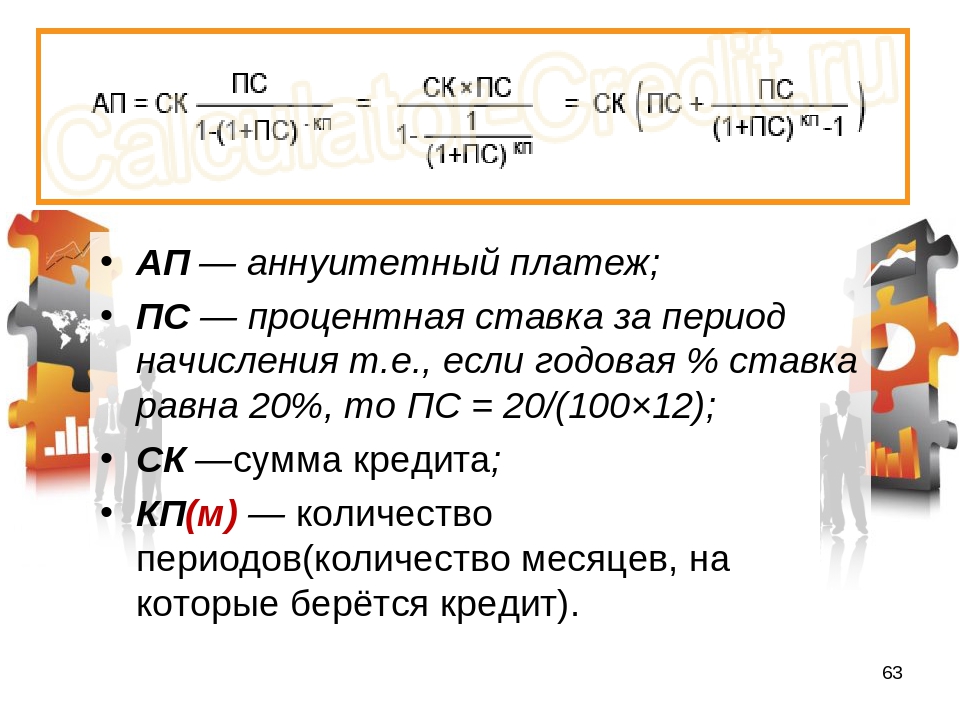 Хотя выплаты в рамках обычного аннуитета могут производиться так часто, как еженедельно, на практике они обычно производятся ежемесячно, ежеквартально, раз в полгода или ежегодно. Противоположностью обычной аннуитета является аннуитет, при котором выплаты производятся в начале каждого периода.Эти две серии платежей не то же самое, что финансовый продукт, известный как аннуитет, хотя они связаны.
Хотя выплаты в рамках обычного аннуитета могут производиться так часто, как еженедельно, на практике они обычно производятся ежемесячно, ежеквартально, раз в полгода или ежегодно. Противоположностью обычной аннуитета является аннуитет, при котором выплаты производятся в начале каждого периода.Эти две серии платежей не то же самое, что финансовый продукт, известный как аннуитет, хотя они связаны.
Ключевые выводы
- Обычный аннуитет — это серия регулярных платежей, производимых в конце каждого периода, например, ежемесячно или ежеквартально.
- В случае аннуитета, напротив, выплаты производятся в начале каждого периода.
- Последовательные ежеквартальные дивиденды по акциям являются одним из примеров обычной ренты; ежемесячная арендная плата является примером подлежащей уплате ренты.
Что такое обычная рента?
Как работает обычная рента
Примерами обычных аннуитетов являются выплаты процентов по облигациям, которые обычно выплачиваются раз в полгода, и ежеквартальные дивиденды по акциям, которые годами поддерживают стабильный уровень выплат. -n) / r)
-n) / r)
Например, если обычный аннуитет выплачивает 50 000 долларов в год в течение пяти лет, а процентная ставка составляет 7%, приведенная стоимость будет:
- Текущая стоимость = 50 000 долларов x ((1 — (1 + 0.-5) / 0,07) = 205 010 долл. США
Обычный аннуитет будет иметь более низкую приведенную стоимость, чем аннуитет, при прочих равных.
Текущая стоимость аннуитета Пример
Напомним, что при обычном аннуитете инвестор получает платеж в конце периода времени. Это контрастирует с аннуитетом, при котором инвестор получает платеж в начале периода. Типичным примером является квартплата, когда арендатор обычно платит арендодателю заранее за месяц вперед.- (5-1) / 0,07) = 219360 долларов США.
При прочих равных условиях аннуитет всегда стоит больше, чем обычный аннуитет, потому что деньги получены раньше.
Погашение кредита — обзор
§12.5.3 График погашения
Погашение кредита обычно начинается примерно через 6 месяцев после завершения строительства проекта, 16 и обычно производится с 6-месячным интервалом. В случае использования облигационного финансирования может быть создан фонд погашения для погашения всей суммы облигации при ее окончательном сроке погашения, а не выплаты в рассрочку, но это, очевидно, увеличивает стоимость финансирования и не является обычным явлением для облигаций проектного финансирования рынок.Следовательно, облигации проектного финансирования обычно амортизируются (погашаются) аналогично займам.
В случае использования облигационного финансирования может быть создан фонд погашения для погашения всей суммы облигации при ее окончательном сроке погашения, а не выплаты в рассрочку, но это, очевидно, увеличивает стоимость финансирования и не является обычным явлением для облигаций проектного финансирования рынок.Следовательно, облигации проектного финансирования обычно амортизируются (погашаются) аналогично займам.
Что касается структуры погашения, можно было бы подумать, что самый справедливый способ работы с кредиторами, предполагая, что денежный поток проекта будет разумно равномерным во времени ( cf . §7.3.2), — это погашение финансирования равными рассрочка ( например, , если долг составляет 1000, и он погашается в течение 10 лет, выплаты будут составлять 100 в год На самом деле, такая структура погашения, хотя и не редкость, но невыгодна для инвесторов проектной компании, поскольку большая часть денежного потока выплачивается кредиторам в первые годы ссуды, поскольку процентные платежи на этом этапе относительно высоки. Это также оставляет проект с более низкими ADSCR в первые годы, как раз в то время, когда на денежный поток проекта с большей вероятностью повлияют проблемы запуска. Таким образом, стандартный подход заключается в использовании структуры аннуитетных выплат, при которой сохраняется уровень основной суммы и процентных платежей на протяжении всего срока кредита.
Это также оставляет проект с более низкими ADSCR в первые годы, как раз в то время, когда на денежный поток проекта с большей вероятностью повлияют проблемы запуска. Таким образом, стандартный подход заключается в использовании структуры аннуитетных выплат, при которой сохраняется уровень основной суммы и процентных платежей на протяжении всего срока кредита.
Это можно проиллюстрировать упрощенными примерами в таблицах 12.5 и 12.6, которые имеют следующие общие допущения:
Таблица 12.5. Эффект от выплат основного долга
| Год: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | (a) Денежный поток проекта | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |||||||||||||||||||
| (на конец 2 года) 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 | 0 9026 9 | ||||||||||||||||||
| (г) Выплата процентов | 100 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | Обслуживание долга 9023 [(b) + (d)] | 200 | 190 | 180 | 170 | 160 | 150 | 140 | 130 | 120 | 110 | |||||||
| ADSC (e)] | 1. 10 10 | 1,16 | 1,22 | 1,29 | 1,38 | 1,47 | 1,57 | 1,69 | | 1,69 | | 1,69 | | Среднее значение ADSCR | 1,47 | 1,51 | 1,56 | 1,60 | 1,66 | 1.71 | 1,77 | 1,84 | 1,92 | | |||||
| LLCR [ЧПС ((а) ÷ (с))] | 1,35 | 1,41 ,14 | 1,53 | 1,60 | 1,67 | 1,74 | 1,82 | 1,91 | 2,00 | 2,00 | лет | |||||||||||||||||
| Точка зрения инвесторов | ||||||||||||||||||||||||||||
| Инвестиции в акционерный капитал: | 250 | д)] | 20 | 30 | 40 | 50 | 60 | 70 | 9 0268 8090 | 100 | 110 | |||||||||||||||||
| NPV инвестиций | 66 | |||||||||||||||||||||||||||
| IRR 6% | ||||||||||||||||||||||||||||
| MIRR капитала | 14,6% | 6 лет | ||||||||||||||||||||||||||
Таблица 12. 6. Эффект от аннуитетных выплат
6. Эффект от аннуитетных выплат
| Год: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9 | 9 | 9 (а) Денежный поток по проекту | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | 220 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 902 Точка зрения кредиторов 902 ) погашение кредита | 63 | 69 | 76 | 84 | 92 | 101 | 111 | 122 | 134 | 148 | |||||||||||||||||||||
| 902 (на конец года) 1000 Кредит | 937 | 868 | 792 | 709 | 617 | 516 | 405 | 282 | 148 | 0 | (d) Выплата процентов | 100 | 94 | 87 | 79 | 71 | 62 | 52 | 40 | 28 | 15 | ||||||||||
| Всего обслуживание долга (е) | б) + (г)] | 163 | 163 | 163 | 163 | 163 | 163 | 163 | 163 | 163 | 163 | 1. 35 35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | | Среднее значение ADSCR | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1.35 | 1,35 | 1,35 | 1,35 | LLCR [NPV ((а) ÷ (c))] | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | 1,35 | лет | |
| Точка зрения инвесторов | |||||||||||||||||||||||||||||||
| Инвестиции в акционерный капитал: | 250 | д)] | 57 | 57 | 57 | 57 | 57 | 57 | 9 0268 5757 | 57 | 57 | ||||||||||||||||||||
| ЧПС инвестиций | 74 | ||||||||||||||||||||||||||||||
| IRR698% | |||||||||||||||||||||||||||||||
| MIRR капитала | 14.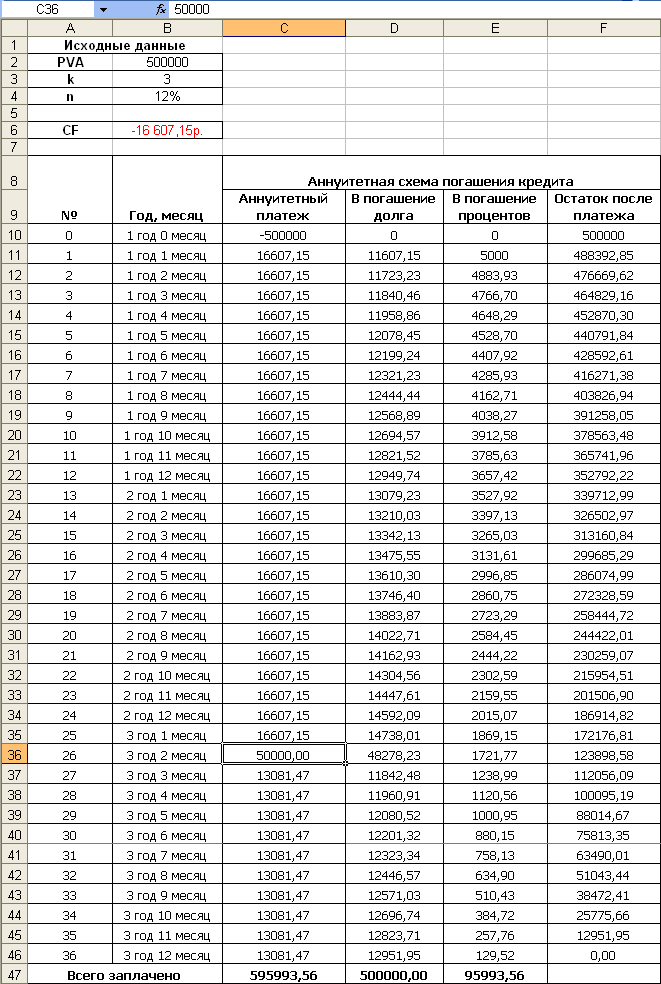 9% 9% | ||||||||||||||||||||||||||||||
- ●
Стоимость проекта: 1250;
- ●
соотношение заемный капитал: собственный капитал: 80:20;
- ●
сумма кредита: 1000;
- ●
погашение: 10 лет, ежегодно с просрочкой;
- ●
процентная ставка: 10% п.а. ;
- ●
сумма собственного капитала: 250;
- ●
Денежный поток до обслуживания долга и выплаты дивидендов: 220 в год. ;
- ●
денежный поток после обслуживания долга выплачен инвесторам;
- ●
остаточная стоимость проекта: ноль;
- ●
ставка дисконтирования NPV (стоимость капитала) инвесторов: 12%;
- ●
ставка реинвестирования инвесторов (для расчета MIRR): 12% р.
 а. ;
а. ;- ●
расчет игнорирует любой период строительства.
Непосредственная и очевидная проблема с уровнем основной структуры платежей заключается в том, что годовое обслуживание долга в год 1 (200) почти вдвое больше, чем в год 10 (110), и, соответственно, ADSCR составляет 1,10: 1 (слишком мало для комфорт) в 1-м году и 2,00: 1 (намного больше, чем необходимо) в 10-м году.
Инвесторские распределения, с другой стороны, в значительной степени являются отсроченными, при этом дивиденды увеличиваются в 5½ раз в период с 1 по 10 год; на то, чтобы окупить первоначальные вложения, уходит почти 6 лет.
Выгоды от перехода на аннуитетную структуру погашения очевидны: ADSCR составляет комфортную ставку 1,35: 1 во всем, благодаря равным платежам по обслуживанию долга, как и LLCR.
Дивиденды также одинаковы во всем, и хотя общие дивиденды, полученные инвесторами в течение срока реализации проекта, уменьшаются с 650 до 573 (поскольку кредиторам выплачивается больше процентов), IRR инвесторов улучшается с 16,6% до 18,8%. ; однако улучшение MIRR (более справедливое отражение изображения) более ограничено, начиная с 14.От 6% до 14,9%. Срок окупаемости существенно сокращается — до 4½ лет.
; однако улучшение MIRR (более справедливое отражение изображения) более ограничено, начиная с 14.От 6% до 14,9%. Срок окупаемости существенно сокращается — до 4½ лет.
Структура выплат относительно более важна для инвесторов, чем процентная ставка по долгу. Если в этом примере кредиторы предложили снизить свою процентную ставку на 0,25% в обмен на структуру выплаты основной суммы долга вместо аннуитета, прибыль от этого для инвесторов составит 0,6% годовых. , тогда как в аннуитетно-возвратной структуре стоит дополнительно 2,2% р.а. Аналогичным образом, вероятно, будет стоить платить более высокую процентную ставку для получения более долгосрочного финансирования, если для этого имеется достаточный «хвост» денежного потока.
Однако структура погашения аннуитета значительно увеличивает выплаты по обслуживанию долга и, таким образом, снижает ADSCR в более поздние годы реализации проекта. Это также увеличивает средний срок жизни долга: в таблице 12.5 он составляет 5½ лет, тогда как в таблице 12. 6 он составляет чуть более 6 over лет.
6 он составляет чуть более 6 over лет.
Если существует большая неопределенность относительно будущих денежных потоков от проекта, кредиторы могут искать более высокие коэффициенты покрытия и более короткий средний срок жизни, чем может быть достигнуто с помощью аннуитета.В таких случаях может потребоваться согласование компромисса между выплатами основного долга и аннуитетными выплатами.
С другой стороны, если проект, по прогнозам, принесет более высокие денежные потоки в последующие годы, график погашения с частичными выплатами по кредиту будет даже медленнее, чем при аннуитетной структуре, но с адекватными годовыми коэффициентами покрытия, хотя кредиторы сопротивляются слишком большая отсрочка погашения и, следовательно, чрезмерно долгий средний срок их погашения.
Если прогнозируются нерегулярные денежные потоки, выплаты по ссуде также могут быть структурированы по нерегулярному графику, чтобы на протяжении всего срока ссуды поддерживался один и тот же уровень ADSCR (это известно как «скульптурный» график погашения). Это может быть необходимо, например, если есть большие затраты на техническое обслуживание в течение одного года или если денежные потоки после уплаты налогов в последующие годы уменьшаются, потому что отсроченные налоги начинают подлежать уплате, если проектная компания получила выгоду от ускоренной налоговой амортизации своих активов в в первые годы работы, предполагая, что эти «всплески» не сглаживаются авансовыми платежами на резервных счетах ( ср. . §14.4.1).
Это может быть необходимо, например, если есть большие затраты на техническое обслуживание в течение одного года или если денежные потоки после уплаты налогов в последующие годы уменьшаются, потому что отсроченные налоги начинают подлежать уплате, если проектная компания получила выгоду от ускоренной налоговой амортизации своих активов в в первые годы работы, предполагая, что эти «всплески» не сглаживаются авансовыми платежами на резервных счетах ( ср. . §14.4.1).
Эти соображения имеют отношение не только к инвесторам: структура погашения долга явно влияет на стоимость продуктов или услуг проектной компании и может быть решающим фактором, если спонсоры участвуют в конкурентных торгах по перспективному проекту.
Временная стоимость денег — Совет по уравнению
В этом уроке обсуждается периодическое погашение ( PR ), одна из шести функций сложных процентов.
представлены в Разделе 505 (AH 505) Справочника оценщика, формулах и таблицах . Урок:
Урок:
- Объясняет значение и цель функции,
- Обсуждает процесс погашения кредита,
- Предоставляет формулу для расчета коэффициентов PR и
- Содержит практические примеры применения коэффициента PR .
PR : Значение и цель
PR — это сумма платежа с периодической процентной ставкой i и количеством периодов n , в котором текущая стоимость платежей равна 1 доллару США, при условии, что платежи происходят в конце каждого периода.
PR также называют коэффициентом погашения кредита или коэффициентом выплаты кредита, поскольку этот коэффициент обеспечивает
сумма платежа на доллар суммы кредита для полностью амортизированной ссуды. Коэффициенты PR указаны в столбце 6 AH 505.
Коэффициенты PR указаны в столбце 6 AH 505.
PR можно рассматривать как «противоположность» PW $ 1 / P, которая обсуждалась в Уроке 6; математически PR и PW $ 1/ P Коэффициенты являются обратными, как показано ниже:
Концептуально коэффициент PW 1 доллар / P обеспечивает приведенную стоимость будущей серии периодических платежей в размере 1 доллара США, тогда как коэффициент PR обеспечивает равные периодические выплаты, текущая стоимость которых составляет 1 доллар.
Погашение кредита
Если ссуда погашается равными периодическими частями в течение срока ее действия, ссуда полностью амортизируется.
В случае полностью амортизированной ссуды каждый платеж представляет собой часть процентов и частичное погашение основной суммы долга. В течение срока полностью амортизированной ссуды основная сумма погашается полностью.
В течение срока полностью амортизированной ссуды основная сумма погашается полностью.
С точки зрения кредитора, заем — это вложение.В амортизированной ссуде часть платежа, которая представляет собой проценты, обеспечивает кредитору доход в размере на инвестиций, а часть платеж, который является погашением основной суммы долга, обеспечивает кредитору возврат из инвестиций.
График погашения показывает распределение платежей по ссуде между основной суммой и процентами по всему
весь срок кредита.Графики амортизации полезны, потому что погашение процентов и основной суммы может рассматриваться по-разному для
для целей подоходного налога, и необходимо вести учет отдельных сумм для каждого.
График погашения кредита ниже показывает график погашения 10-летнего кредита,
по годовой ставке 6%, с ежегодными выплатами.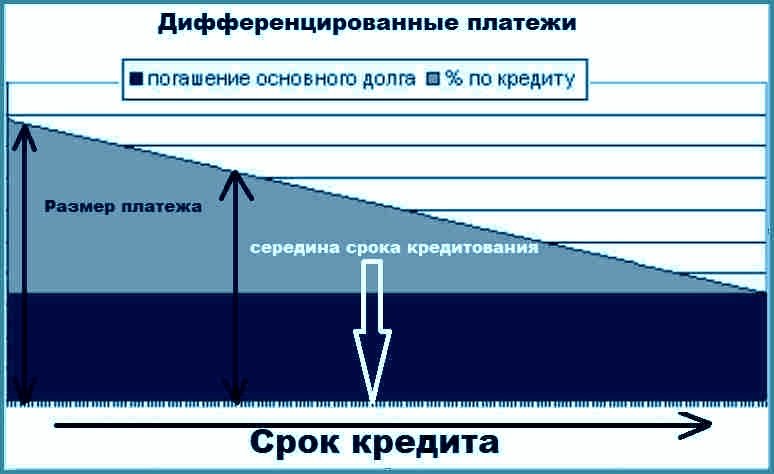
Формула для расчета
Факторы PRФормула для расчета коэффициентов PR :
Где:
- PR = коэффициент периодической выплаты
- i = Периодическая процентная ставка, часто выражаемая как годовая процентная ставка
- n = количество периодов, часто выражается в годах
Чтобы рассчитать коэффициент PR на 4 года при годовой процентной ставке 6%, используйте следующую формулу:
Просмотров на временной шкале:
На временной шкале четыре платежа отрицательны, потому что с точки зрения заемщика они будут оттоком денежных средств.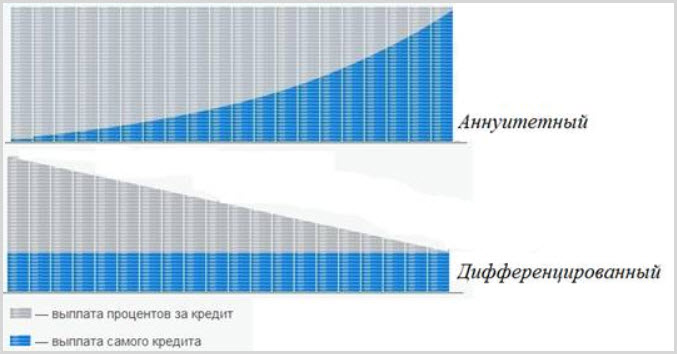 Сумма заимствования, 1 доллар, является положительной, поскольку с точки зрения заемщика это будет приток денежных средств.
Сумма заимствования, 1 доллар, является положительной, поскольку с точки зрения заемщика это будет приток денежных средств.
Чтобы найти коэффициент PR в AH 505, перейдите на страницу 33 AH 505. Спуститесь на 4 года и перейдите к столбцу 6. Коэффициент PR равен 0,288591.
Ссылка на AH 505, стр. 33
Практическое применение
PR Пример 1:
Вы только что взяли взаймы 50 000 долларов, которые будут выплачиваться равными ежегодными платежами в конце каждого из следующих 20 лет.Годовая процентная ставка — 8%. Какая сумма каждого годового платежа?
Решение:
- PMT = PV × PR (8%, 20 лет , годовых )
- PMT = 50 000 долларов США × 0,101852
- PMT = 5092 доллара.
 60
60
- Найдите годовой коэффициент PR (годовое начисление сложных процентов) для 8% на срок 20 лет. В AH 505, стр. 41, спуститесь на 20 лет и перейдите к столбцу 6, чтобы найти правильный коэффициент 0,101852.
- Ежегодный платеж в размере 5 092,60 долларов США — это сумма кредита в размере 50 000 долларов США, умноженная на коэффициент PR .
Ссылка на AH 505, стр. 41
Пример 2:
Вы берете взаймы 200000 долларов на покупку дома, используя полностью амортизируемую ипотеку с ежемесячными выплатами в течение 30 лет под 5% годовых.Какой у вас ежемесячный платеж в счет основного долга и процентов?
Решение:
- PMT = PV × PR (5%, 30 лет , годовой )
- PMT = 200 000 долларов США × 0,005368
- PMT = 1073 доллара.
 60
60
- Найдите ежемесячный коэффициент PR (ежемесячное начисление сложных процентов) для 5% при сроке действия 30 лет. В AH 505, стр. 28, спуститесь на 30 лет и перейдите к столбцу 6, чтобы найти правильный коэффициент 0,005368.
- Ежемесячный платеж в размере 1 073,60 долларов США равен сумме кредита, умноженной на ежемесячный коэффициент PR .
Ссылка на AH 505, стр. 28
Пример 3:
Джон берет взаймы 75 000 долларов под 6% годовых с выплатой равных ежегодных платежей в конце каждого из следующих 10 лет.Какая часть первого платежа Джона составляет основную сумму, а какая — проценты?
Решение:
- PMT = PV × PR (6%, 10 лет , годовой )
- PMT = 75 000 долларов США × 0,135868
- PMT = 10 190 долларов США
- Найдите годовой коэффициент PR (годовое начисление сложных процентов) для 6% при сроке действия 10 лет.
 В AH 505, стр. 33,
спуститесь на 10 лет и перейдите к столбцу 6, чтобы найти правильный коэффициент 0,135868.
В AH 505, стр. 33,
спуститесь на 10 лет и перейдите к столбцу 6, чтобы найти правильный коэффициент 0,135868. - Ежегодный платеж в размере 10 190 долларов — это сумма кредита, умноженная на годовой коэффициент PR . Выплата делится между выплатой процентов и основной суммы.
- Непогашенный остаток по кредиту за первый год составляет 75 000 долларов, поэтому сумма процентов за первый год — 75000 долларов × 0.06 = 4500 долларов.
- Сумма погашения основного долга составляет 10 190 долларов (годовой платеж) — 4500 долларов (сумма процентов) = 5 690 долларов.
Ссылка на AH 505, стр. 33
Пример 4:
У друга, который вот-вот собирается выйти на пенсию, на пенсионном счету 401 тысяч долларов есть 400 000 долларов. Если он сможет зарабатывать 4% годовых на счете
и желает исчерпать фонд в течение 20 лет с равным ежегодным снятием средств, сколько он может снимать в конце каждого года?
Если он сможет зарабатывать 4% годовых на счете
и желает исчерпать фонд в течение 20 лет с равным ежегодным снятием средств, сколько он может снимать в конце каждого года?
Решение:
- PMT = PV × PR (4%, 20 лет , годовой )
- PMT = 400 000 долларов США × 0.073582
- PMT = 29 433 долларов США
- Найдите годовой коэффициент PR (годовое начисление сложных процентов) для 4% при сроке действия 20 лет. В AH 505, стр.25, спуститесь на 20 лет и перейдите к столбцу 6, чтобы найти правильный коэффициент 0,073582.
- Ежегодный платеж в размере 29 433 долларов представляет собой сумму 400 000 долларов на пенсионном счете, умноженную на годовой коэффициент PR .

- Друг мог снимать 29 433 доллара в конце каждого года в течение 20 лет, предполагая, что он сможет заработать годовая ставка 4% от остатка на счете. Через 20 лет счет будет пуст.
Ссылка на AH 505, стр.25
Основное использование фактора PR заключается в предоставлении суммы периодического платежа, необходимого для погашения данной суммы кредита.Но вы также можете используйте его, чтобы указать размер периодического платежа, который будет поддерживать данная сумма, при условии годовой процентной ставки и срока, как в этом примере.
Пример 5:
Вы берете ипотечный кредит на сумму 100 000 долларов США под 6% годовых с ежемесячными выплатами в течение 30 лет. Вы планируете продать недвижимость через 12 лет.
В то время каков будет непогашенный остаток (т.е., остаток основного долга) по кредиту?
Вы планируете продать недвижимость через 12 лет.
В то время каков будет непогашенный остаток (т.е., остаток основного долга) по кредиту?
Решение:
Первым шагом является расчет суммы платежа:
- PMT = PV × PR (6%, 30 лет , ежемесячно )
- PMT = 100 000 долларов США × 0.005996
- PMT = 599,60 $
- Найдите ежемесячный коэффициент PR (ежемесячное начисление сложных процентов) для 6% при сроке действия 30 лет. В 505 г. хиджры, стр.32, спуститесь на 30 лет и
перейдите к столбцу 6, чтобы найти правильный месячный коэффициент 0,005996.

- Ежемесячный платеж в размере 599,60 долларов представляет собой сумму кредита в размере 100 000 долларов, умноженную на ежемесячный коэффициент PR .
Ссылка на AH 505, стр. 32
Остаток погашаемой ссуды представляет собой приведенную стоимость оставшихся платежей по ссуде, дисконтированных по ссуде. контрактная процентная ставка. Второй шаг — дисконтировать оставшиеся 18 лет ежемесячных платежей с использованием коэффициента PW $ 1/ P при 6%.
- PV = PMT × PW $ 1/ P (6%, 18 лет , ежемесячно )
- PV = 599 долларов США.60 × 131.897876
- ЛС = 79 085,97 долл. США
- Найдите ежемесячный коэффициент PW $ 1/ P (ежемесячное начисление сложных процентов) для 6% в течение 18 лет.
 В AH 505, страница 32, пройдите 18 лет вниз и перейдите к столбцу 5.
чтобы найти правильный ежемесячный коэффициент PW $ 1/ P , равный 131,897876.
В AH 505, страница 32, пройдите 18 лет вниз и перейдите к столбцу 5.
чтобы найти правильный ежемесячный коэффициент PW $ 1/ P , равный 131,897876. - Оставшийся остаток кредита в размере 79 085 долларов США.97 — это сумма платежа в размере 599,60 долларов, умноженная на коэффициент PW $ 1/ P .
Ссылка на AH 505, стр. 32
типов графиков выплат срочных кредитов | Разработчик решений Ag
Виды графиков выплаты срочных кредитов
Многие ссуды погашаются посредством серии платежей в течение определенного периода времени. Эти платежи обычно включают сумму процентов, рассчитанную на невыплаченный остаток ссуды, плюс часть невыплаченного остатка ссуды.Эта выплата части невыплаченного остатка ссуды называется выплатой основной суммы долга.
Обычно существует два типа графиков погашения ссуд — даже основные платежи и даже общие платежи.
Выплаты по четной основной сумме
При четном графике платежей по основному долгу размер основного платежа одинаков для всех платежей. Он рассчитывается путем деления суммы первоначальной ссуды на количество платежей. Например, ссуда в размере 10 000 долларов, показанная в таблице 1, разделена на 20 периодов выплат продолжительностью один год каждый, в результате чего основной платеж составляет 500 долларов за платеж по ссуде.Проценты начисляются на сумму невыплаченного остатка по кредиту в каждый платежный период. Поскольку невыплаченный остаток по кредиту уменьшается с каждым платежом по основной сумме, размер процентных платежей по каждому платежу по ссуде также уменьшается. Это приводит к уменьшению общего платежа (основная сумма плюс проценты), как показано на Рисунке 1. Как показано в Таблице 1, общий платеж уменьшается с 1200 долларов (500 долларов США по основной сумме и 700 долларов по процентам) в первый год до 535 долларов (500 долларов по основной сумме и 35 долларов по процентам) ) в год 20. Общая сумма, выплаченная за 20-летний период, составляет 17 350 долларов США, которая состоит из ссуды в размере 10 000 долларов США плюс 7350 долларов США процентов.
Общая сумма, выплаченная за 20-летний период, составляет 17 350 долларов США, которая состоит из ссуды в размере 10 000 долларов США плюс 7350 долларов США процентов.
Выплаты равной суммы
Четный общий график платежей состоит из убывающих процентных выплат и увеличивающихся выплат основной суммы. Уменьшение размера процентных платежей сопровождается увеличением размера основного платежа, так что размер общего платежа по ссуде остается неизменным в течение срока ссуды (Рисунок 2).Как показано в таблице 2, выплата процентов уменьшается по мере уменьшения невыплаченного остатка. Оставшаяся часть платежа по кредиту — это основной платеж.
Большой невыплаченный остаток в начале срока действия ссуды означает, что большую часть общей суммы платежа составляют проценты с небольшой выплатой основного долга. Поскольку в первые периоды выплаты основного долга невелики, невыплаченный остаток по ссуде медленно уменьшается. Однако по мере того, как платежи продвигаются в течение срока действия ссуды, невыплаченный остаток уменьшается, что приводит к меньшим процентным выплатам и позволяет выплачивать больший основной платеж.В свою очередь, более высокий основной платеж увеличивает скорость уменьшения невыплаченного баланса. Например, выплата процентов составляет 700 долларов, а основной платеж составляет 244 доллара в течение первого года, как показано в таблице 2. Выплата процентов составляет 62 доллара, а основная выплата составляет 882 доллара во время последнего платежа по ссуде в 20-м году. Это в отличие от четного платежа. график выплат основной суммы, при котором основной платеж является постоянным в течение периода погашения, а невыплаченный остаток уменьшается на ту же сумму каждый период (платеж в размере 500 долларов США), что приводит к фиксированному сокращению выплаты процентов в каждом периоде на 35 долларов США (7% x 500 долларов США = 35 долларов США) .Общая сумма, выплаченная за 20-летний период, составляет 18 879 долларов, что включает ссуду в размере 10 000 долларов плюс 8 879 долларов процентов.
Однако по мере того, как платежи продвигаются в течение срока действия ссуды, невыплаченный остаток уменьшается, что приводит к меньшим процентным выплатам и позволяет выплачивать больший основной платеж.В свою очередь, более высокий основной платеж увеличивает скорость уменьшения невыплаченного баланса. Например, выплата процентов составляет 700 долларов, а основной платеж составляет 244 доллара в течение первого года, как показано в таблице 2. Выплата процентов составляет 62 доллара, а основная выплата составляет 882 доллара во время последнего платежа по ссуде в 20-м году. Это в отличие от четного платежа. график выплат основной суммы, при котором основной платеж является постоянным в течение периода погашения, а невыплаченный остаток уменьшается на ту же сумму каждый период (платеж в размере 500 долларов США), что приводит к фиксированному сокращению выплаты процентов в каждом периоде на 35 долларов США (7% x 500 долларов США = 35 долларов США) .Общая сумма, выплаченная за 20-летний период, составляет 18 879 долларов, что включает ссуду в размере 10 000 долларов плюс 8 879 долларов процентов.
Неоплаченный остаток
Невыплаченный остаток по кредиту с использованием четного графика платежей по основной сумме уменьшается на фиксированную сумму с каждым платежом. Как показано в таблице 1, невыплаченный остаток уменьшается на 500 долларов каждый год. По истечении 10 лет (половина срока погашения) невыплаченный остаток ссуды составляет 5000 долларов (половина от первоначальной ссуды в 10000 долларов).Напротив, размер невыплаченного остатка по четному общему графику платежей медленно уменьшается в течение раннего срока ссуды (например, 244 доллара в первый год) и быстро уменьшается к концу срока ссуды (например, 822 доллара в год 20). Как показано в Таблице 2, невыплаченный остаток за 10-й год (в середине срока кредита) составляет 6 630 долларов. Более половины кредита еще не погашено. Эта разница в скорости уменьшения невыплаченного остатка по двум графикам погашения показана на Рисунке 3.
Поскольку невыплаченный остаток по ссуде с использованием графика погашения равных общих платежей снижается медленнее, чем график погашения четных платежей по основной сумме, общая сумма процентов, выплачиваемых за 20 лет, больше при равномерном общем графике платежей. Например, в таблицах 1 и 2 общая сумма процентов, выплачиваемых в течение срока ссуды, составляет 7350 долларов при использовании четного графика выплат основной суммы и 8 878 долларов при использовании четного общего графика выплат для увеличения на 1528 долларов.Соответственно, общая стоимость погашения кредита больше на такую же сумму при четном общем графике выплат.
Например, в таблицах 1 и 2 общая сумма процентов, выплачиваемых в течение срока ссуды, составляет 7350 долларов при использовании четного графика выплат основной суммы и 8 878 долларов при использовании четного общего графика выплат для увеличения на 1528 долларов.Соответственно, общая стоимость погашения кредита больше на такую же сумму при четном общем графике выплат.
Платежи по воздушным шарам
Ссуды Someterm включают выплату по размеру. При такой структуре остаток по кредиту подлежит погашению после того, как будет произведена часть годовых платежей. В таблице 3 показан четный общий график выплат с амортизацией (распределением) за сорок лет. Однако при десятом годовом платеже наступает срок погашения остатка кредита.Это разовый платеж в размере 10 058 долларов, который состоит из остатка по ссуде 9 400 долларов и 658 долларов годовых процентов, подлежащих уплате в десятый год, как показано в таблице.
Резерв может использоваться, когда бизнес имеет ограниченную способность погашения в первые годы, но может выплатить или рефинансировать ссуду после нескольких лет работы (в данном случае 10 лет). Продолжительность графика погашения и сроки выплаты баллов могут быть адаптированы к индивидуальной ситуации.Заем может погашаться в течение длительного периода времени (например, 40 лет в примере), чтобы в первые годы выплаты были небольшими. В некоторых случаях досрочные платежи могут быть не выплачены, а включены в общий платеж.
Продолжительность графика погашения и сроки выплаты баллов могут быть адаптированы к индивидуальной ситуации.Заем может погашаться в течение длительного периода времени (например, 40 лет в примере), чтобы в первые годы выплаты были небольшими. В некоторых случаях досрочные платежи могут быть не выплачены, а включены в общий платеж.
Расчет равных выплат по кредиту
Финансовый калькулятор или электронная таблица на персональном компьютере — полезный инструмент для расчета платежей по кредиту с использованием четного общего графика платежей.
- «ПС» представляет собой заемную сумму.
- «Ставка» или «i» представляет собой процентную ставку за период выплаты.
- «N» или «Nper» представляет количество периодов выплаты.
- «PMT» представляет собой платеж по кредиту за период платежа.
Вы можете вычислить любое из четырех вышеуказанных значений ссуды, если вам известны три других значения.
Вы можете рассчитать платеж по ссуде, если знаете сумму ссуды, процентную ставку и продолжительность ссуды (количество периодов выплат).Например, если вы занимаетесь 10 000 долларов под 7% на 20 лет, ваш годовой платеж составит 943,93 доллара.
- Сумма займа (PV) = 10 000 долларов США
- Процентная ставка за период (ставка) = 7% в год
- Количество заемных периодов (Nper) = 20 лет
- Платежи по ссуде (PMT) =?
- Выплаты по займам (PMT) = 943,93 $
Вы можете рассчитать процентную ставку, если знаете сумму заимствования, платеж по ссуде и продолжительность ссуды (количество периодов платежей).Например, если вы занимаетесь 10 000 долларов на 20 лет, а ваш платеж по кредиту составляет 943,93 доллара, ваш процентный платеж составляет 7%.
- Сумма займа (PV) 10 000 долл. США
- Платежи по займам (PMT) $ 943,93
- Количество заемных периодов (Nper) = 20 лет
- Процентная ставка (ставка) =?
- Процентная ставка (ставка) = 7%
Вы можете вычислить количество платежей по ссуде, если знаете сумму ссуды, платеж по ссуде и процентную ставку. Например, если вы занимаетесь 10 000 долларов под 7% годовых, а ваш платеж составляет 943,93 доллара, на погашение ссуды уйдет 20 лет.
Например, если вы занимаетесь 10 000 долларов под 7% годовых, а ваш платеж составляет 943,93 доллара, на погашение ссуды уйдет 20 лет.
- Сумма займа (PV) = 10 000 долларов США
- Процентная ставка (ставка) = 7% годовых
- Платежи по займам (PMT) $ 943,93
- Количество заемных периодов (Nper) =?
- Количество заемных периодов (Nper) = 20 лет
Вы можете вычислить заемную сумму, если вам известны платеж по ссуде, процентная ставка и продолжительность ссуды (количество периодов выплат).Например, если ваш платеж по кредиту составляет 943,93 доллара США, процентная ставка составляет 7%, и вы будете возвращать ссуду в течение 20 лет, сумма вашего займа составляет 10 000 долларов.
- Платежи по займам (PMT) $ 943,93
- Процентная ставка (ставка) = 7% годовых
- Количество заемных периодов (Nper) = 20 лет
- Сумма займа (PV) =?
- Сумма займа (PV) = 10 000 долларов США
Финансовый калькулятор или электронная таблица на персональном компьютере может выполнять гораздо больше функций в дополнение к описанным выше.
Дон Хофстранд, бывший специалист по сельскому хозяйству с добавленной стоимостью, [email protected]
Какова текущая стоимость аннуитета?
Аннуитет может быть полезным инструментом при планировании выхода на пенсию. После того, как вы перестанете работать, вы будете полагаться на свои сбережения и выплаты социального страхования, чтобы поддерживать себя и наслаждаться золотыми годами. Покупка аннуитета создает дополнительный поток дохода, который может упростить жизнь.Многие люди работают с финансовым консультантом, чтобы оптимизировать план для достижения своих пенсионных целей. Давайте посмотрим, как рассчитывается текущая стоимость вашего аннуитета и как это может повлиять на ваш выход на пенсию.
Тем не менее, вы можете задаться вопросом о приведенной стоимости приобретенного вами аннуитета. Приведенная стоимость аннуитета — это общая денежная стоимость всех ваших будущих аннуитетных платежей с учетом определенной нормы доходности или ставки дисконтирования. Знание приведенной стоимости аннуитета может помочь вам точно определить, сколько стоимости у вас осталось в приобретенном аннуитете.Это упрощает планирование будущего и принятие разумных финансовых решений.
Знание приведенной стоимости аннуитета может помочь вам точно определить, сколько стоимости у вас осталось в приобретенном аннуитете.Это упрощает планирование будущего и принятие разумных финансовых решений.
Прежде чем мы рассмотрим приведенную стоимость аннуитета, давайте сначала рассмотрим, что такое аннуитет. Аннуитет — это договор, который вы заключаете с финансовой компанией, по которому вы платите премию в обмен на выплаты позже.
Текущая стоимость аннуитета — это денежная стоимость всех ваших будущих аннуитетных платежей. Норма прибыли или ставка дисконтирования является частью расчета.Будущие выплаты аннуитета уменьшаются в зависимости от ставки дисконтирования. Таким образом, чем выше ставка дисконтирования, тем ниже приведенная стоимость аннуитета.
Текущая стоимость аннуитета основана на временной стоимости денег. Вы можете инвестировать деньги, чтобы заработать больше денег за счет процентов и других механизмов возврата, а это означает, что получить 5000 долларов прямо сейчас более ценно, чем обещанные 5000 долларов через пять лет. Норма прибыли, которую вы получите от инвестирования этих 5000 долларов, означает, что к тому времени, когда вы получите 5000 долларов через пять лет, те 5000 долларов, которые вы получите сейчас, будут стоить больше денег.-n)) / r)
Норма прибыли, которую вы получите от инвестирования этих 5000 долларов, означает, что к тому времени, когда вы получите 5000 долларов через пять лет, те 5000 долларов, которые вы получите сейчас, будут стоить больше денег.-n)) / r)
Переменные в уравнении представляют следующее:
- P = текущая стоимость аннуитета
- PMT = сумма каждого аннуитета (в долларах)
- R = процентная ставка или ставка дисконтирования
- n = количество оставшихся платежей
Как вы, возможно, догадались по количеству переменных в формуле, вычисление приведенной стоимости аннуитета может быть непростым делом. Хотя существуют онлайн-калькуляторы, которые могут сделать за вас вычисления, с правильной формулой и регулярной рентабельностью не невозможно рассчитать самостоятельно.Мы подробно объясняем, как использовать формулу ниже.
Как рассчитать текущую стоимость аннуитета Используя приведенную выше формулу, вы можете определить приведенную стоимость аннуитета и определить, является ли получение единовременной выплаты или аннуитета более эффективным вариантом. Вот пример того, как это может работать. Обратите внимание, что эта формула предназначена для регулярного аннуитета.
Вот пример того, как это может работать. Обратите внимание, что эта формула предназначена для регулярного аннуитета.
Допустим, у вас есть выбор: аннуитет в размере 25 000 долларов на 20 лет или единовременная выплата в размере 300 000 долларов со ставкой дисконтирования 5%.-20)) / .05)
Подсчитав, получается 311 555 долларов. Это означает, что для данного конкретного аннуитета стоимость аннуитета превышает единовременную выплату, и вам будет лучше выбрать аннуитетные выплаты, а не единовременную выплату.
Когда рассчитывается приведенная стоимость аннуитета?Приведенная стоимость аннуитета обычно используется для расчета денежной стоимости регулярных платежей при урегулировании судебных споров, пенсионных фондах и ссудах.Он также используется для расчета того, выше или ниже ожидаемая стоимость ипотечного платежа. Эти выплаты иногда называют аннуитетами.
Что такое аннуитет? Аннуитет — это финансовый договор, который вы заключаете со страховой компанией. Вы заплатите определенную сумму авансом или как часть плана платежей, а взамен получите заранее установленный годовой платеж. Вы можете получать аннуитетные платежи на неопределенный срок или в течение заранее определенного периода времени. Регулярные выплаты — одно из преимуществ аннуитета.
Вы заплатите определенную сумму авансом или как часть плана платежей, а взамен получите заранее установленный годовой платеж. Вы можете получать аннуитетные платежи на неопределенный срок или в течение заранее определенного периода времени. Регулярные выплаты — одно из преимуществ аннуитета.
Существует два типа договоров аннуитета:
- Фиксированные аннуитеты предлагают гарантированные процентные ставки, выплачиваемые в течение определенного периода времени.
- Переменные аннуитеты не имеют гарантированных выплат, а это означает, что у вас будет больше свободы вкладывать деньги различными способами, и, таким образом, ваши выплаты будут привязаны к результатам этих инвестиций. Это может привести к более высокой доходности, но также может привести к снижению доходности.
Информация о приведенной стоимости аннуитета может быть полезна при планировании выхода на пенсию и финансового будущего в целом. Если у вас есть возможность выбрать аннуитетную или единовременную выплату, вы захотите узнать, сколько стоят ваши оставшиеся аннуитетные выплаты, чтобы вы могли выбрать. Даже если вы не принимаете такого решения, знание текущей стоимости аннуитета может дать вам более четкое представление о ваших финансах.
Если у вас есть возможность выбрать аннуитетную или единовременную выплату, вы захотите узнать, сколько стоят ваши оставшиеся аннуитетные выплаты, чтобы вы могли выбрать. Даже если вы не принимаете такого решения, знание текущей стоимости аннуитета может дать вам более четкое представление о ваших финансах.
- Если вы думаете о покупке аннуитета, поговорить с финансовым консультантом может быть хорошим выбором. Бесплатный инструмент SmartAsset подберет вам финансовых консультантов в вашем районе за 5 минут.Если вы готовы к сотрудничеству с местными консультантами, которые помогут вам в достижении ваших финансовых целей, начните работу по телефону прямо сейчас.
- Аннуитеты — не единственный вариант получения пенсионного дохода. Если у вас есть 401 (k), вы также захотите узнать вероятную стоимость этой учетной записи, когда вы выйдете на пенсию. Узнайте с помощью калькулятора SmartAsset 401 (k).

- Если вы хотите узнать, сколько денег вам понадобится для выхода на пенсию, пенсионный калькулятор SmartAsset поможет вам выяснить, сколько вам нужно будет отложить, чтобы жить комфортно.
Фото: © iStock.com / mapodile, © iStock.com / SARINYAPINNGAM, © iStock.com / shapecharge
Бен Гейер, CEPF® Бен Гейер — опытный финансовый писатель, который в настоящее время работает экспертом по пенсионным вопросам и инвестициям в SmartAsset. Его работы появлялись на Fortune, Mic.com и CNNMoney. Бен окончил Северо-Западный университет и по совместительству учится в аспирантуре Городского университета Нью-Йорка. Он является членом Общества совершенствования бизнес-редактирования и письма и сертифицированным преподавателем в области личных финансов (CEPF®).Когда он не помогает людям разобраться в их финансах, Бен любит смотреть хоккей, слушать музыку и экспериментировать на кухне. Родом из Александрии, штат Вирджиния, сейчас он живет в Бруклине со своей женой.
 Первоначальная сумма ежемесячного платежа меньше по сравнению с вариантом В. (+)J
Первоначальная сумма ежемесячного платежа меньше по сравнению с вариантом В. (+)J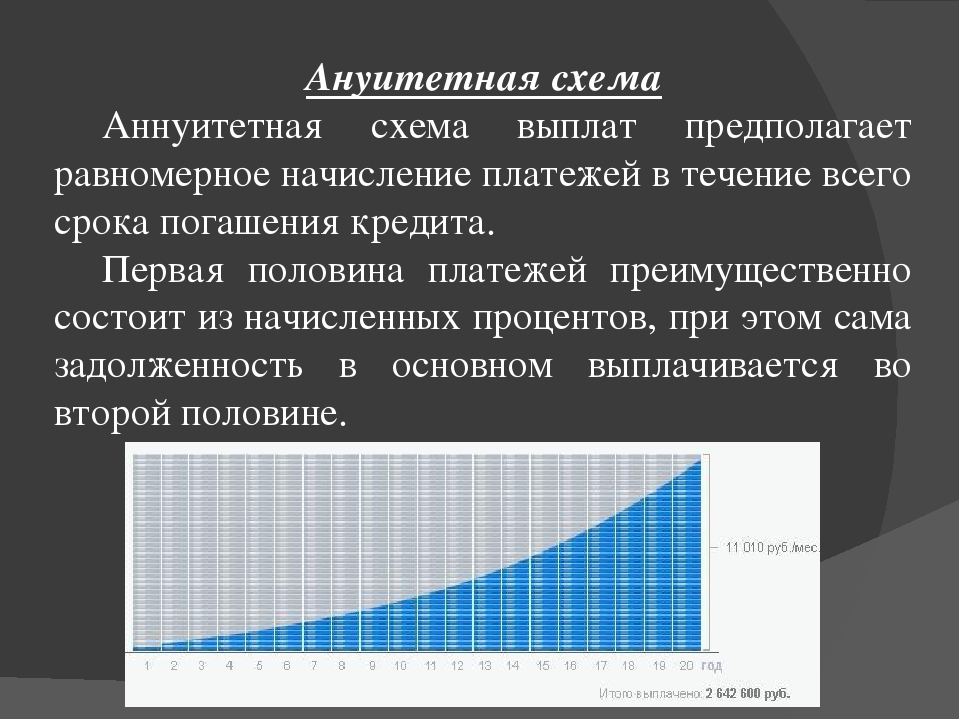 Данный вид кредита встречается не часто и, в основном, для определенной части населения.
Данный вид кредита встречается не часто и, в основном, для определенной части населения. «
« 60
60 В AH 505, стр. 33,
спуститесь на 10 лет и перейдите к столбцу 6, чтобы найти правильный коэффициент 0,135868.
В AH 505, стр. 33,
спуститесь на 10 лет и перейдите к столбцу 6, чтобы найти правильный коэффициент 0,135868.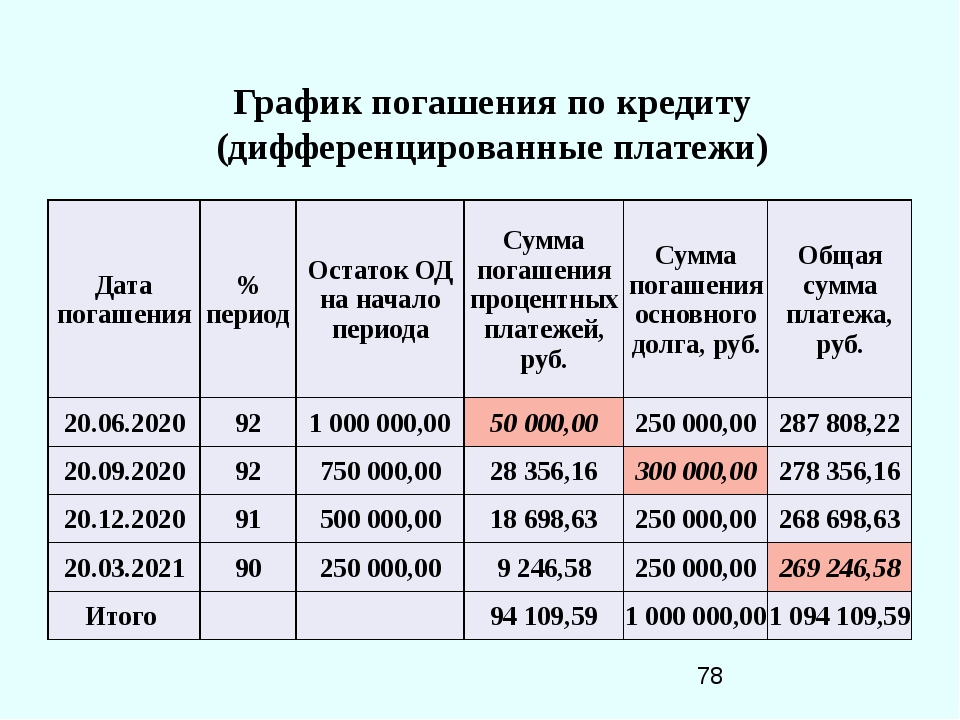

 В AH 505, страница 32, пройдите 18 лет вниз и перейдите к столбцу 5.
чтобы найти правильный ежемесячный коэффициент PW $ 1/ P , равный 131,897876.
В AH 505, страница 32, пройдите 18 лет вниз и перейдите к столбцу 5.
чтобы найти правильный ежемесячный коэффициент PW $ 1/ P , равный 131,897876.