Инженерные Расчёты — Трубы ПНД,ПВХ,гофрированные,для природного газа и сельского хозяйства ,а также все соеденительные детали,производяться нашей компанией КУЗЕЙ БОРУ.Все технические данные Вы сможете увидеть у нас на сайте.

]]>

σk	Давление Стабильности	(N/mm2)
Pk	Давление Критического Коллапса	(bar)
rm	Средний Радиус	(mm)
s	Толщина Стенки	(mm)

4.ИЗМЕРЕНИЕ ДИАМЕТРА ТРУБЫ

Определение участка трубы; баланс непрерывности устанавливается если скорость потока воды на проходе постоянна.

Q=0.0036 . A . v

 Q    : Amount of Load
 A    : Pipe Section
 V    : Скорость Потока
 

Если скорость потока воды постоянна в газовых и паровых проходах, тогда баланс непрерывности устанавливается.

Используется нижеуказанная формула:

m=0.0036 . A . v . ρ

m      : Скорость Потока

ρ       : Плотность Проходимого Материала

 

 5.ПОТЕРИ ДАВЛЕНИЯ

Измерение Отдельных Потерь Давления

 Для того, чтобы измерить высокую энергетическую потерю или потерю давления из-за обьёма потока, скорость потока и давление уменьшают в трубах ПНД, изпользуемая формула указана ниже:

a)   Формула Darc-Weisbach 
   di       : Внутренний Диаметр Трубы (mm)
    I       : Длина Водопровода (mm)
   V       : Средняя Скорость Потока Жидкости (m/s)

     p      : Плотность Жидкости (kg/m3)
    I       : Коэффициент Трения (-)

  Высокие энергетические потери поступают от повышения различий, предназначенные для желаемой скорости потока в линии.

b) Colebrook-White Формула

Re       : Число Рейнольдса
  v          : Кинематическая Текучесть Воды
  k          : Значение Гидравлической Гладкости Внутренней Поверхности Трубы

Формула такова;

V       :Скорость Потока                                               g        :Гравитационное Ускорение
 Je     :Центрирование Энергетической Линии                        : Кинематическая Твёрдость

 Kb     : Рабочая Гладкость                                            d       : Диаметр Трубы

 

  Имются два значения плавности:
              ·  Гладкость плиты ‘k’
              ·  Рабочая гладкость  ‘kb’

 

6.

ВОЗДЕЙСТВИЕ ДАВЛЕНИЯ

При включении или выключения задвижек или насосов, происходит воздействие давления. Таким образом, значение Ps:

a      : Скорость Распространения Волны Давления (m/s)
 vo    : Скорость Потока Жидкости(m/s)
 p      : Плотность Жидкости (kg/m3)

На практике значение Ps может быть как положительным так и негативным. Положительное  значение наблюдается при отключении арматуры и включении насоса. Негативное значение Ps наблюдается при выключенном насосе или при внезапном изменении гидравлического свойства. Скорость распространения волны давления вычисляется по следующей формуле:

7. Полное давление в потоке идеальной жидкости. Метод измерения статического давления и скорости тока жидкости с помощью манометрических трубок.

полное давление у устоявшемся потоке жидкости постоянно вдоль всего потока жидкости.

Закон Бернулли записывают в виде формулы:

где

ρ – плотность жидкости

υ – скорость потока жидкости

h – высота которую занимает отдельный элемент жидкости

р – давление

сonst – напор, или полное давление, или интеграл Бернулли.

Измерение статического давления

Измерение статического давления через отверстие в стенке применяется не только для измерения скорости, но и для многих других целей. Так, например, часто требуется знать распределение давления вдоль поверхности обтекаемого тела. Для этой цели в модели тела (дирижабля, крыла самолета) делается ряд отверстий, которые последовательно соединяются с одним коленом манометра (при этом противодавление в другом колене, конечно, должно быть все время одинаковым). Можно также все отверстия присоединить одновременно к так называемому батарейному манометру, представляющему собой ряд сообщающихся трубок.

Расположение уровней жидкости в таком манометре сразу дает наглядное представление о распределении давления вдоль поверхности тела. хорошо известный опыт, поясняющий уравнение Бернулли для течения в трубе, сначала суживающейся, а затем опять расширяющейся. Дроссельный кран позволяет регулировать скорость, следовательно, и давление в трубе. Если кран открыть полностью, то в самом узком сечении давление настолько понижается, что становится меньше атмосферного. Это легко продемонстрировать, сделав отверстие в нижней части сечения и вставив туда трубку, опущенную в чашку со ртутью.

Заметим, что при таком опыте давление в расширяющейся части трубы получается меньше, чем это следует из уравнения Бернулли, что объясняется некоторой потерей энергии на трение. В суживающейся части, если только сужение происходит плавно (иначе образуются вихри), совпадение с теорией получается очень хорошее. Измерение разности давлений в широкой и узкой частях трубы переменного сечения может быть использовано для определения количества протекающей по трубе жидкости. Примеры распределения давления вдоль поверхности моделей корпуса дирижабля и крыла самолета

8.

Понятия стационарного потока, ламинарное и турбулентное течение. Линии, поверхности тока(слои). Вязкость. Формула ньютона. Коэффициент вязкости. Ньютоновские и неньютоновские жидкости, примеры.

Под стационарным потоком я подразумеваю поток, скорость которого в любом месте жидкости никогда не изменяется. Жидкость в любой точке постоянно заменяется новой жидкостью, движущейся в точности таким же образом. Картина скоростей всегда выглядит одинаково, т. е. v представляет статическое векторное поле. Как в магнитостатике мы рисовали силовые линии, так и здесь можно начертить линии, которые всегда касательны к скорости жидкости. Эти линии называются «линиями тока». Для стационарного потока они действительно представляют реальные пути частиц жидкости. (В нестационарном потоке картина линий тока меняется со временем, однако в любой момент времени она не представляет пути частиц жидкости.)

Вязкость (внутреннее трение) — это свойство реальных жидкостей сопротивляться перемещению одной части жидкости относительно другой.

При таком перемещении возникают силы внутреннего трения, которые направленны по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Ламинарное течение жидкости как правило наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы, при этом наибольшей скоростью обладает слой, который движется вдоль оси трубы.

При турбулентном течении частицы жидкости приобретают составляющие скоростей, которые перпендикулярны течению, и они могут двигаться из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется незначительно. Так как частицы жидкости могут перейти из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

где — градиент скорости, характеризующий быстроту изменения величины скорости в направлении нормали к поверхности трущихся слоев; η- коэффициент пропорциональности, различных для разных жидкостей или газов определяющий их вязкие свойства и называемый коэффициентом динамической вязкости или просто вязкостью.

Физический смысл коэффициента вязкости ясен из формулы (1). Если положить градиент скорости 1=dv/dx и S = 1, то F=η, т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, действующей на единицу площади соприкосновения слоев при градиенте скорости, равном единице.

В СИ динамический коэффициент вязкости измеряется в Паскаль–секундах.

Неньютоновской жидкостью называют жидкость, при течении которой её вязкость зависит от градиента скорости/ Обычно такие жидкости сильно неоднородны и состоят из крупных молекул, образующих сложные пространственные структуры.((каша)))

Нью́тоновская жи́дкость (названная так в честь Исаака Ньютона) — вязкая жидкость, подчиняющаяся в своём течении закону вязкого трения Ньютона, то есть касательное напряжение и градиент скорости линейно зависимы. Коэффициент пропорциональности между этими величинами известен как вязкость(((вода)))

Асламазов Л.Г. Гидростатика // Квант

По специальной договоренности с редколлегией и редакцией журнала «Квант»

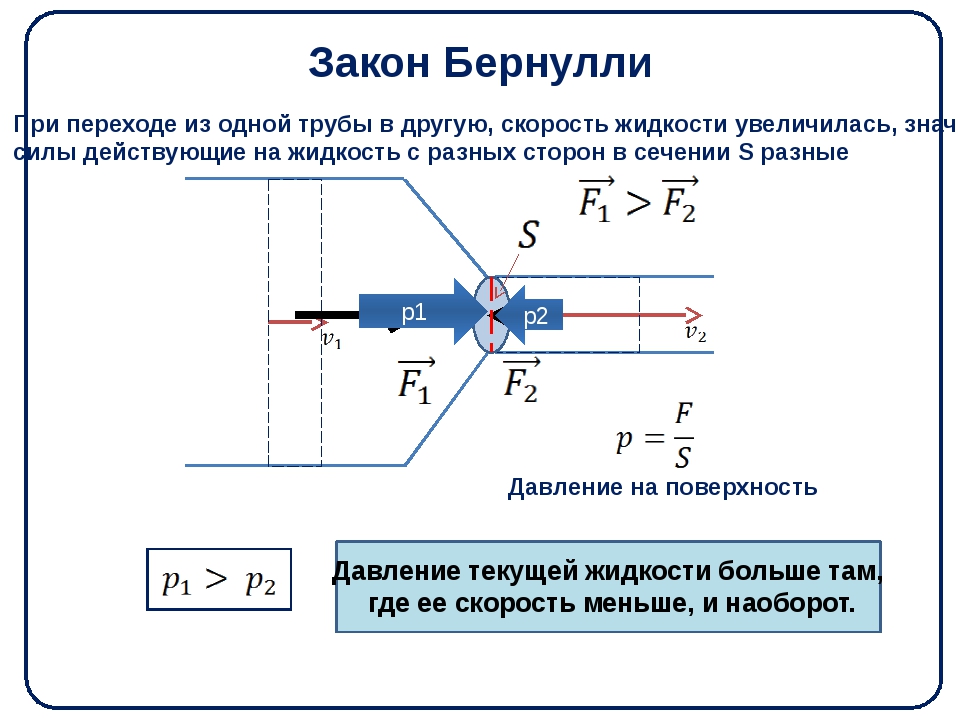
Давление и силы давления

Жидкость оказывает давление на стенки сосуда, в котором она находится, или на любую другую поверхность, соприкасающуюся с ней. Давление – величина скалярная. Оно измеряется абсолютной величиной нормальной (перпендикулярной поверхности) силы, действующей со стороны жидкости на единицу площади поверхности:

Давление в различных точках поверхности может быть разным. Поэтому площадь S мы должны брать достаточно маленькой.

По закону Паскаля давление жидкости не зависит от ориентации поверхности. Как бы ни была расположена поверхность в данном месте жидкости, давление на нее будет одним и тем же.

Сила давления всегда перпендикулярна поверхности. В обычных условиях она направлена так, как если бы жидкость стремилась расшириться.

Задача 1. В сосуд, имеющий форму куба с ребром a, налита доверху жидкость плотностью ρ. Определите силы давления жидкости на дно и стенки сосуда.

Давление жидкости на дно сосуда равно весу столба жидкости высотой a с площадью основания, равной единице: , где g – ускореннее свободного падения.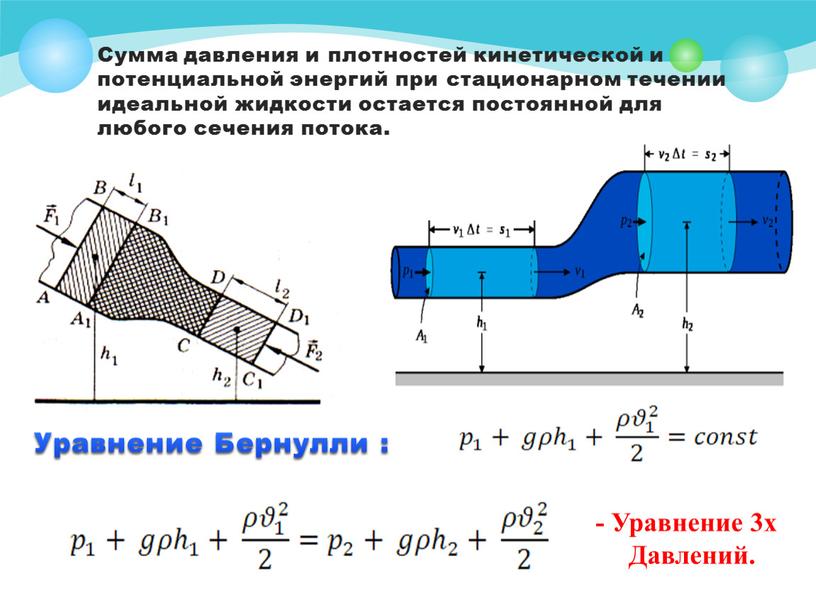 (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)

а

б

Рис. 1

Давление на боковую грань куба будет зависеть от расстояния до поверхности жидкости. На глубине h давление . Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление

умножить на площадь боковой грани

Задача 2. В цилиндрический сосуд диаметром D = 0,7 м вставлен поршень с длинной вертикальной трубкой диаметром d = 0,05 м (рис. 2). Максимальная сила трения между поршнем и стенками сосуда F_тp = 100 Н. Через трубку в сосуд наливают воду. При каком уровне воды в трубке H поршень начнет двигаться? Чему будет равна при этом сила давления воды на дно сосуда? Поршень расположен на высоте h = 0,2 м от дна сосуда. Плотность воды ρ = 10³ кг/м³. Массой поршня с трубкой пренебречь.

Рис. 2

Давление в жидкости на уровне поверхности поршня определяется расстоянием от этого уровня до свободной поверхности жидкости:

Поршень начнет двигаться, когда сила давления на него со стороны жидкости станет равной максимальной силе трения:

где  – плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p₁, находим

Давление на дно сосуда .

Сила давления

Задача 3. Длинная вертикальная труба с поршнем опущена одним концом в сосуд с водой. Вначале поршень находится у поверхности воды, затем его медленно поднимают. Как зависит сила, прикладываемая к поршню, от высоты h ее поднятия? Площадь поперечного сечения трубы S, атмосферное давление p₀. Изменением уровня воды в сосуде, массой поршня и ею трением о стенки трубы пренебречь.

При поднятии поршня вода под действием атмосферного давления будет вначале заполнять трубу (рис 3, а). Давление в трубе на уровне жидкости в сосуде равно атмосферному давлению p₀. Давление воды на поршень меньше атмосферного на величину веса столба жидкости высотой h и площадью основания, равной единице:

а

б

Рис. 3

Сверху на поршень по-прежнему действует атмосферное давление. Поэтому для удержания поршня на высоте h к нему надо приложить силу, равную

и направленную вверх.

С увеличением h давление воды на поршень будет уменьшаться. На высоте

давление обратится в ноль. При дальнейшем поднятии поршня уровень воды в трубе изменяться не будет, тан как сила атмосферного давления, действующая на столб жидкости в трубе снизу, уравновесится силой тяжести. Для удержания поршня на высоте h > h₀ к нему надо приложить силу .

Зависимость прикладываемой к поршню силы F от высоты его поднятия h изображена графически на рисунке 3, б.

Высота столба воды в трубе , очевидно, может служить для измерения атмосферного давлении p₀. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути  = 0,76 м (плотность ртути ρ_рт = 1,36×10⁴ кг/м³).

Примером другого гидростатического устройства, широко используемого в практике, являются сообщающиеся сосуды.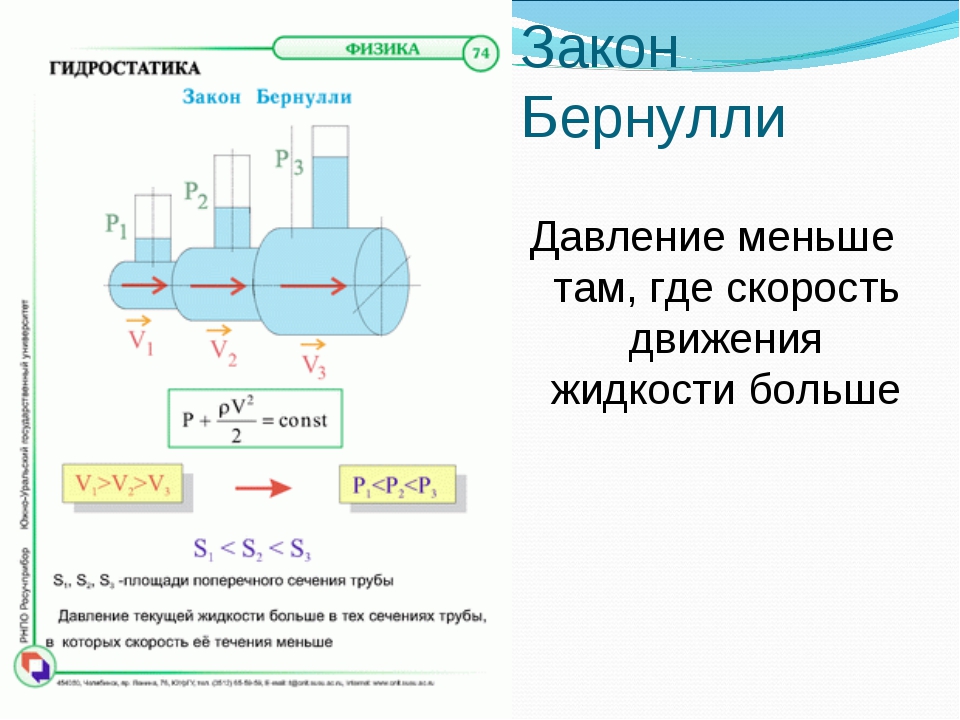 Известен закон сообщающихся сосудов: если давление над жидкостью в сосудах одинаково, то уровни жидкости в них равны. Нетрудно доказать этот закон для случая цилиндрических сосудов (рис. 4). Так как жидкость в соединительной трубке находится в равновесии, то давления на нее с обеих сторон должны быть одинаковы. Поэтому равны и уровни жидкости в сосудах.

Рис. 4

В общем случае для доказательства закона сообщающихся сосудов можно воспользоваться принципом отвердевания, который часто используют в гидростатике. Суть этого принципа заключается в следующем: всегда можно представить себе, что часть жидкости отвердела – равновесие оставшейся части жидкости от этого не нарушится. Так, в цилиндрических сообщающихся сосудах мы можем мысленно выделить часть жидкости, которая заполняла бы сообщающиеся сосуды любой извилистой формы (см. рис. 4), и представить себе, что остальная часть жидкости отвердевает. Тогда равновесие выделенной нами части жидкости не нарушится, и, следовательно, уровни жидкости в извилистых сообщающихся сосудах будут такими же, какими были в цилиндрических сосудах, т. е. одинаковыми.

Закон сообщающихся сосудов справедлив только для однородной жидкости. Если в сосуды налиты жидкости разных плотностей, то уровни в сосудах могут быть разными.

Задача 4. В U – образную трубку налита ртуть. Поверх ртути в одно из колен трубки налили воду (рис. 5, a). Высота столбика воды l = 0,1 м. Определите разность уровней жидкостей в коленах трубки. Нарисуйте график зависимости давления в обоих коленах трубки от высоты. Плотность ртути ρ_рт = 1,36×10⁴ кг/м³, плотность воды ρ_рт = 10³ кг/м³. Атмосферное давление не учитывайте.

а

б

Рис. 5

Давления на ртуть на уровне h_o соприкосновения воды и ртути в обоих коленах должны быть одинаковы (закон сообщающихся сосудов для однородной жидкости). Поэтому

где разность уровней h₂ – h₁ обозначена через Δh. Отсюда

Давление в колене, содержащем только ртуть, меняется с высотой h по закону

Эта формула справедлива и в изогнутой части трубки. (Представите себе, что изогнутое колено сообщается с прямым цилиндрическим сосудом, в котором тоже находится ртуть. Тогда давления на одинаковой высоте в обоих сосудах должны быть равны). В другом колене в области , где находится только вода, давление

Ниже уровня h₀ зависимость давления от высоты дается той же формулой, что и в первом колене:

Зависимость давления в коленах трубки от высоты изображена графически на рисунке 5, б. Как видно, выше уровня h₀ давления на одинаковой высоте разные.

---

Выталкивающая сила

На тело, погруженное в жидкость, как известно, действует выталкивающая сила. Эта сила является равнодействующей сил давления жидкости на тело. Найдем, например, выталкивающую силу, действующую на кубик с ребром a целиком погруженный в жидкость плотностью ρ. Сила давления со стороны жидкости на верхнюю грань кубика равна

где h – расстояние от этой грани до поверхности жидкости (для простоты мы считаем, что плоскость верхней грани кубика параллельна поверхности жидкости). На нижнюю грань кубика действует сила

Силы давления на боковые грани кубика уравновешивают друг друга. Равнодействующая сил давлении, т.е. выталкивающая сила, равна

и направлена вертикально вверх. Мы получили закон Архимеда: выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость.

В общем случае закон Архимеда можно доказать с помощью принципа отвердевания. Мысленно заменим погруженное тело жидкостью. Очевидно, что эта жидкость будет находиться в равновесии. Следовательно, сила тяжести, действующая на нее, уравновешена силами давления со стороны окружающей жидкости. Если теперь представить себе, что выделенная нами часть отвердела, то равновесие оставшейся части не нарушится, и поэтому не изменятся силы давления на отвердевшую жидкость. Равнодействующая этих сил будет по-прежнему равна силе тяжести.

При доказательстве мы считали, что тело целиком погружено в жидкость. Однако аналогичные рассуждения легко провести и в случае, когда только часть тела находится в жидкости (проделайте это сами). И мы опять получим, что выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость:

где ρ – плотность жидкости, V – объем погруженной в жидкость части тела, g –ускорение свободного падения.

Задача 5. На дне водоема установлена П – образная конструкция из трех одинаковых балок, соединенных между собой (рис. 6). Как зависит сила давления этой конструкции на дно от уровня воды в водоеме? Рассмотрите два случая: 1) вода подтекает под опоры; 2) опоры плотно соприкасаются с дном. Балки имеют квадратное сечение со стороной a, длина балки l = 2a. Плотность материала балок ρ₀. плотность воды ρ.

а

б

в

Рис. 6

Сила давления F_д на дно определяется разностью силы тяжести конструкции  и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:

Соответствующий график для силы F_д изображен на рисунке 6, в – он обозначен цифрой 1.

Во втором случае отсутствует давление воды на опоры снизу (рис.6, б), и пользоваться законом Архимеда уже нельзя. Для определения силы F необходимо найти равнодействующую сил давления:

F = 0 при h ≤ a,

Последнее выражение обращается в нуль при  и при больших h становится отрицательным. Это означает, что при  силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.

Задача 6. Пробковый кубик с ребром a = 0,1 м погрузили в воду на глубину h = 0,2 м с помощью тонкостенной трубки диаметром d = 0,05 м (рис. 7). Определите, какой груз надо положить в трубку, чтобы кубик от нее оторвался. Плотность пробки ρ₀ = 200 кг/м³, плотность воды ρ = 10³ кг/м³.

Рис. 7

Вес груза равен разности выталкивающей силы F действующей на кубик, и силы тяжести кубика . Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила . В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:

где  – площадь сечения трубки. Таким образом, сила тяжести грузика

Масса грузика т = 1,2 кг.

Выталкивающую силу, действующую на кубик, можно найти и другим способом. Рассмотрим кубик с трубкой как единое тело, вытесняющее объем воды

Тогда по закону Архимеда на кубик с трубкой действует выталкивающая сила

которая равна выталкивающей силе, действующей на кубик, так как равнодействующая сил давления воды на трубку равна нулю.

Жидкость в движущемся сосуде

Изучим теперь равновесие жидкости в сосуде, движущемся с ускорением. По второму закону Ньютона в этом случае векторная сумма всех сил, действующих на любой выделенный элемент жидкости, должна равняться , где m – масса выделенной жидкости,  – ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна .

Задача 7. Сосуд с жидкостью плотностью ρ падает с ускорением a. Определите давление жидкости на глубине h и силу давления на дно сосуда. Высота уровня воды в сосуде H, площадь дна сосуда s.

Выделим столбик жидкости высотой h с площадью основания s. На него действуют сила тяжести  и сила давления , направленная вверх. Равнодействующая этик сил создает ускорение столбика:

где  – масса столбика. Для давления p на глубине h отсюда находим

Сила давления на дно сосуда

будет тем меньше, чем больше ускорение сосуда a. При  (свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При  жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.

Задача 8. На дне сосуда с жидкостью лежит тело. Может ли тело всплыть, если сосуд начнет двигаться вверх с ускорением? Определите силу давления тела на дно сосуда, если ускорение сосуда a, плотность жидкости ρ₀, плотность тела ρ, его объем V.

На тело, лежащее на дне сосуда, действуют сила тяжести mg сила реакции дна N и выталкивающая сила F (рис. 8). Если сосуд покоится, то сумма этих сил равняется нулю.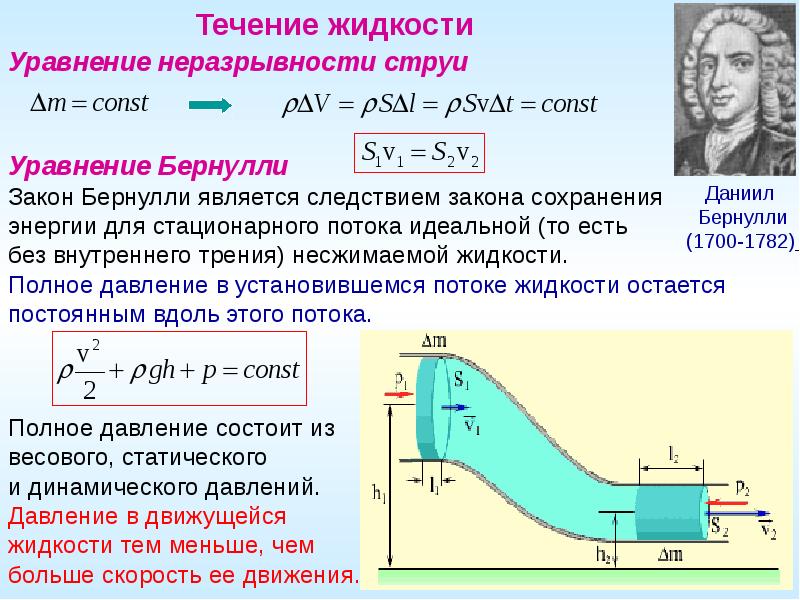 При движении сосуда с ускорением a вверх по второму закону Ньютона имеем

Рис. 8

Определим выталкивающую силу F. Аналогично решению предыдущей задачи, легко получить, что при ускоренном движении сосуда, вверх давление на глубине h дается формулой

т.е. давление в  раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:

где  – масса вытесненной телом воды.

Подставляя это выражение в формулу второго закона Ньютона, для силы реакции дна получаем

Легко видеть, что в сосуде, движущемся с ускорением вверх, сила реакции дна всегда больше, чем в неподвижном. Поэтому тело не только не всплывает, а наоборот, сильнее прижимается ко дну.

Задача 9. Сосуд с жидкостью движется горизонтально с ускорением a. Определите форму поверхности жидкости в сосуде.

Выделим горизонтальный столбик жидкости длиной l и площадью поперечного сечения S (рис. 9). По второму закону Ньютона

где  – масса столбика, p₁ и p₂ – давления на него слева и справа.

  

Рис. 9

Давление на глубине h определяется по обычной формуле  (по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем

или

Но  – это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем .

Заметим, что давление жидкости на данной высоте здесь не одно и то же.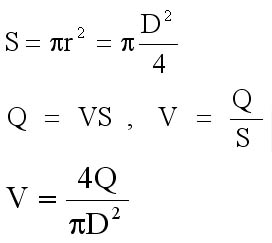 Линии равного давления параллельны поверхности жидкости. Если ввести расстояние h´ от точки до поверхности жидкости, то давление в этой точке

Поэтому можно сказать, что ускоренное движение сосуда эквивалентно замене ускорения свободного падения  на величину . Это утверждение в равной степени относится и к предыдущим двум задачам.

Упражнения

1. Три сосуда, имеющие формы цилиндра, усеченного конуса и перевернутого усеченного конус с одинаковыми площадями оснований и рапными объемами, доверху наполнены водой. Как соотносятся между собой силы давлении воды на дно сосудов?

2. Трубка ртутного барометра подвешена нити. Определите натяжение нити, если высота уровня ртути и трубке Н = 0,76 м, внешний диаметр трубки D = 0,02 м, внутренний d = 0,017 м. нижний конец трубки погружен в ртуть на глубину h = 0,1 м, масса трубки m = 0,3 кг, плотность ртути ρ = 1,36×10⁴ кг/м⁴. Считайте, что торцы трубки плоские.

3. Длинная вертикальная трубка погружена одним концом в сосуд с ртутью. В трубку наливают m = 0,71 кг воды, которая не вытекает из трубки. Определите изменение уровня ртути и сосуде. Диаметр сосуда D = 0,06 м, плотность ртути ρ = 1,36×10⁴ кг/м⁴. Толщиной стоим трубки пренебречь.

4. В сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лед растает? Что будет, если в лед вморожен а) кусочек свинца: б) кусочек пробки?

5. В цилиндрические сообщающиеся сосуды диаметрами D = 0,06 м и d = 0,02 м налита вода. Как изменятся уровни воды в сосудах, если в один из сосудов поместить тело массой т = 0,02 кг, которое будет плавать в воде? Плотность воды ρ = 10³ кг/м³.

6. Сосуд с водой скользит без трения по наклонной плоскости с углом наклона α. Определите, как расположится поверхность воды и сосуде.

Ответы

1. Сила давления на дно наибольшая у сосуда, имеющего форму усеченного конуса, наименьшая – у перевернутого конуса.

2.

3.

4. Если лед чистый или в него вморожен кусочек пробки, то уровень воды не изменится. Если же в лед вморожен кусочек свинца, уровень воды понизится.

5.

6. Поверхность параллельна наклонной плоскости.

Типы давления: абсолютное давление, избыточное давление, дифференциальное давление

Наравне с температурой давление является одним из наиболее важных параметров, описывающих физическое состояние среды. Давление определяется как сила (F_N), постоянно действующая на заданную площадь поверхности (A). Типы давления отличаются друг от друга только по отношению к выбранному эталонному давлению.

Абсолютное давление

Наиболее приемлемым эталонным давлением является нулевое, которое существует в безвоздушном космическом пространстве. Любое давление относительно данного известно как абсолютное. Для отличия такого давления от других типов оно обозначается как “ abs”, что является сокращением от латинского слова “absolutus”, означающего отдельный, независимый.

Атмосферное давление

Наверное наиболее важным типом давления для жизни на земле является атмосферное давление, p_amb (amb = ambiens = окружающий). Это давление образовано массой атмосферы, окружающей землю на высоте примерно до 500 км. До этой высоты, на которой абсолютное давление p_abs = 0, его величина постоянно уменьшается. Тем не менее, атмосферное давление подвержено погодным колебаниям, что хорошо нам известно из ежедневного прогноза погоды. На уровне моря p_amb в среднем составляет 1013,25 гектопаскаля (ГПа), что соответствует 1013,25 миллибара (мбар). Благодаря “циклонам” и “антициклонам” это давление может колебаться в пределах, примерно, 5 %.

Дифференциальное давление

Разница между двумя величинами давления p₁ и p₂ известна как перепад давления
Δp = p₁ — p₂. В случаях, когда разница между двумя значениями представляет собой измеренное значение переменной процесса, говорят о дифференциальном давлении p_1,2.

Избыточное (манометрическое) давление

К наиболее часто встречающемуся типу измеряемого давления на технологических объектах относится перепад атмосферного давления, P_e (e = excedens = превышение). Оно представляет собой разницу между абсолютным давлением P_abs и относительным (абсолютным) атмосферным давлением (p_e = p_abs – p_amb), более известное как избыточное или манометрическое давление.

Понятие положительного избыточного давления используют, когда абсолютное давление превышает атмосферное. В противном случае говорят об отрицательном избыточном давлении.

Сокращения в формулах “abs”, “amb” и “e” однозначно указывают на тип измеряемого давления. Эти сокращения относятся в формулах к букве Р, но не к единицам измерения.

---

Неважно какое давление — абсолютное, избыточное или дифференциальное.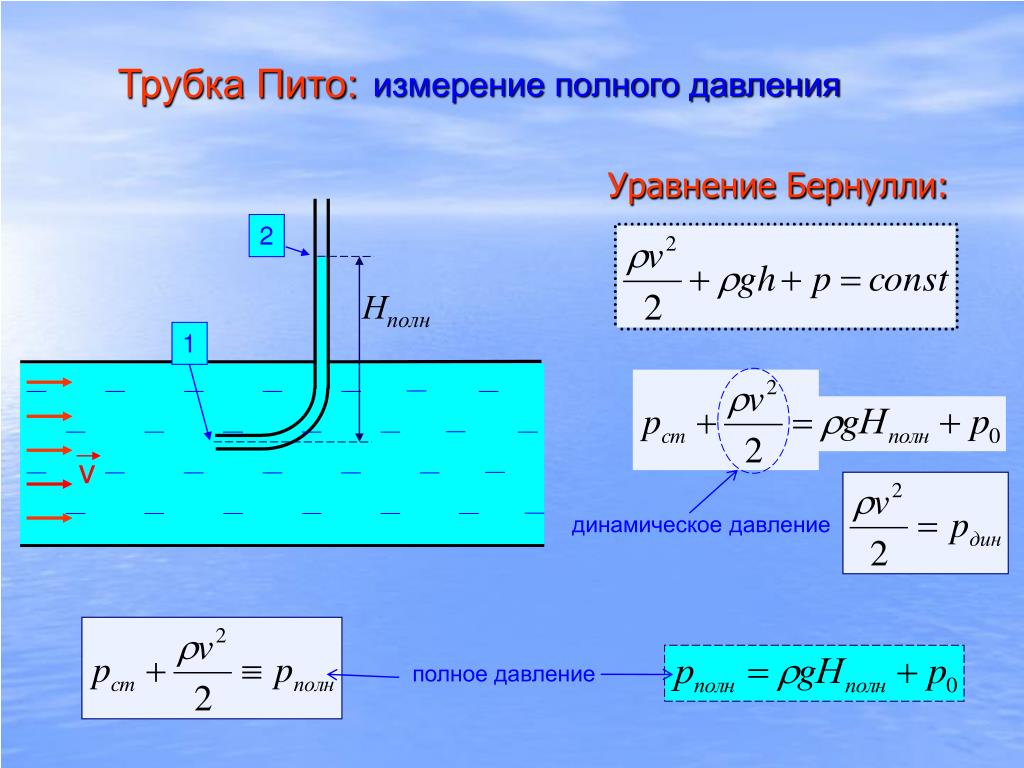 С помощью WIKA вы подберете необходимый измерительный прибор для любого типа давления:

Свяжитесь с нами

Вам нужна дополнительная информация? Напишите нам:

Давление разрыва — что это такое и почему это так важно — Коррозионные материалы

Когда кто-то спрашивает о давлении разрыва трубы, лучший ответ — теоретический. Давление разрыва — это буквально давление, с которым сосуд высокого давления, такой как труба или труба, может выдержать перед разрывом или «разрывом». Условия окружающей среды и другие факторы могут сыграть роль в отказе трубы. Проектирование сосуда высокого давления и выбор материала, который будет использоваться, могут быть сложным процессом.Необходимо обратиться к соответствующему коду ASME BPVC и не следует упрощать процесс путем определения только приблизительного давления разрыва трубы или трубы. Существуют формулы, которые можно использовать для оценки давления разрыва трубы или насосно-компрессорной трубы. Следующее следует использовать только в качестве справки. Corrosion Materials не несет ответственности за любые убытки, которые могут возникнуть в случае использования представленной информации каким-либо иным образом, кроме справочной.

Две наиболее часто используемые формулы — это уравнения Барлоу и Ламе.Давление разрыва зависит от прочности материала и размеров сосуда под давлением (т. Е. Толщины стенки, внутреннего и внешнего диаметра). Температура также может влиять на давление разрыва, поскольку колебания температуры могут иметь прямое влияние на прочность материалов. Следующее обсуждение будет учитывать только условия комнатной температуры, и эту информацию следует использовать только в качестве руководства или справки. При расчете рабочего давления необходимо учитывать коэффициент безопасности.

Уравнение Барлоу предназначено для расчета внутреннего давления. Это может быть давление разрыва или давление текучести в зависимости от того, какое свойство материала используется в уравнении. Из этого уравнения можно извлечь довольно много информации, но важно то, что у вас есть определенная цель. Если вы хотите знать, в какой момент материал начнет пластически или необратимо деформироваться, вы можете использовать предел текучести. Вот почему предел прочности на разрыв используется для определения давления разрыва или точки, при которой материал в конечном итоге разрушается.

Формула Ламе — Формула Барлоу — хорошая формула для всех труб, трубок и цилиндров. Эта формула была упрощена из полного решения Ламе. Ниже представлена ​​упрощенная итерация формулы Ламе.

Воспользуйтесь нашим онлайн-калькулятором давления разрыва с использованием уравнения Барлоу. Введите в форму значения прочности на разрыв (PSI), толщины стенки (дюймы) и внешнего диаметра (дюймы). Кнопка «Вычислить» рассчитает разрывное и рабочее давление.Если у вас нет всей информации для калькулятора и вам нужна техническая помощь по вашему проекту, позвоните по телефону 1-800-455-2276, чтобы поговорить с Якобом Родригесом, нашим специалистом по металлургии и техническим службам.

Ссылки:
Кодекс ASME по котлам и сосудам под давлением, раздел VIII, разд. 1, Таблица UNF-23-3, Par.UG-27 и Приложение 1, Par. 1-2
Стальная труба: руководство по проектированию и установке , 4-е изд. (M11), стр. 45, штат Американской ассоциации водопроводных сооружений.
Справочник по нефтяной промышленности , Том 2 , стр.721, отредактированный Дэвидом Талботом День

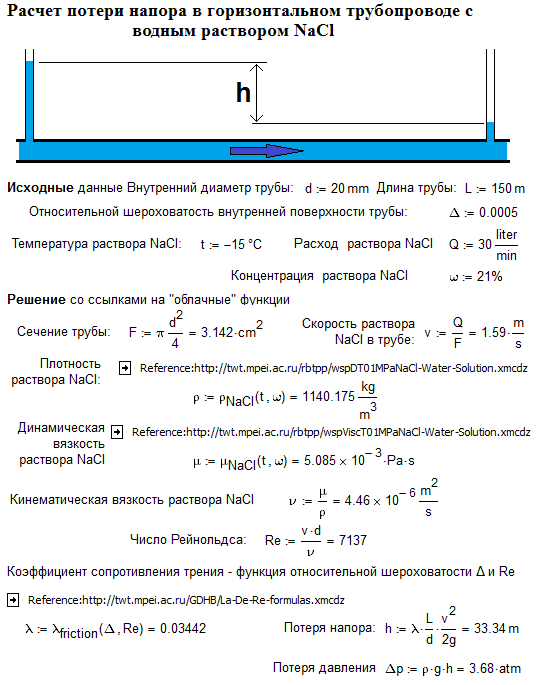
Связь между падением давления и расходом в трубопроводе

Изменение давления из-за потери напора

Поскольку потеря напора — это уменьшение общей энергии жидкости, она представляет собой снижение способности жидкости выполнять работу. Потеря напора не снижает скорость жидкости (рассмотрим трубу постоянного диаметра с постоянным массовым расходом) и не будет влиять на высоту напора жидкости (рассмотрите горизонтальную трубу без изменения высоты от входа к выходу).2} {2g}}

где:

• H _L = потеря напора (футы)
• f = коэффициент трения Дарси (безразмерный)
• L = длина трубы (футы)
• D = внутренний диаметр трубы (футы)
• v = скорость жидкости (фут / сек)
• g = гравитационная постоянная (32,2 фута / сек ² )

Коэффициент трения Дарси, f, учитывает шероховатость трубы, диаметр, вязкость жидкости, плотность и скорость сначала рассчитав число Рейнольдса и относительную шероховатость. 5} \ bigg)}

где:

• Q = расход (галлонов в минуту)
• d = диаметр трубы (дюймы)

На приведенном ниже графике показано результирующее падение давления для воды при 60 F в диапазоне скоростей потока для 100 футовая труба для труб диаметром 4 и 6 дюймов сортамент 40.

Сводка

Чтобы определить общее изменение статического давления жидкости при ее движении по трубопроводу, все три компонента уравнения Бернулли необходимо рассматривать по отдельности и складывать вместе.Изменение высоты может вызвать снижение давления, изменение скорости может привести к его увеличению, а потеря напора может вызвать его уменьшение. Чистый эффект будет зависеть от относительной величины каждого изменения.

Возможно, что статическое давление жидкости действительно увеличивается от входа к выходу, если изменение высоты или скорости приводит к увеличению давления больше, чем уменьшение, вызванное потерей напора.

Старая поговорка о том, что «жидкость всегда течет от высокого давления к низкому», не совсем точна.Более точный способ сформулировать это так: «жидкость всегда течет из области с более высокой полной энергией в область с более низкой полной энергией».

Все датчики Точки давления — это советы по применению, позволяющие упростить проектирование с помощью датчиков давления в микроэлектромеханических системах (МЭМС) и избежать распространенных ошибок.

Точка давления 11: Расчет расхода на основе измерений давления

Поток жидкости возникает при движении жидких и газообразных материалов, и датчики давления играют решающую роль в определении многих аспектов потока жидкости.Гидродинамика обеспечивает средства понимания параметров, влияющих на поток жидкости. Активные ссылки в следующих разделах предоставляют более подробную информацию.

Основные понятия гидродинамики

Число Рейнольдса (Re) — это безразмерное значение скорости, используемое для прогнозирования характера потока. Это функция силы инерции (ρ u L) и силы вязкости или трения (μ).

Вязкостные и невязкие потоки

Вязкий поток приводит к потере энергии (и, как следствие, к повышению температуры), но идеальные жидкости имеют невязкий поток без потерь энергии.

Ламинарный (устойчивый) против турбулентного потока

В ламинарном потоке частицы движутся очень равномерно / упорядоченно, образуются прямые линии, параллельные стенкам корпуса, и очень предсказуемо. При турбулентном потоке случайное движение может привести к образованию водоворотов и другого менее предсказуемого поведения. Смесь ламинарного и турбулентного потоков, называемого переходным потоком, возникает в трубах и других корпусах с турбулентностью в центре корпуса и ламинарным потоком по краям.Более вязкие жидкости имеют тенденцию к ламинарному течению и более низкому числу Рейнольдса.

Сжимаемый или несжимаемый поток

В отличие от сжимаемого потока, где плотность изменяется в зависимости от приложенного давления, в несжимаемом потоке плотность постоянна в пространстве и времени.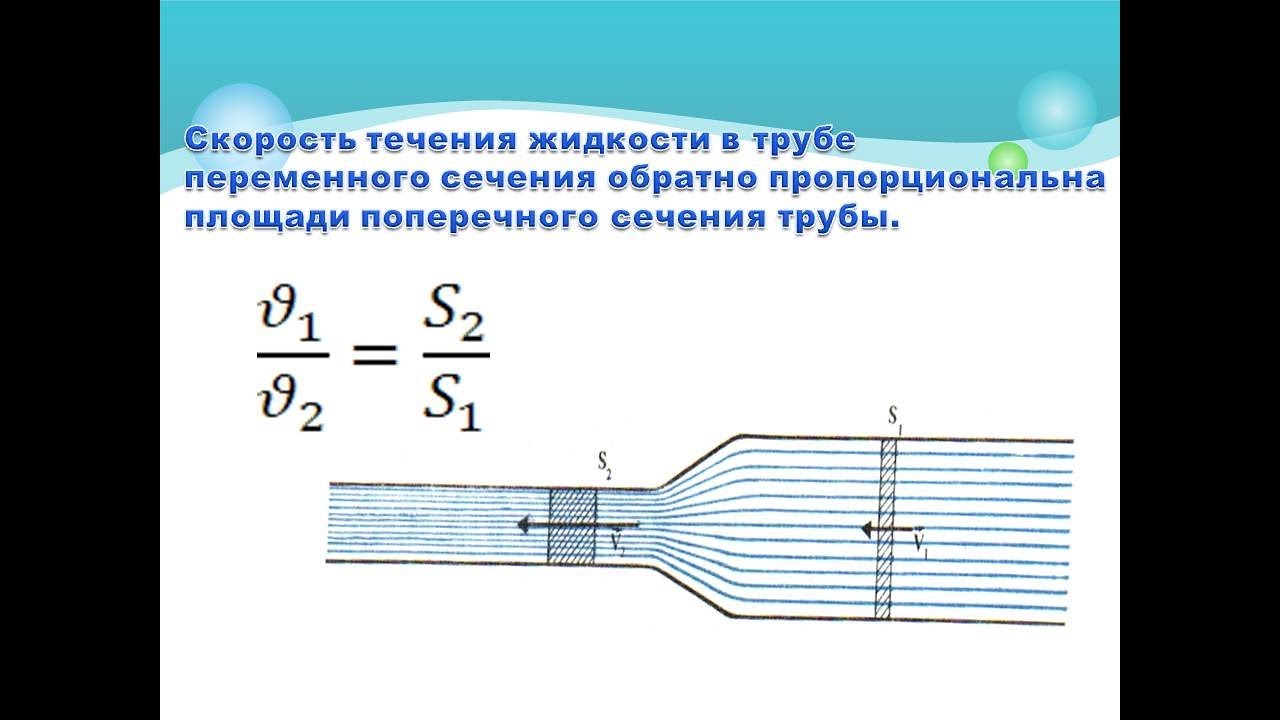

Уравнение Бернулли используется для определения скорости жидкости посредством измерения давления. Он начинается с определения невязкого, устойчивого несжимаемого потока при постоянной температуре.

P + ½ρv ² + ρgy = постоянная

P = давление

v = скорость

ρ = плотность жидкости

г = плотность

y = высота

Эффект Вентури — это увеличение скорости, возникающее при ограничении потока жидкости. Измеритель Вентури представляет собой приложение уравнения Бернулли. Общие типы ограничений включают диафрагмы, трубки Вентури, сопла и любую конструкцию, которая имеет легко измеряемый перепад давления.

Поток в трубе / трубе. Несколько факторов определяют перепад давления, возникающий при работе с потоком жидкости, включая ламинарный и турбулентный поток, скорость потока, кинематическую вязкость и число Рейнольдса жидкости, внутреннюю шероховатость внутренней части трубы, а также ее диаметр, длину и форм-фактор. . Диафрагмы, трубки Вентури и сопла упрощают ситуацию. В этих случаях (см. Рисунок 1) расход связан с ΔP (P ₁ -P ₂ ) уравнением:

q = c _d π / 4 D ₂ ² [2 (P ₁ — P ₂ ) / ρ (1 — d ⁴ )] ^1/2

Где:

q — расход, м ³ / с

c _D — коэффициент расхода, коэффициент площади = A ₂ / A ₁

P ₁ и P ₂ в Н / м ²

ρ — плотность жидкости в кг / м ³

D ₂ — внутренний диаметр отверстия, трубки Вентури или сопла (в м)

p1 «> D ₁ — диаметр трубы до и после трубы (в м)

и d = D ₂ / D ₁ отношение диаметров

Рисунок 1.Элементы измерения расхода ΔP.

Трубки Пито используют разницу между общим давлением и статическим давлением для расчета скорости самолета или жидкости, протекающей в трубе или корпусе. Трубка Пито для измерения скорости самолета показана на рисунке 2.

Рис. 2. Статическая трубка Пито или трубка Прандтля, используемая для измерения скорости самолета.

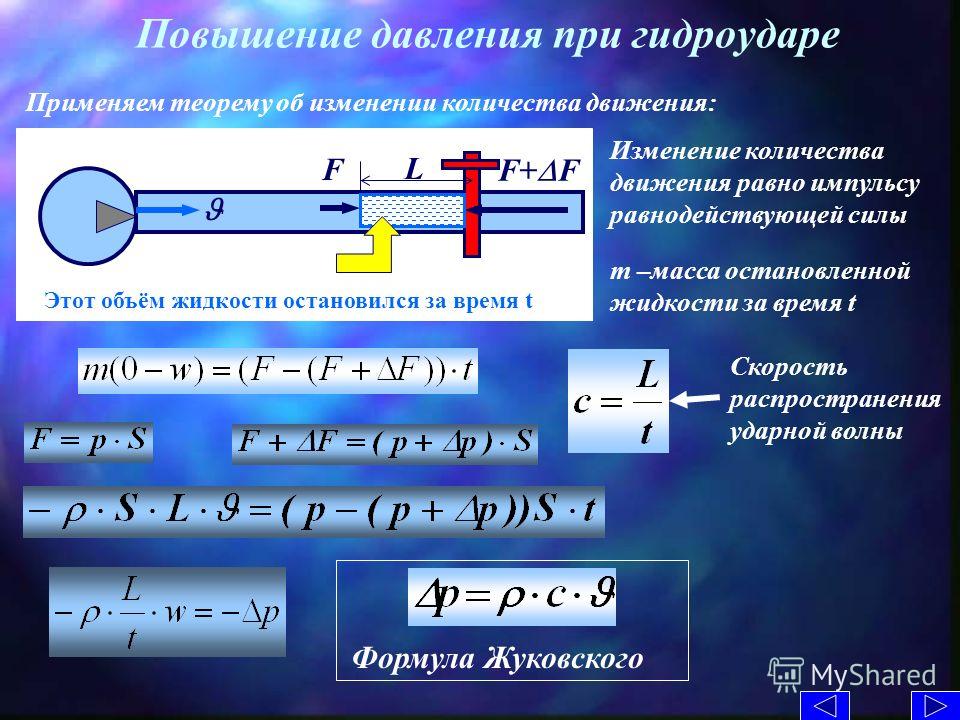
Гидравлический удар — это удар, вызванный внезапным уменьшением скорости протекающей жидкости и времени, которое требуется для волны давления для прохождения в трубе туда и обратно.Уравнение импульса Жуковского используется для расчета результирующего давления, когда скорость жидкости падает до нуля при контакте с закрытым клапаном.

∆P = ρ · c · ∆V

дюйм psf

Для жестких труб скорость волны давления или скорость волны c определяется по формуле:

c = √ E _B / ρ

, где E _B — модуль объемной упругости жидкости в фунтах на квадратный дюйм, а ρ — плотность жидкости.

Измерения в специальных приложениях

В области медицины респираторные проблемы требуют измерения воздушного потока для вентиляции / управления потоком и анализа, такого как спирометры, а также измерения потока газа и жидкости для лечения. Например, перепад давления в спирометре или респираторе номинально составляет 4 кПа, а в аппарате ИВЛ — 25 см H ₂ О. В любом случае значения довольно низкие, и измерение давления требует особого учета давления. датчик для достижения желаемой точности и точности.

ОВК

Чистота и низкое энергопотребление в системах отопления, вентиляции и кондиционирования воздуха (HVAC) требуют наличия надлежащих воздушных фильтров и частого мониторинга для определения фильтра, который требует замены. Нормальное рабочее давление обычно находится в диапазоне от 0,1 до 1 дюйма H ₂ O. Минимальное отчетное значение эффективности Американского общества инженеров по отоплению, охлаждению и кондиционированию воздуха (ASHRAE), или рейтинг MERV, измеряет эффективность воздушных фильтров. .Измерение падения давления на воздушном фильтре сводит к минимуму ненужное потребление энергии двигателями.

Инструменты для расчета и моделирования жидкостей

Инструменты онлайн-расчетов от efunda, KAHN, LMNO Engineering, клапаны, онлайн-калькулятор перепада давления и другие могут предоставить некоторые быстрые инструменты для выполнения расчетов, показанных ранее. Кроме того, несколько компаний предлагают расширенные инструменты моделирования для вычислительной гидродинамики и консультационные услуги, чтобы глубже вникнуть в более сложные и сложные проблемы, связанные с потоком жидкости, в том числе: ANSYS, Applied Flow Technology, Autodesk, MathWorks, SOLIDWORKS и другие.

Расчетное давление — обзор

В этом разделе изложены минимальные технические требования для безопасного проектирования наземных трубопроводов в пределах свойств заводов, перерабатывающих нефть, газ и нефтехимические продукты.

3.13.1 Конструкция трубопровода

Расчетное давление для системы трубопроводов должно определяться в соответствии с ASME B 31.3 со следующими дополнениями:

1.

Если давление ограничено предохранительным устройством, конструкция давление не должно быть меньше, чем давление, которое будет существовать в трубопроводных системах, когда устройство для сброса давления начинает сбрасывать давление, или установленное давление устройства для сброса давления, в зависимости от того, что больше.

Следует учитывать максимальную разницу в давлении между внутренней и внешней стороной любого компонента трубопровода или между камерами комбинированного устройства (например, трубы с рубашкой), включая потерю внешнего или внутреннего давления.

Трубопроводы, подверженные разрежению, должны быть рассчитаны на разрежение 100 кПа (1 бар), если не предусмотрен вакуумный прерыватель или подобное устройство. В этом случае может быть одобрено более высокое расчетное давление.

Значение расчетного давления, которое будет использоваться, должно включать статический напор, если это применимо, если это не учитывается отдельно.

Расчетное давление в трубопроводной системе, подверженной внутреннему давлению, определяется как одно из следующих:

1.

Расчетное давление оборудования, к которому подсоединяется трубопровод

2.

Установленное давление предохранительного клапана системы трубопроводного оборудования (если ниже [a])

3.

Давление не ниже давления отключения или давления, возникающего в результате суммы максимального давления всасывания плюс 1.2-кратный расчетный перепад давления для нагнетательных линий насосов и / или компрессоров, не защищенных предохранительным клапаном

4.

Максимальные перепады давления между внутренней и внешней стороной любого элемента трубопровода или между камерами комбинированного агрегата ( Например, труба с рубашкой) следует учитывать, включая потерю внешнего или внутреннего давления

Трубопровод, подверженный воздействию вакуума, должен быть рассчитан на разрежение 100 кПа (15 фунтов на квадратный дюйм), если не предусмотрен вакуумный прерыватель или подобное устройство .

Расчетная температура должна определяться в соответствии с ASME Code B 31.3 со следующими дополнениями:

1.

Расчетная температура должна включать достаточный запас для покрытия неопределенности в прогнозировании температуры.

2.

Расчетная максимальная температура не должна быть меньше фактической температуры металла, ожидаемой при эксплуатации, и должна использоваться для определения соответствующего расчетного напряжения «S» для выбранного материала.

В случае, если внешние компоненты имеют теплоизоляцию, самая низкая температура металла должна приниматься за минимальную температуру содержимого трубы.

Рабочая температура трубопровода должна определяться как температура, соответствующая температуре жидкости при нормальных рабочих условиях.

В случае трубопровода с паровым обогревом рабочая температура должна приниматься равной одному из следующих значений:

1.

Температура равна 70% от рабочей температуры пара, если традиционный электрогидравлический обогреватель используется без использование теплопроводного цемента, а также когда температура пара выше рабочей температуры технологической жидкости

2.

Рабочая температура пара при трассировке с использованием теплопроводящего цемента

3.

Рабочая температура пара в случае трубопровода с рубашкой

Выбор типа и материала трубы должны соответствовать стандартам. Для кислых сред необходимо учитывать требования NACE.MR 01-75.

Требуемую толщину труб следует определять в соответствии со стандартом ASME B 31.3: 2004.

Выбор стандартной толщины стенок труб должен соответствовать ASME B 36.10М: 2004.

1.

Радиус изгиба должен быть указан на изометрическом чертеже, но в принципе он не должен быть меньше чем в пять раз больше номинального диаметра трубы.

2.

Все гибки труб из нержавеющей стали и никелевых сплавов должны выполняться в холодном состоянии. Если размер и характеристики трубы таковы, что холодная гибка становится невозможной, необходимо подготовить процедуру горячей гибки и последующей термообработки на твердый раствор для рассмотрения и утверждения инженером.

3.

Обычно снятие напряжений не считается необходимым для холодногнутой нержавеющей стали и высоконикелевых сплавов, но в случае аустенитных нержавеющих сталей может потребоваться некоторое снижение уровня остаточного напряжения после холода. изгиб (например, в случае, когда изгиб подвергается воздействию хлорида или политионовой кислоты).

Если снятие напряжений указано инженером, напряжение изгиба должно быть снято путем быстрого нагрева до температуры 900–950 ° C и выдержки в течение 1 ч / толщины 25 мм в течение минимального периода 1 ч с последующим охлаждением на неподвижном воздухе.Нагревание должно осуществляться либо с помощью местных электрических одеял, либо с помощью печи. В последнем случае топочный газ должен иметь контролируемое содержание серы.

4.

Для ферритных сталей, за исключением закаленных и отпущенных марок, должна применяться нормализующая термообработка, если холодная деформация превышает 15% или когда увеличение твердости по Виккерсу или Бриннеллю больше более 100.

5.

Для закаленных и отпущенных ферритных сталей следует применять соответствующую термическую обработку для снятия напряжений, если холодная деформация составляет более 15% или когда повышение твердости по Виккерсу или Бриннеллю превышает 100.Снятие напряжений должно быть как минимум на 10 ° C ниже температуры отпуска.

Вытяжные отводы с радиусом изгиба по центральной линии не менее пятикратного номинального размера трубы (NPS) могут изготавливаться для труб диаметром до DN 40 включительно (NPS 1,5).

•

Угловые отводы (дополнение к ASME B 31.3)

Угловые отводы не следует использовать, если давление превышает 500 кПа (72,5 фунта на кв. Дюйм) или где коэффициент уменьшения диапазона напряжений « f » в случае циклического изменения температуры или давления будет <1.

Краткий обзор испытательных, разрывных и рабочих давлений

Черная оцинкованная труба

Wheatland Schedule 40, изготовленная в соответствии со спецификацией ASTM A53, предназначена для механических применений и применений под давлением. Сфера применения стандарта ASTM A53 гласит: «Труба, заказанная в соответствии с этой спецификацией, предназначена для механических применений и применений под давлением, а также приемлема для обычного использования в линиях пара, воды, газа и воздуха». Трубы для использования под давлением также важны для спринклерных трубопроводов, труб API Line, труб и обсадных труб, а также для изготавливаемых нами соединительных муфт.

Чтобы помочь вам различать типы испытательного, рабочего и разрывного давления, ниже приводится краткий обзор.

Испытательное давление

Испытательное давление относится к испытанию гидростатическим (водяным) давлением, применяемому на мельнице. Это контрольное устройство, используемое для проверки целостности тела трубы и сварного шва.

Общее правило, применяемое при выборе испытательного давления, состоит в том, что испытательное давление должно превышать рабочее давление, которому труба обычно будет подвергаться. Однако испытательное давление увеличивается с увеличением толщины стенки трубы

Для труб непрерывной стыковой сварки (CBW) и электросварки сопротивлением (ERW) испытательное давление, приложенное на стане, обычно рассчитывается по постоянной математической формуле, известной как «уравнение Барлоу»:

P = 2St / D
P = Испытательное давление
S = Нормальный заданный предел текучести материала, 60% от текучести
t = Толщина стенки
D = Номинальный внешний диаметр

Для трубы класса A, где минимальный указанный предел текучести составляет 30 000 фунтов на квадратный дюйм, коэффициент S равен 18 000. Для трубы класса B, где минимальный заданный предел текучести составляет 35 000 фунтов на квадратный дюйм, коэффициент S равен 21 000. Следовательно, для труб аналогичного диаметра труба класса B имеет более высокое испытательное давление, потому что она изготовлена ​​с более высоким уровнем прочности.

Два правила также применяются к выбору испытательного давления:

1. Испытательные давления, определенные по формуле, должны быть округлены до ближайших 50 фунтов на квадратный дюйм для давлений ниже 1000 фунтов на квадратный дюйм и до ближайших 100 фунтов на квадратный дюйм для давлений более 1000 фунтов на квадратный дюйм.
2. Независимо от значения, указанного в формуле, испытательное давление никогда не должно превышать 2 500 фунтов на квадратный дюйм для внешних диаметров 3,500 дюймов или менее или 3000 фунтов на квадратный дюйм для внешних диаметров более 3,500 дюймов.

Есть две причины для оправдания правила № 2 в отношении ограничения максимального испытательного давления. Одна из причин заключается в том, что в трубе обычно не будет рабочего давления выше указанного максимального значения. Другая причина заключается в том, что испытание отдельных отрезков до более высоких давлений увеличивает риск того, что давление приведет к изгибу или изгибу трубы, что потребует повторного выпрямления трубы.

Давление разрыва

Давление разрыва относится к внутреннему давлению, которое вызывает разрыв или разрыв трубы.

Номинальное давление разрыва также рассчитывается по уравнению Барлоу. Однако коэффициент S выбран как минимальная заданная прочность на разрыв используемой трубы.

Для трубы класса A значение S составляет 48 000 фунтов на кв. Дюйм, а для трубы класса B значение S составляет 60 000 фунтов на квадратный дюйм. Вышеуказанные значения используются как для бесшовных, так и для электросварных труб, поскольку эти изделия считаются полностью однородными по прочности по окружности.

Рабочее давление

Рабочее давление — это термин, используемый для описания максимально допустимого давления, которому может подвергаться трубный продукт во время эксплуатации.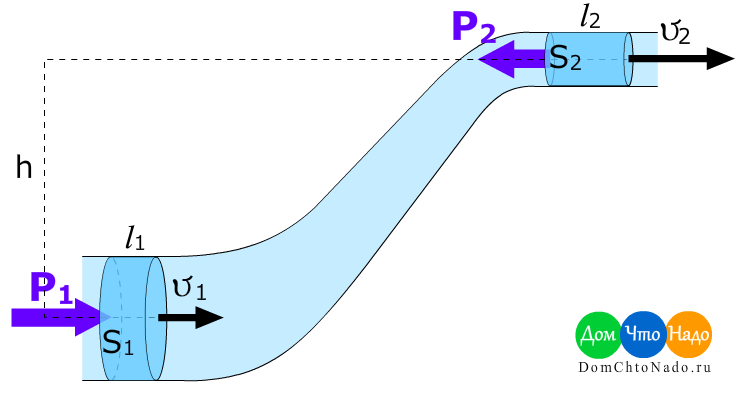 Это включает в себя так называемые «скачки давления».

В Wheatland мы используем формулы из Кодекса по силовым трубопроводам ASME B31.1 2014 года в качестве руководства для определения максимального рабочего давления. Следует использовать коэффициенты безопасности, включенные в руководство, но оно не отменяет никаких федеральных, государственных и местных кодексов или юрисдикций.Просто помните: некоторые государственные и местные нормы и правила накладывают дополнительные ограничения на фактическое рабочее давление.

Для получения дополнительной информации о испытательных, разрывных и рабочих давлениях свяжитесь с менеджером по техническим вопросам Wheatland Майком Райаном по адресу [email protected].

Теги: Испытание давлением, Стальная пожарная спринклерная труба

Консультации — Инженер по подбору | Как выполнить анализ напряжения трубы

Автор: Монте Энгелькемьер, ЧП, PMP, Cargill, Wayzata, Миннесота.21 сентября 2017 г.

Цели обучения

• Определите и оцените процесс анализа напряжений трубы.
• Понимание анализа напряжений труб.
• Узнайте, как моделировать систему трубопроводов и основы расчета давления.

---

Анализ напряжений в трубе — это аналитический метод определения поведения трубопроводной системы в зависимости от материала, давления, температуры, жидкости и опоры. Анализ напряжений труб не дает точного описания поведения трубопроводов, но дает хорошее приближение.

Аналитический метод может включать осмотр, простые или сложные ручные вычисления или компьютерную модель. Компьютерные модели могут варьироваться от одномерных балочных элементов до сложных конечно-элементных моделей. Например, если это водная система, к которой не прилагаются внешние силы, обычно достаточно осмотра или ручных расчетов. Если это система с высоким давлением, высокой температурой, опасными жидкостями и / или большие внешние силы применяются к системе трубопроводов, может потребоваться компьютерная модель.

Программное обеспечение для анализа напряжений в трубах не дает прочной основы для анализа напряжений в трубах.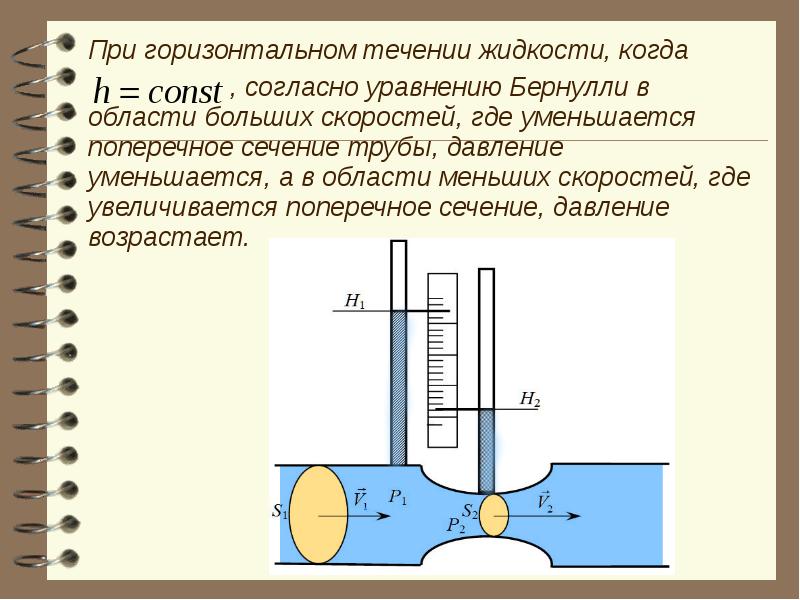 Важно понимать различные типы напряжений в трубах, процессы и другие элементы, связанные с анализом напряжений в трубах, чтобы получить наилучшие методы выполнения анализа напряжений в трубах.

Существует множество кодексов и стандартов трубопроводов, которые можно использовать при анализе напряжений труб в зависимости от области применения (мощность, технологический химический процесс, распределение газа) и местоположения (страна или местная юрисдикция).Однако, чтобы не усложнять, это обсуждение основано на Американском обществе инженеров-механиков (ASME) B31.1 Power Piping. Физика анализа напряжений трубы не меняется в зависимости от кода трубопровода.

Анализ напряжений труб должен проводиться в первую очередь для обеспечения безопасности населения, проектируете ли вы систему отопления здания или газопровод высокого давления на нефтеперерабатывающем заводе. Общественная безопасность превыше всего. Первый принцип этического кодекса Национального общества профессиональных инженеров (NSPE) гласит: «Примите во внимание безопасность, здоровье и благополучие населения. ”

В хороший день поломка трубы — это всего лишь поломка опоры, о которой владелец не называет проектировщика / инженера. В плохой день владелец требует, чтобы проектировщик / инженер оплатил ущерб, а инженер предоставил решение бесплатно. В ужасный день кого-то убивают.

Еще одна причина, по которой выполняется анализ напряжений в трубах, — это увеличение срока службы труб. Большинство инженеров не считают кусок трубы оборудованием, но он ничем не отличается от насоса. Оба имеют движущиеся части и должны быть правильно спроектированы и обслуживаться для обеспечения надлежащего срока службы.Анализ напряжений труб также используется для защиты оборудования, потому что труба — это не что иное, как большое плечо рычага, соединенное с хрупким элементом оборудования. Если не поддерживать и не спроектировать должным образом, это может иметь разрушительные последствия для этого оборудования.

В дополнение к указанным выше, есть несколько общих причин, по которым может потребоваться анализ напряжений в трубе. В их числе:

• Повышенные температуры (> 250 ° F).
• Требуемое давление (300 фунтов на кв. Дюйм).
• Подключение чувствительного оборудования.
• Большое отношение D / t (> 50).
• Трубопровод, подверженный внешнему давлению.
• Критические услуги.

Ключевым моментом при выполнении анализа напряжений трубы является определение необходимого уровня детализации.

Как смоделировать трубопроводную систему

Компьютерные модели для анализа напряжений труб представляют собой серию трехмерных элементов балки, которые создают изображение геометрии трубопровода. Трехмерные балочные элементы являются наиболее эффективным способом моделирования трубопроводной системы, но не обязательно наиболее точным; а без сложных конечно-элементных моделей учесть все практически невозможно.Однако из исторического эмпирического тестирования известно, что эти методы и трехмерные компьютерные модели луча демонстрируют достаточно поведение, чтобы быть хорошим приближением.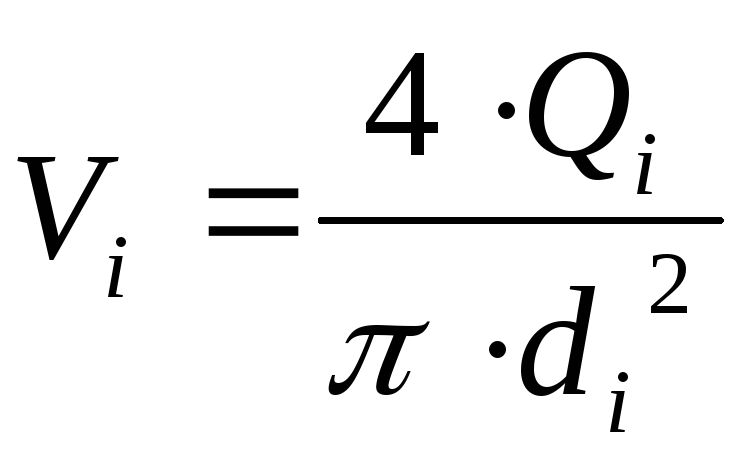 Кроме того, коды трубопроводов, такие как ASME B31, имеют запас прочности, допускающий приближение. При этом при моделировании трубопроводных систем есть некоторые подводные камни, которых следует избегать:

Качество моделей компьютеров зависит от введенной в них информации. При разработке анализа напряжений трубы, как и любой модели анализа методом конечных элементов (FEA), важно также понимать физику и граничные условия модели.

Элементы, используемые для моделирования системы трубопроводов, имеют свои ограничения. Одномерные балочные элементы отлично подходят для прямых отрезков трубопроводов, но не подходят для трубопроводной арматуры (колена, тройники, переходники и т. Д.). Поэтому ASME разработало коэффициенты усиления напряжения (SIF) для трубопроводной арматуры путем эмпирических испытаний. Они обеспечивают большее приближение без использования сложных моделей FEA с оболочками, плитами и кирпичными элементами.

Важно убедиться, что эти ограничения учтены при разработке анализа напряжений трубы. Большинство анализов напряжений в трубах не работают так, как мощный программный пакет FEA.

Элемент трехмерной балки

В поведении трехмерных элементов балки преобладают изгибающие моменты. Как упоминалось выше, он эффективен для большинства анализов и достаточен для системного анализа. Однако у использования трехмерного балочного элемента есть свои недостатки:

• На стенке трубы локальных эффектов не будет.
• Нет эффектов второго порядка.
• Нет большого вращения.
• Без учета большой сдвигающей нагрузки.
  • Прогиб стенки происходит до разрушения при изгибе.
  • Короткая, толстая консоль в сравнении с длинной и тощей.
• Эффекты оболочки / стены не видны.

Основные виды напряжений в трубопроводе

Существует пять основных напряжений в трубопроводе, которые могут вызвать отказ в системе трубопроводов: кольцевое напряжение, осевое напряжение, изгибающее напряжение, скручивающее напряжение и усталостное напряжение.

Кольцевое напряжение — это результат приложения давления к трубе изнутри или снаружи.Поскольку давление равномерно применяется к системе трубопроводов, кольцевое напряжение также считается равномерным по всей длине трубы. Обратите внимание, что кольцевое напряжение будет меняться в зависимости от диаметра и толщины стенки во всей трубопроводной системе. Напряжение кольца чаще всего выражается следующей формулой:

Осевого стресс результатов сдержанных осевой роста трубы. Осевой рост вызывается тепловым расширением, расширением под давлением и приложенными силами. Если участок трубы может свободно расти в одном направлении, то осевого нет — по крайней мере, теоретически.При сравнении осевого роста, вызванного давлением, рост стальной трубы минимален на высоте более 100 футов, и его можно не учитывать. Композитные трубопроводы, такие как трубы, армированные волокном (FRP) или пластиковые трубы, будут демонстрировать заметный рост на 2–3 дюйма на 100 футов при правильных условиях (200–300 фунтов на кв. Дюйм). Основная причина разницы в скорости роста под давлением связана с модулем упругости. Сталь имеет модуль упругости примерно 30 x 106 фунтов на квадратный дюйм, тогда как композиты будут иметь величину от 2 до 3 порядков или меньше.Осевое напряжение представлено осевой силой по площади поперечного сечения трубы:

Напряжение изгиба — это напряжение, вызванное физическими силами, приложенными к трубопроводу. К основным силам относятся труба и средний вес, сосредоточенные массы (клапаны, фланцы), случайные силы (сейсмические, ветровые, осевые нагрузки) и вынужденные смещения, вызванные ростом от соседних трубопроводов и соединений оборудования. Силы тела создают результирующий момент вокруг трубы, для которого напряжение может быть представлено моментом, разделенным на модуль упругости сечения:

Напряжение кручения — это результирующее напряжение, вызванное вращающим моментом вокруг оси трубы и вызванное массовыми силами.Однако, поскольку система трубопроводов, скорее всего, выйдет из строя при изгибе перед скручиванием, большинство нормативов по трубопроводам игнорируют эффекты кручения.

Усталостное напряжение создается путем непрерывного циклического изменения напряжений, присутствующих в трубопроводе. Например, включение и выключение водопроводного крана в течение всего дня приведет к усталостному стрессу, хотя и небольшому, из-за того, что давление сбрасывается, а затем увеличивается. В приложениях с силовым циклом циклическое изменение паровой турбины от низкого до высокого давления / температуры создает усталостное напряжение.Усталостное напряжение приводит к снижению допустимой прочности в системе трубопроводов и обычно вызвано циклическим воздействием:

• Давление.
• Температура.
• Вибрация, поток, вызванный или вызванный вращающимся оборудованием.
• Случайные нагрузки (легкий ветерок привел к обрушению моста Tacoma Narrows Bridge в штате Вашингтон от усталости).

Допустимые кодовые напряжения

Коды

для трубопроводов, например, опубликованные ASME, обеспечивают допустимое напряжение кода, которое представляет собой максимальное напряжение, которое трубопроводная система может выдержать до отказа кода.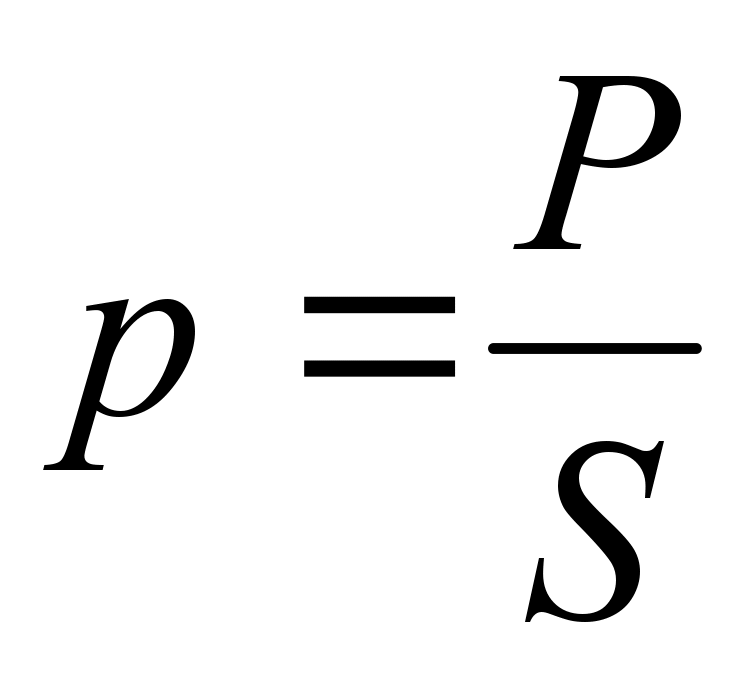 Ошибка кода не обязательно является неисправностью трубопровода. Это связано с факторами безопасности, заложенными в правилах трубопроводов. В кодексах ASME рассматриваются три различных типа напряжения: длительное напряжение, напряжение смещения (тепловое или расширяющееся) и случайное напряжение.

Устойчивое или продольное напряжение создается путем приложения нагрузок, необходимых для соблюдения законов равновесия между внешними и внутренними силами. Устойчивые стрессы не являются самоограничивающими. Если выдерживаемое напряжение превышает предел текучести материала трубопровода по всей толщине, предотвращение разрушения полностью зависит от деформационных свойств материала.

Напряжение смещения возникает из-за самостопорения конструкции трубопровода. Он должен удовлетворять установленной схеме деформации, а не находиться в равновесии с внешней нагрузкой. Напряжения смещения чаще всего связаны с воздействием температуры; однако внешние смещения, такие как осадки зданий, считаются напряжением смещения.

Случайное напряжение — это «сумма продольных напряжений, создаваемых внутренним давлением, временными и статическими нагрузками, а также возникающих при случайных нагрузках» согласно ASME B31.1, пункт 102.3.3 (A). Случайные напряжения могут превышать допустимое кодовое напряжение на определенный процент в зависимости от частоты и продолжительности нагрузки; для кодов трубопровода ASME это обычно 15% или 20%. Например, ветровые нагрузки могут превышать допустимое кодовое напряжение только на 15% из-за их частоты, а сейсмические нагрузки могут превышать на 20% из-за относительной редкости нагрузок.

Основы расчета давления

Как специалисту по анализу напряжений в трубе, очень важно понимать, как определяется толщина стенки.Если стенка трубы слишком тонкая, не имеет значения, как труба поддерживается; это не удастся. Обычно инженер, проектирующий систему, также определяет толщину стенки; однако толщина стенки также проверяется во время анализа напряжений трубы. Большинство инженеров больше озабочены массовым расходом и перепадом давления, поэтому влияние размера трубы и толщины стенки на них может быть потеряно. Переход на более толстую стенку трубы или больший размер трубы может окупить материальные затраты по сравнению с проблемами проектирования и дополнительными затратами на поддержку труб в рабочей силе и материалах.

Напряжение кольца (упрощенно) равно PDo4tn. Коды ASME применяют коэффициент безопасности два при определении толщины стенки на основе кольцевого напряжения, что дает:

.

Коэффициент запаса прочности должен учитывать дополнительные напряжения, вызванные изгибающими и осевыми напряжениями, которые будут применяться позже. Посредством основных алгебраических манипуляций кодовое уравнение для толщины стенки составляет:

A — это дополнительная толщина, добавленная к коррозии, эрозии и износу трубы во время нормальной эксплуатации.Значение A остается на усмотрение разработчика в ASME. Однако большинство людей считают 0,0625 дюйма приемлемым значением.

Минимальная (фактическая) толщина, указанная выше, основана на внутреннем диаметре (ID) трубопровода. Основное различие в двух уравнениях толщины стенки заключается в том, что упрощенная версия более консервативна, быстрее и проще рассчитывается для запланированных труб. Актуальная версия ближе к измеренному кольцевому напряжению. Большинство программ анализа напряжения по умолчанию рассчитывают ID на основе кольцевого напряжения.

Наконец, коды ASME требуют, чтобы минимальная толщина учитывала допуск фрезерования 12,5%:

Обратите внимание, что при факторинге допуска фрезерования 12,5% умножение на 1,125 не то же самое, что деление на 0,875.

Постоянные напряжения

Для тех, кто плохо знаком с анализом напряжений в трубах — нет причин, по которым устойчивые напряжения в трубе должны превышать 55% от стандартного допустимого напряжения. На то есть несколько причин. Во-первых, рекомендуемые пролеты опор труб регулируются прогибом, а не допустимым напряжением, чтобы обеспечить надлежащий поток и дренаж. Второй вывод из обсуждения выше, толщина стенки основана на коэффициенте безопасности, равном двум, который исключен из уравнения выдерживаемых напряжений.

Общество стандартизации производителей (MSS) SP-58: Подвески и опоры для труб — материалы, конструкция, изготовление, выбор, применение и установка рекомендует использовать пролет опор на основе критерия прогиба приблизительно 0.125 дюймов или меньше между опорами. Критерии отклонения предполагают балку с простой опорой. Однако система труб с опорой представляет собой балку с непрерывной опорой, которая уменьшает реакцию и моменты на каждой опоре, дополнительно уменьшая прогиб между опорами. Это сводит на нет изгибающие моменты между опорами и снижает изгибающий момент выдерживаемого напряжения.

Ниже приведено устойчивое уравнение из ASME B31.1:

Упрощенный член кольцевого напряжения в приведенном выше уравнении основан на минимальной толщине стенки и составляет приблизительно 50% допустимого напряжения, исходя из коэффициента безопасности толщины стенки. Однако в приведенном выше уравнении кольцевое напряжение основано на номинальной толщине стенки, которая, по крайней мере, в 1 / 0,875 раза больше минимальной толщины стенки. И наоборот, если кольцевое напряжение как функция минимальной толщины стенки составляет 50% допустимого кодового напряжения, то кольцевое напряжение как функция номинальной толщины стенки составляет 50% x 0,875 = 43,75%.

Как упоминалось выше, уравнение выдерживаемого напряжения основано на номинальной толщине стенки с дополнительной толщиной стенки для фрезерования и коррозии. Из-за дополнительной толщины стенки труба имеет дополнительную прочность, чтобы противостоять прогибу.Кроме того, чтобы добиться разрушения трубы из-за прогиба, поддерживаемые пролеты трубы должны быть по крайней мере в три-четыре раза больше по длине, чем рекомендованные пролеты MSS SP-58. Момент из-за собственного веса вносит примерно 10% кодового напряжения в приведенное выше уравнение при использовании рекомендованных MSS SP-58 пролетов для опор труб.

Оглядываясь назад на приведенное выше уравнение устойчивого напряжения, если вы предположите, что кодовое напряжение составляет 10% от мертвых моментов, а 44% — кодовое напряжение от кольцевого напряжения, то устойчивое напряжение должно быть примерно 54% ​​или меньше.Если это не так, обычно наблюдаются чрезмерные прогибы на изгибе и / или сосредоточенная масса в трубопроводе, что создает более высокий, чем ожидалось, изгибающий момент от несбалансированной системы (см. Таблицу 2).

Рекомендации по стандартному диапазону

Ниже приведены некоторые общие соображения по поводу стандартных пролетов труб, которые следует учитывать:

• Жидкость оказывает большее влияние по мере увеличения размера трубы. Вес воды превышает вес трубы для номинального размера трубы 12 дюймов (NPS) для стандартной толщины стенки (STD) или больше.
• При наличии сосредоточенных нагрузок, таких как фланцы, клапаны и специальные элементы трубопроводов между опорами труб, рекомендуемый пролет должен быть уменьшен для их учета.
• Опора трубы должна быть размещена в пределах одной трети рекомендованного пролета соединения вращающегося оборудования, чтобы минимизировать вертикальную нагрузку и моменты при соединении. В большинстве случаев эта опора должна быть переменной пружиной, чтобы помочь с регулировкой и уменьшить поступательную вибрацию.
• При изменении горизонтального направления трубопровода рекомендуемый интервал между опорами труб должен быть уменьшен на 25%.

Напряжения смещения

В большинстве случаев, если считается, что напряжения смещения или расширения вызывают беспокойство (например, повышенные температуры), то требуется компьютерный анализ напряжений трубы. Если выполняется компьютеризированный анализ, напряжения смещения должны поддерживаться на уровне от 80% до 90% от того, что позволяет код.

Как правило, эта рекомендация выполняется путем обеспечения того, чтобы нагрузки подключения оборудования находились в пределах опубликованных допустимых нормативных напряжений, за счет добавления гибкости к системе трубопроводов. Системы гибких трубопроводов обычно имеют низкие смещающие напряжения, поскольку трубопровод может свободно расти.

Случайные напряжения

Случайные напряжения в системе трубопроводов вызываются кратковременными событиями, такими как сейсмические, ветровые и осевые нагрузки. Эти три нагрузки составляют большинство возможных случайных комбинаций нагрузок. Поскольку случайные напряжения носят кратковременный характер, большинство норм по трубопроводам допускают повышенные напряжения труб на короткий период. Коды ASME обычно допускают увеличение:

• Пятнадцать процентов, если мероприятие длится менее 8 часов и не более 800 часов в год
• Двадцать процентов, если мероприятие длится менее 1 часа и не более 80 часов в год.

Как правило, ветровые нагрузки подпадают под категорию увеличения на 15%, в то время как сейсмические и рельефные нагрузки увеличиваются на 20%.

Если случайные напряжения считаются проблемой или носят сложный характер, необходим компьютеризированный анализ напряжений в трубах.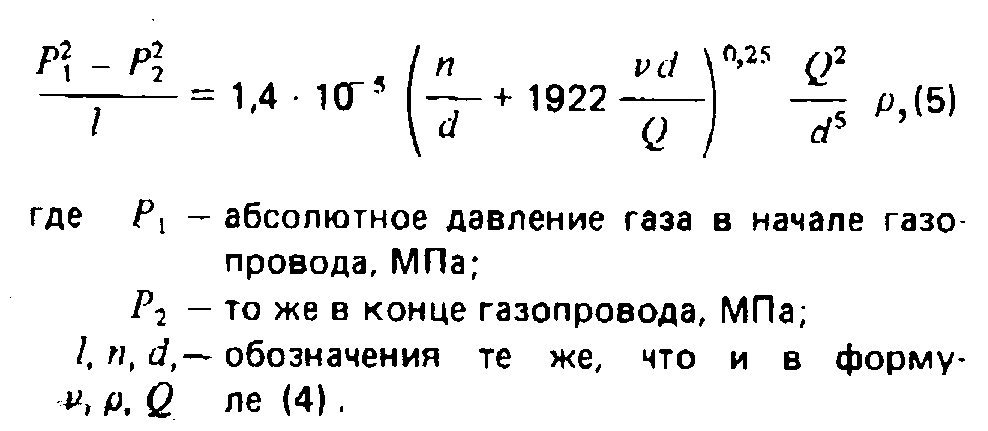 Однако в большинстве случаев. добавление боковых ограничителей для каждых трех или четырех номинальных пролетов опор труб будет покрывать большинство сейсмических или ветровых нагрузок, если только они не находятся в зоне с высокой сейсмичностью, такой как Калифорния, или подвергаются прибрежной ветровой нагрузке с устойчивыми ураганными ветрами.

Ведение записей анализа труб

Большинство людей считают, что компьютерная распечатка является достаточной записью анализа напряжений трубы. Это большая ошибка, которую можно избежать, приложив немного усилий. Создание записи о вашей работе — это больше, чем просто сохранение бумажной копии или PDF-файла компьютерного анализа напряжений трубы. Это означает документирование всех входных данных, а не только чертежей, используемых для создания геометрии трубопроводов. Элементы, которые могут быть включены, включают схемы трубопроводов и приборов, параметры системы, случаи нагружения и любые соответствующие внешние силы, приложенные к системе трубопроводов, местоположения опор труб и тип используемых опор труб. Большинство записей анализа напряжений трубы заполняют связку с тремя кольцами.

Поскольку большинство инженеров-консультантов имеют внутренние процедуры обеспечения качества / контроля качества, разработайте стандартный список обычно используемых входных данных и соответствующие ссылки для информации. Это предоставит контролеру вычислений место, где можно подписаться, указав, что они согласны с вводными данными и подтверждают источник ввода. В конце концов, ваша документация должна рассказывать полную историю.

---

Monte Engelkemier — руководитель группы инженеров по трубопроводам, механике и оборудованию в подразделении крахмалов, подсластителей и текстуризаторов компании Cargill.До этого он в течение 12 лет был членом Stanley Consultants, где написал эту статью, прежде чем занять свою нынешнюю должность.

Потери в трубах

На этой странице представлен краткий обзор потерь в трубопроводе, начиная с уравнения Бернулли

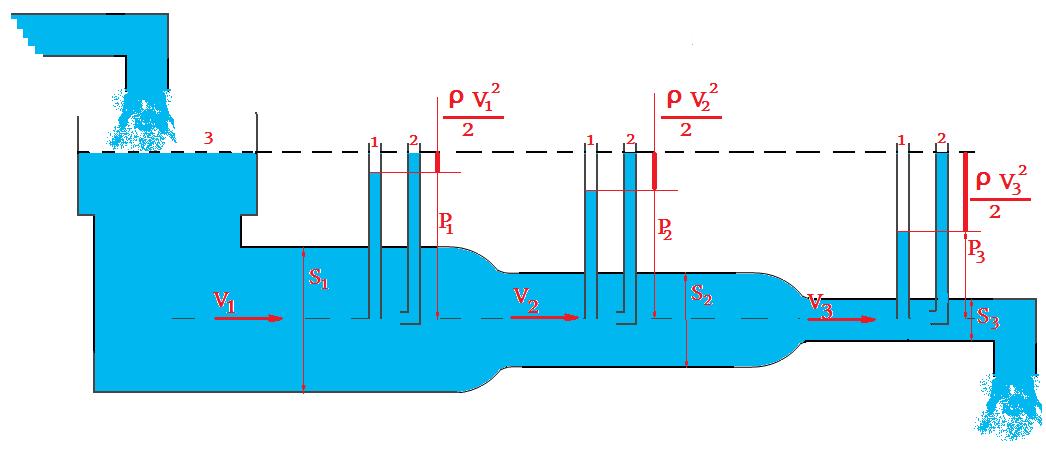
Основной подход ко всем системам трубопроводов состоит в том, чтобы записать уравнение Бернулли между двумя точками, соединенными линией тока, где условия известны. Например, между поверхностью резервуара и выходом трубы.

Общий напор в точке 0 должен совпадать с общим напором в точке 1 с поправкой на любое увеличение напора из-за насосов, потерь из-за трения трубы и так называемых «малых потерь» из-за входов, выходов, фитингов и т. Д. Напор насоса обычно зависит от расхода в системе, при этом подъем напора уменьшается с увеличением расхода через насос.

Потери на трение в трубах

Потери на трение являются сложной функцией геометрии системы, свойств жидкости и скорости потока в системе.По наблюдениям, потеря напора примерно пропорциональна квадрату расхода в большинстве инженерных потоков (полностью развитый турбулентный поток в трубе). Это наблюдение приводит к уравнению Дарси-Вейсбаха для потери напора из-за трения:

, который определяет коэффициент трения f. f нечувствителен к умеренным изменениям потока и постоянен для полностью турбулентного потока. Таким образом, часто бывает полезно оценить взаимосвязь, поскольку напор прямо пропорционален квадрату расхода для упрощения расчетов.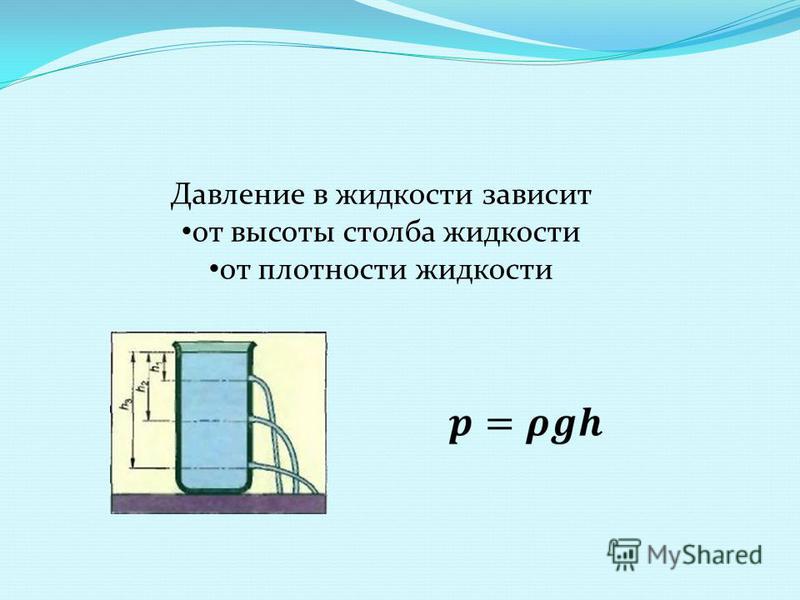

Число Рейнольдса — это фундаментальная безразмерная группа в вязком потоке. Скорость, умноженная на шкалу длины, деленная на кинематическую вязкость.

Относительная шероховатость связывает высоту типичного элемента шероховатости с масштабом потока, представленным диаметром трубы D.

Поперечное сечение трубы важно, поскольку отклонения от круглого поперечного сечения вызовут вторичные потоки, которые увеличивают падение давления. Некруглые трубы и воздуховоды обычно обрабатываются с использованием гидравлического диаметра

.

вместо диаметра и трактует трубу как круглую.

Для ламинарного потока потеря напора пропорциональна скорости, а не квадрату скорости, поэтому коэффициент трения обратно пропорционален скорости.

Коэффициент геометрии k
Квадрат	56,91
2: 1 прямоугольник	62,19
5: 1 прямоугольник	76,28
Параллельные пластины	96. 00

Число Рейнольдса должно основываться на гидравлическом диаметре. Blevins (Справочник по прикладной гидродинамике, таблица 6-2, стр. 43-48) приводит значения k для различных форм. Для турбулентного потока Коулбрук (1939) обнаружил неявную корреляцию для коэффициента трения в круглых трубах. Эта корреляция хорошо сходится за несколько итераций. Сходимость можно оптимизировать за счет небольшого недостаточного расслабления.

Знакомая диаграмма Муди представляет собой логарифмический график корреляции Коулбрука по осям коэффициента трения и числа Рейнольдса в сочетании с результатом f = 64 / Re для ламинарного потока.

Явное приближение

обеспечивает значения в пределах одного процента от Colebrook в большей части полезного диапазона.

Расчет потери напора для известного расхода

По Q и трубопроводу определяют число Рейнольдса, относительную шероховатость и, следовательно, коэффициент трения. Подставляем в уравнение Дарси-Вайсбаха, чтобы получить потерю напора для данного расхода. Подставьте в уравнение Бернулли, чтобы найти необходимую высоту или напор насоса.

Расчет расхода для известного напора

Получите допустимую потерю напора из уравнения Бернулли, затем начните с определения коэффициента трения.(0,02 — хорошее предположение, если у вас нет ничего лучше.) Рассчитайте скорость по уравнению Дарси-Вайсбаха. Исходя из этой скорости и характеристик трубопровода, рассчитайте число Рейнольдса, относительную шероховатость и, следовательно, коэффициент трения.

Повторяйте расчет с новым коэффициентом трения до тех пор, пока не будет достигнута достаточная сходимость. Q = VA.

Вот видео, в котором обсуждаются три типа проблем трубопроводов:

«Мелкие убытки»

Хотя они часто составляют основную часть потерь напора, особенно в технологических трубопроводах, дополнительные потери из-за входов и выходов, фитингов и клапанов традиционно называют незначительными потерями. Эти потери представляют собой дополнительную диссипацию энергии в потоке, обычно вызываемую вторичными потоками, вызванными кривизной или рециркуляцией. Незначительные потери представляют собой любую имеющуюся потерю напора в дополнение к потере напора для той же длины прямой трубы.

Как и трение в трубе, эти потери примерно пропорциональны квадрату расхода. Определив K, коэффициент потерь, на

позволяет легко интегрировать небольшие потери в уравнение Дарси-Вейсбаха.K — это сумма всех коэффициентов потерь на длине трубы, каждый из которых вносит свой вклад в общую потерю напора.

Хотя K кажется постоянным коэффициентом, он меняется в зависимости от условий потока. Факторы, влияющие на значение K, включают:

• точная геометрия рассматриваемого компонента
• поток Число Рейнольдса
• близость к другим фитингам и т. Д. (Значения K в таблице приведены для отдельных компонентов — с длинными прямыми участками трубы до и после.