Формула простого процентного роста: Урок математики в 6-м классе на тему «Решение задач на процентный рост»

Дек 22 2020

alexxlab

План-конспект урока по алгебре (6 класс) по теме: открытый урок в 6 классе по теме «Процентный рост»

ПЛАН-КОНСПЕКТ УРОКА

1. ФИО

2. Место работы

3. Должность

4. Предмет

5. Класс

6. Тема и номер урока в теме

7. Базовый учебник

Богатырёва Анна Константиновна

МАОУ «СОШ №42»

учитель математики

математика

Решение задач на процентный рост (урок обобщения)

Математика 6, Петерсон

Дидактическая цель: применить изученный материал в знакомой и новой учебной ситуации.

Тип урока: Урок-практикум.

Цели по содержанию:

Образовательные: создать условия для формирования умений и навыков решения задач на простой и сложный процентный рост: а) тренировать способности к построению моделей текстовых задач с числовыми данными с помощью введения буквенных обозначений; б) формировать умения и навыки работы по формулам; продолжить формирование вычислительных навыков.

Развивающие: создать условия для развития учебно-интеллектуальных умений (анализ, сравнение, обобщение), коммуникативных умений.
Воспитательные: создать условия для формирования навыков самоконтроля и взаимоконтроля, рефлексии собственной деятельности, формирования личностного отношения к изучаемому материалу урока.

Структура урока:

Орг. момент.
Актуализация знаний.
Целеполагание и мотивация.
Применение знаний: а) в знакомой учебной ситуации; б) в новой учебной ситуации.
Рефлексия деятельности.
Домашнее задание.

Методы:

Репродуктивный.
Частично-поисковый.

Формы контроля: самоконтроль, взаимоконтроль, контроль учителя.

Формы организации деятельности: фронтальная, индивидуальная, работа в парах.

Ход урока

I. Орг. момент.

Здравствуйте! Проверьте своё рабочее место, всё ли готово у вас к уроку.
С каким настроением вы пришли на урок (прислушайтесь к себе)? (Ученики поднимают одну из карточек, выданную учителем перед началом урока, тем самым сигнализируют о своём настроении.)

К-1 (красного цвета)	К-2 (зелёного цвета)	К-3 (синего цвета)
Я готов к работе на уроке, занимаю активную жизненную позицию, хочу отвечать, спросите меня.	Я готов к работе на уроке, но не уверен в себе, для меня предпочтительнее работа в тетради и поменьше спрашивайте меня.	У меня сегодня какой то неудачный день, всё валится из рук, с утра нет никакого настроения. Я постараюсь включиться в работу, но не спрашивайте меня.

Я постараюсь учесть ваше настроение. Извините, если нарушу вашу установку!

У каждого из вас на столах лежат карточки самоконтроля. Подпишите их. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждой задачи, вы должны оценить свою работу:

«+» — справился с задачей без затруднений,

«±» — справился с задачей, но возникали сложности,

«-» — не справился с задачей.

2. Актуализация.

Прежде чем перейти непосредственно к решению задач, я хочу задать вам несколько вопросов, чтобы убедиться, что все ученики имеют представление о процентах, провести своего рода разминку.

У доски трое учеников

Обыкновенная дробь	½	¼	1/5	1/8	2/5	3/5	¾	4/5
Десятичная дробь
процент

1 ученик: Заполняет таблицу

2 ученик: Вычислить (работа с рисунком)

3 ученик: решает задачу

В городе N живёт 100000 жителей. Среди них 15% детей и подростков. Среди взрослых 45% не работает (пенсионеры, домохозяйки, безработные). Сколько взрослых работает? (46750)

Остальной класс выполняет математический диктант (1 человек с обратной стороны доски)

Задание, которое диктует учитель	Записи в тетрадях учащихся
325	325
Увеличить на 10	335
Округлить до десятков	340
Вычесть 34	306
Записать ближайшее следующее число, кратное 4	308
Найти 25%	77
Записать остаток от деления на 9	5
Увеличить на 50%	7,5
Прибавить треть числа	10
Это 25%	40

Молодцы! Отметили в листе самоконтроля.

Вспомним некоторые понятия: ПРЕЗЕНТАЦИЯ слайд 2

Молодцы! Отметили в листе самоконтроля.

Итак, сегодня у нас тема урока «Решение задач на процентный рост».

1. Что нам необходимо вспомнить, чтобы успешно справиться с заданиями?

Формулу простого процентного роста.(Sn = S(1+ pn/100))
Формулу сложного процентного роста.(Sn = S(1 + p/100)n.
Что обозначают входящие в формулы переменные?

Sn – итоговая сумма.

S – первоначальная сумма.

p – процентная ставка.

n — срок.

Проанализируйте формулы и сравните их: в чём сходство и различие?

III. Как вы думаете, для чего мы изучаем данный материал?

1. Темп жизни очень высок, идёт большой поток информации.

И чтобы не потеряться, идти в ногу со временем, конечно, надо уметь разбираться в различной информации, в том числе и с процентным ростом, тем более он встречается довольно часто. Где? Приведите примеры:

начисление банковских процентов;
начисление пени за несвоевременную плату;
амортизация оборудования и т.д.

2. Свяжите изучаемую тему с вашей будущей профессией. Помечтайте, кем вы хотите себя видеть в будущем и пригодиться ли вам изучаемый материал. Кто готов поделиться с нами своими мыслями?

3. Сегодня мы решаем сложные задачи, они встречаются на ЕГЭ.

Кто из вас собирается заканчивать 11-й класс? Тогда вам, в особенности, следует обратить серьёзное внимание на эти задачи. Чтобы быть конкурентно-способными при поступлении в учебные заведения, надо уметь решать задачи такого типа.

Итак, сформулируйте для себя цель урока. (Чему сегодня на уроке я могу научиться?). Запишите в тетрадь.

Учитель просит нескольких учеников зачитать, что они написали.

IV. Реклама.

1. Как в любом фильме на самом интересном месте бывает реклама, так и у нас на очереди – реклама!

Ученики за неделю получили задание: найти в газетах рекламу банков.

Сейчас зачитывают и сдают.

Два ученика получают задание: внести в таблицу на доске информацию о названии банка, вклада, процентной ставке, минимальной сумме вклада, сроке и видах процентов. (см. Приложение-2.)

2. Решаем задачу №1. (см. Приложение-1)

Поставьте себя на место актёра и сделайте предположение: какой из банков принёс больший доход? К доске приглашаются два человека: один решает задачу для случая, когда рассматриваются простые проценты, другой – сложные проценты. Все решают самостоятельно, затем проверяем, сравниваем и делаем вывод.

3. Работа с таблицей.

Сравните процентную ставку, минимальную сумму, срок, вид процентов.
Какой вклад вам кажется предпочтительнее?

4. Составьте задачу по таблице и решите её. Если испытываете затруднение, продолжите решение задач № 2, 3, 4 на выбор. (см. Приложение-1).

Через несколько минут учащиеся говорят о своём выборе и результатах.

5. Прошу обратить ваше внимание на задачу № 5. (см. Приложение-1).

Данная задача из ЕГЭ 2005 года.

Решаем задачу:

Заполните лист самоконтроля

V. Итак, наш урок подходит к концу. Давайте подведём итоги:

— изменился ли цвет вашей карточки? Если да, то как?

— достигли ли вы цели, поставленной в начале урока?

Сдайте листы самоконтроля

VI. Выберите для себя домашнее задание.

Дорешать задачи с листочка.

Или: выполнить творческую работу:

Найти в прессе рекламу какого – либо банка и составить задачу с интересным условием. Например: я стал профессиональным футболистом, заключил контракт с клубом «Арсенал» (Лондон) и получил гонорар 500000$. В каких банках выгоднее разместить данную сумму?

Или: написать мини сочинение на тему моя будущая профессия, для чего я изучаю проценты.

Содержание

Калькулятор онлайн — Найти число зная его процент

Этот калькулятор онлайн решает задачу на нахождение числа, зная его процент.

Онлайн калькулятор для нахождения числа по его процентам не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода чисел

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $ -\frac{2}{3} $

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: $ -1\frac{5}{7} $

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Сообщение отправлено. Спасибо.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или $ \frac{1}{100} $ часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:

$ 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 $

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

$ 0,58 = (0,58 \cdot 100)\% = 58\% $ $ 0,045 = (0,045 \cdot 100)\% = 4,5\% $

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти $ \frac{p}{100} $ от a, надо a умножить на $ \frac{p}{100} $:

$ b = a \cdot \frac{p}{100} $

Итак, чтобы найти р% от числа, надо это число умножить на дробь $ \frac{p}{100} $. Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью $ \frac{p}{100} , \; (p \neq 0) $, надо b разделить на $ \frac{p}{100} $:
$ a = b : \frac{p}{100} $

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на $ \frac{p}{100} $. Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а $ (a \neq 0) $, надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

$ p = \frac{b}{a} \cdot 100\% $ Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют $ \frac{9 \cdot 100}{180} = 5\% $ раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

$ b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) $ взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или $ \frac{pn}{100}S $, а всего придется заплатить $ S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S $
Таким образом:
$ S_n = \left( 1+ \frac{pn}{100} \right) S $

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
$ S_n = \left( 1- \frac{pn}{100} \right) S $

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет $ \frac{p}{100}S $ р., и через год на счете окажется сумма
$ S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S $
то есть начальная сумма увеличится в $ 1+ \frac{p}{100} $ раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
$ S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S $

Аналогично $ S_3 = \left( 1+ \frac{p}{100} \right)^3 S $ и т.д. Другими словами, справедливо равенство
$ S_n = \left( 1+ \frac{p}{100} \right)^n S $

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Калькулятор онлайн — Найти сколько процентов составляет одно число от другого

Этот калькулятор онлайн решает задачу на нахождение процентного соотношения между двумя числами.

Онлайн калькулятор для нахождения процентного соотношения между двумя числами не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода чисел

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $ -\frac{2}{3} $

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: $ -1\frac{5}{7} $

Сообщение отправлено. Спасибо.

Понятие о проценте

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:

$ 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 $

$ 0,58 = (0,58 \cdot 100)\% = 58\% $ $ 0,045 = (0,045 \cdot 100)\% = 4,5\% $

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

1. Нахождение процента от числа.
Чтобы найти $ \frac{p}{100} $ от a, надо a умножить на $ \frac{p}{100} $:

$ b = a \cdot \frac{p}{100} $

Нетрудно заметить, что формулы

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Сложный процентный рост

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Аналогично $ S_3 = \left( 1+ \frac{p}{100} \right)^3 S $ и т.д. Другими словами, справедливо равенство
$ S_n = \left( 1+ \frac{p}{100} \right)^n S $

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Формула темпа роста в процентах и примеры

Понятие показателя темпа роста

Показатель темпа роста может измеряться в процентах или в относительных значениях.

Темп экономического роста напрямую зависит от типа экономического роста. В экономике выделяют два 2 типа экономического роста:

Экстенсивный тип роста, при которомрост объема производства происходит благодаря внедрению определенного, большого числа факторов (сырья, топлива, рабочей силы, оборудования и др.).
Интенсивный тип роста увеличивает производственный объем за счет совершенствования качественных показателей (квалификации, технологий, достижений научно-технического прогресса). При данном типе роста изменения происходят посредством улучшения качества, а не количества.

Если в экономике происходит интенсивный тип роста, то темпы могут даже немного снижаться, если сравнивать его с экстенсивным типом. Тем не менее, это не свидетельствует о спаде экономического развития или то, что оно замедляется.

Существует несколько особенностей типов роста:

В случае экстенсивного типа роста экономика может сохранить пропорции, свои структурные характеристики, при этом продолжить развитие вширь.
В процессе интенсивного типа роста экономика может стать динамичной благодаря расширению производства, а также по причине прогрессивных структурных перестроек.

Формула темпа роста в процентах

В общем виде формула темпа роста в процентах выглядит следующим образом:

Тр=Pнп/Pкп

Здесь Тр –показатель темпа роста,

Рнп – показатель на начало периода,

Ркп – показатель на конец периода.

Для того, что бы получить более наглядный результат, полученное значение принято умножать на 100%, что бы выразить формулу темпа роста в процентах.

Значения темпа роста

Темп роста отражает динамику, на сколько процентов изменяется (растет) статистический показатель текущего периода при сравнении его со значением предыдущего периода.

Если использовать различные значения формулы, то можно увидеть 3 варианта динамики значений:

1) Если темп роста больше 100%, то можно наблюдать положительную динамику.

2) Темп роста = 100% не означает никаких изменений.

3) Темп роста меньше 100% свидетельствует об отрицательной динамике.

Темп роста и темп прироста

Часто происходит путаница при определении понятий темпа роста и прироста, так как их формулы легко спутать.

Для того, что бы определить темпа прироста из показателей расчетного периода вычитают показатель базового периода, впоследствии это результат делят на показатель базисного периода и умножают на 100%. В итоге мы получаем значение темпа прироста в процентах.

Для того, чтобы не происходила путаница в этих понятиях, можно отметить, что темп роста показывает увеличение самого показателя, то есть во сколько раз он изменился в определенном временном промежутке.

Темп прироста же показывает, насколько выросло значение показателя за этот период времени (сравнение).

Примеры решения задач

Формула темпа прироста и примеры применения

Понятие и значение темпа прироста

Темп прироста используется при анализе какого-либо ряда динамики. Формула темпа прироста часто применяется в статистике и экономике в паре с таким показателем, как темп роста (в процентном соотношении).

Если в результате расчета получается положительная величина, то можно говорить об увеличивающемся темпе прироста, при отрицательном же значении происходит снижение темпа исследуемого значения, если сравнивать его с предыдущим (базисным) периодом.

Формула темпа прироста часто применяется в анализе инвестиционных проектов. Также этот показатель часто используется муниципальными организациями при расчетах:

вычисление прироста населения;
будущей потребности в зданиях;
объемов оказания услуг и др.

Формула темпа прироста

Для расчета темпа прироста нужно найти отношение исследуемого показателя к предыдущему (базисному), далее из получаемого результата вычесть единицу. Окончательный результат умножается на 100, для того, что бы выразить итог в процентах. Формула темпа прироста по первому способу выглядит так:

Тп=((Пип/Пбп)-1)*100%

Здесь Тп – темп прироста,

Пбп – показатель базисного периода,

Пип – показатель исследуемого периода.

В случае, когда вместо фактического значения анализируемых показателей известно только значение абсолютного прироста, применяют альтернативную формулу. При этом находят процентное отношение абсолютного прироста к тому уровню, в сравнении с которым он и рассчитывался.

Тп=((Пип-Пбп)/Пбп)*100%

Здесь Тп – темп прироста,

Пбп – показатель базисного периода,

Пип – показатель исследуемого периода.

Отличие темпа роста и темпа прироста

Большую сложность для учащихся представляет отличие темпа роста от темпа прироста. Выделим несколько положений, в которых заключается разница между этими величинами:

Формула темпа роста и формула темпа прироста рассчитываются по разным методикам.
Темп роста отражает количество процентов одного показателя относительно другого, а темп прироста показывает, насколько он вырос.
На основании расчетов по формуле темпа роста можно рассчитать темп прироста, при этом по формуле темпа прироста расчет темпа роста не проводят.
Темп роста не принимает отрицательное значение, при этом темп прироста может получаться как положительной, так и отрицательной величиной.

Примеры решения задач

Как рассчитать процент в Excel — примеры формул процента

В этом учебном пособии вы узнаете, как быстро рассчитать проценты в Excel, найти базовую формулу процентного соотношения и еще несколько формул для расчета процентного увеличения, общего процента и т. Д.

Расчет процента полезен во многих сферах жизни, будь то чаевые в ресторанах, комиссия реселлера, ваш подоходный налог или процентная ставка. Скажем, вам повезло получить скидочный код 25% на новый плазменный телевизор.Это хорошая сделка? И сколько вам в конечном итоге придется заплатить?

В этом руководстве мы рассмотрим несколько методов, которые помогут вам эффективно рассчитать процент в Excel, а также изучат базовые формулы процента, которые помогут угадать ваши расчеты.

Процент основы

Термин «процент» происходит от латинского процента , что означает «на сто». Как вы, наверное, помните из математического урока в старшей школе, процент — это доля от 100, которая рассчитывается путем деления числителя на знаменатель и умножения результата на 100.

Основная процентная формула выглядит следующим образом:

(часть / вся) * 100 = процент

Например, если у вас было 20 яблок и вы дали 5 своим друзьям, сколько вы дали, в процентном отношении? Выполнив простой расчет = 5/20 * 100 , вы получите ответ — 25%.

Так вы обычно рассчитываете проценты в школе и в повседневной жизни. Вычислить процент в Microsoft Excel еще проще, поскольку Excel выполняет некоторые операции автоматически в фоновом режиме.

К сожалению, не существует универсальной формулы Excel для процента, которая охватывала бы все возможные сценарии. Если вы спросите кого-нибудь «Какой процентный показатель я использую, чтобы получить желаемый результат?», Скорее всего, вы получите ответ типа «Ну, это зависит от того, какого именно результата вы хотите достичь».

Итак, позвольте мне показать вам несколько простых формул для расчета процентов в Excel, таких как формула процентного увеличения, формула для получения процентов от общей суммы и многое другое.

Basic Excel, процентная формула

Основная формула для расчета процента в Excel:

Часть / Итого = Процент

Если вы сравните ее с базовой математической формулой для процентов, вы заметите, что в формуле процентов для Excel отсутствует часть * 100.При вычислении процента в Excel нет необходимости умножать полученную дробь на 100, поскольку Excel делает это автоматически, когда формат процента применяется к ячейке.

А теперь давайте посмотрим, как вы можете использовать формулу процента Excel для реальных данных. Предположим, у вас есть число « Заказанные позиции » в столбце B и « Поставленных товаров » в столбце C. Чтобы узнать процент поставленных продуктов, выполните следующие шаги:

Введите формулу = C2 / B2 в ячейку D2 и скопируйте ее в столько строк, сколько вам нужно.
Нажмите кнопку Percent Style (вкладка Главная > группа Номер ), чтобы отобразить полученные десятичные дроби в процентах.
Не забывайте увеличивать количество знаков после запятой, если это необходимо, как описано в советах по процентам.
Готово! 🙂

Такая же последовательность шагов должна выполняться при использовании любой другой процентной формулы в Excel.

В следующем примере столбец D отображает округленный процент доставленных товаров без отображения десятичных знаков.

Расчет процента от суммы в Excel

Фактически, вышеприведенный пример является частным случаем вычисления процентов от общей суммы. Теперь давайте рассмотрим еще несколько примеров, которые помогут вам быстро рассчитать процент от общей суммы в Excel для разных наборов данных.

Пример 1. Сумма находится в конце таблицы в определенной ячейке

Очень распространенный сценарий, когда у вас есть итог в одной ячейке в конце таблицы. В этом случае процентная формула будет аналогична той, что мы только что обсуждали, с той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной (с $).Знак доллара фиксирует ссылку на данную ячейку, так что она никогда не изменяется независимо от того, куда скопирована формула.

Например, если у вас есть некоторые значения в столбце B и их итоговые значения в ячейке B10, вы будете использовать следующую формулу для расчета процентов от общей суммы: = B2 / $ B $ 10

Вы используете относительную ссылку на ячейку B2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца B. Но вы вводите $ B $ 10 в качестве абсолютной ссылки на ячейку, потому что вы хотите оставить знаменатель фиксированным на B10 при автоматическом заполнении формулы до строки 9.

Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.

На приведенном ниже снимке экрана показаны результаты, возвращаемые по формуле. Столбец Процент от общего количества отформатирован в процентах с отображением 2 десятичных знаков.

Пример 2. Части итога находятся в несколько рядов

В приведенном выше примере предположим, что у вас есть несколько строк для одного и того же продукта, и вы хотите знать, какую часть итога составляют все заказы этого конкретного продукта.

В этом случае вы можете использовать функцию SUMIF, чтобы сначала сложить все числа, относящиеся к данному продукту, а затем разделить это число на сумму, например:

= SUMIF (диапазон, критерии, сумма_диапазон) / всего

Учитывая, что в столбце A содержатся все названия продуктов, в столбце B перечислены соответствующие количества, ячейка E1 — это название продукта, который вас интересует, а итог находится в ячейке B10, ваша реальная формула может выглядеть примерно так:

= SUMIF (A2: A9, E1, B2: B9) / $ B $ 10

Естественно, вы можете указать название продукта непосредственно в формуле, например:

= SUMIF (A2: A9, "вишня", B2: B9) / $ B 10

Если вы хотите узнать, какую часть общего количества составляют несколько различных продуктов, сложите результаты, возвращенные несколькими функциями SUMIF, а затем разделите это число на общее количество.Например, следующая формула рассчитывает процент вишни и яблок:

= (SUMIF (A2: A9, «вишня», B2: B9) + SUMIF (A2: A9, «яблоки», B2: B9)) / $ B 10

Для получения дополнительной информации о функции SUM, пожалуйста, ознакомьтесь со следующими уроками:

Как рассчитать процентное изменение в Excel

Из всех формул для расчета процента в Excel, формула процентного изменения, вероятно, является той, которую вы будете использовать чаще всего.

Формула Excel для процентного изменения (процентное увеличение / уменьшение)

Чтобы рассчитать процентное изменение между значениями A и B, используйте следующую формулу:

Процентное изменение = (B — A) / A

При применении этой формулы к реальным данным важно правильно определить, какое значение равно A, а какое — B.Например, вчера у вас было 80 яблок и то, что у вас есть 100, то есть теперь у вас на 20 яблок больше, чем раньше, что на 25% больше. Если у вас было 100 яблок, а теперь у вас 80, количество яблок уменьшилось на 20, что на 20% меньше.

Учитывая вышеизложенное, наша формула Excel для процентного изменения принимает следующую форму:

(новое значение — старое значение) / старое значение

А теперь давайте посмотрим, как вы можете использовать эту формулу процентного изменения (формула процентного увеличения Excel) в своих электронных таблицах.

Пример 1. Расчет процентного изменения между 2 столбцами

Предположим, у вас есть цены за последний месяц в столбце B и цены за этот месяц в столбце C. Затем вы можете ввести следующую формулу в ячейку D2, чтобы рассчитать процентное изменение в листе Excel:

= (C2-B2) / B2

Эта формула процентного изменения вычисляет процентное увеличение / уменьшение в этом месяце (столбец C) по сравнению с прошлым месяцем (столбец B).

После копирования формулы в другие строки, не забудьте нажать кнопку Percent Style на ленте, чтобы отобразить десятичные дроби в процентах, и вы получите результат, подобный тому, что вы видите на скриншоте ниже.В этом примере положительные проценты, которые показывают процентное увеличение, отформатированы в обычном черном цвете, в то время как отрицательные проценты (процентное уменьшение) отформатированы красным, используя методику, описанную в этом совете.

Пример 2. Расчет процентного изменения между строками

Если у вас есть один столбец чисел, например, столбец C, в котором перечислены недельные или ежемесячные продажи, вы можете рассчитать процентное изменение по следующей формуле:

= (C3-C2) / C2

Где C2 — это 1 ^-й, а C3 — это 2 ^{-й и}-й элемент с данными.

Примечание. Обратите внимание, что вам следует пропустить первую строку с данными и поместить формулу процентного соотношения Excel в ячейку 2 ^и, в данном примере D3.

После применения формата процента к столбцу с формулой изменения процента вы получите следующий результат:

Если вы хотите рассчитать процентное изменение по сравнению с определенной ячейкой, то вам нужно исправить ссылку на эту ячейку, используя абсолютную ссылку на ячейку со знаком $, e.грамм. $ C $ 2.

Например, вот формула процентного изменения Excel, которая рассчитывает процентное увеличение / уменьшение для каждого месяца по сравнению с январем (C2):

= (C3- $ C $ 2) / $ C $ 2

При перетаскивании формулы вниз для ее копирования в другие ячейки абсолютная ссылка ($ C $ 2) останется прежней, а относительная ссылка (C3) изменится на C4, C5 и т. Д.

Расчет суммы и суммы в процентах

Как вы только что видели, рассчитать проценты в Excel легко, как и подсчет сумм и итогов, если вы знаете процент.

Пример 1. Рассчитать сумму по сумме и процентам

Предположим, вы покупаете новый ноутбук за 950 долларов, и с этой покупки взимается 11% НДС. Вопрос в том, сколько вы должны заплатить сверх чистой цены? Другими словами, что составляет 11% от 950 долларов?

поможет следующая формула:

Всего * Процент = Сумма

Предполагая, что общее значение находится в ячейке A2, а проценты в B2, приведенная выше формула превращается в простое = A2 * B2 и возвращает 104.50.

Помните, что когда вы набираете число, сопровождаемое знаком процента (%) в Excel, число интерпретируется как сотая часть его значения. Например, 11% фактически хранится как 0,11, и Excel использует это базовое значение во всех формулах и вычислениях.

Другими словами, формула = A2 * 11% эквивалентна = A2 * 0,11 . Естественно, вы можете использовать десятичное число, соответствующее проценту, непосредственно в формуле, если это лучше работает для ваших рабочих листов.

Пример 2. Расчет суммы по сумме и процентам

Например, ваш друг предложил вам свой старый компьютер за 400 долларов, что составляет 30% от первоначальной цены. Вы хотите знать, какова была первоначальная цена.

Поскольку скидка составляет 30%, сначала вы вычитаете ее из 100%, чтобы узнать, какой процент вы фактически должны заплатить (100% — 30% = 70%). Теперь вам нужна формула для расчета первоначальной цены, то есть, чтобы найти число, 70% которого равно 400.

Формула выглядит следующим образом:

Сумма / Процент = Всего

Применительно к реальным данным он может принимать любую из следующих форм:

= A2 / B2 или = A2 / 0.7 или = A2 / 70%

Как увеличить / уменьшить число в процентах

Приближается сезон отпусков, и это указывает на изменение ваших обычных еженедельных расходов. Вы можете рассмотреть различные варианты, чтобы узнать оптимальное еженедельное пособие.

Для увеличить сумму на процент, используйте эту формулу:

= Сумма * (1 +%)

Например, формула = A1 * (1 + 20%) увеличивает значение в ячейке A1 на 20%.

до уменьшите сумму на процент:

= Сумма * (1 -%)

Например, формула = A1 * (1-20%) уменьшает значение в ячейке A1 на 20%.

В нашем примере, если A2 — это ваши текущие расходы, а B2 — это процент, на который вы хотите увеличить или уменьшить эту сумму, вот формулы, которые вы бы ввели в ячейку C2:

Увеличение в процентах: = A2 * (1 + B2)

Уменьшить на процент: = A2 * (1-B2)

Как увеличить / уменьшить весь столбец на процент

Предположим, у вас есть столбец чисел, который вы хотите увеличить или уменьшить на определенный процент, и вы хотите иметь обновленные числа в том же столбце, а не добавлять новый столбец с формулой.

Вот 5 быстрых шагов для решения этой задачи:

Введите все числа, которые вы хотите увеличить или уменьшить, в некотором столбце, столбце B в этом примере.
В пустой ячейке введите одну из следующих формул:
Увеличение в процентах: = 1 + 20%
Уменьшить на процент: = 1-20%
Естественно, вы можете заменить 20% в вышеприведенных формулах на желаемый процент.
Выберите ячейку с формулой (в нашем случае C2) и скопируйте ее, нажав Ctrl + C.
Выберите диапазон ячеек, которые вы хотите изменить, щелкните правой кнопкой мыши выделенную область и выберите Специальная вставка…
В диалоговом окне Paste Special выберите Значения в Вставить , Умножьте в Операция и нажмите OK .

И вот результат — все числа в столбце B увеличены на 20%:

Таким же образом вы можете умножить или разделить столбец чисел на определенный процент.Просто введите желаемый процент в пустую ячейку и следуйте инструкциям выше.

Вот как вы рассчитываете процент в Excel. И даже если работа с процентами никогда не была вашим любимым видом математики, используя эти базовые формулы процента, вы можете заставить Excel выполнить эту работу за вас. На сегодня все, спасибо за чтение!

Вы также можете быть заинтересованы в:

Процентное изменение — процентное увеличение и уменьшение

Для объяснения и повседневных примеров использования процентов обычно смотрите нашу страницу Проценты: Введение . Для более общих процентных расчетов см. Нашу страницу Процентные калькуляторы .

Для расчета процентного увеличения:

Первое: вычислите разницу (увеличение) между двумя числами, которые вы сравниваете.

Увеличение = Новый номер — Оригинальный номер

Затем: разделите увеличение на исходное число и умножьте ответ на 100.

% увеличение = увеличение ÷ оригинальный номер × 100 .

Если ваш ответ отрицательный, то это процентное уменьшение.

Для расчета процентного уменьшения:

Первое: вычислите разницу (уменьшение) между двумя числами, которые вы сравниваете.

Уменьшение = Оригинальный номер — Новый номер

Затем: разделите уменьшение на исходное число и умножьте ответ на 100.

% Уменьшение = Уменьшение ÷ Оригинальный номер × 100

Если ваш ответ отрицательный, то это процентное увеличение.

Если вы хотите рассчитать процентное увеличение или уменьшение нескольких чисел, мы рекомендуем использовать первую формулу. Положительные значения указывают на процентное увеличение, тогда как отрицательные значения указывают на процентное уменьшение.

Калькулятор процентного изменения

Используйте этот калькулятор для расчета процентного изменения двух чисел

Подробнее: Процентные калькуляторы

Примеры — процентное увеличение и уменьшение

В январе Дилан работал в общей сложности 35 часов, в феврале он работал 45.5 часов — на сколько процентов увеличилось рабочее время Дилана в феврале?

Для решения этой проблемы сначала рассчитаем разницу в часах между новым и старым числами. 45,5 — 35 часов = 10,5 часов. Мы видим, что Дилан работал в феврале на 10,5 часов больше, чем в январе — это его увеличение на и на . Чтобы рассчитать увеличение в процентах, теперь необходимо разделить увеличение на исходное (январьское) число:

10,5 ÷ 35 = 0.3 (см. Нашу страницу , раздел для получения инструкций и примеров деления.)

Наконец, чтобы получить процент, мы умножаем ответ на 100. Это просто означает перемещение десятичного знака на два столбца вправо.

0,3 × 100 = 30

Дилан поэтому работал в феврале на 30% больше часов, чем в январе.

В марте Дилан снова работал 35 часов — так же, как в январе (или 100% его январских часов). Какая процентная разница между февральскими часами Дилана (45.5) а его мартовские часы (35)?

Сначала вычислите уменьшение в часах, то есть: 45,5 — 35 = 10,5

Затем разделите уменьшение на исходное число (февральские часы) так:

10,5 ÷ 45,5 = 0,23 (до двух десятичных знаков).

Наконец, умножьте 0,23 на 100, чтобы получить 23%. Часы Дилана в марте были на 23% ниже, чем в феврале.

Возможно, вы подумали, потому что между январскими часами Дилана (35) и февралем (45) произошло увеличение на 30%.5) часы, что также будет на 30% меньше между его февральскими и мартовскими часами. Как видите, это предположение неверно.

Причина в том, что наше исходное число отличается в каждом случае (35 в первом примере и 45,5 во втором). Это подчеркивает, насколько важно убедиться, что вы рассчитываете процент от правильной начальной точки.

Иногда проще показать процентное уменьшение как отрицательное число — для этого следуйте приведенной выше формуле для расчета процентного увеличения — ваш ответ будет отрицательным числом, если произошло уменьшение.В случае Дилана увеличение часов в период с февраля по март составляет -10,5 (отрицательный, потому что это уменьшение). Поэтому -10,5 ÷ 45,5 = -0,23. -0,23 × 100 = -23%.

Часы Дилана могут быть отображены в таблице данных как:

месяц	часов отработано	Процент Изменение
январь	35
февраля	45.5	30%
март	35	-23%

Расчет значений на основе процентного изменения

Иногда полезно иметь возможность рассчитывать фактические значения на основе процентного увеличения или уменьшения. Распространено видеть примеры того, когда это может быть полезно в СМИ.

Вы можете увидеть заголовки как:

В Великобритании количество осадков было этим летом на 23% выше среднего.
Показатели безработицы показывают снижение на 2%.
Банкиры ‘бонусы сократились на 45%.

Эти заголовки дают представление о тенденции — когда что-то увеличивается или уменьшается, но зачастую нет фактических данных.

Без данных цифры процентного изменения могут вводить в заблуждение.

В графстве Середигион в Западном Уэльсе очень низкий уровень насильственных преступлений.

Полицейские отчеты для Ceredigion в 2011 году показали 100% увеличение числа насильственных преступлений. Это поразительное число, особенно для тех, кто живет или думает о переезде в Ceredigion.

Однако, когда исходные данные изучаются, это показывает, что в 2010 году в Ceredigion было зарегистрировано одно насильственное преступление. Таким образом, увеличение на 100% в 2011 году означало, что было зарегистрировано два насильственных преступления.

Когда сталкиваются с фактическими цифрами, восприятие количества насильственных преступлений в Ceredigion значительно меняется.

Чтобы понять, насколько что-то увеличилось или уменьшилось в реальном выражении, нам нужны реальные данные.

Возьмите пример « осадков в Великобритании этим летом было на 23% выше среднего уровня » — мы можем сразу сказать, что в Великобритании выпало почти на четверть (25%) больше осадков, чем в среднем за лето.Тем не менее, не зная, каково среднее количество осадков или сколько осадков выпало за рассматриваемый период, мы не можем определить, сколько осадков выпало на самом деле.

Расчет фактического количества осадков за период, если известно среднее количество осадков.

Если мы знаем, что среднее количество осадков составляет 250 мм, мы можем рассчитать количество осадков за период путем расчета 250 + 23%.

Первая тренировка 1% из 250, 250 ÷ 100 = 2,5. Затем умножьте ответ на 23, потому что количество осадков увеличилось на 23%.

2,5 × 23 = 57,5.

Общее количество осадков за рассматриваемый период составило 250 + 57,5 = 307,5 мм.

Расчет среднего количества осадков, если фактическое количество известно.

Если в сообщении новостей говорится о новом измерении и процентном увеличении, « осадков в Великобритании были на 23% выше среднего … 320 мм осадков выпало… ».

В этом примере мы знаем, что общее количество осадков составило 320 мм. Мы также знаем, что это на 23% выше среднего. Другими словами, 320 мм соответствует 123% (или 1.23 раза) среднего количества осадков. Чтобы вычислить среднее значение, мы разделим сумму (320) на 1,23.

320 ÷ 1,23 = 260,1626. Округлено до одного знака после запятой, среднее количество осадков составляет 260,2 мм .

Теперь можно рассчитать разницу между средним и фактическим количеством осадков:
320 — 260,2 = 59,8 мм .

Мы можем сделать вывод, что 59,8 мм — это 23% от среднего количества осадков (260,2 мм), и что в реальном выражении выпало на 59,8 мм больше осадков, чем в среднем.

Мы надеемся, что вы нашли эту страницу полезной — почему бы не проверить наши другие страницы навыков счета? Или сообщите нам о предмете, который вы хотели бы видеть на SkillsYouNeed — Свяжитесь с нами .

Как рассчитать процент роста

Если вы хотите узнать, насколько ценность чего-либо возросла или уменьшилась с течением времени, вам часто нужно рассчитать процентное увеличение или уменьшение его стоимости. Например, в отчетах о фондовых рынках часто говорится, что определенная акция выросла или упала, скажем, на 5 процентов в течение дня. Для более конкретных вычислений вы можете оценить увеличение или уменьшение во времени с помощью более сложных формул.

Формула процентного увеличения

Если вы просто хотите увидеть процентное изменение значения с течением времени, есть общая и довольно простая формула, которую вы можете использовать.

Возьмите исходное значение и новое значение. Назовите их v1 и v2 для простоты. Затем вычтите v1 из v2, разделите результат на v1 и умножьте на 100, чтобы выразить значение в процентах. В математических терминах мы можем написать 100 * (v2 — v1) / v1.

Если значение положительное, это процентное увеличение, а если отрицательное, это процентное уменьшение. Естественно, если два значения равны, процентное изменение равно нулю.

Вы можете выполнить вычисления самостоятельно с помощью карманного калькулятора, приложения для калькулятора или ручки и бумаги, либо использовать специализированный онлайн-калькулятор, предназначенный для расчета процентных изменений.

A Конкретный пример

Например, представьте, что акция торгуется по 12 долл. На закрытии рынка в определенный день и торгуется по 10 долл., Когда рынок открылся. Мы хотим рассчитать процентное увеличение стоимости акций.

Итак, мы используем 100 * (12 — 10) / 10 = 100 * 2/10 = 200/10 = 20 процентов. Акции подорожали на 20 процентов в течение дневной торговой сессии.

Усреднение по временным интервалам

В некоторых случаях нам может потребоваться формула скорости роста, которая определяет, насколько значение в среднем изменилось за промежуточные интервалы времени.

Например, если стоимость этих акций выросла с 10 до 20 долларов за пять лет, мы могли бы узнать, насколько они увеличиваются в среднем каждый год.

Один из способов сделать это — просто разделить общее увеличение — в данном случае 100 процентов — на общее количество временных интервалов, чтобы мы получили 100/5 = 20 процентов в год. Это предполагает, что темпы роста были одинаковыми в течение каждого года, что может быть не так в других случаях.

В других случаях мы могли бы использовать более специализированную формулу для сбора других математических предположений, таких как экспоненциальный или логарифмический темп роста.Как правило, для разных отраслей и вариантов использования будут использоваться свои собственные конкретные формулы для различных сценариев, которые можно использовать непосредственно с помощью карманного калькулятора или электронной таблицы или с помощью специализированных цифровых инструментов.

APY и APR

Когда речь идет о процентных ставках, которые вы можете заработать на банковском счете, процентная ставка, по которой ваши деньги будут увеличиваться, обычно измеряется с использованием так называемой годовой процентной доходности, или APY. Это включает эффект начисления процентов, то есть выплату процентов по процентам, уже добавленным к эффективному балансу счета с течением времени.Скорость выражается в процентах, как следует из названия.

Когда речь идет о займах, которые вы берете, для обозначения суммы, которую вы платите за год, обычно используется цифра с аналогичным названием, называемая годовой процентной ставкой, или APR. APR не включает в себя эффекты накапливающегося интереса, в отличие от APY. Сюда входят и другие расходы, такие как расходы на закрытие ипотеки или сборы, взимаемые за перенос остатка по кредиту. Компании-эмитенты кредитных карт и другие организации, выдающие кредиты, как правило, обязаны указывать APR, а также ежемесячную ставку.

Формула для процента

Формула для процента является следующей, и она должна быть простой в использовании, если вы будете следовать простым указанным инструкциям. Внимательно изучите приведенную ниже формулу, прежде чем смотреть на примеры.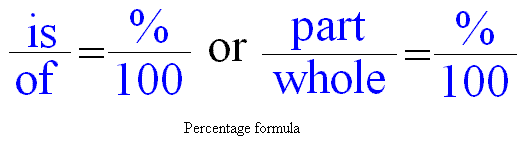

Мы возьмем несколько примеров для иллюстрации. Давайте начнем с формулы слева.

Важная вещь, которую нужно помнить, — это умножение после того, как вы определили различные части формулы.

Кросс-умножение означает умножение числителя одной дроби на знаменатель другой дроби.

Пример № 1:

25% из 200 — это ____

В этой задаче из = 200, — это =? И % = 25

Мы получаем:

— это /200 = 25/100

Поскольку — это неизвестное число , вы можете заменить его на y, чтобы сделать проблему более знакомой.

y / 200 = 25/100

Перемножить, чтобы получить y × 100 = 200 × 25

y × 100 = 5000

Разделить 5000 на 100, чтобы получить y

Поскольку 5000/100 = 50, y = 50

Итак, 25% из 200 — это 50

Пример № 2:

Какое число составляет 2% от 50?

Это просто еще один способ сказать, что 2% из 50 — это ___

Итак, установите пропорцию, как в примере № 1:

— это /50 = 2/100

Замените на y и умножьте на умножение, чтобы получить :

y × 100 = 50 × 2

y × 100 = 100

Поскольку 1 × 100 = 100, y = 1

Следовательно, 1 составляет 2% от 50

Пример № 3:

24 % от ___ составляет 36

На этот раз обратите внимание, что это = 36, но из отсутствует

После настройки формулы вы получите:

36/ из = 24/100

Заменить от y и умножить на кросс, чтобы получить:

36 / y = 24/100

y × 24 = 36 × 100

y × 24 = 3600

Разделить 3600 на 24, чтобы получить y

3600/24 = 150 , y = 150

Следовательно, 24% из 150 — это 36

Как использовать другую формулу для процента справа.

Теперь мы возьмем примеры, чтобы проиллюстрировать, как использовать формулу для процентного соотношения справа

Пример № 4:

Чтобы использовать другую формулу, которая говорит, что часть и целое, просто запомните следующее:

Число после из всегда целое.

Число после равно , всегда является частью.

Если проблема говорит, что 25% от ___ равно 60, то мы знаем, что целое отсутствует, а часть = 60

Ваша пропорция будет такой:

60/ целое = 25/100

После кросс-умножения мы получить:

целых × 25 = 60 × 100

целых × 25 = 6000

Разделить 6000 на 25, чтобы получить целых

6000/25 = 240, поэтому целых = 240

Следовательно, 25% от 240 равно 60

Пример № 5:

___% от 45 равно 9

Здесь целое = 45 и частично = 9, но % отсутствует

Мы получаем:

9/45 = % / 100

Замена% на x и перекрестное умножение дает:

9 × 100 = 45 × x

900 = 45 × x

Разделите 900 на 45, чтобы получить x

900/45 = 20, поэтому x = 20

Вот и мы! Я надеюсь, что формула для процента была полезна.

Новые уроки математики

Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.