Онлайн калькулятор: Гидростатическое давление
Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:
Калькулятор позволяет найти
- давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
- высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
- плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
- ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости
Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения — земное ускорение, и для давления — величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.

Гидростатическое давление
Найтидавлениеплотностьвысотаускорение свободного паденияТочность вычисленияЗнаков после запятой: 2
Давление в жидкости, Па
Высота столба жидкости, м
Плотность жидкости, кг/м3
Ускорение свободного падения, м/с2
save Сохранить share Поделиться extension Виджет
Гидростатическое давление — давление столба воды над условным уровнем.
Формула гидростатического давления выводится достаточно просто
Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
Также это приводит к такому явлению как гидростатический парадокс.
Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.
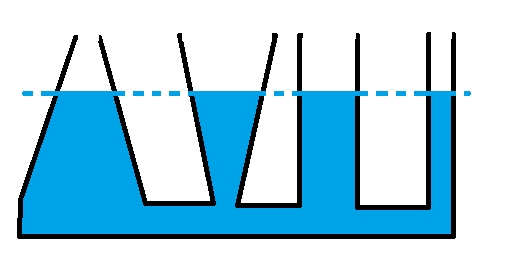
На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда
Источники в википедии: Гидростатическое давление Гидростатический парадокс
Гидростатическое давление — Википедия
Гидростатическое давление — давление столба жидкости над условным уровнем.
Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение
Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах[1].
В каждой жидкости существует давление, обусловленное её собственным весом p=G/S=mg/S{\displaystyle p=G/S=mg/S}; так как m=ρV{\displaystyle m=\rho V}, то p=ρgV/S{\displaystyle p=\rho gV/S}; учтём, что V=Sh{\displaystyle V=Sh} и получим формулу p=ρgh{\displaystyle p=\rho gh}.
Плотность жидкости ρ{\displaystyle \rho } зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением[2].
Для бытовых расчетов можно принять, что с ростом глубины на каждые 10 метров пресной воды, давление увеличивается на 0,1 МПа (1 атмосфера).
Это основное свойство жидкостей было открыто и проверено на опыте Блезом Паскалем в 1653 г., хотя несколько ранее оно было уже известно Стевину
Единицей измерения давления в международной системе единиц является Паскаль. На практике гидростатическое давление часто измеряют в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0 °C при нормальном ускорении свободного падения 9,80665 м/с².
На основании гидростатического парадокса можно гидростатическое давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности.
- Гидростатическое давление в любой точке одинаково по всем направлениям.
- Гидростатическое давление жидкости на глубине h{\displaystyle h} c силой давления на свободную поверхность p0{\displaystyle p_{0}} равно p=p0+ρgh{\displaystyle p=p_{0}+\rho gh} (основное уравнение гидростатики)
 Гидростатическое давление на тело не зависит от направления.
Гидростатическое давление на тело не зависит от направления.Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние каждой такой частицы от свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу гидростатического давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.
Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, гидростатическое давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.
Закон Паскаля[править | править код]
Чем глубже, тем выше давление.Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести (= несжимаемая жидкость) подчиняется закону Паскаля:
- p(h)=ρgh{\displaystyle p(h)=\rho \,g\,h}
где:
- ρ{\displaystyle \rho } — плотность [для пресной воды: ρ ≈ 1000 кг/м³]
- g{\displaystyle g} — ускорение свободного падения [для Европы: g ≈ 9,81 м/с²]
- h{\displaystyle h} — высота (здесь: жидкости) [м]
- p{\displaystyle p} — [Па]
⇒ p(h){\displaystyle p(h)} = гидростатическое давление (p) зависит от высоты (h) жидкости.[4]
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Давление и Вакуум / / Таблица — давление водяного столба в зависимости от глубины (высоты водяного столба) 1-500 метров Па=Pa, бар=bar, psi, psf. Гидростатическое давление столба жидкости или газа. Таблица давления воды от глубины. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расчет давления жидкости на дно и стенки сосуда. Видеоурок. Физика 7 Класс
В ходе этого урока с помощью математических преобразований и логических умозаключений будет получена формула для расчета давления жидкости на дно и стенки сосуда.
Тема: Давление твердых тел, жидкостей и газов
Урок: Расчет давления жидкости на дно и стенки сосуда
Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 1).
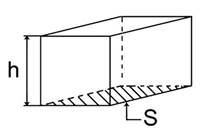
Рис. 1. Сосуд для расчета давления жидкости
Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу, действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде
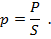
Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m
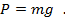
Напомним, что символом g обозначено ускорение свободного падения.
Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V
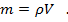
Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда
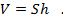
Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:
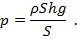
В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:
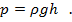
Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.
Полученная выше формула называется формулой гидростатического давления. Она позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.
Рассмотрим несколько примеров.
Возьмем два сосуда. В одном из них находится вода, а в другом – подсолнечное масло. Уровень жидкости в обоих сосудах одинаков. Одинаковым ли будет давление этих жидкостей на дно сосудов? Безусловно, нет. В формулу для расчета гидростатического давления входит плотность жидкости. Поскольку плотность подсолнечного масла меньше, чем плотность воды, а высота столба жидкостей одинакова, то масло будет оказывать на дно меньшее давление, чем вода (Рис. 2).

Рис. 2. Жидкости с различной плотностью при одной высоте столба оказывают на дно различные давления
Еще один пример. Имеются три различных по форме сосуда. В них до одного уровня налита одна и та же жидкость. Будет ли одинаковым давление на дно сосудов? Ведь масса, а значит, и вес жидкостей в сосудах различен. Да, давление будет одинаковым (Рис. 3). Ведь в формуле гидростатического давления нет никакого упоминания о форме сосуда, площади его дна и весе налитой в него жидкости. Давление определяется исключительно плотностью жидкости и высотой ее столба.

Рис. 3. Давление жидкости не зависит от формы сосуда
Мы получили формулу для нахождения давления жидкости на дно и стенки сосуда. Этой формулой можно пользоваться и для расчета давления в объеме жидкости на заданной глубине. Она может быть использована для определения глубины погружения аквалангиста, при расчете конструкции батискафов, подводных лодок, для решения множества других научных и инженерных задач.
Список литературы
- Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
- Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Единая коллекция цифровых образовательных ресурсов (Источник).
- Единая коллекция цифровых образовательных ресурсов (Источник).
Домашнее задание
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов №504–513.
Калькулятор расчета давления воды в водопроводе + подробное описание опыта
Нередко случается так, что давление воды на точках водоразбора в квартире – явно недостаточное. Это приводит к неудобствам при пользовании сантехническими приборами, к «зависанию» или полной остановке бытовой техники, подключенной к водопроводу, к некорректной работе современных устройств (душевых кабинок, джакузи, биде и т.п.), требующих определенного напора воды. Естественно, такая ситуация требует принятия мер административного характера (которые помогают, увы, не всегда), или установки специальных повышающих насосов или насосных станций.
Калькулятор расчета давления воды в водопроводеЧтобы предъявить претензии или спланировать установку дополнительного оборудования, желательно заранее знать, какое же давление преимущественно держится в водопроводе, то есть насколько оно отличается от нормативного. Если есть манометр, то снять показания — труда не составит. Но что делать, если такого прибора нет? Не беда, существует простой и точный экспериментальный способ, под который и составлен расположенный ниже калькулятор расчета давления воды в водопроводе.
Цены на насосные станции
насосная станция
Описание проведения замеров и расчетов – в текстовой части ниже калькулятора.
Калькулятор расчета давления воды в водопроводе
Перейти к расчётам
Как провести опытные замеры и вычисления?
Для самостоятельного измерения давления потребуется отрезок прозрачного шланга (трубки) длиной порядка 2 метров. Диаметр в данном случае никакого решающего значения не имеет – главное, чтобы была возможность герметично надеть шланг на смеситель или любой другой патрубок, оснащенный запорным краном.
Далее, поступают следующим образом (см схему):
Схема проведения экспериментального вычисления давления в водопроводе.- Шланг надевается на смеситель или патрубок, герметично, чтобы не просачивались ни вода, ни воздух. Лучше всего – обтянуть обычным хомутом.
- В шланг запускается небольшое количество воды, затем он понимается вертикально и фиксируется в таком положении. Уровень воды в нижней петле должен приходиться примерно на высоту крана (патрубка). Это наглядно показано на иллюстрации слева. После этого замеряют начальную длину воздушного столба ho в миллиметрах. Значение записывают.
- Далее, шланг сверху герметично закупоривают какой-нибудь пробкой, а затем открывают кран полностью. Вода своим давлением сожмет воздух в трубке и поднимется на определенную высоту. Главное – ни в коем случае не допустить просачивания воздуха сверху.
- После того как уровень стабилизируется, делают еще один промер высоты воздушного столба (на рисунке справа) – hэ.
Эти две величины и являются исходными для внесения в калькулятор и получения значения давления воды в водопроводе. Результат будет выдан в технических атмосферах (бар) и в метрах водяного столба – как кому удобнее.
Одно из решений проблемы – установка насосной станции
Ситуацию со стабильно недостаточным напором воды можно решить установкой насосной станции с аккумулирующим резервуаром. Как правильно подойти к выбору насосной станции – читайте в специальной публикации нашего портала.
Формула давления
ОПРЕДЕЛЕНИЕДавление столба жидкости (гидростатическое давление) равно плотности этой жидкости, умноженной на высоту столба жидкости и ускорение свободного падения.
Здесь – давление, – плотность жидкости, – ускорение свободного падения ( м/с), – высота столба жидкости (глубина, на которой находится сдавливаемое тело).
Единица измерения давления – Па (паскаль).
Это векторная величина. В каждой точке жидкости давление одинаково во всех направлениях. Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:
Где – сила тяжести, действующая на жидкость (её вес), – площадь поверхности, на которую оказывается давление.
Примеры решения задач по теме «Давление»
ПРИМЕР 1| Задание | Высота воды в аквариуме 1 м. Найти давление на дно аквариума. |
| Решение | Напоминаем, плотность воды кг/м, а м/с. Таким образом:
(Па) |
| Ответ | Давление воды составляет 9800 Паскаль. |
| Задание | Закрытый сосуд устроен так, что его крышка подвижна (см. рисунок). Сосуд наполнен жидкостью, плотность которой известна. На крышку сосуда действует сила . Найти давление на дно сосуда, если известны площадь дна и крышки и объём жидкости в сосуде. |
| Решение | Пусть:
– площадь крышки – площадь дна – объём жидкости – плотность жидкости Крышка подвижна, значит она давит на жидкость с той силой, с которой внешние силы давят на неё сверху. Очевидно: Попробуем найти давление жидкости: Соберём всё вместе: |
| Ответ |
Все формулы по физике
Формула силы выталкивания
Формула напряжённости магнитного поля
Формула силы Ампера
Формула силы Лоренца
Формула ЭДС
Формула длины волны
Давление. Давление столба жидкости. Закон Паскаля. Гидростатика | LAMPA
Гидростатика. Закон Паскаля
Раздел гидростатики в физике занимается давлениями неподвижных жидкостей. Нечто похожее у нас уже было в разделе «Статика», когда мы рассматривали неподвижность твёрдых тел, рассматривали правило моментов: чтобы вращающие моменты уравновешивали друг друга.
В гидростатике – нечто похожее: рассматриваются давления жидкости в условии, когда она неподвижна – то есть не течёт. Для этого раздела важен закон Паскаля:
Давление жидкости передаётся в любую точку без изменения во всех направлениях.
Сложная формулировка. Сложный закон. Понять его можно на примере. Возьмём полиэтиленовый пакет, нальём в него жидкость и сделаем несколько небольших дырочек. Будем давить сверху на этот пакет с жидкостью. Что мы увидим? Вода будет литься из каждой дырочки.

И можно заметить, что наше давление сверху на пакет будет передаваться без изменения в каждую «дырочку» пакета – струйки воды получатся примерно одинаковые, хоть и будут направлены в разные стороны.
Получается, что если до некоторой точки жидкости дошло давление, то давление от этой точки будет распространяться во все стороны.

На основе закона Паскаля основано действие различных гидравлических прессов и других механических устройств, в которых требуется передача давления чего-либо из одной точки – в другую точку (например – экскаватора, тормозной системы автомобилей). Такое устройство может представлять собой трубку, внутри которой находится жидкость. С одной стороны трубки – давят на жидкость, жидкость передаёт это давление – и давит на что-то с другого конца трубки.

Для того чтобы закон Паскаля стал вам окончательно понятен, приведём ещё один пример. Допустим, у нас есть палка. Просто палка. И мы давим этой палкой на землю. Действуем сверху вниз. Если земля не слишком твёрдая, то палка «уйдёт» у нас вниз. И только вниз. Ни вбок, ни вверх. Вниз.

Рассмотрим другой случай. Пусть у нас есть трубка, а на её конце – резиновый шарик. А внутри трубки и шарика – жидкость. Тогда, если мы будем давить на жидкость в трубке, то шарик у нас будет раздуваться во все стороны. Не только вниз, не только вбок – а во все стороны сразу. То есть давление в жидкости передаётся во все стороны, а давление в твёрдых телах – преимущественно в том направлении, в котором приложено давление.
