Расчёт сложных процентов в Excel
Уроки MS Excel
Работая с таблицами Excel, иногда возникает необходимость в распределении информации из одного столбца по
Уроки MS Excel
Тем людям, которые регулярно работают с таблицами Excel, нужно часто выполнять одни и те
Уроки MS Excel
Нередко пользователям приходится перенести часть информации с документа Microsoft Word в Excel формат, чтобы
Уроки MS Excel
Огромное преимущество электронных таблиц Excel заключается в том, что пользователю доступна работа как с
Уроки MS Excel
Пользователю Excel нередко приходится сталкиваться с тем, чтобы определять, сколько строк содержит таблица. Чтобы
Excel – одна из лучших программ для аналитика данных. А почти каждому человеку на
А почти каждому человеку на
Уроки MS Excel
Время от времени при работе с электронными таблицами появляется необходимость изменить положение нескольких рядов
Уроки MS Excel
Excel – удивительная программа, дающая возможность не только числовые данные обрабатывать. С ее помощью
Уроки MS Excel
Сейчас век информации. Количество данных, которые людям приходится обрабатывать каждый день, растет все больше
Уроки MS Excel
Определение процента от числа – довольно частая задача, с которой приходится сталкиваться пользователю Ecxel,
Уроки MS Excel
Excel – невероятно функциональная программа. Она может использоваться и в качестве некого подобия среды
Уроки MS Excel
Excel – невероятно функциональная программа, позволяющая не просто записывать данные в табличном виде, но
Уроки MS Excel
Стандартное обозначение строк в Excel – цифровое.
Уроки MS Excel
Набор функций у программы Excel, конечно, поистине огромный. В том числе, можно в определенной
Уроки MS Excel
При работе с Excel могут возникать различные ситуации, такие как сбои в поставках электроэнергии,
Важно понимать, что Excel – это не только программа для создания баз данных, но
Калькулятор онлайн — Калькулятор процентов. Сложные проценты. Депозитный калькулятор
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Понятие о проценте
Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.
Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается
процент знаком %, Таким образом,
1% — это 0,01, или \( \frac{1}{100} \) часть величины
Приведем примеры:
— 1% от минимальной заработной платы 2300 р.
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).
Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.
Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.
Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.
Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.
Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:
\( 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 \)Для обратного перехода выполняется обратное действие.
\( 0,58 = (0,58 \cdot 100)\% = 58\% \) \( 0,045 = (0,045 \cdot 100)\% = 4,5\% \)
В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.
Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.
Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.
Задачи на проценты
Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.
В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.
1. Нахождение процента от числа.
Чтобы найти \( \frac{p}{100} \) от a, надо a умножить на \( \frac{p}{100} \):
Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x
2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac{p}{100} , \; (p \neq 0) \), надо b разделить на \( \frac{p}{100} \):
\( a = b : \frac{p}{100} \)
3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а
затем эту часть выразить в процентах:
Например, 9 г соли в растворе массой 180 г составляют \( \frac{9 \cdot 100}{180} = 5\% \) раствора.
Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.
Нетрудно заметить, что формулы
\( b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.Составные задачи на проценты решаются аналогично задачам на дроби.
Простой процентный рост
Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа
— наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма
составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р.,
а всего 1019 р.
Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма
составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р.,
а всего 1019 р.
Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.
Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму,
которую должен заплатить человек после n дней просрочки, обозначим Sn.
Тогда за n дней просрочки пеня составит рn% от S, или \( \frac{pn}{100}S \), а всего придется заплатить
\( S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S \)
Таким образом:
\( S_n = \left( 1+ \frac{pn}{100} \right) S \)
Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.
Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов.
Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac{pn}{100} \right) S \)
Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».
Сложный процентный рост
В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный
договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете
доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход -
«проценты», как его обычно называют.
Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.
Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.
10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)
10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)
10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)
Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.
А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,12 раз.
Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,12 = 1,13 раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,13 • 1000 = 1,331 • 1000 — 1331 (р.)
Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма,
которая будет на счете через n лет, равна Sn р. n S \)
n S \)
Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.
Как рассчитать сложные проценты в Excel?
Как рассчитать сложные проценты в Excel?
Если у вас есть банковский счет, по которому могут начисляться проценты каждый год и десять лет спустя, сколько всего процентов вы можете получить со своего счета? В этом случае я говорю о том, как рассчитать сложный процент в Excel.
Сложные проценты возникают, когда проценты добавляются к основной сумме депозита или ссуды, так что с этого момента добавленные проценты также приносят проценты.
Расчет сложных процентов по формуле в Excel
Расчет сложных процентов по функциям в Excel
Вкладка Office позволяет редактировать и просматривать в Office с вкладками и значительно упрощает работу …
Kutools for Excel решает большинство ваших проблем и увеличивает вашу производительность на 80%
- Повторное использование чего угодно: Добавляйте наиболее часто используемые или сложные формулы, диаграммы и все остальное в избранное и быстро используйте их в будущем.
- Более 20 текстовых функций: Извлечь число из текстовой строки; Извлечь или удалить часть текстов; Преобразование чисел и валют в английские слова.
- Инструменты слияния: Несколько книг и листов в одну; Объединить несколько ячеек / строк / столбцов без потери данных; Объедините повторяющиеся строки и сумму.
- Разделить инструменты: Разделение данных на несколько листов в зависимости от ценности; Из одной книги в несколько файлов Excel, PDF или CSV; От одного столбца к нескольким столбцам.
- Вставить пропуск Скрытые / отфильтрованные строки; Подсчет и сумма по цвету фона; Отправляйте персонализированные электронные письма нескольким получателям массово.
- Суперфильтр: Создавайте расширенные схемы фильтров и применяйте их к любым листам; Сортировать по неделям, дням, периодичности и др .
 12=0.88638487 раз). Иными словами, реальная (сложная, эффективная) процентная ставка составляет примерно 12,7% при начислении (при удержании — примерно 11,4%). И т. д. Впрочем, если речь о кредите, реальный процент надо считать не «удерживаемым», а «начисляемым», поскольку он первым делом НАЧИСЛЯЕТСЯ на сумму долга (ПРИБАВЛЯЕТСЯ к ней), а не вычитается из чего-то там еще. То есть, если вы одолжили деньги под 1% в месяц, то годовая цена кредита — около 12,7% в год, а не 12% и уж тем паче не 11,4%.
12=0.88638487 раз). Иными словами, реальная (сложная, эффективная) процентная ставка составляет примерно 12,7% при начислении (при удержании — примерно 11,4%). И т. д. Впрочем, если речь о кредите, реальный процент надо считать не «удерживаемым», а «начисляемым», поскольку он первым делом НАЧИСЛЯЕТСЯ на сумму долга (ПРИБАВЛЯЕТСЯ к ней), а не вычитается из чего-то там еще. То есть, если вы одолжили деньги под 1% в месяц, то годовая цена кредита — около 12,7% в год, а не 12% и уж тем паче не 11,4%.Проценты (за долг, например, или на банковский депозит) могут сочетаться с регулярным или нерегулярным поступлением/съемом денег. В таком случае надо посчитать увеличение (суммы долга или депозита) к моменту поступления/съема (считаете во сколько раз и умножаете результат на исходную сумму) и затем добавить или вычесть (знак — по обстоятельствам: увеличивается сумма долга/депозита или снижается) поступление/съем, а дальнейшие проценты пойдут уже на эту сумму или разность. Если таких операций много, можно все считать в электронной таблице, написав один раз формулу с неизвестными из разных столбцов. Если поступление/съем периодичны и в постоянных суммах, можно применить формулу для суммы геометрической прогрессии (прогрессия там появляется очевидным образом), но это, вероятно не для вас, раз у вас проблемы даже с «формулой процентов». Дай бог, чтобы хоть с электронной таблицей у вас получилось.
ЧТО ТАКОЕ СЛОЖНЫЙ ПРОЦЕНТ? ФОРМУЛА, ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ — НАУКИ
Сложные проценты — это проценты, выплачиваемые на первоначальную основную сумму.и от накопленных прошлых процентов. Когда вы занимаете деньги в банке, вы платите проценты. На самом деле проценты — эт
Содержание:
Сложные проценты — это проценты, выплачиваемые на первоначальную основную сумму.и от накопленных прошлых процентов.
Когда вы занимаете деньги в банке, вы платите проценты.
 На самом деле проценты — это плата за заем денег, обычно это процент, взимаемый с основной суммы в течение года.
На самом деле проценты — это плата за заем денег, обычно это процент, взимаемый с основной суммы в течение года.Если вы хотите знать, сколько процентов вы получите от своих инвестиций, или если вы хотите знать, сколько вы заплатите сверх стоимости основной суммы по ссуде или ипотеке, вам необходимо понять, как работают сложные проценты.
Пример сложного процента
Подумайте об этом так: если вы начнете со 100 долларов и получите 10 долларов в качестве процентов в конце первого периода, у вас будет 110 долларов, по которым вы можете заработать проценты во втором периоде. Таким образом, во втором периоде вы получите проценты в размере 11 долларов. Теперь на 3-й период у вас есть 110 + 11 = 121 доллар, на который вы можете заработать проценты. Таким образом, в конце 3-го периода вы заработаете проценты на 121 доллар. Сумма будет 12.10. Теперь у вас 121 + 12,10 = 132,10, из которых вы можете получать проценты. Следующая формула вычисляет это за один шаг, а не делает расчет для каждого периода начисления процентов по одному шагу за раз.
Формула сложных процентов
Сложные проценты рассчитываются на основе основной суммы долга, процентной ставки (годовой или годовой процентной ставки) и времени:
п это основная сумма (начальная сумма, которую вы занимаете или вносите)
р годовая процентная ставка (в процентах)
п — количество лет, на которые сумма депонируется или заимствуется.
А сумма денег, накопленная через n лет, включая проценты.
При начислении процентов один раз в год:
А = Р (1 + г)п
Однако, если вы одалживаете на 5 лет, формула будет выглядеть так:
А = Р (1 + г)5
Эта формула применима как к вложенным, так и к заемным деньгам.
Частое начисление процентов
Что, если проценты выплачиваются чаще? Это не намного сложнее, если не считать изменения скорости.
 Вот несколько примеров формулы:
Вот несколько примеров формулы:Ежегодно =п × (1 + r) = (годовое начисление)
Ежеквартально =п (1 + r / 4) 4 = (квартальное сложение)
Ежемесячно =п (1 + r / 12) 12 = (ежемесячное начисление сложных процентов)
Таблица сложных процентов
Смущенный? Может быть полезно изучить график работы сложных процентов. Скажем, вы начинаете с 1000 долларов и 10% процентной ставки. Если бы вы платили простые проценты, вы бы заплатили 1000 долларов США + 10%, что составляет еще 100 долларов, на общую сумму 1100 долларов, если вы заплатили в конце первого года. По истечении 5 лет общая сумма простых процентов составит 1500 долларов.
Сумма, которую вы платите в виде сложных процентов, зависит от того, как быстро вы погасите ссуду. Это всего лишь 1100 долларов в конце первого года, но через 5 лет вырастет до 1600 долларов. Если продлить срок кредита, сумма может быстро вырасти:
Год Первоначальный заем Интерес Кредит в конце 0 $1000.00 $1,000.00 × 10% = $100.00 $1,100.00 1 $1100.00 $1,100.00 × 10% = $110.00 $1,210.00 2 $1210.00 $1,210.00 × 10% = $121.00 $1,331.00 3 $1331.00 $1,331.00 × 10% = $133.10 $1,464.10 4 $1464.10 $1,464.10 × 10% = $146.41 $1,610.51 5 $1610.51 Под редакцией Энн Мари Хелменстайн, доктора философии.
Format mla apa chicago Your Citation Russell, Deb. «Что такое сложный процент? Формула, определение и примеры». ThoughtCo, 26 августа 2020 г., thinkco.com/what-is-compound-interest-3863068. Рассел, Деб. (2020, 26 августа). Что такое сложный процент? Формула, определение и примеры. Получено с https://www.oughttco.com/what-is-compound-interest-3863068 Russell, Deb. «Что такое сложный процент? Формула, определение и примеры». ThoughtCo. https://www.oughttco.com/what-is-compound-interest-3863068 (по состоянию на 15 февраля 2021 г.).
Рассел, Деб. (2020, 26 августа). Что такое сложный процент? Формула, определение и примеры. Получено с https://www.oughttco.com/what-is-compound-interest-3863068 Russell, Deb. «Что такое сложный процент? Формула, определение и примеры». ThoughtCo. https://www.oughttco.com/what-is-compound-interest-3863068 (по состоянию на 15 февраля 2021 г.).Смотреть сейчас: Как рассчитать сложный процент
Расчёт, формулы сложных процентов в Excel + калькулятор
Приветствую, читатели и посетители блога!
«Превратите 1$ в 1000000$!», «Самый простой способ стать миллионером!», «Вложи, ничего не делай и стань финансово свободным!». Вам попадались такие лозунги в Интернете? Мне да…
Впрочем, такие фразы возникли не на пустом месте. Любая статья, обучающий курс или другие материалы с таким заголовком – так или иначе, затрагивает тему сложного процента.
Вот и я вам предлагаю сегодня поговорить об этом удивительном инструменте богатства. Еще в самом начале ведения блога я затрагивал эту тему, когда искал ответ на вопрос – Зачем нужны инвестиции?.
Для начала, давайте разберемся кое в чём. Если есть сложный процент, есть и простой, не так ли? В чем разница?
И то, и другое — это способ начисления прибыли на депозиты и вложения. Но формулы сложных и простых процентов отличаются кардинально: в первом случае работает арифметическая прогрессия, во втором – геометрическая.
Если по-русски, то ключевое отличие двух процентов в том, что при простом проценте доход приносит только первоначальная сумма. Прибыль всегда будет одинаковой и через год, и через 10 лет.
Например, если инвестор получает 20% в год на 10000$ — это 2000$ в год. И каждый год сумма прибыли будет ровно 2000$.
С другой стороны, когда работает сложный процент, процент прибыли начисляется не только на первичную сумму инвестиций, но еще и на полученную прибыль. Это значит, что с каждым годом доход будет все выше и выше.

На тех же условиях, но с реинвестированием – в первый год инвестор получит 2000$, во второй – 2400$, в третий – 2880$. А через десять лет – 10320$! А через двадцать – невероятные 63896$. Что мы там говорили о том, как стать миллионером?
И это без учета дополнительных вложений.
Очень похоже на то, как катится с горы снежный ком – сначала понемногу, а со временем ком становится все больше и больше – и вот уже он огромен!
Для наглядности я сделал другой расчет сложных процентов в Excel и сравнил с простыми:
С каждым годом, с каждым месяцем разница все ощутимее и ощутимее
И чем дальше, тем сильнее заворачивается вверх красный график, устремляясь по параболе в финансовую бесконечность… Пусть и в теории, но зато как эффектно!
В принципе, особо тут разглагольствовать не о чем. В Интернет-инвестировании эффект сложного процента разрешен и чаще всего используется автоматически. Например, в ПАММ-счетах это так.
С другой стороны, инвесторам часто приходится рассчитывать сложный процент – подсчитать доходность, оценить инвестиционный горизонт… И решать другие прикладные задачи.
Поэтому дальше я покажу вам все необходимые формулы и помогу с расчетами.
Содержание:
Обзор задач и формул сложных процентов
Самая первая задача, с которой может столкнуться инвестор – «Сколько я получу денег, инвестируя»? Она решается, если известна начальная сумма и годовая процентная ставка доходности.
Для расчета используется формула сложных процентов с капитализацией:
Где:
- К0 — начальный капитал,
- К – результат инвестирования (финальный капитал)
- R – годовая процентная ставка
- m – период реинвестирования (в месяцах)
- n – количество периодов реинвестирования (месяцев, кварталов, лет)
Чтобы работать чисто с годовыми периодами, нужно убрать из знаменателя 12, а из числителя – m.
 Но я этого делать не буду, так как ПАММ-счета удобнее всего анализировать через среднемесячную доходность.
Но я этого делать не буду, так как ПАММ-счета удобнее всего анализировать через среднемесячную доходность.Давайте рассмотрим пару примеров.
Пример №1. Иван Иванов положил 7000$ на депозит в банке. Сейчас средняя ставка по долларовым депозитам в Украине – в районе 9% в год. Вклад будет переоформляться каждый год в течение 10 лет. Сколько в итоге будет денег на банковском счету?
К0 =7000$, R = 9% в год, m = 12 месяцев, n = 10 (10 периодов по 12 месяцев)
Капитал вырос почти в три раза, несмотря на мизерную доходность по депозитам.
Впрочем, деньги на ПАММ-счетах реинвестируются автоматически и постоянно. Кроме того, гарантий стабильного годового дохода нет…
Поэтому рекомендую для расчетов сложного процента в ПАММ-счетах использовать ежемесячный реинвест.
Пример №2. Пётр Петров вложил в ПАММ-счета 10000$. После анализа статистики выяснилось, что он может ожидать 30% чистой прибыли за год. И теперь Пётр хочет знать, каким будет размер капитала через полгода.
Вот, что получилось:
К0 =10000$, R = 30% в год, m = 1 месяц, n = 6 (6 периодов по 1 месяцу)
Для сравнения, без реинвестирования инвестор получил бы 11500$. То есть, на 97$ меньше, что почти не чувствуется – это всего лишь 0.97% от общего капитала.
Но давайте теперь посмотрим чуть дальше в следующем примере.
Пример №3. Исидор Сидоров вложил в ПАММ-счета 5000$. Он собирается активно управлять портфелем и рассчитывает на 50% в год в течение 5 лет. Какой капитал получится в итоге?
Для расчета снова используется формула сложных процентов. Только теперь периодов не 6, а 60 – в 5 годах 60 месяцев. Сколько же получилось?
К0 =5000$, R = 50% в год, m = 1 месяц, n = 60 (60 периодов по 1 месяцу)
Без реинвестирования прибыль составила бы 50%*5=250%.
 Соответственно, капитал бы вырос до 35000$. А с учетом сложного процента – на целых 106 тысяч! Теперь разница ощущается очень сильно.
Соответственно, капитал бы вырос до 35000$. А с учетом сложного процента – на целых 106 тысяч! Теперь разница ощущается очень сильно.И чем больше проходит времени, тем сильнее разница. Теоретически, вложив сегодня 1$ в банк, уже ваши правнуки стали бы миллионерами.
Я не раз видел, как эту «фишку» используют в фильмах. Например, сюжет может быть такой:
Когда-то давно кто-то спрятал честно или нечестно заработанные деньги в скромный банк. И забыл о деньгах. Или надолго попал в тюрьму. Или умер. В общем, о деньгах забыли.
И вот, через 20-30 лет этот счет обнаруживают, а там лежат миллионы или даже миллиарды долларов. И начинается охота за паролями, поиск владельца, взлом хитромудрых защитных систем и т.д. Что придумают сценаристы 🙂
В прошлой статье я упоминал о том, что консервативные ПАММ-счета растут по параболе из-за сложного процента. Теперь вы на 100% понимаете, как это работает!
Кроме постоянного реинвестирования прибыли, инвестор может дополнительно «доливать» деньги в свой портфель. Эти деньги тоже будут приносить доход, поэтому формула сложных процентов немного усложняется.
Ну как немного… В общем, смотрите:
AI (Additional Investments) – размер постоянного пополнения.
С левым слагаемым вы знакомы, а правое – расчет сложного процента по новым вложениям. Формула правильная, я проверял 🙂
———— ↑ к содержанию ↑ ————
Вспомогательные формул расчета сложных процентовИз формулы, которую мы использовали раньше, можно получить несколько других, которые могут пригодиться инвестору при решении финансовых задач.
Например, иногда нужно найти не финальный, а начальный капитал.
Пример №4. Аркадий Аркадьев интересуется, сколько ему нужно вложить денег, чтобы получить через 5 лет при ставке доходности 30% в год 100000$.
 Реинвест – каждый квартал.
Реинвест – каждый квартал.Для этого мы используем такую формулу:
Выглядит немного страшно, но цифры точно те же, что мы использовали до этого. Подставим наши данные в формулу и найдем начальный капитал:
K = 100000$, R = 30% в год, m = 3 месяца, n = 20 (5 лет – это 20 кварталов)
Оказалось, нужно почти в 5 раз меньше. Круто, не так ли?
Идем дальше. Давайте представим ситуацию – инвестор хочет вложить деньги на определенный срок. И он рассчитывает по итогам достичь определенной суммы капитала. Какую процентную ставку ему нужно получить?
Чтобы это узнать, для расчета нам нужна формула сложных процентов для средней процентной ставки:
Пример №5. Начальные инвестиции Максима Максимова – 13000$. Через два года они должны превратиться в 18000$. Реинвест ежемесячный (m= 1). Под какую ставку доходности Максиму нужно собирать инвестиционный портфель, чтобы выйти на требуемую сумму?
Подставляем числа:
K = 18000$, К0 =13000$, m = 1 месяц, n = 24 (2 года = 24 месяца)
Естественно, это годовая ставка. Её можно превратить в месячную, если из числителя убрать 12, и тогда получится около 1.5% в месяц – минимальный порог для ПАММ-счетов.
Что там можно еще найти? Ах, да – сколько нужно времени, чтобы получить определенную сумму при определенной ставке. Давайте попробуем 🙂
Если в прошлом примере у нас были корни, то теперь – логарифмы. Формулы кажутся огромными, но на самом деле их легко реализовать в программе. Чтобы рассчитать сложный процент, формула Excel нужна для одной ячейки – вот и выражаем одно через все остальное. И работает это отлично!
Итак, мы будем использовать такую формулу:
Пример №6.
 У Елены Лениной – 4500$, которые она хочет инвестировать. Она понимает, что может рассчитывать на 50% в год, при этом хочет достичь первой цели – 20000$. Возможно, хочет купить со временем новую машину 🙂
У Елены Лениной – 4500$, которые она хочет инвестировать. Она понимает, что может рассчитывать на 50% в год, при этом хочет достичь первой цели – 20000$. Возможно, хочет купить со временем новую машину 🙂Через сколько времени она достигнет своей цели с условием ежемесячного реинвестирования прибыли? Подставляем числа:
K = 20000$, К0 =4500$, R = 50%, m = 1 месяц
Довольно быстро, должен сказать.
Кстати, опытных инвесторов часто интересует не на сколько, когда и как вырастет капитал. Их больше интересует, когда деньги удвоятся. Другими словами – через сколько они «отобьют» вложения.
Чтобы это узнать, существует универсальное «правило 72». Суть его простая – делите 72 на процентную ставку за месяц (квартал, год). Результат – это и есть тот срок, за который инвестиции удвоятся (в тех же единицах времени, что и ставка доходности).
Пример №7. Инвестор Владимир ВладимирОвич вкладывает деньги под 10% в месяц. Через сколько он отобьет вложения?
Ответ: через 72/10=7.2 месяца.
Вложения под 6% в месяц дают удвоение капитала за год. Под 3% — за 2 года.
———— ↑ к содержанию ↑ ————
Расчет сложных процентов в Excel по формулам
Многие из формул, которые я вам написал, на калькуляторе посчитать не то что неудобно – почти невозможно. Да и зачем это, если есть замечательная программа, о которой пишу чуть ли не в каждой статье 🙂
Например, в статье «Делаем собственный рейтинг ПАММ-счетов» я показал, как с помощью Excel проранжировать ПАММ-счета по нескольким показателям и автоматически найти самые выгодные варианты.
Поэтому я сделал для вас очередной полезный Excel-файлик – Калькулятор сложных процентов с капитализацией. Там вы найдете 5 табличек для расчетов по формулам из этой статьи.
Напоминаю, что мы искали:
- финальный капитал;
- финальный капитал с пополнениями;
- начальный капитал;
- процентную ставку;
- срок достижения инвестиционных целей.

В Калькуляторе сложных процентов эти задачи автоматизированы, используется формула сложных процентов в Excel (все виды), о которых мы говорили в этой статье. Надеюсь, пригодится 🙂
Скачать файл: «Расчет сложных процентов».
На всякий случай записал небольшую видеоинструкцию:
Если у вас нет Экселя или неудобно им пользоваться, можете попробовать поискать в Интернете сайты по запросам «калькулятор сложного процента с реинвестированием», «калькулятор сложного процента с капитализацией» или «калькулятор инвестора сложный процент». Вы найдете множество онлайн-сервисов, выбирайте, какой понравится.
———— ↑ к содержанию ↑ ————
И на этом я прощаюсь. По традиции, несколько вопросов к вам, читатели:)
Первое – как часто вам приходится считать сложный процент? И приходится ли? Лично мне не очень часто, но это потому что я считаю доходность ПАММ-счетов через интервалы – результат почти такой же выходит. Больше нигде применять не приходилось, кроме нескольких пар на втором курсе, когда мы учили «Финансовую математику».
Второе – есть ли у вас какие-то инвестиционные цели? Дойти до энной цифры с энным количеством нулей? Получить определенную доходность? Может, стать рантье? 🙂
Расскажите!
С уважением, Александр Дюбченко
Все статьи блога «Инвестируй в ЭТО»
Понравилась статья? Скажите «спасибо» лайком!
Нужно больше информации? Вот еще 4 статьи для вас:
rt.Уравнение сложных процентов
A = P (1 + r / n) нт
Где:
- A = Начисленная сумма (основная сумма + проценты)
- P = Основная сумма
- I = Сумма процентов
- R = Годовая номинальная процентная ставка в процентах
- r = годовая номинальная процентная ставка в десятичном формате
- r = R / 100
- t = время в годах, 0.
 5 лет считаются как 6 месяцев и т. Д.
5 лет считаются как 6 месяцев и т. Д. - n = количество периодов начисления сложных процентов на единицу t; в КОНЦЕ каждого периода
Формулы и расчеты сложных процентов:
- Рассчитать начисленную сумму (основная сумма + проценты)
- Вычислить основную сумму, найти P как функцию от A
- Вычислить основную сумму, найти P как функцию от I.
- P = I / ((1 + r / n) н. — 1)
- Рассчитать процентную ставку в десятичном виде, решить для r
- Рассчитать процентную ставку в процентах
- Рассчитать время, решить для t
- t = ln (A / P) / n [ln (1 + r / n)], тогда также
- t = [ln (A) — ln (P)] / n [ln (1 + r / n)]
Формулы, где n = 1 (вычисляется один раз за период или единицу t)
- Рассчитать начисленную сумму (основная сумма + проценты)
- Вычислить основную сумму, найти P как функцию от A
- Вычислить основную сумму, найти P как функцию от I.
- Рассчитать процентную ставку в десятичном виде, решить для r
- Рассчитать процентную ставку в процентах
- Рассчитать время, решить для t
- t = ln (A / P) / ln (1 + r), тогда также
- t = [ln (A) — ln (P)] / ln (1 + r)
Формулы непрерывного смешения (n → ∞)
- Рассчитать начисленную сумму (основная сумма + проценты)
- Вычислить основную сумму, найти P как функцию от A
- Вычислить основную сумму, найти P как функцию от I.
 {rt} \]
{rt} \]И, наконец, у вас есть ваша формула непрерывного смешивания.{rt} \]
Дополнительная литература
Древо математики: НЕПРЕРЫВНОЕ СОЕДИНЕНИЕ
Пример расчета
У меня есть инвестиционный счет, размер которого увеличился с 30 000 до 33 000 долларов за 30 месяцев. Если мой местный банк предлагает сберегательный счет с ежедневным начислением сложных процентов (365), какую годовую процентную ставку мне нужно получить от них, чтобы соответствовать доходу, полученному с моего инвестиционного счета?
В калькуляторе выберите «Рассчитать ставку (R)».Калькулятор будет использовать следующее уравнение: r = n [(A / P) 1 / nt — 1] и R = r * 100.
Введите:
Итого P + I (A): 33 000 долларов США
Основная сумма долга (P): 30 000 долл. США
Соединение (n): Ежедневно (365)
Время (t в годах): 2,5 года (2,5 года — 30 месяцев)
Ваш ответ: R = 3,8126% в годТолкование: Вам нужно будет положить 30 000 долларов на сберегательный счет, на котором будет выплачиваться ставка 3.8126% в год и ежедневные начисления процентов, чтобы получать такую же прибыль, как и ваш инвестиционный счет.
Формула и калькулятор будущей стоимостиФормула будущей стоимости помогает рассчитать будущую стоимость инвестиции (FV) для ряда регулярных депозитов с установленной процентной ставкой (r) на несколько лет (t).
Использование формулы требует, чтобы регулярные платежи каждый раз были одной и той же суммы, а итоговая сумма включает проценты, начисляемые в течение срока. означает «во власти»
Пример формулы будущего значения 1
Инвестиции производятся с помощью депозитов в размере 100 долларов США в месяц (вносимых в конце каждого месяца) с процентной ставкой 5%, начисляемой ежемесячно (так, 12 соединений за период).
÷ 0,00416)] nt — 1) ÷ (r / n))]
nt — 1) ÷ (r / n))]
Итого = [100 × (((1 + 0.(120) — 1) ÷ (0,00416))]
Итого = [100 × (0,6470094976
Итого = [15528,23]Таким образом, объем инвестиций через 10 лет составит 15 528,23 долларов США.
Пример формулы будущего значения 2
Физическое лицо решает инвестировать 10 000 долларов в год (вносится в конце каждого года) под 6% годовых, начисляемых ежегодно. Стоимость инвестиции через 5 лет можно рассчитать следующим образом …
PMT = 10000.5 — 1) ÷ 0,06)]
Итого = [10000 × (0,3382255776 ÷ 0,06)]
Итого = [10000 × 5,63709296]
Итого = [56370,9296]Таким образом, наш инвестиционный баланс через 5 лет составляет 56 370,93 долларов США. Это будет включать 50 000 долларов инвестиций и 6 370,93 долларов процентов.
Интерактивная формула будущей стоимости
Воспользуйтесь калькулятором ниже, чтобы показать формулу и результат расчета для выбранных вами цифр. Обратите внимание, что для этого калькулятора в вашем браузере должен быть включен JavaScript.) — 1) ÷)
знак равно А
Если вы хотите получить визуальную разбивку депозитов и процентов с течением времени, попробуйте наш калькулятор сложных процентов.
Реклама
Оцените статью
Пожалуйста, оцените эту статью ниже. Если у вас есть отзывы об этом, пожалуйста, свяжитесь со мной.
BODMAS Explained — Порядок математических операций
Ник Валентайн | Последнее обновление: 16 марта 2019 г.
Когда вам дается сумма, состоящая из двух чисел и одного оператора, вычисление ответа кажется простым (25 × 3 = 75).Но что произойдет, если кто-то добавит еще пару чисел и операторов: (5 + 25 × 3 — 2 = .
 ….)? Какую часть вы делаете в первую очередь? К счастью, существует набор простых правил решения математических сумм. Вот тут-то и пригодится BODMAS.
….)? Какую часть вы делаете в первую очередь? К счастью, существует набор простых правил решения математических сумм. Вот тут-то и пригодится BODMAS.Что такое БОДМАС?
BODMAS — это аббревиатура, обозначающая порядок математических операций. Если сумма содержит несколько чисел и операций, вам нужно знать, какую часть решить в первую очередь, чтобы решить ее в правильном порядке.В противном случае вы получите неправильный ответ.
BODMAS означает
.- B ракетки (любая часть, указанная в скобках, идет первой)
- O rder (операции, содержащие степени или квадратные корни)
- D ivision
- M повторение
- A ddition
- S убирание
Насколько хорошо известен BODMAS?
В 2012 году доктор Питер Прайс, соучредитель веб-сайта Classroom Professor, разместил математический вопрос на своей странице в Facebook.Вот что он спросил:
Вы можете на это ответить?
7-1 x 0 + 3 ÷ 3 =?
Сообщение быстро распространилось по Facebook, более 70000 человек увидели его, а 6000 человек оставили ответы и комментарии. Через 2 недели Питер подвел итоги — результаты, которые его удивили. Только 26% респондентов дали правильный ответ (правильный ответ — 8).
РекламаЕсли учесть, что с психологической точки зрения люди, скорее всего, будут комментировать что-то подобное публично, если они достаточно уверены в своем ответе, чтобы не казаться глупыми, это, похоже, многое говорит о математическом понимании всего населения.В самом деле, это, по-видимому, демонстрирует, что подавляющее большинство людей (вероятно, более 74%) не понимают концепции BODMAS и порядка операций .
Суммы секвенирования: BODMAS
Как часто вы видели, как подобные вопросы ходят на Facebook? Правильный ответ — 12.В арифметике есть два типа компонентов: сами числа и операторы (также называемые операциями), которые говорят вам, что делать с этими числами.
Итак, в сумме 7 x 3 + 5 есть три числа; 7, 3 и 5 и два оператора, умножение (x) и сложение (+).Вы также можете видеть, что эта сумма может дать два разных ответа в зависимости от того, в каком порядке вы используете операторы.
- Если вы умножите семь на три и сложите пять, получится 26.
- Но если вы умножите семь на сумму трех и пяти (восьми), то получите 56.
Итак, как узнать, в каком порядке действовать? Опытные математики знают, что существует определенная иерархия операций и порядок по умолчанию для выполнения основных арифметических операций: сложение, вычитание, умножение и деление).
БОДМАС или ПЕМДАС?
Окончательный порядок операций резюмируется в аббревиатуре BODMAS , что означает скобки, порядок, деление, умножение, сложение, вычитание. Было бы проще, если бы BODMAS был признан во всем мире, но, к сожалению, это не так.
В США это обычно называется PEMDAS (Круглая скобка, Показатель, Умножение, Разделение, Сложение, Вычитание) или PIDMAS (Круглая скобка, Индекс, Деление, Умножение, Сложение, Вычитание). Другие места в мире могут использовать BIDMAS (скобки, указатель, разделение, умножение, сложение, вычитание), в то время как канадцы сидят посередине с BEMDAS (скобки, экспонента, умножение, деление, сложение, вычитание).
Являются ли BODMAS и PEMDAS одинаковыми?
да. Терминология аббревиатуры может быть разной, но последовательность остается прежней. BODMAS и PEMDAS (и другие подобные акронимы) представляют собой порядок, в котором умножение и деление являются одним и тем же шагом (как при сложении и вычитании).
Применение порядка операций
Последовательность операций (будь то BODMAS, PEMDAS, PIDMAS, BIDMAS или BEMDAS) остается прежней:
Шаг 1. Кронштейны
Порядок наивысшего уровня определяется тем, что содержится в скобках.Эти суммы всегда рассчитываются в первую очередь. Но что, если скобок несколько? Таким образом, правило состоит в том, чтобы начинать с самого внутреннего набора и работать вовне. Выполнение каждого вычисления в квадратных скобках должно оставить вам одно число, позволяющее удалить этот набор скобок.
Шаг 2: Заказ или индекс
Все термины Порядок или Индекс относятся к операциям, содержащим степени или индексы, такие как возведение в квадрат или извлечение квадратного корня. Все эти вычисления выполняются вторыми.
Шаги 3 и 4: разделение и умножение
Третий и четвертый этапы, деление и умножение, имеют равный вес и, таким образом, образуют порядок операций третьего уровня, выполняемых одновременно.Важно отметить, что когда две или более операций одного порядка появляются одна за другой, операции должны выполняться слева направо.
Итак, если вы столкнулись с такой суммой, как:
18 ÷ 6 × 4 ÷ 8вы просто работаете слева направо. Восемнадцать на шесть — три, умножение на четыре — двенадцать, деленное на восемь — 1,5.
Шаги 5 и 6: Сложение и вычитание
Опять же, они имеют одинаковый вес. Следовательно, сложение и вычитание образуют порядок операций четвертого и последнего уровня. Третий и четвертый этапы, деление и умножение имеют равный вес и, таким образом, образуют порядок операций третьего уровня, которые выполняются одновременно, снова работая слева направо. Правильно.
Таким образом, после того, как вы выполнили все вычисления «B» и «O / E / I» в указанном порядке, просто работайте слева направо, выполняя любые «D» или «M», как вы их найдете, а затем вернитесь к начало и работайте слева направо над всеми суммами «A» или «S».
Использование BODMAS — пример
Как помогает БОДМАС? Если мы вернемся к нашей первоначальной сумме; 7 х 3 + 5; мы видим, что теперь есть только один ответ. Сначала произведите 7 x 3 как умножение (21), а затем сложите 5, чтобы получить 26.Если бы намерение было другим, тогда необходимо было бы вставить квадратные скобки, таким образом: 7 x (3 + 5), чтобы сложение в квадратных скобках было выполнено первым, чтобы получить 7 x 8 = 56.
Давайте попробуем более сложную сумму, чтобы увидеть всю систему в действии. Чтобы упростить обнаружение и различение, символы деления выделены синим, а дополнения — оранжевым.
А вот и умопомрачительный расчет:
8 6 x (15 + 92) — (37-18) ÷ ((9 + 9.5) — 8)
—————————————
27 + (15 х 3) х ((72-15) х 3,6)Обратите внимание, что у нас есть два вычисления в двойных скобках. Причем вся сумма — дробь. Если у вас двойные скобки, внутренние разрешаются раньше, чем внешние. В случаях, когда у вас есть общее деление типа дроби, суммы вычисляются выше и ниже линии, разрешая общее деление в конце.
Теперь с BODMAS вся эта арифметика становится простой (хотя и несколько трудоемкой).
Работая изнутри наружу, мы сначала решаем все эти внутренние вычисления в квадратных скобках, производя:
8 6 x (15 + 92) — (37-18) ÷ (18,5 — 8)
————————— ————
27 + (15 х 3) х (57 х 3,6)Затем, работая слева направо над и под линией, мы решаем все оставшиеся вычисления в квадратных скобках:
8 6 x 107-19 ÷ 10,5
—————————————
27 + 45 х 205.2Теперь мы обрабатываем оставшуюся операцию Order (8 6 ), чтобы получить:
262144 x 107-19 ÷ 10,5
—————————————
27 + 45 х 205,2Затем мы вычисляем все умножения и деления над и под линией слева направо. Обратите внимание, что верхняя строка содержит неоднозначность, аналогичную той, которую мы встретили в начале. Может ли это быть 262144 x (107-19), что дает 23 068 672?
Однако, используя формулу BODMAS , умножения (262144 x 107 и 45 x 205.2) явно имеют приоритет.
Это дает:
28 049 408 — 19 ÷ 10,5
—————————————
27 + 9234Опять же, без BODMAS остаётся двусмысленность. Однако правила гласят, что разделение имеет приоритет. Итак, подойдем к этому как:
28049408 — (19 ÷ 10,5)
—————————————
27 + 9234Применяя их, мы получаем:
28049408 — 1.8095
—————————————
27 + 9234Наконец, применяя сложение и вычитание, по адресу:
28049406.1905
—————————————
9261Наконец, у нас осталось общее разделение, которое сводится к окончательному ответу (с округлением до трех знаков после запятой):
3028.766
Особые случаи
На самом деле нет никаких исключений из иерархии BODMAS , но есть несколько особых случаев, связанных с порядками или показателями.
В первом случае вы получаете показатель степени внутри части вычисления в квадратных скобках, например:
25 + (5 × 8 2 + 7)
Хотя скобки теоретически имеют приоритет над порядками, в пределах заключенной в квадратные скобки части суммы показатель степени имеет приоритет над всем остальным, поэтому мы решаем это в первую очередь.
25 + (5 × 64 + 7)
Точно так же в скобках умножение теперь имеет приоритет, поэтому:
25 + (320 + 7)
Теперь дополнение, позволяющее отказаться от скобок:
25 + 327
Окончательный ответ: 352
Экспоненты
Есть еще один особый случай, связанный с показателями экспонент.
Просто изредка вы можете встретить расчет, содержащий что-то вроде этого:
7 2 3
Другими словами, семь возведены в степень двойки в кубе.
Только в этом случае мы нарушаем правило слева направо, чтобы работать справа налево или снаружи внутрь.
Сначала разложите куб из двух: 2 x 2 x 2 = 8.Теперь снова переместитесь влево, чтобы вычислить семь в степени восьми. Здесь нам нужно быть осторожными и понимать, что «экспонента» означает, сколько раз использовать базовое число при умножении самого по себе.
Таким образом, при семи в восьмой степени (7 8 ) семь — это «основание», то есть умножаемая величина, а восемь — это показатель степени, сколько раз она используется.
Довольно просто — и я допустил именно эту ошибку в предыдущем черновике этой статьи — повторить базовую операцию 7×7 восемь раз, чтобы получить 40,353,607. НЕПРАВИЛЬНЫЙ!
При этом упускается из виду, что первые семь являются не только основанием, но и первым показателем степени. 7 1 (семь в степени единицы)… Семь.
Таким образом, первое умножение (7×7) дает 7 2 или семь в квадрате. Следовательно, 7 8 можно отобразить как:
7 = семь в степени единицы
7×7 = 49 (семь в степени 2)
49 x 7 = 343 (семь в степени 3)
343 x 7 = 2401 (семь в степени 4)
2401 x 7 = 16807 (семь в степени 5)
16807 x 7 = 117649 (семь в степени 6)
117649 x 7 = 823543 (семь в степени 7)
823543 x 7 = 5764801 (семь в степени 8)
Итак, Окончательный ответ на эту сложную сумму PEDMAS из нескольких операций:5,764,801
Вот как мы это делаем, дамы и господа.
Установка скоб
Из всего этого должно быть ясно несколько вещей. Во-первых, в сложных расчетах вам понадобятся скобки. Скобки — это ваши навигационные путевые точки по сумме.
Во-вторых, неправильное расположение скобок приведет к неправильному ответу. Математика в этом отношении очень неумолима.
Следовательно, и, наконец, сложные суммы должны быть разработаны и нанесены на карту как сложные путешествия. Прежде чем достать свой надежный калькулятор, вам, вероятно, нужно будет набросать всю сумму на бумаге, чтобы убедиться, что все ваши утки (или скобки) хорошо выстроены в ряд, прежде чем вы начнете фактический расчет.
Тест BODMAS
Вы концентрировались? Пришло время выяснить это с помощью небольшого вопроса, предназначенного для проверки вашего понимания BODMAS и порядка операций.
Ответьте на вопрос ниже. Нет никакого приза, кроме права хвастаться высшим классом (ты болван!).
С днем БОДМЫ!
Реклама
Оцените статью
Пожалуйста, оцените эту статью ниже.Если у вас есть отзывы об этом, пожалуйста, свяжитесь со мной.
Определение сложных процентов
Что такое сложный процент?
Сложные проценты (или сложные проценты) — это проценты по ссуде или депозиту, рассчитываемые как на основе первоначальной основной суммы, так и накопленных процентов за предыдущие периоды.Считается, что сложный процент возник в Италии 17-го века, сложный процент можно рассматривать как «процент на процент», и он заставляет сумму расти быстрее, чем простой процент, который рассчитывается только на основную сумму.
Ставка, по которой начисляются сложные проценты, зависит от частоты начисления сложных процентов, так что чем больше количество периодов начисления сложных процентов, тем больше сложный процент. Таким образом, сумма сложных процентов, начисленных на 100 долларов США с начислением 10% годовых, будет ниже, чем сумма сложных процентов, начисленных на 100 долларов США с начислением 5% годовых в течение того же периода времени.Поскольку эффект процентной ставки может приносить все более положительную прибыль на основе первоначальной основной суммы, ее иногда называют «чудом сложных процентов».
Ключевые выводы
- Сложные проценты (или сложные проценты) — это проценты, начисляемые на первоначальную основную сумму, которая также включает все накопленные проценты за предыдущие периоды по депозиту или ссуде.
- Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная до количества составных периодов минус один.
- Проценты могут начисляться по любому заданному графику периодичности, от непрерывного до ежедневного или ежегодного.
- При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение.
Общие сведения о сложных процентах
Расчет сложных процентов
Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная на количество составных периодов минус один.Затем из полученной стоимости вычитается общая начальная сумма ссуды.
Кэти Керпель {Copyright} Investopedia, 2019.Формула расчета сложных процентов:
- Сложные проценты = общая сумма основной суммы долга и процентов в будущем (или будущая стоимость) минус текущая сумма основного долга (или приведенная стоимость)
= [P (1 + i ) n ] — P
= P [(1 + i ) n — 1]
Где:
P = основной
i = номинальная годовая процентная ставка в процентах
n = количество периодов начисления сложных процентов
Возьмите трехлетнюю ссуду в размере 10 000 долларов США под 5% годовых.Какая будет сумма процентов? В этом случае это будет:
10 000 долл. США [(1 + 0,05) 3 — 1] = 10 000 [1,157625 — 1] = 1 576,25 доллара
Рост сложных процентов
Используя приведенный выше пример, поскольку сложные проценты также учитывают накопленные проценты за предыдущие периоды, сумма процентов не будет одинаковой для всех трех лет, как это было бы с простыми процентами. При этом общая сумма процентов, подлежащих выплате за трехлетний период по этой ссуде, составляет 1576 долларов США.25, проценты, подлежащие выплате в конце каждого года, показаны в таблице ниже.
Периоды начисления процентов
При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение. Основное правило состоит в том, что чем больше количество периодов начисления сложных процентов, тем больше сумма сложных процентов.
Следующая таблица демонстрирует разницу, которую может составить количество периодов начисления сложных процентов для ссуды в размере 10 000 долларов США с годовой процентной ставкой 10% в течение 10-летнего периода.
Сложные проценты могут значительно повысить доходность инвестиций в долгосрочной перспективе. В то время как вклад в размере 100 000 долларов, который получает 5% простых годовых процентов, принесет 50 000 долларов в общей сумме процентов за 10 лет, годовые сложные проценты в размере 5% на 10 000 долларов составят 62 889,46 долларов США за тот же период. Если бы период начисления сложных процентов вместо этого выплачивался ежемесячно в течение того же 10-летнего периода под 5% сложных процентов, общая сумма процентов вырастала бы до 64 700,95 долларов.
Расчет компаундирования в Excel
Если с тех пор, как вы учились в математике, прошло некоторое время, не бойтесь: есть удобные инструменты, которые помогут сложить числа.Многие калькуляторы (как карманные, так и компьютерные) имеют функции экспоненты, которые можно использовать для этих целей. Если возникают более сложные сложные задачи, они могут быть выполнены с помощью Microsoft Excel тремя различными способами.
- Первый способ рассчитать сложные проценты — это умножить новый баланс каждого года на процентную ставку. Предположим, вы вкладываете 1000 долларов на сберегательный счет с годовой процентной ставкой 5% и хотите рассчитать остаток через пять лет.В Microsoft Excel введите «Год» в ячейку A1 и «Баланс» в ячейку B1. Введите годы от 0 до 5 в ячейки с A2 по A7. Баланс за год 0 составляет 1000 долларов, поэтому вы должны ввести «1000» в ячейку B2. Затем введите «= B2 * 1,05» в ячейку B3. Затем введите «= B3 * 1.05» в ячейку B4 и продолжайте делать это, пока не дойдете до ячейки B7. В ячейке B7 вычисление будет «= B6 * 1,05». Наконец, вычисленное значение в ячейке B7 — 1276,28 доллара — это остаток на вашем сберегательном счете через пять лет. Чтобы найти значение сложных процентов, вычтите 1000 долларов из 1276 долларов.n) — P. »В третьей строке модуля введите« Конечная функция ». Вы создали макрос функции для расчета сложной процентной ставки. Продолжая с той же таблицы Excel выше, введите« Сложный процент »в ячейку A6 и введите «= Compound_Interest (B1, B2, B3).» Это дает вам значение 276,28 доллара США, что согласуется с первыми двумя значениями.
Использование других калькуляторов
Как упоминалось выше, в Интернете предлагается ряд бесплатных калькуляторов сложных процентов, и многие портативные калькуляторы также могут выполнять эти задачи.
- Бесплатный калькулятор сложных процентов, предлагаемый на сайте Financial-Calculators.com, прост в использовании и предлагает выбор частоты от дня до года. Он включает в себя возможность выбора непрерывного начисления процентов, а также позволяет вводить фактические календарные даты начала и окончания. После ввода необходимых данных расчета результаты показывают заработанные проценты, будущую стоимость, годовую процентную доходность (APY), которая является мерой, включающей начисление сложных процентов и ежедневные проценты.
- Investor.gov, веб-сайт, управляемый Комиссией по ценным бумагам и биржам США (SEC), предлагает бесплатный онлайн-калькулятор сложных процентов. Калькулятор довольно прост, но он позволяет вводить ежемесячные дополнительные депозиты основному лицу, что полезно для расчета доходов, когда вкладываются дополнительные ежемесячные сбережения.
- Бесплатный онлайн-калькулятор процентов с несколькими дополнительными функциями доступен на TheCalculatorSite.com. Этот калькулятор позволяет производить расчеты для различных валют, учитывать ежемесячные депозиты или снятия, а также автоматически рассчитывать ежемесячные депозиты или снятия с поправкой на инфляцию.
Частота смешивания
Проценты могут быть увеличены по любому заданному графику периодичности, от ежедневного до ежегодного. Существуют стандартные графики частоты начисления сложных процентов, которые обычно применяются к финансовым инструментам.
Обычно для сберегательного счета в банке используется ежедневный график начисления сложных процентов. Для компакт-диска типичными графиками частоты начисления сложных процентов являются ежедневные, ежемесячные или полугодовые; для счетов денежного рынка — часто ежедневно. Для жилищных ипотечных ссуд, ссуд под залог недвижимости, ссуд для личного бизнеса или счетов по кредитным картам обычно применяется ежемесячный график начисления сложных процентов.
Также могут быть разные временные рамки, в течение которых начисленные проценты фактически зачисляются на существующий баланс. Проценты по счету могут начисляться ежедневно, но только ежемесячно. Только когда проценты фактически зачисляются или добавляются к существующему балансу, они начинают приносить дополнительные проценты на счет.
Некоторые банки также предлагают так называемое непрерывное начисление сложных процентов, которое увеличивает процентную ставку к основной сумме в каждый возможный момент.С практической точки зрения, это не намного больше, чем ежедневное начисление сложных процентов, если только вы не хотите вкладывать деньги и снимать их в тот же день.
Более частое начисление сложных процентов выгодно инвестору или кредитору. Для заемщика все наоборот.
Временная стоимость денег Возмещение
Понимание временной стоимости денег и экспоненциального роста, создаваемого сложным капиталом, важно для инвесторов, стремящихся оптимизировать свои доходы и распределение богатства.
Формула для получения будущей стоимости (FV) и текущей стоимости (PV) выглядит следующим образом:
FV = PV (1 + i) n и PV = FV / (1 + i) n
Например, будущая стоимость 10 000 долларов США составит 5% годовых в течение трех лет:
= 10 000 долл. США (1 + 0,05) 3
= 10 000 долл. США (1 157 625 долл. США)
= 11 576,25 долл. США
Приведенная стоимость 11 576,25 долларов США со скидкой 5% на три года:
= 11 576 долларов США.25 / (1 + 0,05) 3
= 11 576,25 долл. США / 1 157 625 долл. США
= 10 000 долл. США
Обратное значение 1,157625, равное 0,8638376, в данном случае является коэффициентом дисконтирования.
Рассмотрение по «Правилу 72»
Так называемое Правило 72 рассчитывает приблизительное время, в течение которого инвестиции удвоятся при заданной норме прибыли или процентах «i», и определяется выражением (72 / i). Его можно использовать только для годового начисления процентов.
Например, инвестиция с годовой доходностью 6% удвоится через 12 лет.Таким образом, инвестиции с годовой доходностью 8% за девять лет увеличатся вдвое.
Совокупный годовой темп роста (CAGR)
Совокупный годовой темп роста (CAGR) используется для большинства финансовых приложений, которые требуют расчета единого темпа роста за период времени.
Допустим, ваш инвестиционный портфель вырос с 10 000 до 16 000 долларов за пять лет; что такое CAGR? По сути, это означает, что PV = — 10 000 долларов США, FV = 16 000 долларов США и nt = 5, поэтому переменная «i» должна быть вычислена.Используя финансовый калькулятор или Excel, можно показать, что i = 9,86%.
Согласно соглашению о движении денежных средств, ваши первоначальные инвестиции (PV) в размере 10 000 долларов США отображаются с отрицательным знаком, поскольку они представляют собой отток средств. Чтобы найти «i» в приведенном выше уравнении, PV и FV обязательно должны иметь противоположные знаки.
CAGR Реальные приложения
CAGR широко используется для расчета доходности за периоды времени для акций, паевых инвестиционных фондов и инвестиционных портфелей.CAGR также используется для определения того, превышал ли управляющий паевым инвестиционным фондом или управляющий портфелем рыночную норму прибыли в течение определенного периода времени. Если, например, рыночный индекс обеспечил общую доходность 10% за пятилетний период, но управляющий фондом получил только 9% годовой прибыли за тот же период, это означает, что он отстал от рынка.
CAGR также можно использовать для расчета ожидаемых темпов роста инвестиционных портфелей в течение длительных периодов времени, что полезно для таких целей, как накопление средств на пенсию.Рассмотрим следующие примеры:
Пример 1: Не склонный к риску инвестор доволен скромной 3% годовой доходностью своего портфеля. Таким образом, ее нынешний портфель в 100 000 долларов через 20 лет вырастет до 180 611 долларов. Напротив, толерантный к риску инвестор, ожидающий годовой доходности своего портфеля в размере 6%, через 20 лет увидит, что 100 000 долларов США вырастут до 320 714 долларов США.
Пример 2: CAGR можно использовать для оценки того, сколько нужно убрать, чтобы сэкономить для конкретной цели.Паре, которая хотела бы сэкономить 50 000 долларов в течение 10 лет на первоначальный взнос за кондоминиум, потребуется экономить 4 165 долларов в год, если они предполагают, что годовая прибыль (CAGR) составит 4% от своих сбережений. Если они готовы пойти на небольшой дополнительный риск и рассчитывать на среднегодовой темп роста 5%, им нужно будет экономить 3 975 долларов в год.
Пример 3: CAGR также можно использовать для демонстрации преимуществ инвестирования в более раннем, чем в более позднем возрасте. Если цель состоит в том, чтобы сэкономить 1 миллион долларов к выходу на пенсию в возрасте 65 лет, исходя из среднегодового роста в 6%, 25-летнему человеку нужно будет откладывать 6 462 доллара в год для достижения этой цели.С другой стороны, 40-летнему человеку нужно будет сэкономить 18 227 долларов, или почти в три раза больше, чтобы достичь той же цели.
- CAGR также часто возникают в экономических данных. Вот пример: ВВП на душу населения в Китае увеличился с 193 долларов в 1980 году до 6091 долларов в 2012 году. Каков годовой рост ВВП на душу населения за этот 32-летний период? Темп роста «i» в данном случае составляет впечатляющие 11,4%.
Плюсы и минусы компаундирования
Хотя магия сложного капитала привела к апокрифической истории о том, что Альберт Эйнштейн назвал его восьмым чудом света или величайшим изобретением человека, сложный процесс также может работать против потребителей, у которых есть ссуды с очень высокими процентными ставками, например, задолженность по кредитной карте.Баланс кредитной карты в размере 20 000 долларов США с ежемесячной процентной ставкой 20% приведет к общей сумме сложных процентов в размере 4 388 долларов США за год или около 365 долларов США в месяц.
С положительной стороны, магия начисления сложных процентов может работать вам на пользу, когда дело касается ваших инвестиций, и может быть мощным фактором создания богатства. Экспоненциальный рост за счет сложных процентов также важен для смягчения факторов, разрушающих благосостояние, таких как рост стоимости жизни, инфляция и снижение покупательной способности.
Паевые инвестиционные фонды предлагают инвесторам один из самых простых способов воспользоваться преимуществами сложных процентов. Решение реинвестировать дивиденды, полученные от паевого инвестиционного фонда, приводит к покупке большего количества акций фонда. Со временем накапливается больше сложных процентов, и цикл покупки большего количества акций будет продолжать способствовать росту стоимости инвестиций в фонд.
Рассмотрим инвестиционный паевой инвестиционный фонд, открытый с начальными 5000 долларов и ежегодным приростом в 2400 долларов. При средней годовой доходности 12% за 30 лет будущая стоимость фонда составляет 798 500 долларов.Сложный процент — это разница между денежными средствами, внесенными в инвестиции, и фактической будущей стоимостью инвестиций. В этом случае при внесении 77 000 долларов США или совокупного взноса в размере всего 200 долларов США в месяц в течение 30 лет сложные проценты составляют 721 500 долларов США от будущего баланса.
Конечно, доходы от сложных процентов подлежат налогообложению, если только деньги не находятся на счете, защищенном от налогов; обычно он облагается налогом по стандартной ставке, установленной для налоговой категории налогоплательщика.
Инвестиции со сложными процентами
Инвестор, который выбирает план реинвестирования в рамках брокерского счета, по сути, использует возможность начисления сложных процентов во все, что он инвестирует.Инвесторы также могут получить сложный процент при покупке облигации с нулевым купоном. Традиционные выпуски облигаций обеспечивают инвесторам периодические выплаты процентов на основе первоначальных условий выпуска облигаций, и, поскольку они выплачиваются инвестору в форме чека, проценты не складываются.
Бескупонные облигации не высылают инвесторам процентные чеки; вместо этого облигации этого типа приобретаются со скидкой по сравнению с их первоначальной стоимостью и со временем растут. Эмитенты бескупонных облигаций используют возможность начисления сложных процентов для увеличения стоимости облигации, чтобы она достигла своей полной цены к моменту погашения.
Компаундирование также может работать на вас при выплате кредита. Например, если вы будете выплачивать половину ипотечного платежа дважды в месяц вместо того, чтобы вносить полный платеж один раз в месяц, это сократит ваш период амортизации и сэкономит вам значительную сумму процентов.
Кстати о займах…
Информация о начислении процентов
Закон о правде в кредитовании (TILA) требует, чтобы кредиторы раскрывали потенциальным заемщикам условия займа, включая общую сумму процентов в долларах, подлежащую выплате в течение срока займа, а также то, начисляются ли проценты простым или сложным образом.
Другой метод — сравнить процентную ставку по ссуде с ее годовой процентной ставкой (APR), которую TILA также требует от кредиторов. Годовая процентная ставка конвертирует финансовые расходы по вашему кредиту, которые включают все проценты и комиссии, в простую процентную ставку. Существенная разница между процентной ставкой и годовой процентной ставкой означает один или оба из двух сценариев: в вашем ссуде используются сложные проценты или в дополнение к процентам он включает огромные комиссии по ссуде. Даже когда речь идет о ссуде одного и того же типа, диапазон годовых может сильно различаться между кредиторами в зависимости от комиссий финансового учреждения и других расходов.
Вы заметите, что процентная ставка, которую вы взимаете, также зависит от вашего кредита. Ссуды, предлагаемые тем, у кого есть отличная кредитоспособность, имеют значительно более низкие процентные ставки, чем те, которые взимаются с лиц с плохой кредитной историей.
Часто задаваемые вопросы
Что такое простое определение сложных процентов?
Сложные проценты относятся к явлению, при котором проценты, связанные с банковским счетом, ссудой или инвестициями, со временем растут экспоненциально, а не линейно.Ключом к пониманию концепции является слово «составной». Предположим, вы инвестируете 100 долларов в бизнес, который ежегодно выплачивает вам 10% дивидендов. У вас есть выбор: вложить эти дивиденды в наличные или реинвестировать эти выплаты в дополнительные акции. Если вы выберете второй вариант, реинвестируя дивиденды и сложив их вместе с вашими первоначальными инвестициями в 100 долларов, то получаемая вами прибыль со временем начнет расти.
Кому выгодны сложные проценты?
Проще говоря, сложные проценты приносят пользу инвесторам, но значение слова «инвесторы» может быть довольно широким.Банки, например, получают выгоду от сложных процентов, когда ссужают деньги и реинвестируют полученные проценты в выдачу дополнительных ссуд. Вкладчики также извлекают выгоду из сложных процентов, когда они получают проценты по своим банковским счетам, облигациям или другим инвестициям. Важно отметить, что, хотя термин «сложные проценты» включает слово «проценты», эта концепция применяется за пределами ситуаций, в которых обычно используется слово «проценты», таких как банковские счета и ссуды.
Могут ли сложные проценты сделать вас богатым?
да.Фактически, сложные проценты, возможно, являются самой мощной из когда-либо задуманных сил для создания богатства. Есть записи о купцах, кредиторах и различных бизнесменах, которые использовали сложные проценты, чтобы разбогатеть буквально на тысячи лет. Например, в древнем городе Вавилон глиняные таблички использовались более 4000 лет назад для обучения студентов математике сложных процентов.
В наше время Уоррен Баффет стал одним из самых богатых людей в мире благодаря бизнес-стратегии, которая предусматривала усердное и терпеливое увеличение прибыли от его инвестиций в течение длительных периодов времени.Вполне вероятно, что в той или иной форме люди будут использовать сложные проценты для создания богатства в обозримом будущем.
Формула сложного процента — Обзор, как рассчитать, пример
Что такое формула сложного процента?
Для начала важно понять, что такое сложные проценты. Сложные проценты вычитаются из первоначальной или основной суммы кредита или депозита плюс уже начисленные проценты. Формула сложных процентов — это способ определения таких сложных процентов.
Сложные проценты, начисляемые за период действия кредита Потребительский кредит Потребительский кредит — это кредит, предоставляемый потребителям для финансирования определенных видов расходов. Это может быть любой вид ссуды, предоставленной потребителю кредитором. Ссуда может быть обеспеченной (обеспеченной активами заемщика) или необеспеченной, либо депозит является непогашенным. Как он накапливается, зависит от того, как часто он накапливается. Сложные проценты будут тем выше, чем больше периодов начисления сложных процентов.Что именно это значит? Если, например, ссуда в размере 1000 долларов США предоставляется с полугодовой процентной ставкой сложного процента в размере 2%, она будет генерировать больше начисленных сложных процентов, чем та же сумма ссуды, которая составляет 4% годовых.
Резюме:- Сложные проценты основаны на сумме основной суммы ссуды или депозита — и процентной ставки, — которые начисляются в зависимости от того, как часто ссуда складывается: как правило, начисление сложных процентов происходит либо ежегодно, раз в полгода или ежеквартально.
- Формула сложных процентов — это способ определения сложных процентов.
- Сложные проценты ценны для тех, кто делает вклады, потому что это дополнительный доход для них, чем дольше депозит остается без снятия средств. Это ценно для кредиторов, потому что представляет собой дополнительный доход, полученный от ссудных денег.
Как рассчитать сложные проценты
Формула сложных процентов выглядит следующим образом:
Где:
- T = Всего начислено, включая проценты
- PA = Основная сумма сумма
- roi = Годовая процентная ставка для суммы, заимствованной или депонированной
- t = Сколько раз в год процентные ставки складываются
- y = Количество лет, в течение которых основная сумма была взята или депонирована
Практический пример
Давайте добавим некоторые числа в приведенную выше формулу, чтобы было понятнее.В этом примере предположим, что предлагается заем в размере 1000 долларов США с процентной ставкой Процентная ставка Процентная ставка относится к сумме, взимаемой кредитором с заемщика за любую форму предоставленного долга, обычно выраженную в процентах от основной суммы долга. 5%, которая начисляется каждые полгода. Если кредит будет продлен на пять лет, каков будет остаток на выплату?
Через пять лет общая сумма долга составит 1 280,08 долларов. Расчет будет работать таким же образом, когда речь идет о сумме в 1000 долларов, внесенной в банк, получающий такие же начисленные проценты.Через пять лет общая сумма будет оценена в 1280,08 долларов.
Следует отметить, что при решении только для сложных процентов необходимо вычесть основную сумму ссуды или депозита из общей суммы.
Сложные проценты имеют большое значение для тех, кто вложил деньги или сделал инвестиции, потому что они позволяют им получать увеличивающуюся сумму дохода от первоначальных инвестиций. Это ценно для кредиторов Ведущие банки США По данным Федеральной корпорации по страхованию вкладов США, по состоянию на февраль 2014 года в США насчитывалось 6799 коммерческих банков, застрахованных FDIC.Центральным банком страны является Федеральный резервный банк, который появился после принятия Закона о Федеральной резервной системе в 1913 году, поскольку он добавляет дополнительный доход к сумме ссуды заемщику.
Ссылки по теме
CFI предлагает сертификацию финансового моделирования и оценки (FMVA) ™ FMVA®. Присоединяйтесь к более чем 850 000 студентов, которые работают в таких компаниях, как Amazon, JP Morgan и программа сертификации Ferrari, для тех, кто хочет сделать карьеру следующим образом уровень.Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие ресурсы CFI:
- Годовая процентная доходность Годовая процентная доходность Годовая процентная доходность (APY) — это нормализованная процентная ставка, основанная на периоде начисления сложных процентов в один год. APY обеспечивает стандартизированное представление базовых процентных ставок финансовых продуктов.
- Эффективная годовая процентная ставка Эффективная годовая процентная ставка Эффективная годовая процентная ставка (EAR) — это процентная ставка, которая корректируется с учетом начисления сложных процентов за определенный период.Проще говоря, эффективные
- Непрерывно начисляемые проценты Непрерывно начисляемые проценты Непрерывно начисляемые проценты — это проценты, которые начисляются на первоначальную основную сумму, а также на все проценты, заработанные на других процентах. Идея состоит в том, что принципал будет получать проценты в любой момент времени, а не дискретно в определенные моменты времени.
- Процентный доходПроцентный доходПроцентный доход — это сумма, выплачиваемая предприятию за предоставление его денег в кредит или за предоставление другому предприятию возможности использовать свои средства.В более широком смысле процентный доход — это сумма денег инвестора, которую он вкладывает в инвестицию или проект.
Формула с примерами и практическими задачами. Как работает формула
Сложные проценты — отличная вещь, когда вы их зарабатываете! Сложные проценты — это когда банк выплачивает проценты как на основную сумму (первоначальную сумму денег), так и на проценты, уже заработанные на счете.
Для расчета сложных процентов используйте приведенную ниже формулу.В формуле A представляет собой окончательную сумму на счете после t лет, сложенную n раз при процентной ставке r с начальной суммой p.
Эта страница посвящена пониманию формулы сложных процентов; Если вы хотите глубже понять, как работают сложные проценты, и изучить некоторые примеры из реального мира, прочтите нашу статью здесь.
Задача 1
Если у вас есть банковский счет с основной суммой в 1000 долларов, и ваш банк взимает проценты дважды в год по ставке 5%, сколько денег у вас будет на вашем счете в конце года?
Количество денегЗадача 2
Если вы открываете банковский счет с 10 000 долларов, и ваш банк ежеквартально взимает проценты по ставке 8%, сколько денег у вас будет на конец года? (предположим, что вы не добавляете и не снимаете деньги со счета)
Количество денегЗадача 3
Первая кредитная карта, которую вы получили, списания 12.49% процентов своим клиентам и компаундам, которые начисляют проценты ежемесячно. В течение одного дня после получения первой кредитной карты вы максимально исчерпываете кредитный лимит, потратив 1200 долларов США. Если вы больше ничего не покупаете по карте и не производите никаких платежей, сколько денег вы должны компании через 6 месяцев?
Конечная сумма после смешиванияПримечание: , поскольку продолжительность составляет полгода, значение т. равно ½.
6 месяцев — это половина года, и т. в формуле сложных процентов измеряется годами.Задача 4
Вы выигрываете в лотерею и получаете 1 000 000 долларов. Вы решаете, что хотите вложить все деньги на сберегательный счет.{60} \\ A = 1 348 850,15 $ $$
Я бы выбрал вариант №1План 2
Банк дает вам 12% процентную ставку и начисляет проценты каждые 2 месяца .{30} \\ A = 1 811 361,58 долл. США $$
Я бы выбрал вариант №2Вопрос: Через 5 лет, какой план принесет вам больше денег.
Калькулятор сложных процентов
Входы Текущий директор: $ Ежегодное добавление: $ Годы расти: Процентная ставка: % Сложные проценты раз (а) ежегодно Внести дополнения в Начало конец каждого периода начисления сложных процентов Результаты Будущая стоимость: $ Формула сложных процентов
Сложные проценты — это означает, что проценты, которые вы зарабатываете каждый год, добавляются к вашей основной сумме, так что баланс не просто растет, он растет с возрастающей скоростью — это одна из самых полезных концепций в финансах.
 12=0.88638487 раз). Иными словами, реальная (сложная, эффективная) процентная ставка составляет примерно 12,7% при начислении (при удержании — примерно 11,4%). И т. д. Впрочем, если речь о кредите, реальный процент надо считать не «удерживаемым», а «начисляемым», поскольку он первым делом НАЧИСЛЯЕТСЯ на сумму долга (ПРИБАВЛЯЕТСЯ к ней), а не вычитается из чего-то там еще. То есть, если вы одолжили деньги под 1% в месяц, то годовая цена кредита — около 12,7% в год, а не 12% и уж тем паче не 11,4%.
12=0.88638487 раз). Иными словами, реальная (сложная, эффективная) процентная ставка составляет примерно 12,7% при начислении (при удержании — примерно 11,4%). И т. д. Впрочем, если речь о кредите, реальный процент надо считать не «удерживаемым», а «начисляемым», поскольку он первым делом НАЧИСЛЯЕТСЯ на сумму долга (ПРИБАВЛЯЕТСЯ к ней), а не вычитается из чего-то там еще. То есть, если вы одолжили деньги под 1% в месяц, то годовая цена кредита — около 12,7% в год, а не 12% и уж тем паче не 11,4%. На самом деле проценты — это плата за заем денег, обычно это процент, взимаемый с основной суммы в течение года.
На самом деле проценты — это плата за заем денег, обычно это процент, взимаемый с основной суммы в течение года. Вот несколько примеров формулы:
Вот несколько примеров формулы: Рассел, Деб. (2020, 26 августа). Что такое сложный процент? Формула, определение и примеры. Получено с https://www.oughttco.com/what-is-compound-interest-3863068 Russell, Deb. «Что такое сложный процент? Формула, определение и примеры». ThoughtCo. https://www.oughttco.com/what-is-compound-interest-3863068 (по состоянию на 15 февраля 2021 г.).
Рассел, Деб. (2020, 26 августа). Что такое сложный процент? Формула, определение и примеры. Получено с https://www.oughttco.com/what-is-compound-interest-3863068 Russell, Deb. «Что такое сложный процент? Формула, определение и примеры». ThoughtCo. https://www.oughttco.com/what-is-compound-interest-3863068 (по состоянию на 15 февраля 2021 г.).
 Но я этого делать не буду, так как ПАММ-счета удобнее всего анализировать через среднемесячную доходность.
Но я этого делать не буду, так как ПАММ-счета удобнее всего анализировать через среднемесячную доходность. Соответственно, капитал бы вырос до 35000$. А с учетом сложного процента – на целых 106 тысяч! Теперь разница ощущается очень сильно.
Соответственно, капитал бы вырос до 35000$. А с учетом сложного процента – на целых 106 тысяч! Теперь разница ощущается очень сильно. Реинвест – каждый квартал.
Реинвест – каждый квартал. У Елены Лениной – 4500$, которые она хочет инвестировать. Она понимает, что может рассчитывать на 50% в год, при этом хочет достичь первой цели – 20000$. Возможно, хочет купить со временем новую машину 🙂
У Елены Лениной – 4500$, которые она хочет инвестировать. Она понимает, что может рассчитывать на 50% в год, при этом хочет достичь первой цели – 20000$. Возможно, хочет купить со временем новую машину 🙂
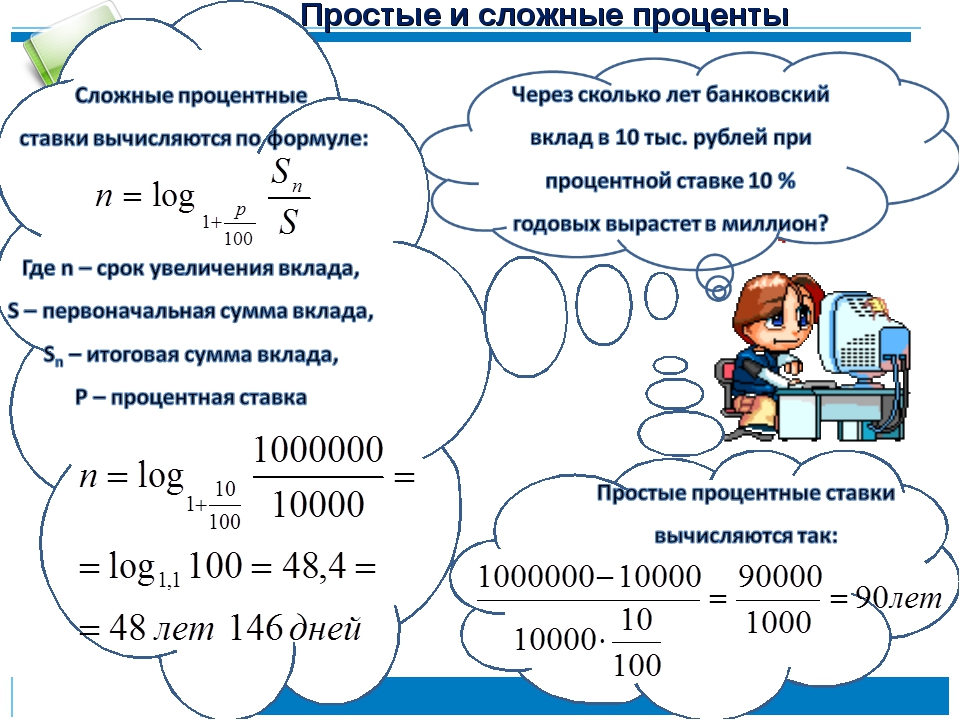 5 лет считаются как 6 месяцев и т. Д.
5 лет считаются как 6 месяцев и т. Д. {rt} \]
{rt} \] nt — 1) ÷ (r / n))]
nt — 1) ÷ (r / n))]  ….)? Какую часть вы делаете в первую очередь? К счастью, существует набор простых правил решения математических сумм. Вот тут-то и пригодится BODMAS.
….)? Какую часть вы делаете в первую очередь? К счастью, существует набор простых правил решения математических сумм. Вот тут-то и пригодится BODMAS.