Процентные ставки простые и сложные: Финансовая грамотность | 7.5.1. Способы начисления процентов. Простые и сложные проценты

Окт 21 2019

Содержание

Страница не найдена

Согласие на обработку персональных данных

Настоящим в соответствии с Федеральным законом № 152-ФЗ «О персональных данных» от 27.07.2006 года свободно, своей волей и в своем интересе выражаю свое безусловное согласие на обработку моих персональных данных АНО ДПО «ИНСТИТУТ СОВРЕМЕННОГО ОБРАЗОВАНИЯ» (ОГРН 1143600000290, ИНН 3666999768), зарегистрированным в соответствии с законодательством РФ по адресу:
УЛ. КАРЛА МАРКСА, ДОМ 67, 394036 ВОРОНЕЖ ВОРОНЕЖСКАЯ ОБЛАСТЬ, Россия (далее по тексту — Оператор). Персональные данные — любая информация, относящаяся к определенному или определяемому на основании такой информации физическому лицу.
Настоящее Согласие выдано мною на обработку следующих персональных данных:
— Телефон.

Согласие дано Оператору для совершения следующих действий с моими персональными данными с использованием средств автоматизации и/или без использования таких средств: сбор, систематизация, накопление, хранение, уточнение (обновление, изменение), использование, обезличивание, а также осуществление любых иных действий, предусмотренных действующим законодательством РФ как неавтоматизированными, так и автоматизированными способами.

Данное согласие дается Оператору для обработки моих персональных данных в следующих целях:
— предоставление мне услуг/работ;
— направление в мой адрес уведомлений, касающихся предоставляемых услуг/работ;
— подготовка и направление ответов на мои запросы;
— направление в мой адрес информации, в том числе рекламной, о мероприятиях/товарах/услугах/работах Оператора.

Настоящее согласие действует до момента его отзыва путем направления соответствующего уведомления на электронный адрес [email protected]. В случае отзыва мною согласия на обработку персональных данных Оператор вправе продолжить обработку персональных данных без моего согласия при наличии оснований, указанных в пунктах 2 – 11 части 1 статьи 6, части 2 статьи 10 и части 2 статьи 11 Федерального закона №152-ФЗ «О персональных данных» от 27.06.2006 г.

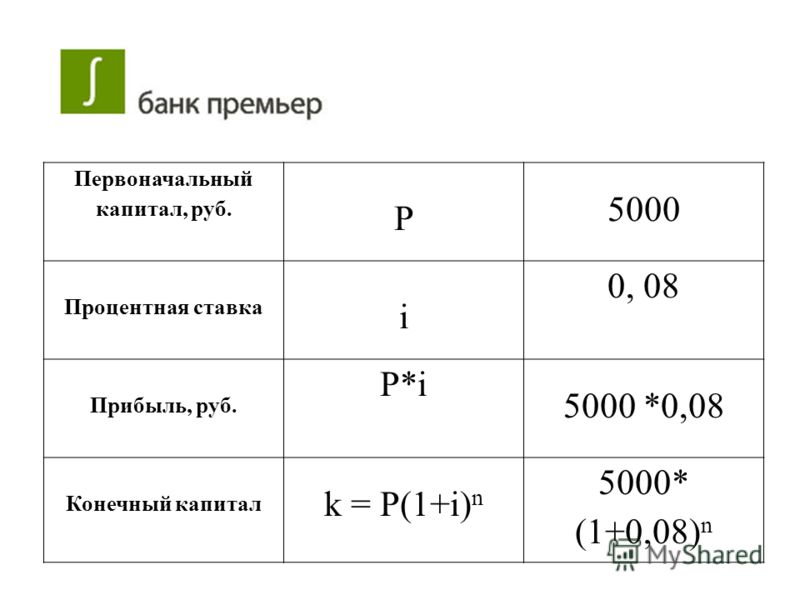
Сложные проценты на примерах

Задачи на сложные проценты решаются в достаточно быстрый способ при знании нескольких простых формул. Часть из них касается начислений по вкладу или кредиту, когда те осуществляются через определенные промежутки времени . Также сложные проценты используют в задачах химии, медицины и ряде других сфер.

ФОРМУЛЫ СЛОЖНЫХ ПРОЦЕНТОВ

В случае размещения вкладов с капитализацией процентов на годы конечная сумма депозита определяется формулой
Здесь P – первоначальный взнос, r – процентная ставка, n – количество лет. По сложным процентам работают банки, инвестиционные фонды, страховые компании. Распространенные за рубежом, а теперь и в Украине — пенсионные фонды и фонды страхования жизни работают по схеме сложных процентов.
При размещении вкладов с капитализацией процентов ежеквартально формула сложных процентов будет выглядеть
где q – количество полных кварталов.
При капитализации процентов ежемесячно применяют следующую формулу для вычислений
где s – количество месяцев существования соглашения.
Последний случай, непрерывное начисление процентов, когда сложные проценты начисляются ежедневно, рассчитывают по формуле
где m – количество дней.
Страхование жизни и откладывания пенсий исчисляют сложными формулами, кроме начисления сложных процентов ежегодно осуществляются необходимые взносы.
Рассмотрим два случая накопления. Мужчина откладывает 5000 грн. в течение 20 лет. За это время он отложит
20*5000=100000 (грн).
При откладывании в накопительные фонды с годовой ставкой 13%, за первый год сумма возрастет до
5000*(1+13/100)=5650 (грн).
В следующем году человек в данной суммы добавляет еще 5000 грн. В результате, за второй год сумма увеличится
(5650+5000)*(1+0,13)=12034.50 (грн) .
Продолжая подобные вычисления, в конце срока получим сумму размером 457349,58 грн.
Поверьте — ошибок при исчислении форуме, большое значение набегает за счет сложных процентов. Сомнительным остается только история изменения платежеспособности гривны через 20 лет. Учитывая политику государства вкладывать деньги в такие фонды люди не спешат, однако за рубежом практика откладывания денег распространена, правда процентные ставки намного ниже.

Рассмотрим распространенные задачи на сложные проценты.

Пример 1. Вкладчик положил на депозит $ 3000 под 9% годовых на 10 лет. Какая сумма аккумулируется конце 10-го года при годовой капитализации? На сколько вырастет сумма по сравнению с первоначальным взносом?

Решение: Применяем формулу сложных процентов для нахождения суммы в конце срока

Чтобы ответить на второй вопрос, от значения 7102,09 вычитаем сумму вклада.

Разница составляет 4102 доллара.

Пример 2. Инвестор вложил 7000 грн под 10% годовых при условии начисления сложных процентов ежеквартально. Какую сумму он получит через 8 лет?

Решение: Применяем 2 формулу сложных процентов. Находим количество кварталов
8*4=32.
и подставляем в формулу

Школьные задачи на сложные проценты

Например, возьмем задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир «Аглгебра». (Номер в скобках)

Задача 1. (556) Костюм стоил 600 грн. После того как цена была снижена дважды, он стал стоить 432 грн., Причем процент снижения второй был в 2 раза больше, чем в первый раз. На сколько процентов каждый раз снижалась цена?

Решение: Для упрощения вычислений обозначим
X – первая скидка;
X/2 – вторая скидка.
Для вычисления неизвестной X составляем уравнение

Упрощаем, и сводим к квадратному уравнению

и решаем

Первый решение не имеет физического смысла, второй учитываем при вычислениях. Значение 0,2 соответствует снижению на 0,2*100%=20% после первой скидки, и X/2 =10% после второй скидки.

Задача 2. (557) Определенный товар стоил 200 грн. Сначала его цену повысили на несколько процентов, а затем снизили на столько же процентов, после чего стоимость его стала 192 грн. На сколько процентов каждый раз происходила смена цены товара?

Решение: Поскольку проценты одинаковы, то обозначаем изменении цены товара через X.
На основе условия задачи получим уравнение

Его упрощение приведет к решению уравнения

откуда корни приобретут значений

Первая значение отвергаем, оно меняет суть задачи (сначала имеем снижение, а затем рост процентов, противоречит условию). Второе при пересчете составит 0,2*100%=20% процентов.

Задача 3. (558) Вкладчик положил в банк 4000 грн. За первый год ему начислена определенный процент годовых, а второго года банковский процент увеличен на 4%. На конец второго года на счете стало 4664 грн. Сколько процентов составила банковская ставка в первый год?

Решение: Обозначим через X – увеличение вклада в первый год, тогда
X+4/100%=X+0,04
начисления во второй год.
По условию задачи составляем уравнение для определения неизвестной X

После упрощений получим квадратное уравнение вида

Вычисляем дискриминант

и корни уравнения

Первый корень отбрасываем, второй соответствует ставке в 6% годовых.

Задача 4. (564) В сосуде 12 кг кислоты. Часть кислоты отлили и долили до прежнего уровня водой. Затем снова отлили столько же, как и в первый раз, и долили водой до прежнего уровня. Сколько литров жидкости отливали каждый раз, если в результате получили 25-процентный раствор кислоты?

Решение: Обозначим через X – часть кислоты, которую отливали.
После первого раза ее осталось 12-X, а процентное содержание кислоты

После второй попытки содержание кислоты в сосуде составило
.
Разведя водой до 12 кг, процентное содержание составляло 25%. Составляем уравнение

Упрощаем проценты и избавляемся знаменателей

Решаем квадратное уравнение

Условии задачи удовлетворяет второе решение, а это значит, что каждый раз отливали 6 кг жидкости.

На этом знакомство со сложными процентами завершается. На практике Вам встретятся как простые так и сложные задачи. При проблемах с вычисления сложных процентов обращайтесь к нам, мы поможем Вам в решении задач.

Как определяется интерес? • арбитраж

В международном арбитраже, арбитры имеют широкую свободу действий при оценке убытков и присуждении процентов. Не существует единого подхода к определению процентной ставки, присуждаемой в арбитражных решениях.. Часто, арбитражные суды присуждают проценты, которые отражают позицию, в которой был бы истец, действие или бездействие ответчика никогда не имело места, или если причитающиеся суммы были выплачены своевременно. В другие времена, арбитры придерживаются совершенно другого подхода.

Проценты до и после вынесения решения в международном арбитраже

Проценты до вынесения решения часто предоставляются в арбитражных решениях. Целью предварительного вознаграждения является компенсация стороне, которая, на протяжении всего периода неуплаты, был лишен использования и распоряжения капиталом, который он должен был получить. Соответственно, арбитры часто начисляют проценты с даты выплаты, и к этой сумме начисляются проценты, пока не будет произведена полная оплата.

Проценты до присуждения могут составлять важную часть общей суммы убытков.. Например, в Тенарис С.А. и Тальта v. Венесуэла ICSID Дело №. ARB / 11/26, в то время как основной ущерб составил $ 87.3 миллиона, проценты до присуждения вознаграждения составили в долларах США 85.5 миллиона. Арбитражный суд решил, что проценты должны начисляться по усложненной ставке, рассчитанной на сумму убытков, понесенных заявителем в апреле. 2008 до последней награды в январе 2016. Таким образом, общая сумма компенсации составила $ США. 172,801,213.70.[1] В Марвин Фельдман v. Мексика ICSID Дело №. миллиард(О)/99/1, трибунал присудил 7.5 миллионов мексиканских песо в качестве процентов до выплаты вознаграждения, в то время как основной ущерб составил 9.5 миллион песо. Суд увеличил общую сумму компенсации на простые проценты, рассчитанные с даты, когда налоговые скидки должны были быть уплачены, до даты принятия решения.. Окончательная сумма, которую должен выплатить респондент, составила 16,961,056 Мексиканские песо.[2]

тем не менее, проценты до присуждения могут быть исключены в следующих случаях:

на упущенную будущую прибыль, если они не дисконтируются до даты, предшествующей награде;
если награда уже учитывает уровень инфляции. Большинство рыночных ставок, такие как LIBOR (который перестанет существовать 31 Декабрь 2021) и EURIBOR, включать темпы инфляции; или
если датой компенсации для целей оценки является дата самой компенсации. В ADC Affiliate Limited v. Венгрия ICSID Дело №. ARB / 03/16, например, арбитражный суд постановил, что «поскольку расчет основан на стоимости отчужденных инвестиций на дату присуждения, проценты до присуждения не начислялись».[3]

Проценты после присуждения, в очереди, aims to compensate a respondent’s avoidance in making an arbitral award’s payment in a timely manner. Отправной точкой для начисления процентов после присуждения может быть дата вынесения решения., или более поздняя дата. Например, арбитражный суд может разрешить ответчику произвести оплату в течение нескольких месяцев после вынесения решения, без процентов. В случае опозданий, начисление процентов после присуждения вознаграждения начинается с этой даты в будущем.

На практике, предварительно- и проценты после присуждения вознаграждения часто применяются по той же ставке. Альтернативно, проценты после присуждения могут быть выше как средство поощрения ответчика к возмещению присужденного ущерба, противодействие необходимости исполнительного производства. Например, если респонденту необходимо выплатить долг со значительной премией по умолчанию, процентная ставка после присуждения, которая ниже стоимости заимствования, такой как “без риска” ставка без спреда, вряд ли побудит респондента своевременно выплатить вознаграждение .

Простой и сложный процент

Арбитражные суды все чаще применяют стандарт полной компенсации в виде сложных процентов. Это так потому, что временная стоимость денег в странах со свободной рыночной экономикой измеряется в сложных процентах. (за исключением некоторых систем с шариат-основанные на законах). Часто считается, что простой процент не обеспечивает полного возмещения убытков заявителя..

Согласно многим национальным законам, арбитражные суды имеют право присуждать сложные проценты. Одним из примеров является Раздел 49(3) Закона об арбитраже Англии который прямо уполномочивает арбитражные суды «Присуждение простых или сложных процентов».

Некоторые арбитражные правила также уполномочивают арбитров назначать простые или сложные проценты. (видеть, например, Статья 31(4) Международного центра разрешения споров (ICDR) правила). В отличие от, положения Гражданского кодекса Германии о процентах запрещают сложный моральный процент (видеть Раздел 289 Гражданского кодекса Германии).

В инвестиционном арбитраже, данные свидетельствуют о том, что составные проценты предпочтительнее арбитражными судами при принятии решений примерно 2010 вперед. Одно исключение — случай, определенный в 2012 (SGS Societe Generale de Surveillance S.A. v. Парагвай, ICSID Дело №. ARB / 07/29), в котором сам истец «запрошенный простой процент на основе США. 30-дневная ставка LIBOR в долларах […] плюс два процентных пункта.»[4]

Процентные ставки, применяемые в арбитражных решениях

Если стороны прямо договорились о фиксированной процентной ставке или о методе расчета процентов, арбитры обычно применяют проценты в соответствии с соглашением сторон. Отправной точкой для арбитров обычно являются стороны’ соглашение, так как законодательством большинства стран предусмотрена выплата процентов по согласованию сторон’ соглашение. Стороны’ договор о процентах может заключаться на основе сторон’ первоначальный контракт, в соответствии с арбитражным регламентом, выбранным сторонами или через стороны’ представления в арбитраж.

При отсутствии такого соглашения, суды обладают широким дискреционным правом и могут назначать проценты на основе своего субъективного мнения о том, что необходимо для получения полной компенсации, на основании закона, применимого к спору, или даже, во время, на основании закона места арбитража. Значительное количество арбитров решили, что они могут определить “коммерчески разумный” процентная ставка.

Многие законы, например, швейцарский закон, разрешить требование о фактических убытках, превышающих допустимую установленную законом ставку. По немецкому законодательству, истец может также попытаться доказать свои фактические убытки на основании лишения его возможности использования капитала. С другой стороны, некоторые законы, например, египетский закон, разрешать требование о возмещении фактического ущерба сверх установленных законом интересов, только если должник действовал недобросовестно.

Многие арбитражные решения предусматривают процентные ставки, выраженные в плавающих контрольных показателях коммерческого заимствования., т.е.., обычно используемый коммерческий тариф. Общие ориентиры — LIBOR., EURIBOR, EONIA и US Prime. Эти контрольные показатели будут меняться в течение соответствующего периода и могут быть добавлены за счет спреда. (например, ставка LIBOR может быть добавлена 50 базисные точки, т.е.., ЛИБОР + 0.5%).

Коммерческие эталоны имеют разные сроки погашения. Например, шестимесячная ставка LIBOR отражает процентную ставку, которую несет банк по шестимесячной ссуде.. В этом случае, предполагается, что банк-кредитор уполномочен, через шесть месяцев, одолжить эти деньги, с начисленными процентами, другому заемщику. Когда ставка погашения выражена в годовом исчислении, банк-кредитор сможет использовать деньги только через двенадцать месяцев. При применении сложных процентов, чем короче период, тем быстрее будет расти начисленный процент. Вот почему годовой сложный процент отражает более «консервативный» подходить, на который часто ссылаются в арбитражных решениях. Например, в Неверие v. Коста Рика ICSID Дело №. ARB / 08/1, трибунал применил пятилетнюю ставку казначейства США. Суд счел, что процентная ставка должна быть консервативной., который сохраняет стоимость оценки, определенную трибуналом, и предполагает среднесрочные инвестиции с низким уровнем риска.[5]

Консервативный подход может быть выражен в «без риска» ставки, которые представляют собой стоимость ссуды для некоторых правительств (т.е.., доходность облигаций, выпущенных некоторыми правительствами, используется для измерения «без риска”Процентная ставка в конкретной стране). Эти ставки общедоступны и, в теории, устанавливается в соответствии с рыночными условиями каждой страны (например, то Эффективная ставка федерального фонда В Соединенных Штатах). Эти ставки также имеют разные сроки погашения и, следовательно, разные урожаи, поэтому арбитры должны указать, на какой срок они ссылаются. Например, В Соединенных Штатах, государственные ценные бумаги, срок погашения которых составляет менее одного года, называются казначейскими векселями. (“Казначейские векселя”), тогда как государственные ценные бумаги со сроком погашения более одного года известны как казначейские облигации или векселя..

В некоторых случаях, суды могут применять фиксированные ставки, вместо плавающих рыночных ставок, на основании того, что они считают разумным и справедливым для выплаты компенсации истцу. В контексте инвестиционного арбитража, использовались фиксированные ставки, исходя из рисков, связанных с инвестированием в конкретное государство. Например, в Alpha Project Holding в Украине ICSID Дело №. ARB / 07/16, проценты были присуждены в 9.1%, ежегодно в течение пяти лет. По мнению арбитражного суда, «эта ставка лучше отражает альтернативные издержки связанных с потерями Заявителя, с поправкой на риски инвестирования на Украине».[6] таким образом, фиксированная ставка может быть намеренно выше, чтобы отразить неопределенность, которую истец понес бы с рискованными инвестициями.

в заключение, разные валюты, естественно, имеют разные процентные ставки. Идеально, используемый курс будет соответствовать валюте арбитражного решения. Один арбитражный суд заметил, что это «в корне неверно в принципе, применять любую процентную ставку, полученную из одной валюты, к совершенно другой валюте».[7]

[1] Тенарис С.А. и Talta — Торговая и маркетинговая компания Sociedade Unipessoal Lda. v. Боливарианская Республика Венесуэла ICSID Дело №. ARB / 11/26, Награда от 29 январь 2016, для. 594.

[2] Марвин Рой Фельдман v. Мексиканские Соединенные Штаты, ICSID Дело №. миллиард(О)/99/1, Награда от 16 Декабрь 2002, для. 205.

[3] ADC Affiliate Limited и ADC & ADMC Management Limited v. Венгерская Республика, ICSID Дело №. ARB / 03/16, Решение Трибунала от 2 октября 2006, для. 520.

[4] SGS Societe Generale de Surveillance S.A. v. Республика Парагвай, ICSID Дело №. ARB / 07/29, Награда от 6 февраль 2012, для. 186.

[5] Марион Неверие v. Республика Коста-Рика, ICSID Дело №. ARB / 08/1, Награда от 16 май 2012, лучший. 319, 324.

[6] Alpha Projektholding GmbH v. Украина, ICSID Дело №. ARB / 07/16, Награда от 8 ноябрь 2008, для. 514.

[7] Gemplus SA & Орс — Мексиканские Соединенные Штаты & Талсуд С.А. — Мексиканские Соединенные Штаты, ICSID Дело №. миллиард(О)/04/3, Награда от 16 июнь 2010, для. 16-32.

Узнайте о простых и сложных процентах

Проценты определяются как стоимость заимствования денег, как в случае процентов, начисляемых на остаток кредита. И наоборот, проценты также могут быть ставкой, выплачиваемой за деньги на депозите, как в случае депозитного сертификата. Проценты можно рассчитывать двумя способами: простой процент или сложный процент.

Простые проценты начисляются на основную или первоначальную сумму ссуды.
Сложные проценты рассчитываются на основе основной суммы, а также накопленных процентов за предыдущие периоды, и, таким образом, могут рассматриваться как «проценты на проценты». «

Сумма процентов, подлежащих уплате по ссуде, может сильно отличаться, если проценты рассчитываются на сложной, а не простой основе. С положительной стороны, магия начисления сложных процентов может работать вам на пользу, когда дело касается ваших инвестиций, и может стать мощным фактором создания богатства.

Хотя простые проценты и сложные проценты являются основными финансовыми концепциями, тщательное знакомство с ними может помочь вам принимать более обоснованные решения при получении ссуды или инвестировании.

Формула простого процента

Формула расчета простых процентов:

Простой процент = P × i × n, где: P = Основная сумма = Ставка процента = Срок ссуды \ begin {align} & \ text {Simple Interest} = P \ times i \ times n \\ & \ textbf {где:} \\ & P = \ text {Принципал} \\ & i = \ text {Процентная ставка} \\ & n = \ text {Срок кредита} \\\ end {выровнен} Простой процент = P × i × n, где: P = Основная сумма = Ставка процента = Срок кредита

Таким образом, если простые проценты взимаются в размере 5% по ссуде в размере 10 000 долларов, взятой на три года, общая сумма процентов, подлежащих уплате заемщиком, рассчитывается как 10 000 долларов x 0. n — 1 \ big) \\ & \ textbf {где:} \\ & P = \ text {Принципал} \\ & i = \ text {Процентная ставка в процентах} \\ & n = \ text {Количество периодов начисления сложных процентов за год} \ \ \ end {align} Сложный процент = (P (1 + i) n) −PCСложный процент = P ((1 + i) n − 1), где: P = Основная сумма = Процентная ставка в процентах n = Количество периодов начисления сложных процентов на год

Сложные проценты = Общая сумма основной суммы долга и процентов в будущем (или будущей стоимости) за вычетом суммы основного долга в настоящее время, называемой приведенной стоимостью (PV).3 — 1 \ big) \\ & = \ 10 000 $ \ big (1.157625 — 1 \ big) \\ & = \ 1576,25 $ \\ \ end {выровнено} Процентная ставка = 10 000 долларов США ((1 + 0,05) 3−1) = 10 000 долларов США (1,157625−1) = 1 576,25 долл. США

Хотя общая сумма процентов, подлежащих выплате в течение трехлетнего периода по этому займу, составляет 1 576,25 долларов США, в отличие от простых процентов, сумма процентов не одинакова для всех трех лет, поскольку сложные проценты также учитывают накопленные проценты за предыдущие периоды.

Проценты, подлежащие выплате в конце каждого года, показаны в таблице ниже.

Год	Начальное сальдо (P)	Процентная ставка 5% (I)	Конечное сальдо (P + I)
1	10 000,00 долларов США	500,00 долл. США	10 500,00 долларов США
2	10 500,00 долларов США	525,00 $	$ 11 025,00
3	11 025 долларов.00	$ 551,25	11 576,25 долл. США
Итого проценты		$ 1 576,25

Периоды начисления

При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение. Как правило, чем выше количество периодов начисления сложных процентов, тем больше сумма сложных процентов. Таким образом, на каждые 100 долларов кредита в течение определенного периода сумма процентов, начисленных по ставке 10% годовых, будет ниже, чем процентная ставка, начисляемая по ставке 5% раз в полгода, что, в свою очередь, будет ниже, чем процент, начисляемый по ставке 2.5% ежеквартально.

В формуле для расчета сложных процентов переменные «i» и «n» должны быть скорректированы, если количество периодов начисления сложных процентов составляет более одного раза в год.

То есть в круглых скобках «i» или процентная ставка должна быть разделена на «n» — количество периодов начисления сложных процентов в году. За пределами круглых скобок «n» необходимо умножить на «t», то есть общую длину инвестиции.

Следовательно, для 10-летнего кредита под 10%, когда проценты начисляются каждые полгода (количество периодов начисления сложных процентов = 2), i = 5% (т. {nt} — 1 \ Big) \\ & \ textbf {где:} \\ & P = \ text {Principal} \\ & i = \ text {Процентная ставка в процентах} \\ & n = \ text {Количество периодов начисления сложных процентов в год} \\ & t = \ text {Общее количество лет для инвестиции или ссуды} \\ \ end {выровнено} Общая стоимость со сложным процентом = (P (n1 + i) nt) −PCompound Interest = P ( (n1 + i) nt − 1) где: P = основная сумма i = процентная ставка в процентах n = количество периодов начисления сложных процентов в год = общее количество лет для инвестиции или кредита

Следующая таблица демонстрирует разницу в том, что количество периодов начисления сложных процентов может составлять сверхурочные для ссуды в размере 10 000 долларов, взятой на 10-летний период.

Частота смешивания	Количество периодов начисления процентов	Значения для i / n и nt	Итого проценты
Ежегодно	1	i / n = 10%, nt = 10	$ 15 937,42
Раз в полгода	2	i / n = 5%, nt = 20	$ 16 532,98
Ежеквартально	4	i / n = 2,5%, nt = 40	16850 долларов США. 64
Ежемесячно	12	i / n = 0,833%, nt = 120	17059,68 долл. США

Другие концепции начисления сложных процентов

Временная стоимость денег

Поскольку деньги не являются «бесплатными», но имеют стоимость в виде процентов, из этого следует, что доллар сегодня будет стоить больше, чем доллар в будущем. Эта концепция известна как временная стоимость денег и является основой для относительно продвинутых методов, таких как анализ дисконтированных денежных потоков (DCF).Противоположность начислению сложных процентов называется дисконтированием. Фактор дисконтирования можно рассматривать как обратную величину процентной ставки и коэффициент, на который необходимо умножить будущую стоимость, чтобы получить текущую стоимость.

Формулы для получения будущей стоимости (FV) и текущей стоимости (PV) следующие:

FV = PV × (1 + in) ntPV = FV ÷ (1 + in) nt где: i = процентная ставка в процентах n = количество периодов начисления сложных процентов в год = общее количество лет для инвестиции или кредита \ begin {выровнено} & \ text {FV} = PV \ times \ big (\ frac {1 + i} {n} \ big) ^ {nt} \\ & \ text {PV} = FV \ div \ big (\ frac {1 + i} {n} \ big) ^ {nt} \\ & \ textbf {где:} \\ & i = \ text {Процентная ставка в процентах} \\ & n = \ text {Количество периодов начисления сложных процентов в год} \\ & t = \ text {Общее количество лет для инвестиции или кредита} \\ \ end {выровнено} FV = PV × (n1 + i) ntPV = FV ÷ (n1 + i) nt, где: i = процентная ставка в процентные условия n = количество периодов начисления сложных процентов в год = общее количество лет для инвестиций или ссуды

Например, будущая стоимость 10 000 долларов США составит 5% годовых в течение трех лет:

= 10 000 долларов США (1 + 0. 05) ³

= 10 000 долл. США (1 157 625 долл. США)

= 11 576,25 долларов США.

Приведенная стоимость 11 576,25 долларов США со скидкой 5% на три года:

= 11 576,25 долл. США / (1 + 0,05) ³

= 11 576,25 долл. США / 1 157 625 долл. США

= 10 000 долларов США

Обратное значение 1,157625, равное 0,8638376, в данном случае является коэффициентом дисконтирования.

Правило 72

Правило 72 рассчитывает приблизительное время, в течение которого инвестиция удвоится при заданной норме прибыли или процентах «i» и определяется выражением (72 / i).Его можно использовать только для годового начисления сложных процентов, но он может быть очень полезен при планировании того, сколько денег вы можете рассчитывать получить на пенсии.

Например, инвестиция с годовой доходностью 6% удвоится через 12 лет (72/6%).

Инвестиции с годовой доходностью 8% вырастут вдвое за девять лет (72/8%).

Совокупный годовой темп роста (CAGR)

Совокупный годовой темп роста (CAGR) используется для большинства финансовых приложений, которые требуют расчета единого темпа роста за период.

Например, если ваш инвестиционный портфель вырос с 10 000 до 16 000 долларов за пять лет, каков CAGR? По сути, это означает, что PV = 10 000 долларов США, FV = 16 000 долларов США, nt = 5, поэтому необходимо вычислить переменную «i». Используя финансовый калькулятор или электронную таблицу Excel, можно показать, что i = 9,86%.

Обратите внимание, что в соответствии с соглашением о движении денежных средств ваши первоначальные инвестиции (PV) в размере 10 000 долларов США отображаются со знаком минус, поскольку они представляют собой отток средств. Чтобы найти «i» в приведенном выше уравнении, PV и FV обязательно должны иметь противоположные знаки.

Реальные приложения

CAGR широко используется для расчета доходности за периоды для акций, паевых инвестиционных фондов и инвестиционных портфелей. CAGR также используется для определения того, превышал ли управляющий паевым инвестиционным фондом или управляющий портфелем рыночную норму прибыли за период. Например, если рыночный индекс обеспечил общую доходность 10% за пять лет, но управляющий фондом получил только 9% годовой прибыли за тот же период, это означает, что управляющий отстал от рынка.

CAGR также можно использовать для расчета ожидаемых темпов роста инвестиционных портфелей в течение длительных периодов, что полезно для таких целей, как накопление на пенсию. Рассмотрим следующие примеры:

Не склонный к риску инвестор доволен скромной годовой доходностью 3% по своему портфелю. Таким образом, ее нынешний портфель в 100 000 долларов вырастет до 180 611 долларов через 20 лет. Напротив, толерантный к риску инвестор, ожидающий годовой доходности своего портфеля в размере 6%, через 20 лет увидит, что 100 000 долларов вырастут до 320 714 долларов.
CAGR можно использовать для оценки того, сколько нужно убрать, чтобы сэкономить для конкретной цели. Пара, которая хотела бы сэкономить 50 000 долларов в течение 10 лет на первоначальный взнос за кондоминиум, должна будет экономить 4 165 долларов в год, если они предполагают, что годовой доход (CAGR) составит 4% от своих сбережений. Если они готовы взять на себя дополнительный риск и ожидать среднегодового роста в 5%, им нужно будет ежегодно экономить 3975 долларов.
CAGR также можно использовать для демонстрации достоинств инвестирования раньше, чем позже.Если цель состоит в том, чтобы сэкономить 1 миллион долларов к выходу на пенсию в возрасте 65 лет, исходя из среднегодового роста в 6%, 25-летнему человеку для достижения этой цели потребуется откладывать 6 462 доллара в год. С другой стороны, 40-летнему человеку нужно будет сэкономить 18 227 долларов, что почти в три раза больше, чтобы достичь той же цели.

Дополнительные соображения по интересам

Убедитесь, что вы знаете точную годовую ставку платежа (APR) по вашему кредиту, поскольку метод расчета и количество периодов начисления сложных процентов могут повлиять на ваши ежемесячные платежи. Хотя банки и финансовые учреждения имеют стандартизированные методы расчета процентов, подлежащих уплате по ипотеке и другим займам, расчеты могут незначительно отличаться от страны к стране.

Компаундирование может работать в вашу пользу, когда дело касается ваших инвестиций, но оно также может работать на вас при выплате кредита. Например, если выплачивать половину ипотечного платежа дважды в месяц вместо того, чтобы вносить полную выплату один раз в месяц, в конечном итоге вы сократите срок погашения и сэкономите значительную сумму процентов.

Компаундирование может работать против вас, если у вас есть ссуды с очень высокими процентными ставками, например, по кредитной карте или долгам универмага. Например, остаток на кредитной карте в размере 25 000 долларов США с процентной ставкой 20% (сложенный ежемесячно) приведет к общей сумме процентов в размере 5 485 долларов США за год или 457 долларов США в месяц.

Итог

Получите магию сложного вознаграждения, работающего на вас, регулярно инвестируя и увеличивая частоту погашения кредита. Ознакомление с основными понятиями простых и сложных процентов поможет вам принимать более обоснованные финансовые решения, сэкономив тысячи долларов и со временем увеличив свой собственный капитал.

Сравнить счета

Раскрытие информации рекламодателя

Предложения, представленные в этой таблице, поступают от партнерств, от которых Investopedia получает компенсацию.

Страница не найдена

Образование
- Общий
  - Словарь
  - Экономика
  - Корпоративные финансы
  - Рот ИРА
  - Акции
  - Паевые инвестиционные фонды
  - ETFs
  - 401 (к)
- Инвестирование / Торговля
  - Основы инвестирования
  - Фундаментальный анализ
  - Управление портфелем
  - Основы трейдинга
  - Технический анализ
  - Управление рисками
Рынки
- Новости
  - Новости компании
  - Новости рынков
  - Торговые новости
  - Политические новости
  - Тенденции
- Популярные акции
  - Яблоко (AAPL)
  - Тесла (TSLA)
  - Amazon (AMZN)
  - AMD (AMD)
  - Facebook (FB)
  - Netflix (NFLX)
Симулятор
- Симулятор
  - Завести аккаунт
  - Присоединиться к игре
- Мой симулятор
  - Моя игра
  - Создать игру
Твои деньги
- Личные финансы
  - Управление капиталом
  - Бюджетирование / экономия
  - Банковское дело
  - Кредитные карты
  - Домовладение
  - Пенсионное планирование
  - Налоги
  - Страхование
- Обзоры и рейтинги
  - Лучшие онлайн-брокеры
  - Лучшие сберегательные счета
  - Лучшие домашние гарантии
  - Лучшие кредитные карты
  - Лучшие личные займы
  - Лучшие студенческие ссуды
  - Лучшее страхование жизни
  - Лучшее автострахование
Советники
- Ваша практика
  - Управление практикой
  - Продолжая образование
  - Карьера финансового консультанта
  - Инвестопедия 100
- Управление капиталом
  - Портфолио Строительство
  - Финансовое планирование
Академия
- Популярные курсы
  - Инвестирование для начинающих
  - Станьте дневным трейдером
  - Торговля для начинающих
  - Технический анализ
- Курсы по темам
  - Все курсы
  - Торговые курсы
  - Курсы инвестирования
  - Финансовые профессиональные курсы

Представлять на рассмотрение

Извините, страница, которую вы ищете, недоступна.

Вы можете найти то, что ищете, используя наше меню или параметры поиска. дома

О нас
Условия эксплуатации
Словарь
Редакционная политика
Рекламировать
Новости
Политика конфиденциальности
Связаться с нами
Карьера
Уведомление о конфиденциальности Калифорнии

#
А
B
C
D
E
F
грамм
ЧАС
я
J
K
L
letter-m»> M
N
О
п
Q
р
S
Т
U
V
W
Икс
Y
Z

Investopedia является частью издательской семьи Dotdash.

Страница не найдена

Образование
- Общий
  - Словарь
  - Экономика
  - Корпоративные финансы
  - Рот ИРА
  - Акции
  - Паевые инвестиционные фонды
  - ETFs
  - 401 (к)
- Инвестирование / Торговля
  - Основы инвестирования
  - Фундаментальный анализ
  - Управление портфелем
  - Основы трейдинга
  - Технический анализ
  - Управление рисками
Рынки
- Новости
  - Новости компании
  - Новости рынков
  - Торговые новости
  - Политические новости
  - Тенденции
- Популярные акции
  - Яблоко (AAPL)
  - Тесла (TSLA)
  - Amazon (AMZN)
  - AMD (AMD)
  - Facebook (FB)
  - Netflix (NFLX)
Симулятор
- Симулятор
  - Завести аккаунт
  - Присоединиться к игре
- Мой симулятор
  - Моя игра
  - Создать игру
Твои деньги
- Личные финансы
  - Управление капиталом
  - Бюджетирование / экономия
  - Банковское дело
  - Кредитные карты
  - Домовладение
  - Пенсионное планирование
  - Налоги
  - Страхование
- Обзоры и рейтинги
  - Лучшие онлайн-брокеры
  - Лучшие сберегательные счета
  - Лучшие домашние гарантии
  - Лучшие кредитные карты
  - Лучшие личные займы
  - Лучшие студенческие ссуды
  - Лучшее страхование жизни
  - Лучшее автострахование
Советники
- Ваша практика
  - Управление практикой
  - Продолжая образование
  - Карьера финансового консультанта
  - Инвестопедия 100
- Управление капиталом
  - Портфолио Строительство
  - Финансовое планирование
Академия
- Популярные курсы
  - Инвестирование для начинающих
  - Станьте дневным трейдером
  - Торговля для начинающих
  - Технический анализ
- Курсы по темам
  - Все курсы
  - Торговые курсы
  - Курсы инвестирования
  - Финансовые профессиональные курсы

Представлять на рассмотрение

Извините, страница, которую вы ищете, недоступна.

Вы можете найти то, что ищете, используя наше меню или параметры поиска. дома

О нас
Условия эксплуатации
Словарь
Редакционная политика
Рекламировать
Новости
Политика конфиденциальности
Связаться с нами
Карьера
Уведомление о конфиденциальности Калифорнии

#
А
B
C
D
E
F
грамм
ЧАС
я
J
K
L
letter-m»> M
N
О
п
Q
р
S
Т
U
V
W
Икс
Y
Z

Investopedia является частью издательской семьи Dotdash.

Наглядное руководство по простым, сложным и непрерывным процентным ставкам — лучше объяснение

Процентные ставки сбивают с толку, несмотря на их повсеместное распространение. В этом посте подробно рассматривается, почему процентные ставки ведут себя именно так.

Понимание этих концепций поможет понять финансы (ипотечные ставки и нормы сбережений), а также вездесущий e и натуральный логарифм. Вот наша шпаргалка:

Срок	Формула	Описание и использование
Простой		Фиксированная невозрастающая доходность (купоны по облигациям)
Соединение (Годовое)		Ежегодные изменения (фондовый рынок, инфляция)
Соединение (n раз в год)		Изменения каждый месяц / неделю / день (сберегательный счет)
Непрерывный рост		Меняется каждое мгновение (радиоактивный распад, температура)
APR	Годовая процентная ставка (без начисления сложных процентов)
APY	Годовая процентная доходность (включая все совокупные эффекты)

P = основная сумма, ваши первоначальные инвестиции (т.е.е., \ 1000 $)
r = процентная ставка (т. е. 5% годовых)
n = количество периодов времени (т. Е. 3 года)

И быстрый калькулятор для преобразования APR в APY:

К чему суета?

Процентные ставки сложны. Подобно римским цифрам и иероглифам, наша первая система «работала», но не была идеальной.

Вначале у вас могло быть 100 золотых монет, и вам платили 12% в год (процент = процент = за сотню — эти римские цифры все еще появляются!).Это достаточно просто: мы получаем 12 монет в год. Но действительно ли это 12?

Если мы разберем его, кажется, что мы зарабатываем 1 золото в месяц: 6 за январь-июнь и 6 за июль-декабрь. Но постойте — после выплаты в июне у нас будет 106 золотых в июле, а в остальное время мы заработаем только 6? Вы говорите, что 100 и 106 заработают одинаковую сумму за 6 месяцев? По этой логике, 100 и 200 тоже зарабатывают одинаковую сумму? Ой ой.

Эта проблема, казалось, не волновала древних египтян, но в 1600-х годах вызвала вопросы и привела к открытию Бернулли е (извините, любители математики, е не было обнаружено из-за некоторой догадки, что странный предел может иметь полезные свойства). Об этой загадке можно многое сказать — просто помните об этом, когда мы анализируем процентные ставки:

Процентные ставки и терминология были изобретены до идеи начисления сложных процентов. Черт возьми, ссуды были примерно в 1500 г. до н.э., до показателя степени, 0 или даже до десятичной точки! Поэтому неудивительно, что наши обсуждения могут запутаться.
Природа не ждет человеческий год перед изменением . Процентные доходы — это своего рода «рост», но такие природные явления, как температура и радиоактивный распад, меняются постоянно, каждую секунду и быстрее.n $ »: Природа грубо игнорирует наш календарь при внесении изменений.

Изучите Lingo

В результате этих осложнений нам нужно несколько терминов, чтобы обсудить процентные ставки:

APR (годовая процентная ставка): Ставка, которую вам говорят («12% в год!»). Вы увидите в формуле букву «r».
APY (годовая процентная доходность): Ставка, которую вы фактически получаете через год после учета всех начислений. Вы можете учитывать эту «общую прибыль» в формуле.APY больше или равен APR.

APR — это то, что вам сообщает банк, APY — это то, что вы платите (цена после налогов, доставки и обработки, если вы меня поняли). И, конечно же, банки рекламируют курс, который выглядит лучше.

Получите кредитную карту или автокредит? Они покажут вам «низкий APR», который вы платите, чтобы скрыть более высокий APY. Но открыть сберегательный счет? Ну, конечно, они рекламировали «высокую APY», которую платят за то, чтобы выглядеть щедро.

APY (фактическая доходность) — это то, что вас волнует, и способ сравнения конкурирующих предложений .

Простые проценты

Начнем с первого этажа: Простые проценты выплачивают фиксированную сумму с течением времени . Несколько примеров:

Басня Эзопа о золотом гуся: каждый день он нес одно золотое яйцо. Он не мог откладывать быстрее, и яйца не превращались в собственных золотых гусей.
Корпоративные облигации: Облигация с номинальной стоимостью 1000 долларов США и 5% процентной ставкой (купоном) приносит вам 50 долларов США в год до истечения срока ее действия. Вы не можете увеличить номинальную стоимость, поэтому вы получите 50 долларов в год по облигации.(На самом деле, облигация будет выплачиваться каждые 6 месяцев по $ 25).

Простые проценты — самый высокий Базовый вид доходности . Внесение $ 100 на счет с 50% простой (годовой) процентной ставкой выглядит так:

Вы начинаете с основной суммы (иначе говоря, инвестиций) в 100 долларов и зарабатываете 50 долларов каждый год. Я представляю синего директора, который каждый год «выгребает» зеленые деньги вверх.

Однако эти новые зеленые деньги не растут — они не могут расти! Из простого интереса, $ 50 просто сидит там.Только исходные 100 долларов могут «работать» по зарабатыванию денег.

Простой процент имеет простую формулу: каждый период вы зарабатываете P * r (основная сумма * процентная ставка). Через n периодов у вас будет:

Эта формула работает, пока «r» и «n» относятся к одному и тому же периоду времени. Это могут быть годы, месяцы или дни — хотя в большинстве случаев мы рассматриваем годовой процент. Здесь нет обмана, потому что здесь нет сложных процентов — проценты не могут расти.

Простой процент полезен, когда:

Ваши процентные доходы создают нечто, что не может расти больше .Это как золотой гусь, создающий яйца, или корпоративные облигации, выплачивающие деньги, которые нельзя реинвестировать.
Вам нужны простые, предсказуемые, неэкспоненциальные результаты . Предположим, вы поощряете своих детей делать сбережения. Вы можете объяснить, что будете откладывать 1 доллар в месяц в виде «забавных денег» на каждые 20 долларов в их копилке. Большинство детей будут в восторге и будут покупать комиксы каждый месяц. Если ваша фамилия Гринспен, ваш ребенок может попросить реинвестировать дивиденды.

На практике простые проценты встречаются довольно редко, поскольку большинство видов доходов можно реинвестировать.На самом деле нет различия между APR и APY, поскольку ваш доход не может измениться: вы всегда зарабатываете одну и ту же сумму в год.

Действительно понимание роста

На этом и заканчиваются самые интересные объяснения: вот формула, а теперь иди по своему пути. Не здесь: давайте посмотрим, что происходит на самом деле.

Во-первых, что означает процентная ставка? Я думаю об этом как о разновидности «скорости» :

50 миль / ч означает, что вы преодолеете 50 миль за час
r = 50% в год означает, что вы будете зарабатывать 50% от своей основной суммы в течение года.Если P = \ $ 100, вы будете зарабатывать \ $ 50 в год (ваша «скорость роста денег»).

Но у обоих типов скорости есть тонкость: нам не нужно ждать весь период времени!

Означает ли вождение 50 миль в час, что вы должны ехать целый час? Ни за что! Вы можете проехать «всего» 30 минут и проехать 25 миль (50 миль в час * 0,5 часа).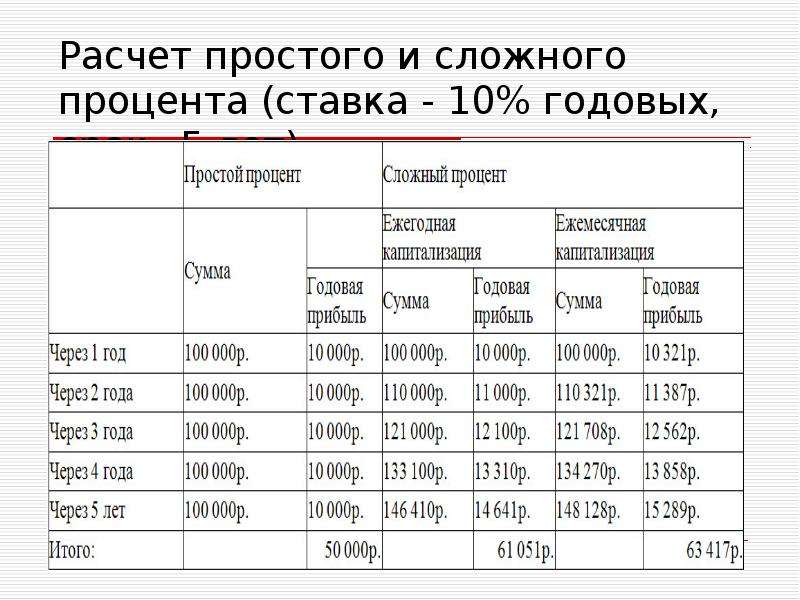 Вы можете проехать 15 минут и проехать 12,5 миль (50 миль в час * 0,25 часа). Вы уловили идею.

Процентные ставки аналогичны. Процентная ставка дает вам «траекторию» или «темп», по которым нужно следовать.Если у вас есть \ $ 100 при простой процентной ставке 50%, ваш темп составит \ $ 50 / год. Но вам не обязательно следовать в этом темпе целый год! Если вы росли 6 месяцев, вы должны иметь право на 25 долларов. Взгляните на это:

Начинаем с \ $ 100 синим цветом. Каждый год этот синий цвет приносит \ $ 50 (отмечен зеленым) в нашу общую сумму. Конечно, при простом проценте наши доходы основаны на нашей первоначальной сумме, а не на «новой сумме». Соединение точек дает нам линию тренда: мы идем по пути $ 50 в год.Наши выплаты выглядят как лестница, потому что нам платят только в конце года, но траектория все еще работает.

Простой процент сохраняет ту же траекторию: мы зарабатываем «P * r» каждый год, независимо от того, сколько (\ $ 50 / год в данном случае). Эта прямая идеально предсказывает, где мы закончим.

Идея «следования по траектории» может показаться странной, но придерживайтесь ее — она действительно поможет в понимании природы e.

Один момент: траектория — это «насколько быстро» растет банковский счет в определенный момент.Из простого интереса мы застряли в машине, едущей с той же скоростью: \ 50 долларов в год или 50 миль в час. В других случаях наша скорость может измениться, как у парашютиста: они начинают медленно, но с каждой секундой падают все быстрее и быстрее. Но в в любой момент есть одна скорость, одна траектория.

(Гуру математики назовут эту траекторию «производной» или «градиентом». Пока не нужно бить москита кувалдой для исчисления.)

Базовый сложный процент

Простой интерес должен заставить вас поежиться. Почему наши проценты не могут приносить деньги? Мы должны использовать выплаты по облигациям (\ $ 50 / год), чтобы покупать больше облигаций. Черт возьми, мы должны использовать золотые яйца для финансирования исследований по клонированию золотых гусей!

Сложный рост означает, что ваши проценты приносят проценты . Эйнштейн назвал это «одной из самых могущественных сил в природе», и это правда. Когда у вас есть растущая вещь, которая создает больше растущих вещей, которая создает больше растущих вещей … ваша прибыль быстро увеличивается.

Самый простой тип — это доходность за период, что обычно означает «год за годом».Реинвестирование нашей доли ежегодно выглядит так:

Мы зарабатываем $ 50 с 0 по 1 год, как с простым процентом. Но в год 1-2, теперь, когда наша общая сумма составляет 150 долларов, мы можем заработать 75 долларов в этом году (50% * 150), что даст нам 225 долларов. На 2-3 год у нас будет 225 долларов, так что мы зарабатываем 50% от этой суммы, или 112,50 долларов.

В целом, у нас в (1 + r) раз больше «вещей» каждый год. Через n лет это становится:

Экспоненциальный рост опережает простой линейный процент, который в 3-м году составлял всего $ 250 (100 + 3 * 50). 10 = 1,344 доллара, или на 34,4% больше за это десятилетие.

Интерес как завод

Типичная интерпретация рассматривает деньги как «каплю», которая со временем растет. Этот взгляд работает, но иногда мне нравится рассматривать процентные доходы как «фабрику», которая приносит больше денег:

Вот что происходит:

Год 0: Начнем с \ $ 100.
Год 1: Наши 100 долларов создают «облигацию» на 50 долларов.
Год 2: На 100 долларов создается еще одна облигация на 50 долларов.50 долларов создают облигацию на 25 долларов. Итого 50 + 25 = 75, что совпадает.
Год 3: Все становится немного сумасшедшим. \ $ 100 создает третью облигацию \ $ 50. Две существующие облигации по $ 50 составляют по $ 25 каждая. А 25 долларов составляют 12,50.
От 4 до бесконечности: Оставлено в качестве упражнения для читателя. (Тебе не нравится этот учебник?)

Это интересная точка зрения. \ $ 100 просто бездумно заводит \ $ 50 «фабрики», которые начинают зарабатывать деньги самостоятельно (обратите внимание на 3 синие стрелки от синей основной к зеленой \ 50 $).Эти фабрики за $ 50 создают фабрики за $ 25 и так далее.

Схема кажется сложной, но в некотором смысле она проще. Те \ 100 не знают, что делают эти сумасшедшие \ $ 50: насколько известно \ 100 $, мы зарабатываем только \ $ 50 в год.

Так чем же полезна эта точка зрения?

Вы можете отделить влияние родителя (\ $ 100) от детей. Например, в 3-м году у нас всего $ 337,50. Родитель заработал \ $ 150 («3 * 50% * \ $ 100 = \ $ 150», используя простую формулу процентов!).Это означает, что различные «дети» внесли \ $ 337,50 — \ 150 $ — \ 100 = \ 87,50 $, или около 1/3 общей суммы.
Разбивка доходов на компоненты помогает понять e. Больше узнать об e — это хорошо, потому что он появляется везде.

Кроме того, всегда весело видеть старые идеи в новом свете.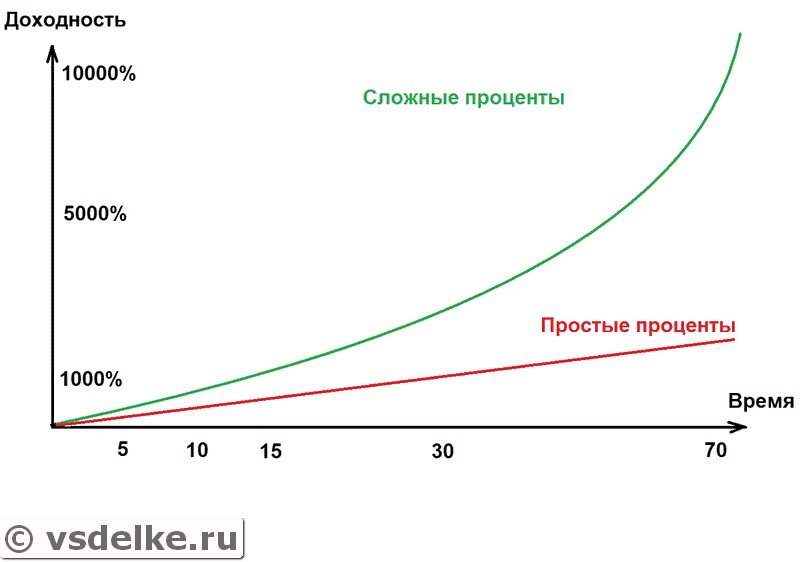 По крайней мере, для одного из нас.

Понимание траектории

О, мы еще не закончили. Еще одно наблюдение — взгляните на нашу траекторию:

Из простого интереса мы всегда держали тот же темп (\ $ 50 / год — довольно скучно).С ежегодно начисленными процентами мы получаем новую траекторию каждый год.

Вкладываем деньги, ложимся спать и просыпаемся в конце года:

Год 1: «Эй, подожди. У меня 150 долларов! Я должен зарабатывать 75 долларов в год, а не 50 долларов! ». Вы кричите на своего банкира, поднимаете ручку до 75 долларов в год и снова ложитесь спать.
Год 2: «Эй! У меня 225 долларов, а я должен зарабатывать 112,50 долларов в год! ». Вы кричите в свой банк, и вам нужно изменить курс.

Этот процесс повторяется вечно — кажется, мы никогда не учимся.

Повторное рассмотрение сложных процентов

Почему мы так долго ждем? Конечно, лучше ждать год за раз, чем ждать «вечно» (например, простой процент), но я думаю, что мы можем добиться большего. Увеличим год:

Посмотрите, что происходит. Зеленая линия представляет наш начальный темп (\ $ 50 / год), а сплошная область показывает денежные средства на нашем счете. Через 6 месяцев мы заработали 25 долларов, но не видим ни цента! Что еще более важно, через 6 месяцев у нас будет та же траектория, что и в начале.Процентный разрыв показывает, где мы заработали проценты, но остаемся на нашей первоначальной траектории (основанной на первоначальной основной сумме). Мы теряем то, что должны делать.

Представьте, я взял ваши деньги и вернул их через 6 месяцев. «Ну, понимаете, я не пользовался им целый год, так что я не должен вам никакого интереса. Ведь проценты измеряются по годам. Per yeeeeeaaaaar. Не за 6 месяцев ». Ты бы улыбнулся и отправил Буббу сломать мне ноги.

Ежегодные выплаты — это искусственные артефакты, используемые для простоты.Но на самом деле деньги нужно зарабатывать постоянно. Мы можем выплатить проценты через 6 месяцев, чтобы сократить разрыв:

Вот что произошло:

Начнем с \ $ 100 и траектории \ $ 50 / год, как обычно
Через 6 месяцев мы получаем 25 долларов, что дает нам 125 долларов
Выходим по новой траектории: 50% * \ 125 $ = \ 62,5 $ / год
Через 6 месяцев мы собираем 62,5 / год, умноженные на 0,5 года = 31,25. У нас 125 + 31,25 = 156,25.

Ключевым моментом является то, что наша траектория улучшилась на полпути, и мы заработали 156.2 $. Если повторить это в течение t лет (умножить на t раз), получим:

Сложные проценты сокращают «мертвую зону», в которой наши проценты не приносят процентов . Чем чаще мы складываем, тем меньше разрыв между получением процентов и обновлением траектории.

Непрерывный рост

Ясно, что мы хотим, чтобы деньги «приходили в онлайн» как можно быстрее. Непрерывный рост — это сложные проценты на стероиды: вы сокращаете разрыв до небытия, разделяя год на все больше и больше периодов времени:

Чистый эффект заключается в использовании процентов сразу после их создания.Ждем миллисекунду, находим новую сумму и отправляемся по новой траектории. За исключением того, что это не каждая миллисекунда: это каждая наносекунда, пикосекунда, фемтосекунда и интервалы, названия которых я не знаю. Постоянный рост позволяет идеально синхронизировать траекторию с вашей текущей суммой. (.365 $ достаточно для вашего банковского счета, большое вам спасибо. А если серьезно, то ежедневное начисление сложных процентов является хорошим приближением к непрерывному росту.)

Экспонента e — это мост от нашего скачкообразного «замедленного» роста к плавным изменениям в мире природы.

Несколько примеров

Давайте попробуем несколько примеров, чтобы убедиться, что они окупаются. Помните: APR — это ставка, которую они вам дают, APY — это то, что вы фактически зарабатываете (ваша истинная доходность).

Это 4.4 = 4,47% $, поэтому 4,5% годовых все же лучше.
Должен ли я платить по ипотеке в конце месяца или в начале? Начало, конечно. Таким образом вы погасите большую часть долга на раннем этапе, и эта «долговая фабрика» не сможет получать проценты в течение 30 дней. Предположим, APY по кредиту составляет 6%, а ежемесячный платеж составляет 2000 долларов. Выплатив в начале месяца, вы сэкономите \ $ 2000 * 6% = \ $ 120 / год, или \ $ 3600 в течение 30-летней ипотеки. А несколько штук — не к чему чихать.
Что делать: несколько мелких платежей или один крупный платеж? .7 $ и последний платеж проценты не начисляются. Независимо от деталей, предоплата сэкономит вам деньги.

Общий принцип: При инвестировании получайте проценты раньше, чтобы они могли увеличиваться. При заимствовании выплатите долг досрочно по номеру , чтобы не допустить начисления процентов.

Вперед и вверх

Это много для одного сеанса, но я надеюсь, вы увидели общую картину:

Процентная ставка (APR) — это «скорость», с которой деньги растут .{rt} долларов США. Вселенная не особо заботится о нашем солнечном календаре.
Процентные ставки — дело сложное. В случае сомнений попросите APY и выплатите долг досрочно.

Отношение к интересу таким причудливым способом (траектории и фабрики) поможет нам понять некоторые более крутые свойства е, которые пригодятся для вычислений. Кроме того, попробуйте Правило 72, чтобы быстро вычислить влияние процентных ставок мысленно (эти инвестиции с 6% годовых удвоятся через 12 лет).0 = 1?)

Использование логарифмов в реальном мире

Как думать экспонентами и логарифмами

Понимание дискретного и непрерывного роста

Что на самом деле означает показатель степени?

В: Почему е особенное? (2,718 …, а не 2, 3,7 или другое число?)

Процентные ставки для малого бизнеса: сложные и простые проценты

Проценты — это цена, которую вы платите за заимствование чужих денег, но то, сколько вы в конечном итоге вернете, зависит от условий вашего кредита.Уплата простых процентов по сравнению со сложными процентами может иметь большое влияние на общую сумму, которую вы заплатите к концу срока.

Давайте подробнее рассмотрим эти методы расчета процентов, чтобы почувствовать разницу между ними.

Простые проценты

При использовании простых процентов вы применяете процентную ставку к основному остатку, что дает вам сумму процентов, которую вы будете платить в течение срока ссуды. Формула расчета простых процентов выглядит следующим образом:

Основная сумма кредита x процентная ставка x срок займа = простой процент

Вы платите проценты на единовременную выплату, что упрощает расчет.Допустим, вы хотите взять взаймы 10 000 долларов под 5% годовых сроком на 3 года. При использовании простого расчета процентов уравнение выглядит так:

10 000 долларов США x 0,05 x 3 = 1 500 долларов США

Общая сумма процентов, которую вы должны выплатить, составляет 1500 долларов США. Каждый год вы будете платить 500 долларов в виде процентов. Сложные проценты немного сложнее. Давайте взглянем.

Сложные проценты

Когда начисляются проценты, это означает, что проценты накапливаются не только на основную сумму долга, но также и на проценты, которые были выплачены в течение предыдущего периода начисления сложных процентов.Если это звучит так, как будто вы выплачиваете проценты по своим процентам, вы правы. Сложные проценты встречаются чаще, чем простые проценты, и являются наиболее частым способом расчета процентов, когда речь идет о ипотеке, автокредитах, ссуде для физических лиц и малом бизнесе.

Сложные проценты могут быть хорошими или плохими в зависимости от того, на каком конце транзакции вы находитесь. Если вы являетесь кредитором, вы выиграете от получения более крупного погашения, так как с ваших процентов начисляются проценты.

Какую пользу вам могут принести сложные проценты? Рассмотрим свой сберегательный счет.Банк выплачивает вам проценты, и они становятся частью вашего общего баланса. В следующий раз, когда банк будет рассчитывать проценты, он применит процентную ставку к общей сумме денег на вашем счете, включая прошлые суммы процентов, которые они вам уже выплатили.

Если вы заемщик, этот сценарий работает в обратном порядке. Когда вы платите проценты по кредиту, их взимает банк. В следующий раз, когда вы сделаете платеж, вы заплатите проценты с этих процентов. Вот уравнение для расчета сложных процентов:

A = P (1 + r / n) ^нт

A = общая сумма, которую вы заплатите в течение срока кредита
P = основная сумма
r = процентная ставка
n = количество начислений процентов за год-12, если ежемесячно
nt = количество начисленных процентов за весь срок кредита (12, если ежемесячно, умноженное на количество лет вашего срока.)

Используя наш предыдущий пример заимствования 10 000 долларов США под 5% годовых сроком на 3 года, давайте подставим цифры и посмотрим, что мы получим:

11 614,72 долл. США = 10 000 долл. США (1 + 0,05 / 12) ³⁶

Вы также можете ввести переменные в этот калькулятор процентов, чтобы получить ту же сумму процентов. При использовании этого калькулятора убедитесь, что ваш «тип процентов» установлен на сложный и что вы выбрали правильную «частоту начисления процентов».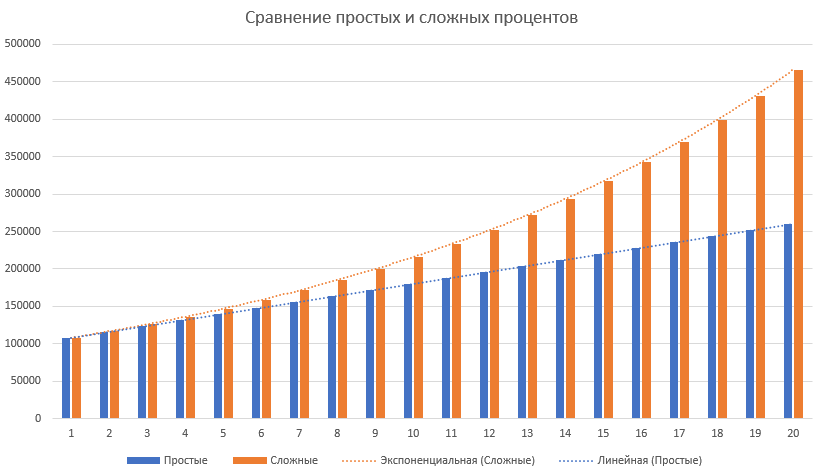 В приведенном выше примере вам нужно установить ежемесячную частоту начисления сложных процентов.

Давайте попробуем другой пример. Если вы одалживаете 7000 долларов под 12% годовых сроком на 2 года, вы можете ввести эти числа в калькулятор и увидеть, что вы заплатите 1888,14 доллара в виде процентов на общую сумму 8888,14 доллара в течение срока ссуды.

Как видите, при начислении процентов вы заплатите больше, чем если бы вы использовали простую формулу процента.Количество периодов начисления сложных процентов имеет большое значение. Чем чаще начисляются проценты, тем больше сумма сложных процентов.

Как узнать, сколько стоит мой заем?

Когда вы берете ссуду, вам будет предоставлена справка о предоставлении кредита, в которой полностью указаны ваши расходы по займу. Вы также получите график погашения с указанием суммы основного долга и процентов, составляющих каждый платеж, с указанием того, как ссуда будет выплачена полностью к концу срока ее действия.

В зависимости от того, как часто кредитор начисляет проценты и как они структурируют вашу выплату, это влияет на сумму денег, которую вы вкладываете в выплату процентов по сравнению с основной суммой. Часть каждого платежа применяется как к основной сумме, так и к процентам, однако сумма, применяемая к основной сумме, меняется каждый раз, а оставшаяся часть идет на проценты.

Узнайте об условиях займа

Как мы узнали, простые процентные ставки несложно вычислить, а сложные процентные ставки сложнее.Перед тем как взять на себя обязательство, важно понять условия своего кредита, чтобы убедиться, что вы можете позволить себе максимальную стоимость кредита.

Простые и сложные проценты — математика для нашего мира

Результаты обучения

Расчет единовременных простых процентов и простых процентов с течением времени
Определить APY с учетом процентного сценария
Расчет сложных процентов

Мы должны работать с деньгами каждый день. В то время как баланс вашей чековой книжки или подсчет ваших ежемесячных расходов на эспрессо требует только арифметики, когда мы начинаем экономить, планируем выход на пенсию или нам нужен кредит, нам нужно больше математики.

Простые проценты

Обсуждение процентов начинается с основной суммы или суммы, с которой начинается ваш счет. Это могут быть стартовые инвестиции или стартовая сумма кредита. Проценты в простейшей форме рассчитываются как процент от основной суммы долга.Например, если вы взяли взаймы 100 долларов у друга и согласились выплатить их под 5% годовых, тогда сумма процентов, которую вы заплатите, будет всего лишь 5% от 100: 100 долларов (0,05) = 5 долларов. Общая сумма, которую вы должны выплатить, составит 105 долларов, включая первоначальную основную сумму плюс проценты.

Простые разовые проценты

(1)

Примеры

Друг просит одолжить 300 долларов и соглашается выплатить его в течение 30 дней под 3% годовых. Сколько процентов вы заработаете?

Решение:

(3)

= 300 долларов США

основной

r = 0.03

3% ставка

I = 300 долларов (0,03) = 9 долларов.

Вы получите проценты в размере 9 долларов США.

В следующем видео подробно рассматривается этот пример.

Одноразовые простые проценты обычно используются только для чрезвычайно краткосрочных кредитов. По долгосрочным займам проценты обычно выплачиваются ежедневно, ежемесячно, ежеквартально или ежегодно. В этом случае проценты будут начисляться регулярно.

Например, облигации — это, по сути, ссуды, предоставленные эмитенту облигаций (компании или правительству) вами, держателем облигации. В обмен на ссуду эмитент соглашается выплачивать проценты, часто ежегодно. Облигации имеют дату погашения, когда эмитент выплачивает первоначальную стоимость облигации.

Упражнения

Предположим, ваш город строит новый парк и выпускает облигации, чтобы собрать деньги на его строительство. Вы получаете облигацию на сумму 1000 долларов, по которой выплачивается 5% годовых со сроком погашения 5 лет.Сколько процентов вы заработаете?
[show-answer q = ”14596 ″] Показать решение [/ show-answer]
[hidden-answer a =” 14596 ″] Каждый год вы будете зарабатывать 5% процентов: 1000 долларов (0,05) = 50 долларов процентов. Таким образом, в течение пяти лет вы заработаете в общей сложности 250 долларов в виде процентов. Когда наступит срок погашения облигации, вы получите обратно 1000 долларов, которые вы изначально заплатили, в результате чего у вас останется 1250 долларов. [/ Hidden-answer]

Дальнейшее объяснение решения этого примера можно увидеть здесь.

Мы можем обобщить эту интересную идею с течением времени.

Простой процент с течением времени

(4)

Единицы измерения времени (годы, месяцы и т. Д.) Должны соответствовать периоду времени для процентной ставки.

APR — Годовая процентная ставка

Процентные ставки обычно задаются как годовая процентная ставка (APR) — общая процентная ставка, которая будет выплачиваться в течение года. Если проценты выплачиваются меньшими временными интервалами, годовая процентная ставка будет разделена.

Например, ежемесячная выплата 6% годовых будет разделена на двенадцать 0.5% выплаты.

Ежеквартальная ставка 4%, выплачиваемая ежеквартально, будет разделена на четыре выплаты по 1%.

Пример

Казначейские облигации

(казначейские ноты) — это облигации, выпущенные федеральным правительством для покрытия его расходов. Предположим, вы получаете казначейские облигации на сумму 1000 долларов США с годовой ставкой 4%, выплачиваемой раз в полгода, со сроком погашения через 4 года. Сколько процентов вы заработаете?

Решение:

Поскольку проценты выплачиваются раз в полгода (два раза в год), процентная ставка 4% будет разделена на две выплаты по 2%.

(6) = 1000 долларов США	основной
r = 0,02	Ставка 2% за полгода
т = 8	4 года = 8 полугодий
I = 1000 (0,02) (8) = 160 долларов.	Вы заработаете 160 долларов в течение четырех лет.

Это видео объясняет решение.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Попробуй

Кредитная компания взимает 30 долларов за ссуду на один месяц в размере 500 долларов. Найдите годовую процентную ставку, которую они взимают.

Решение:

I = 30 долларов процентов
= 500 долларов основной суммы
r = неизвестно
t = 1 месяц

Используя, получаем. Решая, получаем r = 0,06, или 6%. Поскольку время было ежемесячным, это ежемесячные проценты.Годовая ставка будет в 12 раз больше: 72% годовых.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Сложные проценты

С простым процентом мы предположили, что получили проценты, когда получили их. На стандартном банковском счете любые проценты, которые мы зарабатываем, автоматически добавляются к нашему балансу, и мы будем получать проценты с этих процентов в будущие годы. Это реинвестирование процентов называется , составляющим .

Предположим, что мы помещаем 1000 долларов на банковский счет с ежемесячной ставкой 3% годовых. Как наши деньги будут расти?

3% годовых — это годовая процентная ставка (APR) — общая сумма процентов, подлежащих выплате в течение года. Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать 3% ÷ 12 = 0,25% в месяц.

В первый месяц

P ₀ = 1000 долларов США
r = 0,0025 (0,25%)
I = 1000 долларов США (0,0025) = 2,50 доллара США
A = 1000 USD + 2,50 USD = 1002,50 USD

В первый месяц заработаем 2 доллара.50 процентов, увеличивая баланс нашего счета до 1002,50 долларов США.

Во второй месяц

P ₀ = 1002,50 долларов США
I = 1002,50 USD (0,0025) = 2,51 USD (округлено)
A = 1002,50 доллара + 2,51 доллара = 1005,01 доллара

Обратите внимание, что во второй месяц мы заработали больше процентов, чем в первый месяц. Это потому, что мы заработали проценты не только на первоначальную 1000 долларов, которые мы вложили, но также получили проценты на 2 доллара. 50 процентов мы заработали в первый месяц. Это ключевое преимущество, которое дает нам , составляющая процентов.

Подсчет еще нескольких месяцев дает следующее:

Месяц	Начальное сальдо	Полученные проценты	Конечное сальдо
1	1000,00	2,50	1002,50
2	1002.50	2,51	1005.01
3	1005.01	2,51	1007,52
4	1007,52	2,52	1010.04
5	1010.04	2,53	1012,57
6	1012,57	2,53	1015.10
7	1015.10	2,54	1017.64
8	1017,64	2,54	1020,18
9	1020,18	2,55	1022,73
10	1022,73	2,56	1025. 29
11	1025.29	2,56	1027,85
12	1027,85	2,57	1030,42

Мы хотим упростить процесс расчета сложных процентов, потому что создание таблицы, подобной приведенной выше, требует времени.К счастью, математика хороша в том, что дает вам короткие пути. Чтобы найти уравнение, представляющее это, если P _m представляет сумму денег через m месяцев, то мы могли бы написать рекурсивное уравнение:

P ₀ = 1000 долларов США

P _м = (1 + 0,0025) P _м-1

Вы, вероятно, узнаете в этом рекурсивную форму экспоненциального роста. Если нет, мы проделаем шаги, чтобы построить явное уравнение для роста в следующем примере.

Пример

Постройте явное уравнение для роста 1000 долларов, депонированных на банковском счете с ежемесячной ставкой 3% годовых.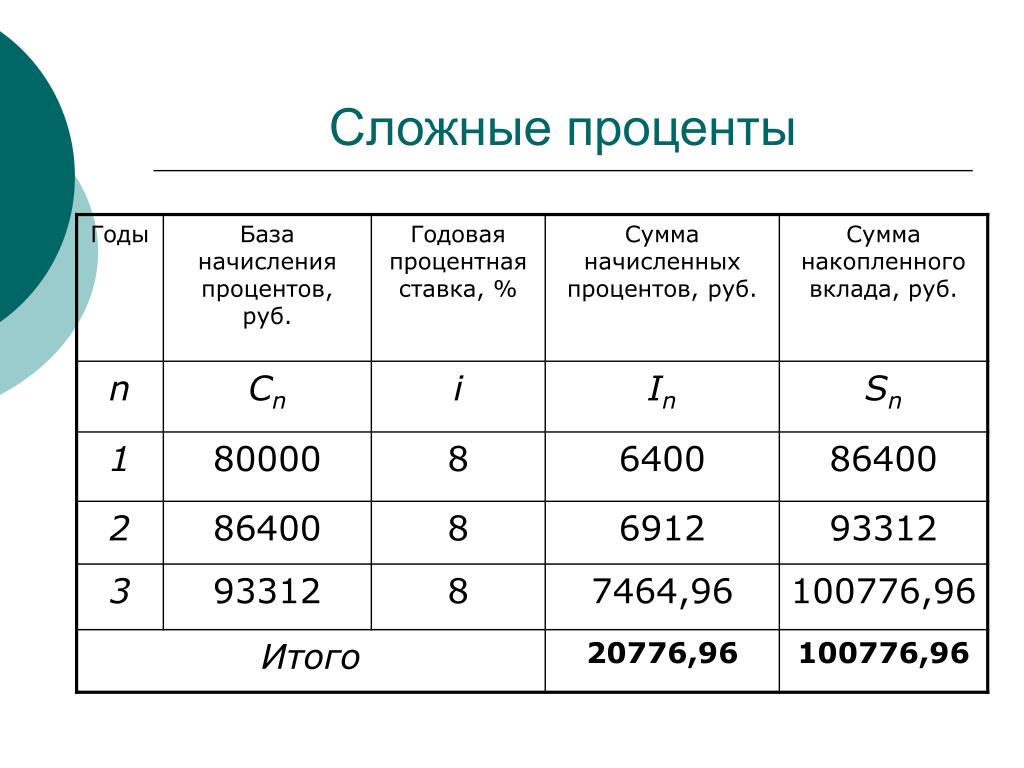

Решение:

P ₀ = 1000 долларов США
P ₁ = 1,0025 P ₀ = 1,0025 (1000)
P ₂ = 1,0025 P ₁ = 1,0025 (1,0025 (1000)) = 1,0025 2 (1000)
П ₃ = 1.0025 P ₂ = 1,0025 (1,00252 (1000)) = 1,00253 (1000)
P ₄ = 1,0025 P ₃ = 1,0025 (1,00253 (1000)) = 1,00254 (1000)

Наблюдая закономерность, можно сделать вывод

Обратите внимание, что 1000 долларов в уравнении были P ₀ , начальной суммой. Мы нашли 1,0025, прибавив единицу к скорости роста, разделенной на 12, так как мы увеличивали 12 раз в год.

Обобщая наш результат, мы можем написать

В этой формуле:

м — количество периодов начисления сложных процентов (в нашем примере месяцев)
r — годовая процентная ставка
k — количество соединений в год.

Просмотрите это видео, чтобы ознакомиться с концепцией сложных процентов.

Хотя эта формула работает нормально, чаще используется формула, которая включает количество лет, а не количество периодов сложения. Если N — количество лет, то m = N k . Это изменение дает нам стандартную формулу для сложных процентов.

Сложные проценты

P _N — остаток на счете после N лет.
P ₀ — начальный баланс счета (также называемый начальным депозитом или основной суммой)
r — годовая процентная ставка в десятичной форме
k — количество периодов начисления сложных процентов в году
- Если начисление процентов производится ежегодно (один раз в год), k = 1.
- Если начисление сложных процентов производится ежеквартально, тыс. = 4.
- Если начисление процентов производится ежемесячно, тыс. = 12.
- Если начисление сложных процентов производится ежедневно, тыс. = 365.

Самое важное, что нужно помнить при использовании этой формулы, — это то, что она предполагает, что мы помещаем деньги на счет один раз и позволяем им оставаться там, получая проценты.

В следующем примере мы покажем, как использовать формулу сложных процентов, чтобы найти остаток на депозитном сертификате через 20 лет.

Пример

Депозитный сертификат (CD) — это сберегательный инструмент, который предлагают многие банки.Обычно он дает более высокую процентную ставку, но вы не можете получить доступ к своим инвестициям в течение определенного периода времени. Предположим, вы вкладываете 3000 долларов в компакт-диск с ежемесячной выплатой 6% годовых. Сколько у вас будет на счету через 20 лет?

Решение:

В этом примере

P ₀ = 3000 долларов США	начальный депозит
r = 0,06	6% годовых
к = 12	12 месяцев в 1 год
N = 20	, поскольку мы ищем, сколько у нас будет через 20 лет

Итак (округлите ответ до ближайшего пенни)

Видео прохождение этого примера проблемы доступно ниже.

Давайте сравним сумму денег, полученных от начисления сложных процентов, с суммой, которую вы заработали бы от простых процентов

Годы	Простые проценты (15 долларов в месяц)	6% начисленных ежемесячно = 0,5% ежемесячно.
5	$ 3900	$ 4046,55
10	$ 4800	$ 5458,19
15	$ 5700	$ 7362.28
20	$ 6600	$ 9930.61
25	$ 7500	$ 13394.91
30	$ 8400	$ 180 67,73
35	$ 9300	$ 24370,65

Как видите, в течение длительного периода времени начисление сложных процентов сильно влияет на баланс счета. Вы можете понять разницу между линейным и экспоненциальным ростом.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Пример

Вы знаете, что вам понадобится 40 000 долларов на образование вашего ребенка через 18 лет. Если ваш счет зарабатывает 4% в квартал, сколько вам нужно будет внести сейчас, чтобы достичь своей цели?

Решение:

В этом примере мы ищем P ₀ .

r = 0,04	4%
к = 4	4 квартала за 1 год
N = 18	Так как мы знаем баланс за 18 лет
P ₁₈ = 40 000 долларов США	Сумма у нас за 18 лет

В этом случае нам нужно будет составить уравнение и решить для P ₀ .

(7)

Итак, вам нужно будет внести 19 539,84 доллара сейчас, чтобы иметь 40 000 долларов через 18 лет.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Округление

Если вы не вводите всю свою формулу в Desmos и выбираете делать это по частям, важно быть очень осторожным с округлением при вычислении значений с экспонентами. В общем, вы хотите использовать как можно больше десятичных знаков во время вычислений. Убедитесь, что в сохранено не менее 3 значащих цифр (числа после любых ведущих нулей). Округление от 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше сохранить больше цифр.

Пример

Чтобы понять, почему так важно не завышать округление, если вы решите не вводить свою формулу сразу в Desmos, предположим, что вы инвестируете 1000 долларов под 5% -ную ставку ежемесячно в течение 30 лет.

P ₀ = 1000 долларов США	начальный депозит
r = 0.05	5%
к = 12	12 месяцев в 1 год
N = 30	, так как мы ищем сумму через 30 лет

Если мы сначала вычислим r / k , мы найдем 0,05 / 12 = 0,00416666666667

Вот результат округления до разных значений:

r / k округлено до:	*Возвращает P30* к:**	Ошибка
0. 004	4208,59	259,15 долл. США
0,0042	$ 4521,45	$ 53,71
0,00417	4473,09 долл. США	$ 5,35
0,004167	4468,28 долл. США	0,54 доллара США
0,0041667	4467,80	0,06 доллара США
без округления	4467,74

Если вы работаете в банке, вы, конечно, вообще не станете округлять.Для наших целей ответ, который мы получили путем округления до 0,00417, трех значащих цифр, достаточно близок — 5 долларов от 4500 долларов — это неплохо. Конечно, сохранение четвертого десятичного знака не повредило бы.

Просмотрите следующее для демонстрации этого примера.

Использование калькулятора Desmos

Во многих случаях вы можете полностью избежать округления, введя значения в калькулятор. Например, в приведенном выше примере нам нужно было вычислить

Мы можем быстро вычислить это на калькуляторе Desmos, введя формулу сразу:

Чтобы ввести это в калькулятор, введите следующее:

1000 * (1 +.05/12) a ^b (12 * 30)

Примечание: a ^b находится в первой строке, втором столбце главного меню выше. Теперь вы можете округлить окончательный ответ до ближайшего цента.

Атрибуции

В этой главе содержится материал, взятый из Math in Society (в OpenTextBookStore) Дэвида Липпмана и используется по лицензии CC Attribution-Share Alike 3.0 United States (CC BY-SA 3.0 US).

Эта глава содержит материал, взятый из книги Math for the Liberal Arts (по Lumen Learning) компании Lumen Learning, и используется по лицензии CC BY: Attribution .

Является ли ипотека на недвижимость простым или сложным процентом?

Я посмеялся, читая эту эпическую ветку обсуждения на инвестиционном форуме Bogleheads: Использует ли ипотечный кредит простой или сложный процент?

Это похоже на вопрос, основанный на фактах, например, «Майами расположен к северу или к югу от Бостона?» Ответ не должен быть двусмысленным, предметным мнением или толкованием. Вы смотрите на карту и говорите «юг», и все соглашаются. Тем не менее, когда я пишу это, появилось более 100 ответов, и их количество продолжает расти, от самых умных людей, предлагающих противоположные ответы, с помощью графиков, математических уравнений и числовых примеров.Некоторые говорят, что это простой интерес; некоторые говорят, что это сложные проценты.

Кто-то ответил, что это ссуда со сложными процентами , которая не составляет . Если это не сложное, то делает ли это простым? Или это как разница между 0 и нулем?

Чтобы ответить на вопрос, нам сначала нужно понять, что такое ссуда под простые проценты, что такое ссуда со сложными процентами и каковы характеристики каждой из них.

Простая процентная ссуда

В простой процентной ссуде на проценты во втором периоде не влияют проценты за предыдущий период.Предположим, у нас есть трехлетняя ссуда с простой процентной ставкой в размере 100 000 долларов США под 1% годовых. Процентная ставка за каждый из 3 лет составляет 1 000 долларов США, всего 9 0006 3 000 9 0007 долларов США.

Если процентная ставка составляет 2% в год, процентная ставка в течение срока ссуды составит 6 000 долларов США , что ровно вдвое больше, чем по ссуде с 1% годовых.

Если ставка по-прежнему составляет 1% в год, но срок ссуды составляет 6 лет вместо 3 лет, общая сумма процентов в течение срока ссуды также удваивается.

То же самое и с ссудой 3% или ссудой на 9 лет.Вы просто умножаете основную сумму на ставку и годы, чтобы получить общую сумму процентов.

Заем под сложный процент

В ссуде со сложными процентами невыплаченные проценты в конце первого периода добавляются к основной сумме долга за второй период, что позволяет увеличивать проценты. В трехлетнем ссуде со сложными процентами в размере 100 000 долларов США и годовой процентной ставкой 1% процентная ставка за первый год составляет 1000 долларов США, за второй год — 1010 долларов США, за третий год — 1020,10 долларов США, что в сумме составляет долларов США 3 030,10 долларов США. Это больше, чем общая сумма процентов, уплаченных по сопоставимой простой процентной ссуде.

Если процентная ставка вдвое выше и составляет 2%, общая сумма процентов за весь срок действия ссуды составляет 6 120,80 долларов США , что более чем в два раза превышает общую процентную ставку по ссуде 1%, из-за начисления процентов.

Если срок ссуды вдвое больше — 6 лет под 1% процентной ставки, общая сумма процентов за весь срок ссуды составит 6152 долларов США , что также более чем в два раза превышает общую процентную ставку по 3-летней ссуде в то же время. ставка, опять же из-за начисления процентов.

Более высокая ставка или более длительный срок по ссуде со сложными процентами стоит больше, чем просто прямой мультипликатор.

Ипотечный дом

В обычной ипотеке на жилье ваш ежемесячный платеж сначала покрывает проценты за этот месяц, а оставшаяся сумма применяется к основной сумме долга. На следующий месяц проценты не прибавляются к основной сумме долга. Это привело к ответу, что это ссуда со сложными процентами , которая не составляет , потому что вы выплачиваете проценты за каждый месяц в полном объеме, а в следующем месяце ничего не остается.

Если ипотека является процентной — да, такие ипотеки есть — она ведет себя точно так же, как простая процентная ссуда. Если ставка в два раза выше, общая сумма процентов за каждый период и в течение срока кредита будет в два раза больше. Если срок ссуды вдвое больше, а ставка такая же, общая сумма процентов за весь срок ссуды также будет вдвое больше.

Выплаты основного долга

Выплата основной суммы долга по графику погашения усложняет задачу. Несмотря на то, что проценты по-прежнему не переносятся из месяца в месяц — и если вы пропустите платеж, с вас не начисляются дополнительные проценты в следующем месяце — ссуда больше не ведет себя как простая ссуда под проценты.

Увеличение процентной ставки более чем вдвое увеличивает общую сумму процентов в течение срока кредита. Общая процентная ставка по 30-летней ипотеке под 8% составляет в 2,3 раза больше , чем по 30-летней ипотеке под 4%.

Удвоение срока ссуды также более чем вдвое увеличивает общую сумму процентов в течение срока ссуды. Общая процентная ставка по 30-летней ипотеке под 4% составляет в 2,2 раза больше, чем процентов по 15-летней ипотеке с той же ставкой.

Досрочное внесение основного платежа имеет эффект накопления.Если вы заплатите 1000 долларов дополнительно в 13-м месяце, вы не только перестанете выплачивать проценты на эту 1000 долларов, но и приведет к тому, что больше ваших последующих регулярных платежей будет направлено на основную сумму, что еще больше снизит выплачиваемые вами проценты.

Эти характеристики делают типичную ипотеку с амортизированными выплатами больше похожей на ссуду со сложными процентами, но не делают ее таковой. Эффект начисления сложных процентов возникает из-за различных выплат основной суммы долга, а не от начисления сложных процентов .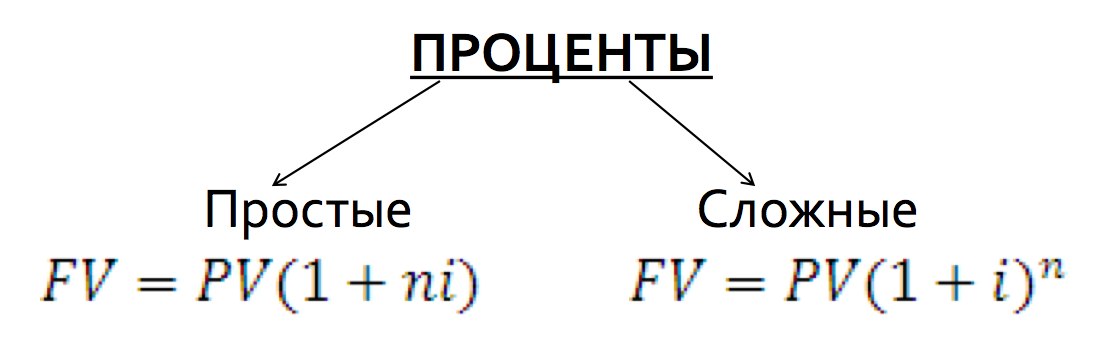

Между двумя ипотечными кредитами, если вы сохраняете основные выплаты одинаковыми, они ведут себя как простые процентные ссуды.

Если у вас есть ссуда 8% и ссуда 4%, и вы просто следуете графику погашения, вы ежемесячно платите меньше в счет основной суммы кредита по ссуде 8%, по крайней мере, в первой половине срока ссуды, даже если ваш ежемесячный платеж по ипотеке выше. Эти более низкие платежи по основному долгу усугубляются, что приводит к тому, что вы платите более чем в два раза больше общих процентов по ссуде 8% по сравнению с ссудой 4%.

Если вы фактически сохраните основные платежи на том же уровне, выполнив дополнительные основные платежи по ссуде 8%, ваша ссуда 8% будет ровно в два раза дороже, чем ссуда 4%, но не более чем в два раза.Это классическая черта простой процентной ссуды.

Заключение

Типичная ипотечная ссуда — это все еще простая процентная ссуда , даже если она похожа на сложные проценты. Ощущение начисления процентов возникает из-за различных основных выплат.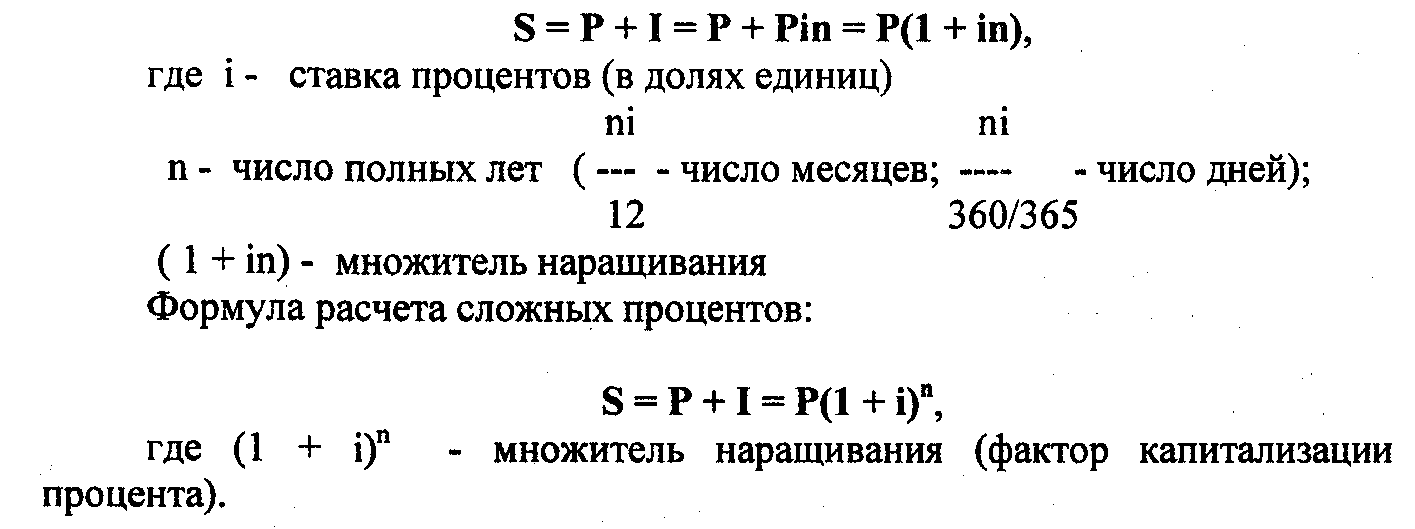 Если вы не допускаете изменения основных выплат, как в случае ссуды с выплатой только процентов (нулевой основной платеж), или путем выравнивания выплат по основной сумме, проценты по самой ссуде не складываются.

Почему, казалось бы, простой вопрос, основанный на фактах, дает совершенно противоположные ответы? Потому что он фокусирует внимание людей не на том.Интерес не увеличивается. Основные выплаты делаем. Выплата основного долга в размере 1000 долларов экономит проценты на этой 1000 долларов и вызывает более высокие выплаты основного долга в следующем году и более высокие в следующем году и так далее.

Это та же ситуация, что и при вопросе о двойном налогообложении процентов по кредиту 401k. Есть два налога, не связанных между собой, и вы по-прежнему платите те же два налога, независимо от того, занимаете ли вы свой 401k или нет. Сосредоточение внимания на неправильных вещах ведет людей по неправильному пути.

Однако на практике лучше рассматривать ипотеку как сложные проценты, хотя на самом деле это не так.