75. Гидравлика: Понятие потерь давления
| 75. Гидравлика: Понятие потерь давления |
Напомним, что этот вопрос вкратце уже упоминался в разделе 18 «Проблема внезапного вскипания хладагента в жидкостной магистрали «. Чтобы пополнить наши знания в этой области, проведем небольшой мысленный опыт с помощью схем на рис. 75.1 и 75.2. Для проведения этого опыта нам потребуются ручной кран на сливной магистрали градирни, при открытии которого градирня опорожняется, и поплавковый клапан, поддерживающий постоянный уровень воды в баке градирни. На выходе из сливной магистрали в точке В (перед краном) установим манометр, проградуированный в барах. Этот манометр будет показывать нам давление в точке В. Установим также стеклянную трубку, которая будет показывать давление в точке В в метрах водяного столба (м вод. ст.), то есть высоту уровня воды, эквивалентную давлению в точке В.
На рис. 75.1 слева {схема 1) кран на сливной магистрали закрыт. Уровень воды в трубке находится на высоте 5 м, то есть давление в точке В равно 5 м вод. ст. Манометр в точке В показывает величину избыточного давления, обусловленного высо-
На рис. 75.1 справа (схема 2) кран на сливной магистрали открыт. Под действием силы тяжести, сразу же после открытия крана, вода из бака начинает сливаться. Как только вода приходит в движение, ее уровень в стеклянной трубке падает до 4,5 м: следовательно, потери давления на участке от точки А до точки В равны 5 — 4,5 = 0,5 м вод. ст. Манометр в точке В также показывает падение давления на величину потерь, которые равны 0,5 — 0,45 = 0,05 бар (то есть 0,5 м вод. ст.).
Отсюда делаем вывод: как только вода пришла в движение, появились потери давления.
Эти потери обусловлены вязкостью воды и за-висят от ее скорости. В основном, потери давления определяются силой трения движущейся воды о внутреннюю поверхность стенок трубопровода, которая имеет ту или иную шероховатость.
Потери давления растут:
► с ростом длины трубы;
► с падением внутреннего диаметра (площади проходного сечения) трубы;
► с ростом скорости воды (то есть расхода) в трубе.
Потери давления приводят к дополнительным затратам энергии. Они порождают шумы в трубопроводах и незначительный нагрев воды. Чем больше скорость воды, тем больше шум, особенно там, где поток испытывает сужения. Например, в кранах, вентилях и т.п. Этот шум может доставлять определенные неудобства в тех случаях, когда трубопроводы проложены в жилых помещениях или поблизости от них.
► Для труб с внутренним диаметром 15 мм максимальная скорость жидкости равна 0,5 м/с.
► Для труб с внутренним диаметром 80 мм максимальная скорость жидкости равна 1,2 м/с.
Такая разница в рекомендуемых значениях скоростей обусловлена следующим
В трубах диаметром 15 мм периметр поверхности трения П=1,5смх7г«5 см, площадь проходного сечения S1 « 2 см2, а в трубах диаметром 80 мм периметр поверхности трения П = 8 см х п к 25 см при площади проходного сечения S2 * 50
периметр поверхности трения возрастает в 5 раз, тогда как площадь проходного сечения увеличивается в 25 раз. В результате сила трения (а следовательно, и потери давления) в трубе диаметром 15 мм при скорости потока 0,5 м/с будет примерно такой же, как и в трубе диаметром 80 мм при скорости потока 1,2 м/с. Поэтому чем больше диаметр трубы, тем больше в ней может быть скорость потока при одной и той же величине потерь давления на трение.
| 75.1. УПРАЖНЕНИЕ 1. Оценка потерь давления |
Для оценки потерь давления, обусловленных местными сопротивлениями (повороты, тройники, запорные вентили и т.д.), принято использовать понятие эквивалентной длины. Например, можно считать, что потери давления при повороте потока на 90° эквивалентны потерям давления на трение на отрезке трубы того же диаметра длиной 0,8 м*.
Решение упражнения 1
При условии, что диаметр трубы определен правильно, можно предположить, что потери давления на трение составляют от 10 до 20 мм вод. ст. на погонный метр длины трубы. При выполнении оценки допустим, что потери давления на трение равны среднему значению указанного диапазона, то есть 15 мм вод. ст./м. В тоже время, 6 поворотов на 90° эквивалентны по величине потерь давления участку прямой трубы того же диаметра длиной 6 х 0,8 м = 4,8 м. Следовательно, полная эквивалентная длина нашей трубы будет равна 50 м + 4,8 м « 55 м. Таким образом, полные потери давления в этой трубе составят 55 м х 15 мм вод. ст/м = 825 мм вод. ст « 0,8 м вод. ст.
ВЛИЯНИЕ РАЗНОСТИ УРОВНЕЙ НА ПОТЕРИ ДАВЛЕНИЯ
Продолжим наши мысленные эксперименты. На рис. 75.5 представлены две абсолютно одинаковые схемы, отличающиеся только тем, что высота бака градирни на схеме 1 над сливным краном больше, чем высота бака на схеме 2.
Как только мы это сделаем, то сразу же увидим, что при равенстве расходов Qvl и Qv2 потери давления для обеих схем будут в точности совпадать: Ahl = Ah3.
Вывод: потери давления на трение и местные сопротивления никоим образом не зависят от разности уровней трубопровода. Они определяются только расходом жидкости, длиной трубопровода, внутренним диаметром и шероховатостью стенок трубы.
| 75.2. УПРАЖНЕНИЕ 2. Влияние потерь давления на характеристики потока |
Рассмотрим систему, представленную на рис. 75.6.
При движении воды по трубопроводу появляются потери давления АЫ, которые зависят от длины трубопровода, его диаметра и расхода воды (то есть скорости воды в трубе).
Установим на выходе из бака фильтр.
► Как изменятся потери давления Ahl?
► Как изменится скорость воды?
Решение на следующей странице…
Решение упражнения 2
Фильтр, установленный на трубопроводе (см. рис. 75.7 справа), ведет себя точно так же, как любое местное сопротивление (поворот, вентиль и др.): он является дополнительным препятствием потоку жидкости, то есть создает дополнительные потери давления при прохождении воды. Эти потери добавляются к потерям на трение. В результате полные потери давления на участке от точки С до точки В возрастут (Ah3 > Ah 1).
Теперь рассмотрим, как изменится скорость течения воды в трубе. При установке дополнительного сопротивления, например, фильтра, потери давления на отрезке С-В возрастают (Ah3 > Ah 1). Но это сопротивление также препятствует и прохождению воды (как это делал бы ручной вентиль, сопротивление которого возрастает при его закрытии): следовательно, расход воды будет уменьшаться.
При росте потерь давления в контуре расход жидкости падает. Поскольку расход падает, неизбежно снижается и скорость потока.
Обратите внимание на дополнительные условия: следует отчетливо понимать, что скорость потока воды абсолютно одинакова на входе в фильтр и на выходе из него. Поскольку внутренний диаметр трубы одинаков по всей длине, скорость будет в точности одна и та же в каждом сечении трубы.
| 75.3. УПРАЖНЕНИЕ 3. Изменение расхода при изменении скорости |
По трубе длиной 50 м с внутренним диаметром 80 мм вода течет со скоростью 1 м/с. Как по-вашему, что произойдет с расходом, если скорость удвоится?
Решение на следующей странице…
Решение упражнения 3
Мы нарушим традицию, которая действует в нашем руководстве, поскольку здесь мы вынуждены привести несложные формулы и выполнить очень простые расчеты. Пожалуйста, извините нас за это, но вопросы гидравлики довольно сложны и иногда вам могут потребоваться отдельные базовые понятия для того, чтобы разобраться в некоторых явлениях, которые, тем не менее, мы будем стараться объяснять как можно проще.
Скорость потока и расход воды находятся в тесной взаимосвязи:
Qv V х S
(м3/с) = (м/с) х (м2)
Расход = Скорость х Площадь
Рассчитаем площадь проходного сечения трубы диаметром 80 мм (см. рис. 75.9): Рис. 75.9. S = 3,14 х 0,082 / 4 = 0,005 м2.
Теперь можно найти расходы:
► Qvl = 1 м/с х 0,005 м2 = 0,005 м3/с = 0,005 х 3600 = 18 м3/ч.
► Qv2 = 2 м/с х 0,005 м2 = 0,01 м3/с = 0,01 х 3600 = 36 м3/ч.
Таким образом, для данного диаметра трубы расход прямо пропорционален скорости потока.
При удвоении скорости потока жидкости в трубе расход также удваивается.
| 75.4. УПРАЖНЕНИЕ 4. Изменение расхода при изменении диаметра трубы |
Мы только что нашли, что при скорости потока жидкости 1 м/с в трубе диаметром 80 мм расход жидкости равен 18 м3/ч.
Теперь удвоим внутренний диаметр трубы, то есть возьмем трубу с внутренним диаметром 160 мм. Чему будет равен расход жидкости в этой трубе при той же скорости потока
Решение упражнения 4
При скорости потока 1 м/с расход в трубе с внутренним диаметром 80 мм равен 18 м3/ч. Если внутренний диаметр трубы будет равен 160 мм, то площадь ее проходного сечения станет S = 3,14 х 0,1 б2 / 4 = 0,02 м2. При скорости потока 1 м/с расход в этой трубе будет равен 1 х 0,02 = 0,02 м3/с или 0,02 х 3600 = 72 м3/ч вместо прежних 18 м3/ч. Иначе говоря, расход вырастет в 4 раза.
Внимание! Не путайте понятие «внутренний диаметр » и площадь проходного сечения: если диаметр удваивается, то площадь проходного сечения увеличивается в 4 раза!
СООТНОШЕНИЕ МЕЖДУ РАСХОДОМ И ДАВЛЕНИЕМ
Рассмотрим поплавковый клапан, предназначенный для подачи водопроводной воды в бак градирни (см. рис. 75.11). Допустим, что полностью открытый клапан при давлении воды в сети 2 бара обеспечивает расход 10 л/мин.
Для того, чтобы удвоить расход, то есть обеспечить расход через клапан, равный 20 л/мин. необходимо давление воды в сети увеличить в 4 раза.
Запомните! При слабом давлении воды в водопроводной сети расход будет небольшим. Чтобы удвоить расход, давление в сети нужно повысить в 4 раза.
Разумеется, что на практике для удвоения расхода так не поступают. Если бы на самом деле повышали давление в сети, это породило бы многие проблемы: диаметр трубопровода пришлось бы делать очень малым, вода бы в трубах сильно «гудела» и т. д.
Проведем такую аналогию: если автомагистраль загружена, то для того, чтобы повысить ее пропускную способность, водителей не заставляют ехать быстрее, а либо делают новую полосу, либо строят объездной путь! То же самое предпринимают и для увеличения расхода жидкости в трубе: увеличивают площадь проходного сечения трубы.
При заданном расходе это приводит к снижению скорости потока воды в трубе (и, следовательно, шума), а потребное для обеспечения этого расхода давление уменьшается
СООТНОШЕНИЕ МЕЖДУ РАСХОДОМ И ПОТЕРЯМИ ДАВЛЕНИЯ
В трубе с внутренним диаметром 80 мм предполагается удвоить расход. Что произойдет с потерями давления? На первый взгляд может показаться, что поскольку при удвоении расхода скорость потока удваивается, то и потери давления также должны удваиваться. К сожалению, это не так.
При удвоении расхода потери не удваиваются, а увеличиваются в четыре раза: если расход вырос в 2 раза, потери давления возрастут в 4 раза!
В примере на рис. 75.13 при скорости потока 1 м/с потери давления АР = 2 м вод. ст., а при увеличении скорости до 2 м/с потери давления умножаются на 4: АР = 2 х 4
Потери давления пропорциональны квадрату расхода.
Для получения дополнительной информации см. раздел 95 «Несколько примеров расчета потерь давления «.
| 75.5. УПРАЖНЕНИЕ 5. Изменение потерь давления при изменении расхода |
Показан участок трубопровода, пропускающий воду со скоростью I м/с. Манометры показывают давление в различных точках этого трубопровода. Из показаний манометров можно сделать следующие выводы.
При скорости водяного потока 1 м/с потери давления составляют:
— на фильтре АРф = 2 — 1,8 = 0,2 бар;
— на вентиле АРв = 1,8 — 1,7 = 0,1 бар.
Что покажут манометры на выходе из фильтра и на выходе из вентиля, если скорость потока в трубе удвоится? Решение этого упражнения приведено ниже, однако прежде, чем знакомиться с ним, попробуйте поразмышлять самостоятельно.
Решение упражнения 5
Скорость удвоилась, следовательно расход тоже удвоился. В результате потери давления на
фильтре и на вентиле вырастут в 4 раза.
Теперь потери давления на фильтре АРф = 0,2 бар х 4 = 0,8 бар, то есть манометр на выходе
из фильтра покажет 2 — 0,8 =1,2 бар.
Потери давления на вентиле АРв = 0,1 бар х 4 = 0,4 бар, то есть манометр на выходе из
вентиля покажет 1,2 — 0,4 = 0,8 бар.
Заметьте, что общие потери давления на этом участке вырастут с 0,3 до 1,2 бар: то есть тоже в 4 раза.
Измерение расхода методом перепада давления, формула
Для измерения расхода методом перепада давления существуют много различных видов устройств и приспособлений, которыми пользуются для преобразования перепада давления в сигнал расхода.
Рекомендуем разобраться с тем, что такое объемный расход и изучить каталог приборов для измерения расхода.
Устройства преобразования дельта «Р» в сигнал расхода
Тремя самыми распространенными устройствами являются манометры, мембраны и сильфоны. При помощи манометра можно снимать показание перепада давления непосредственно с прибора. Мембраны же и сильфоны можно подсоединять к контрольно-измерительным приборам.
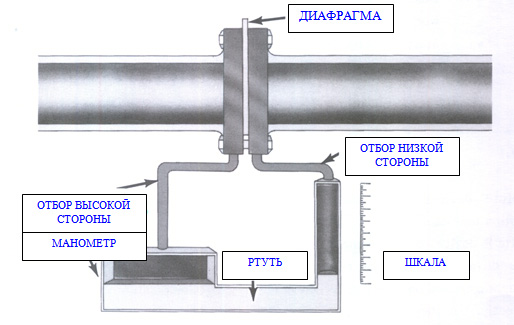Схема с манометромМанометр является одним из самых распространенных приборов, применяемых для контроля и измерения перепада давления. На изображенной схеме манометром измеряют перепад давления, созданный при помощи диафрагмы. Один конец манометра подсоединен к отбору высокой стороны, расположенному вверх по потоку относительно диафрагмы. Другой конец манометра подсоединен к отбору низкой стороны, расположенному вниз по потоку относительно диафрагмы. Во время того, как поток жидкости, газа или пара проходит через диафрагму, манометр воспринимает разницу в давлении, созданную диафрагмой, и показывает эту разницу посредством высоты жидкости в трубке. Шкала манометра позволяет снимать показание этой измеренной дельты «Р» фактически непосредственно с прибора.
Защита манометра от попадания жидкости, газа или пара из трубопровода обычно осуществляется в измерительных системах с помощью изолирующих мембран или с помощью каких-либо других способов.
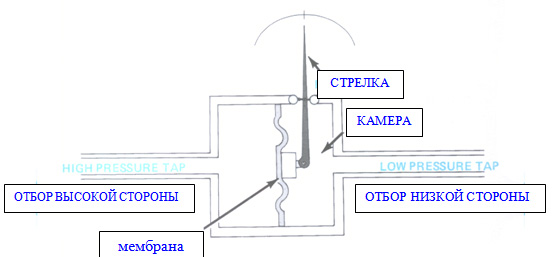Схема с мембранойНа рисунке выше изображена схема, на которой мембрана выступает в роли устройства определения дельта «Р». На этой схеме мембрана помещена в камеру, в которую имеются входы с двух сторон. Один вход подсоединен к отбору высокой стороны, а другой вход подсоединен к отбору низкой стороны. Индикаторный рычаг закреплен в верхней части камеры, а его нижний конец крепится к мембране. Разница давлений внутри камеры приводит в движение мембрану, которая, в свою очередь, приводит в движение стрелку, заставляя ее отклоняться то в одну, то в другую сторону. По мере увеличения или уменьшения величины перепада давления механическое движение мембраны передается на индикаторный рычаг.
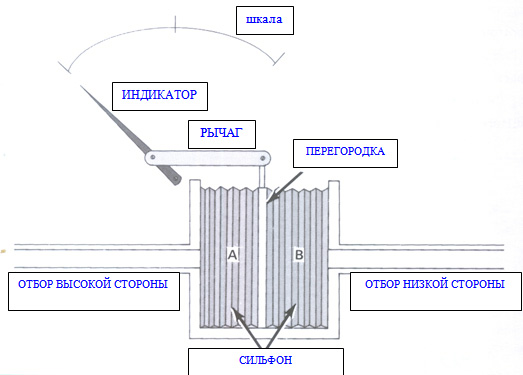Схема с двумя сильфонамиЭто схема, в которой для преобразования величины дельты «Р» в механическое движение использованы два гофрированных сильфона. Детали изображенной схемы включают в себя: два соединенных вместе сильфона с перегородкой между ними, рычаг, индикаторную стрелку и шкалу.
Сильфон, обозначенный буквой «А», подсоединяется к отбору высокой стороны, а сильфон под буквой «В» подсоединяется к отбору низкой стороны. Сильфоны помещены в камеру. Перегородка же между сильфонами может свободно перемещаться. С помощью рычага, закрепленного на перегородке, механическое движение сильфонов передается на индикаторную стрелку, которая может перемещаться вдоль шкалы.
Формула для расчета расхода на основе перепада давления
Формула для расчета расхода звучит так — величина расхода прямо пропорциональна квадратному корню отношения, измеренному в данный момент показанию дельты-Р к величине максимальной дельты-Р в процентном выражении.
Формула для преобразования разности давлений в расходДля того, чтобы преобразовать фактическое показание дельты-Р в показание расхода требуются три основные величины: величина максимального расхода в системе, величина максимального перепада давления при максимальном расходе и измеренное показание перепада давления. Упрощенной формулой, в которой для преобразования перепада давления в расход использованы эти три величины, будет следующее выражение:
Этой формулой будет легче воспользоваться, если разбить ее на три последовательных действия:
1) Разделить измеренное показание перепада давления на величину максимального перепада давления;
2) Вычислить квадратный корень от результата, полученного в первом действии;
3) Умножить полученный результат квадратного корня на величину максимального расхода. Полученный в третьем действии результат равен фактическому расходу в измеряемой системе.
Диафрагма (измерение расхода) — Википедия
У этого термина существуют и другие значения, см. Диафрагма. Схема установленной диафрагмы в кольцевой камере (которая, в свою очередь, вставлена в трубу). Принятые обозначения: 1. Диафрагма; 2. Кольцевая камера; 3. Прокладка; 4. Труба. Стрелки показывают направление жидкости/газа. Оттенками цвета выделено изменение давления.Диафра́гма (от греч. διάφραγμα — перегородка) — сужающее устройство потока газа или жидкости в трубопроводе. Является трубопроводной арматурой в качестве первичного измерительного преобразователя для измерения объёмного расхода. Представляет собой пластинчатую перегородку с отверстием внутри трубы с жидкостью или газом.
Принцип действия, как и в трубе Вентури, основан на законе Бернулли, который устанавливает связь между скоростью потока и давлением в нём. В трубопроводе, по которому протекает жидкое или газообразное вещество, устанавливается диафрагма, создающая местное сужение потока. Максимальное сжатие потока происходит на некотором расстоянии за диафрагмой, образующееся при этом минимальное сечение потока называют сжатым сечением. Вследствие перехода части потенциальной энергии давления в кинетическую средняя скорость потока в суженном сечении повышается. Статическое давление потока после диафрагмы становится меньше, чем до неё. Разность этих давлений (перепад давления) тем больше, чем больше расход протекающего вещества. Разность давлений измеряется дифференциальным манометром.
Диафрагма выполняется в виде кольца. Отверстие в центре с выходной стороны в некоторых случаях может быть скошено. В зависимости от конструкции и конкретного случая диафрагма может вставляться в кольцевую камеру или нет (см. Виды диафрагм). Материалом изготовления диафрагм чаще всего является сталь 12Х18Н10Т (ГОСТ 5632-72), в качестве материала для изготовления корпусов кольцевых камер может использоваться сталь 20 (ГОСТ 1050-88) или сталь 12Х18Н10Т (ГОСТ 5632-2014).
Течение несжимаемой жидкости через диафрагму[править | править код]
Предполагая течение жидкости, несжимаемой и невязкой, установившимся, ламинарным, в горизонтальной трубе (изменения уровня отсутствуют) с пренебрежимо маленькими потерями на трение, закон Бернулли сокращается до закона сохранения энергии между двумя точками на одной линии тока:
P1+12⋅ρ⋅V12=P2+12⋅ρ⋅V22{\displaystyle P_{1}+{\frac {1}{2}}\cdot \rho \cdot V_{1}^{2}=P_{2}+{\frac {1}{2}}\cdot \rho \cdot V_{2}^{2}}
или
P1−P2=12⋅ρ⋅V22−12⋅ρ⋅V12{\displaystyle P_{1}-P_{2}={\frac {1}{2}}\cdot \rho \cdot V_{2}^{2}-{\frac {1}{2}}\cdot \rho \cdot V_{1}^{2}}
Из уравнения неразрывности:
Q=A1⋅V1=A2⋅V2{\displaystyle Q=A_{1}\cdot V_{1}=A_{2}\cdot V_{2}} или V1=Q/A1{\displaystyle V_{1}=Q/A_{1}} и V2=Q/A2{\displaystyle V_{2}=Q/A_{2}} :
P1−P2=12⋅ρ⋅(QA2)2−12⋅ρ⋅(QA1)2{\displaystyle P_{1}-P_{2}={\frac {1}{2}}\cdot \rho \cdot {\bigg (}{\frac {Q}{A_{2}}}{\bigg )}^{2}-{\frac {1}{2}}\cdot \rho \cdot {\bigg (}{\frac {Q}{A_{1}}}{\bigg )}^{2}}
Выражая Q{\displaystyle Q_{}}:
Q=A22(P1−P2)/ρ1−(A2/A1)2{\displaystyle Q=A_{2}\;{\sqrt {\frac {2\;(P_{1}-P_{2})/\rho }{1-(A_{2}/A_{1})^{2}}}}}
и
Q=A211−(d2/d1)42(P1−P2)/ρ{\displaystyle Q=A_{2}\;{\sqrt {\frac {1}{1-(d_{2}/d_{1})^{4}}}}\;{\sqrt {2\;(P_{1}-P_{2})/\rho }}}
Указанное выше выражение для Q{\displaystyle Q} представляет собой теоретический объемный расход. Введём β=d2/d1{\displaystyle \beta =d_{2}/d_{1}}, а также коэффициент истечения Cd{\displaystyle C_{d}}:
Q=CdA211−β42(P1−P2)/ρ{\displaystyle Q=C_{d}\;A_{2}\;{\sqrt {\frac {1}{1-\beta ^{4}}}}\;{\sqrt {2\;(P_{1}-P_{2})/\rho }}}
И, наконец, введём коэффициент расхода C{\displaystyle C}, который определим как C=Cd1−β4{\displaystyle C={\frac {C_{d}}{\sqrt {1-\beta ^{4}}}}}, для получения конечного уравнения для массового расхода жидкости через диафрагму:
(1)Q=CA22(P1−P2)/ρ{\displaystyle (1)\qquad Q=C\;A_{2}\;{\sqrt {2\;(P_{1}-P_{2})/\rho }}}
Умножим полученное нами ранее уравнение (1) на плотность жидкости, чтобы получить выражение для массового расхода в любом сечении трубы:[1][2][3][4]
(2)m˙=ρQ=CA22ρ(P1−P2){\displaystyle (2)\qquad {\dot {m}}=\rho \;Q=C\;A_{2}\;{\sqrt {2\;\rho \;(P_{1}-P_{2})}}}
| где | |
| Q{\displaystyle Q_{}} | = объёмный расход (at any cross-section), м³/с |
|---|---|
| m˙{\displaystyle {\dot {m}}} | = массовый расход (at any cross-section), кг/с |
| Cd{\displaystyle C_{d}} | = коэффициент истечения, безразмерная величина |
| C{\displaystyle C} | = коэффициент расхода, безразмерная величина |
| A1{\displaystyle A_{1}} | = площадь сечения трубы, м² |
| A2{\displaystyle A_{2}} | = площадь сечения отверстия в диафрагме, м² |
| d1{\displaystyle d_{1}} | = диаметр трубы, м |
| d2{\displaystyle d_{2}} | = диаметр отверстия в диафрагме, м |
| β{\displaystyle \beta } | = соотношение диаметров трубы и отверстия в диафрагме, безразмерная величина |
| V1{\displaystyle V_{1}} | = скорость жидкости до диафрагмы, м/с |
| V2{\displaystyle V_{2}} | = скорость жидкости внутри диафрагмы, м/с |
| P1{\displaystyle P_{1}} | = давление жидкости до диафрагмы, Па (кг/(м·с²)) |
| P2{\displaystyle P_{2}} | = давление жидкости после диафрагмы, Па (кг/(м·с²)) |
| ρ{\displaystyle \rho } | = плотность жидкости, кг/м³. |
В основном, уравнение (2) применимо только для несжимаемых жидкостей. Но оно может быть модифицировано введением коэффициента расширения Y{\displaystyle Y}с целью учёта сжимаемости газов.
(3)m˙=ρ1Q=CYA22ρ1(P1−P2){\displaystyle (3)\qquad {\dot {m}}=\rho _{1}\;Q=C\;Y\;A_{2}\;{\sqrt {2\;\rho _{1}\;(P_{1}-P_{2})}}}
Y{\displaystyle Y} равен 1.0 для несжимаемых жидкостей и может быть вычислен для газов.[2]
Расчёт коэффициента расширения[править | править код]
Коэффициент расширения Y{\displaystyle Y}, который позволяет отследить изменение плотности идеального газа при изоэнтропийном процессе, может быть найден как:[2]
Y=r2/k(kk−1)(1−r(k−1)/k1−r)(1−β41−β4r2/k){\displaystyle Y=\;{\sqrt {r^{2/k}{\bigg (}{\frac {k}{k-1}}{\bigg )}{\bigg (}{\frac {\;1-r^{(k-1)/k\;}}{1-r}}{\bigg )}{\bigg (}{\frac {1-\beta ^{4}}{1-\beta ^{4}\;r^{2/k}}}{\bigg )}}}}
Для значений β{\displaystyle \beta } менее чем 0.25, β4{\displaystyle \beta ^{4}} стремится к 0, что приводит к обращению последнего члена в 1. Таким образом, для большинства диафрагм справедливо выражение:
(4)Y=r2/k(kk−1)(1−r(k−1)/k1−r){\displaystyle (4)\qquad Y=\;{\sqrt {r^{2/k}{\bigg (}{\frac {k}{k-1}}{\bigg )}{\bigg (}{\frac {\;1-r^{(k-1)/k\;}}{1-r}}{\bigg )}}}}
Подставив уравнение (4) в выражение для массового расхода (3) получим:
m˙=CA22ρ1(kk−1)[(P2/P1)2/k−(P2/P1)(k+1)/k1−P2/P1](P1−P2){\displaystyle {\dot {m}}=C\;A_{2}\;{\sqrt {2\;\rho _{1}\;{\bigg (}{\frac {k}{k-1}}{\bigg )}{\bigg [}{\frac {(P_{2}/P_{1})^{2/k}-(P_{2}/P_{1})^{(k+1)/k}}{1-P_{2}/P_{1}}}{\bigg ]}(P_{1}-P_{2})}}}
и
m˙=CA22ρ1(kk−1)[(P2/P1)2/k−(P2/P1)(k+1)/k(P1−P2)/P1](P1−P2){\displaystyle {\dot {m}}=C\;A_{2}\;{\sqrt {2\;\rho _{1}\;{\bigg (}{\frac {k}{k-1}}{\bigg )}{\bigg [}{\frac {(P_{2}/P_{1})^{2/k}-(P_{2}/P_{1})^{(k+1)/k}}{(P_{1}-P_{2})/P_{1}}}{\bigg ]}(P_{1}-P_{2})}}}
Таким образом, конечное выражение для несжатого (т.е., дозвукового) потока идеального газа через диафрагму для значений β меньших, чем 0.25:
(5)m˙=CA22ρ1P1(kk−1)[(P2/P1)2/k−(P2/P1)(k+1)/k]{\displaystyle (5)\qquad {\dot {m}}=C\;A_{2}\;{\sqrt {2\;\rho _{1}\;P_{1}\;{\bigg (}{\frac {k}{k-1}}{\bigg )}{\bigg [}(P_{2}/P_{1})^{2/k}-(P_{2}/P_{1})^{(k+1)/k}{\bigg ]}}}}
Используя уравнение состояния идеального газа и фактор сжимаемости (вносится для корректировки ввиду отличия реальных газов от идеальных), выражение для практического использования при дозвуковом потоке реального газа через диафрагму для значений β меньших, чем 0.25:[3][4][5]
(6)m˙=CA2P12MZRT1(kk−1)[(P2/P1)2/k−(P2/P1)(k+1)/k]{\displaystyle (6)\qquad {\dot {m}}=C\;A_{2}\;P_{1}\;{\sqrt {{\frac {2\;M}{Z\;R\;T_{1}}}{\bigg (}{\frac {k}{k-1}}{\bigg )}{\bigg [}(P_{2}/P_{1})^{2/k}-(P_{2}/P_{1})^{(k+1)/k}{\bigg ]}}}}
Помня что Q1=m˙ρ1{\displaystyle Q_{1}={\frac {\dot {m}}{\rho _{1}}}} и ρ1=MP1ZRT1{\displaystyle \rho _{1}=M\;{\frac {P_{1}}{Z\;R\;T_{1}}}} (уравнение состояния реального газа с учётом фактора сжимаемости)
(8)Q1=CA22ZRT1M(kk−1)[(P2/P1)2/k−(P2/P1)(k+1)/k]{\displaystyle (8)\qquad Q_{1}=C\;A_{2}\;{\sqrt {2\;{\frac {Z\;R\;T_{1}}{M}}{\bigg (}{\frac {k}{k-1}}{\bigg )}{\bigg [}(P_{2}/P_{1})^{2/k}-(P_{2}/P_{1})^{(k+1)/k}{\bigg ]}}}}
| где | |
| k{\displaystyle k} | = отношение теплоёмкостей (cp/cv{\displaystyle c_{p}/c_{v}}), безразмерная величина |
|---|---|
| m˙{\displaystyle {\dot {m}}} | = массовый расход в произвольном сечении, кг/с |
| Q1{\displaystyle Q_{1}} | = расход реального газа до диафрагмы, м³/с |
| C{\displaystyle C} | = расходный коэффициент диафрагмы, безразмерная величина |
| A2{\displaystyle A_{2}} | = площадь сечения отверстия в диафрагме, м² |
| ρ1{\displaystyle \rho _{1}} | = плотность реального газа до диафрагмы, кг/м³ |
| P1{\displaystyle P_{1}} | = давление газа до диафрагмы, Па (кг/(м·с²)) |
| P2{\displaystyle P_{2}} | = давление газа после диафрагмы, Па (кг/(м·с²)) |
| M{\displaystyle M} | = молекулярная масса газа, кг/моль (также известна как молекулярный вес) |
| R{\displaystyle R} | = универсальная газовая постоянная = 8.3145 Дж/(моль·К) |
| T1{\displaystyle T_{1}} | = абсолютная температура газа до диафрагмы, K |
| Z{\displaystyle Z} | = фактор сжимаемости газа при P1{\displaystyle P_{1}} и T1{\displaystyle T_{1}}, безразмерная величина. |
Детальное описание критического и некритического течения газов, а также выражения для критического потока газа через диафрагму можно найти в статье про критический поток.
ДКС[править | править код]
ДКС — диафрагма камерная стандартная.
Рассчитана [6] на условное давление до 10 МПа с условным проходом от 50 до 500 мм.
ДБС[править | править код]
ДБС — диафрагма бескамерная стандартная.
Рассчитана [6] на условный проход от 300 до 500 мм и условное давление до 4 МПа.
- ↑ Lecture, University of Sydney Архивная копия от 29 мая 2007 на Wayback Machine
- ↑ 1 2 3 Perry, Robert H. and Green, Don W. Perry’s Chemical Engineers’ Handbook (англ.)русск. (неопр.). — Sixth Edition. — McGraw-Hill Education, 1984. — ISBN 0-07-049479-7.
- ↑ 1 2 Handbook of Chemical Hazard Analysis Procedures, Appendix B, Federal Emergency Management Agency, U.S. Dept. of Transportation, and U.S. Environmental Protection Agency, 1989. Handbook of Chemical Hazard Analysis, Appendix B Click on PDF icon, wait and then scroll down to page 391 of 520 PDF pages.
- ↑ 1 2 Risk Management Program Guidance For Offsite Consequence Analysis, U.S. EPA publication EPA-550-B-99-009, April 1999.
Расход сжатого воздуха: особенности расчета — компрессорные, азотные, насосные станции
При работе с компрессионным оборудованием необходимо иметь представление как исчисляется расход сжатого воздуха, тем более что производительность компрессора и определяется как объем сжимаемого газа в единицу времени.
Конечно, существуют специальные контрольно-измерительные приборы, но в некоторых случаях необходимо быстро произвести расчет расхода воздуха отдельными устройствами.
Необходимо начать с того, что уточнить, в чем измеряется воздух. Объем воздуха измеряется в кубических метрах. Единицы измерения расхода воздуха исчисляются в кубических метрах (для винтовых компрессоров) или литрах (для поршневых компрессоров) потребляемого или производимого воздуха в единицу времени (м3/мин, м3/час, л/мин).
Согласно данным российского ГОСТ 12449-80 нормальными условиями считаются
- давление 101,325 кПа (760 мм. рт .ст),
- температура 293 К (20 С),
- влажность 1,205 кг/м3.
При определении расхода сжатого воздуха при нормальных условиях по ГОСТ 12449-80 перед единицей измерения сжатого воздуха ставят маркировку «н» (15нм3/мин или 165нм3/час и т.д.).
Также существуют две популярные методики расчета расхода воздуха потребляющим оборудованием.
Расчет расхода воздуха через падение давления – универсальный метод для всех видов компрессоров
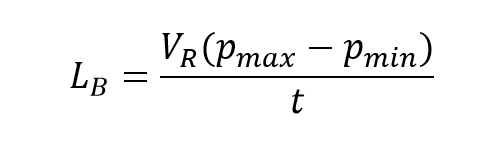
Где:
- LB — искомое потребление сжатого воздуха [м³/мин]
- VR — объем резервуара с сжатым воздухом [м³] (1 м³ = 1000 л)
- pmax — давление на время начала измерений [бар]
- pmin — давление на время окончания измерений [бар]
- t — продолжительность измерений [мин]
На начало измерения необходимо знать объем резервуара и давление в нем (показания манометра). Включаем потребляющее оборудование, засекаем время работы. Отключаем оборудование, смотрим показания манометра резервуара. Подставляем данные в формулу.
Расчет расхода через время работы компрессора – метод для компрессоров с постоянной производительностью
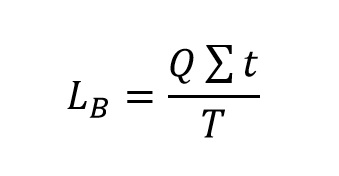
- LB — искомое потребление сжатого воздуха [м³/мин]
- Q — производительность компрессора [м³/мин]
- ∑t — время работы компрессора под нагрузкой за период измерений [мин]
- T — период измерений = время работы под нагрузкой + на холостом ходу [мин]
На начало измерения нам необходимо знать производительность компрессора, снять показания счетчика общей наработки и счетчика работы под нагрузкой. Включаем потребляющее оборудование, засекаем время работы под нагрузкой при наборе давления до максимального значения, после которого компрессор работает на холостом ходу до начала следующего набора давления. Отключаем оборудование. Подставляем данные в формулу.
Определение расхода воздуха, проходящего через пневмораспределитель при определенных значениях давления на входе и выходе и их соотношении
Одним из способов задания расходной характеристики пневматического устройства является определение параметра, характеризующего его гидравлическое сопротивление. В настоящее время таким параметром является пропускная способность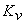 
устройства, определяемая по ГОСТ Р52720–2007 как объемный расход воды 
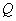(м3/час) плотностью r=1000 кг/м3, пропускаемый устройством при перепаде давления на нем 
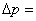1 кгс/см2.
Заметим, что параметры потока в местных сопротивлениях обычно и определяются с помощью формул, полученных для несжимаемой жидкости. Поэтому воспользуемся формулой Вейсбаха и, преобразуя ее, получим выражение для определения объемного расхода 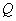жидкости при ее движении через пневмоустройство:
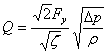, (1)
где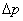 
и r — соответственно перепад давления в устройстве и плотность жидкости, протекающей через него; 
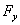— площадь поперечного сечения прохода устройства; 
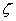— коэффициент местного сопротивления.
Если теперь принять, что через местное сопротивление проходит вода плотностью r=1000 кг/м3 с перепадом давления 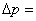1 кгс/см2, то зависимость (1) преобразуется к виду (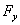,см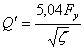2):
. (2)
В соответствии с ГОСТ Р52720–2007 правая часть формулы (2) представляет не что иное, как пропускную способность 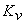(м3/час) устройства. Таким образом, в общем случае объемный расход 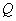(м3/час) рабочей жидкости при ее движении через распределитель следует определять по формуле:
=
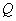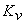
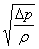, (3)
а массовый расход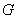 
=
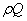(кг/час) — по формуле
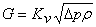. (4)
Отметим, что выражения (3) и (4) полностью согласуются с формулами для определения величины 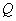и 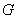, приведенными в Интернет(е) Научно-Производственным Предприятием «Волга» [2].
Как известно, в процессе работы пневматических приводов возможны различные условия теплообмена между потоком газа, движущимся в трубопроводах, и окружающей средой.
Если скорость течения газа мала и между стенками трубопровода и окружающей средой происходит хороший теплообмен, то процессы, протекающие в пневмоприводах, близки к изотермическим; при больших скоростях течения газа, плохом теплообмене и малых силах трения процессы, протекающие в пневмоприводах, близки к адиабатным.
Таким образом, если предположить, что перед и за пневматическим устройством температура воздуха одинакова (участки трубопровода перед и за местным сопротивлением достаточно велики, вследствие чего происходит полное выравнивание температуры потока и окружающей среды), то в этом случае для определения расхода воздуха в местном сопротивлении удобно воспользоваться расчетной зависимостью, полученной в [1,с.101] для подкритической области изотермического течения газа:
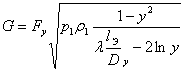(5)
или
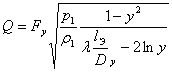, (6)
или с учетом того, что в соответствии с уравнением Клапейрона-Менделеева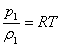 
,
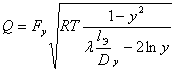, (7)
где 
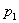и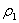 
— давление и плотность газа перед местным сопротивлением; 
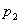— давление за местным сопротивлением; 
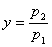— относительное давление; 
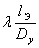— параметр, характеризующий гидравлическое сопротивление пневмоустройства условного прохода 
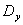, определенный через эквивалентную длину 
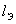трубопровода, т. е. такую длину трубы, разность давлений в начальном и конечном сечениях которой при данном расходе равна разности давлений в местном сопротивлении; 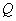— объемный расход газа; R — газовая постоянная, равная 
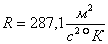, T — температура газа при нормальных условиях, равная 
.
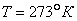Из (7) следует, что для построения расходной характеристики пневмораспределителя необходимо располагать значением параметра 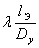. Затем, задаваясь значениями давления воздуха на входе и перепадом давления в пневмоустройстве, легко устанавливается искомая характеристика.
Будем рассматривать параметр 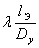как коэффициент сопротивления 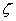устройства данного проходного сечения, установленный при турбулентном режиме течения рабочей жидкости, соответствующем области квадратичных сопротивлений, когда коэффициент местного сопротивления определяется лишь формой местного сопротивления. Но при таких режимах течения жидкости определяется пропускная способность устройства, в расчетную формулу которой входит коэффициент сопротивления 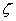. Тогда
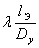= z = 
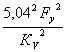, (8)
а формула (7) приводится к виду
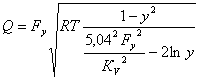. (9)
Такова расходная характеристика пневмоустройства.
В заключение отметим, что формулы (5) — (7), (9) справедливы в области изменения относительного давления «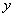
» в пределах от 
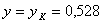до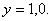 
Параметр 
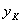называют критическим отношением давлений, при достижении которого расход газа приобретает максимальное значение и остается неизменным вплоть до значения 
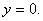В газодинамических расчетах область течения газа при 
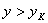называют подкритической, а область течения при 
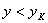надкритической. Следовательно, для подкритической области течения весовой (объемный) расход газа есть функция «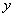»; для надкритической области течения расход имеет максимальное значение и для его определения в зависимости (5) — (7) и (9) вместо «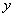» необходимо подставить .
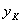Рассмотрим числовой пример. Определим расходную характеристику пневмораспределителя с условным проходом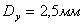 
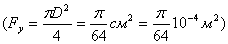, паспортной величиной 
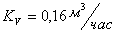. Температура воздуха в распределителе 
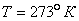; газовая постоянная 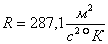. Требуется найти расход воздуха, проходящего через распределитель, при перепаде давления 
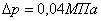с давлением на входе в распределитель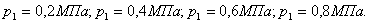 
При заданных значениях давления 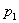воздуха на входе в распределитель давление 
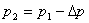на выходе устройства соответственно составит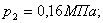 
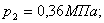
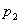=0,56МПа;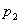=0,76МПа, а относительное давление 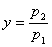соответственно принимает значения 
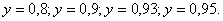Это означает, что во всем диапазоне изменения относительного давления «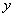», имеет место подкритическая область течения газа, расход которого можно определять по формуле (9).
Подставляя в формулу (8) значения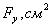 
и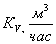 
, находим, что 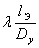=2,39, а значения объемного расхода 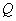, вычисленные по формуле (9) по данной величине 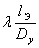для принятых значений относительного давления «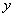», составляют: 
, 
,
.
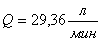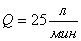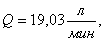
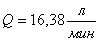Полученная расходная характеристика пневмораспределителя представлена ниже графически в виде зависимости объемного расхода газа 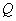от «».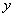
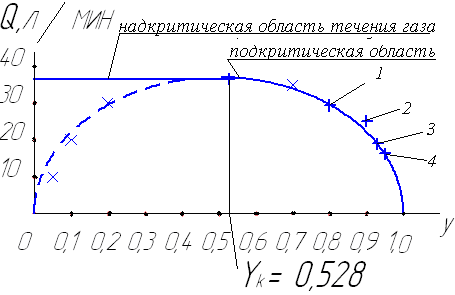
Рис.1. Расходная характеристика пневмораспределителя
Расчеты автора: + 1. y = 0,8; 2.y =0,9; 3.y = 0,93; 4. y = 0,95
Х — произвольные значения “y”
Выводы
В системах пневматических приводов, как и гидроприводов, местные сопротивления играют исключительно большую роль. От умения правильно оценить параметры потока, протекающего через местные сопротивления, зависит точность и надежность произведенных расчетов.
Местные сопротивления, как правило, способствуют турбулизации потока, вследствие чего коэффициент местного сопротивления уже при сравнительно малых числах Рейнольдса определяется лишь формой местного сопротивления, что позволяет выразить коэффициент местного сопротивления через пропускную способность устройства и тем самым построить его расходную характеристику.
Литература:
1. Погорелов В. И. Газодинамические расчеты пневматических приводов. — Л: «Машиностроение», 1971. — 184с.
2. http://www.nppvolga.ru/articles/1/63/
ДАВЛЕНИЕ В ШИНАХ И РАСХОД ТОПЛИВА — Как снизить расходы на автомобиль
ДАВЛЕНИЕ В ШИНАХ И РАСХОД ТОПЛИВА — Как снизить расходы на автомобильПравильно накачанные шины значительно снижают расход топлива и денежные затраты на ремонт автомобиля !
Подавляющее большинство автомобилей ездит с недостаточным давлением воздуха в шинах. Например, исследование, проведенное Uniroyal, обнаружило, что в Германии только около 13% автомобилей показывают корректно отрегулированное давление в шинах. Около 17% автомобилей ездит с давлением воздуха в шинах выше предписанного. Абсолютное большинство, а именно 70% всех автомобилей имело слишком низкое давление воздуха в шинах.
В любом случае постепенно, но верно давление в колесе снижается. Слегка »приспущенная» шина медленно, но верно »умирает»: при значении давления воздуха на 20% меньше нормы, срок ее службы уменьшается примерно на треть.
