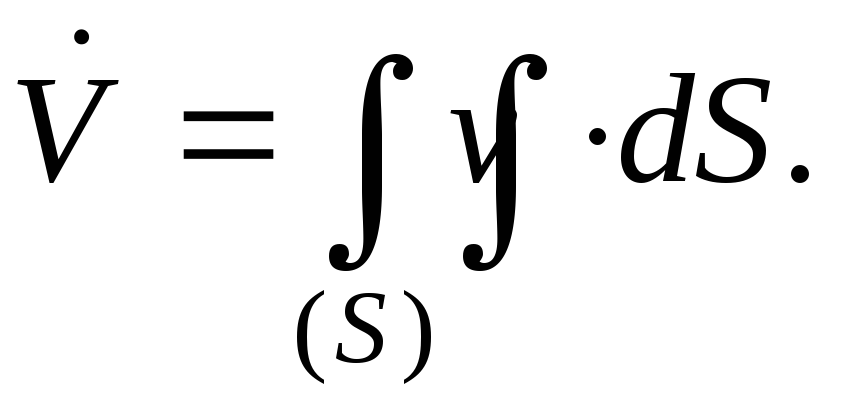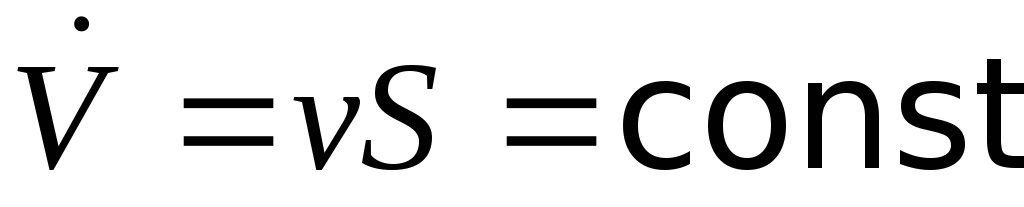13.Расход жидкости(виды расходов) и средняя скорость. Способы их определения
Расходом называется количество жидкости, протекающей через живое сечение потока в единицу времени.
Различают:
объемный (Q) :
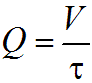
массовый (Qm) :
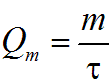
весовой (G)
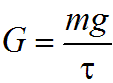
расходы жидкости. Где V— объем жидкости; m — масса жидкости; ? — время.
Объемный расход потока с живым сечением F определим с использованием понятия средней скорости потока wcp:
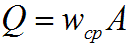
Средняя скорость — это условная скорость потока, которая считается одинаковой для всех частиц данного сечения, но подобрана так, что расход, определенный по ее значению, равен истинному значению расхода.
14. Уравнения неразрывности для элементарной струйки и потоки жидкости.
Если несжимаемая жидкость движется без разрывов, то при установившемся движении объемный расход для всех живых сечений потока постоянен, т.е. можно записать, что вдоль потока
Это уравнение называют уравнением неразрывности потока, оно является первым основным уравнением гидродинамики. Из него следует, что средние скорости обратно пропорциональны площадям соответствующих живых сечений потока.
14(2). Уравнение неразрывности для элементарной струйки и потока жидкости при установившемся движении. В гидравлике обычно рассматривают потоки, в которых не образуются разрывы и не заполненные жидкостью пустоты, т.е. жидкость сплошь заполняет пространство.
Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении. Выделим сечение 1-1 и 2-2, расположенные на расстоянии l одно от другого (рис.1.23). Здесь Δs1 и Δs2 — площади живых сечений соответственно; u 1 и u2 — скорости; ΔQ1 и ΔQ2 — расходы элементарной струйки в сечениях.
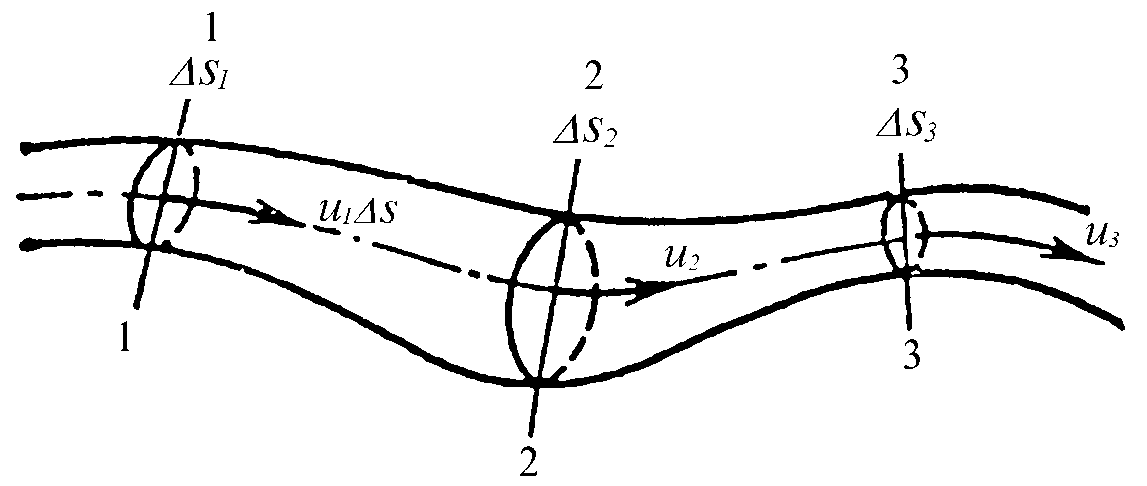
Рис. 1.23. Элементарные струйки несжимаемой жидкости при установившемся режиме движения
Очевидно, что ΔQ1 = Δs1u1 и ΔQ2 = Δs2u2, причем ΔQ1 втекает в рассматриваемый отсек, а ΔQ 2 — вытекает.
Учитывая, что форма элементарной струйки не изменяется с течением времени, поперечный приток и отток невозможен, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, получаем, что расходы ΔQ1 и ΔQ2 равны, т.е.
Δs1u 1 = Δs2u2. (1.50)
u1Δs1 = u2Δs2 =…= uΔs = ΔQ = const (1.51)
Это и есть уравнение неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении.
Если выделить в потоке два любых сечения, отстоящих на некотором расстоянии, то, просуммировав по каждому из живых сечений обе части в уравнении (1.50)

Таким образом, в отмеченных условиях расход, проходящий через все живые сечения потока, неизменен, несмотря на то что в каждом сечении средняя скорость и площадь живого сечения могут быть различны.
Из (1.52) получим также важное соотношение
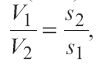
т.е. средние скорости обратно пропорциональны площадям живых сечений потока, которым соответствуют эти средние скорости.
Уравнение неразрывности (1.52) является одним из основных уравнений гидродинамики.
22. Гидравлические элементы потока
— Площадь живого сечения— площадь плоского поперечного сечения нормального к направлению движения.
— Площадь поперечного сечения струйки жидкости, перпендикулярного его линии тока называется площадью живого сечения струйки. Живое сечение потока представляет собой поверхность, проведенную перпендикулярно направлению движения жидкости и лежащую в пределах этого потока.
— Смоченный периметр— часть периметра, на котором поток соприкасается с твердыми стенками:
— Гидравлический радиус– отношение площади живого сечения к смоченному периметру:
Для круглого сечения R = π r2 / (2 π r) = r / 2 = d / 4
23. Методы определения движения жидкости (метод Лагранжа и метод Эйлера).
1. Метод Лагранжа. Этот метод не используется при описании волновых функций. Суть метода в следующем: требуется описать движение каждой частицы. Начальному моменту времени t0 соответствуют начальные координаты x0, y0, z0. Однако к моменту t они уже другие. Как видно, речь идет о движении каждой частицы. Это движение можно считать определенным, если возможно указать для каждой частицы координаты x, y, z в произвольной момент времени t как непрерывные функции от x0, y0, z0. x = x(x0, y0, z0, t) y =y (x0, y0, z0, t) z = z(x0, y0, z0, t) (1) Переменные x0, y0, z0, t, называют переменными Лагранжа.
2. Метод определения движения частиц по Эйлеру. Движение жидкости в этом случае происходит в некоторой неподвижной области потока жидкости, в котором находятся частицы. В частицах произвольно выбираются точки. Момент времени t как параметр является заданным в каждом времени рассматриваемой области, которая имеет координаты x, y, z.Рассматриваемая область, как уже известно, находится в пределах потока и неподвижна. Скорость частицы жидкости u в этой области в каждый момент времени t называется мгновенной местной скоростью.Полем скорости называется совокупность всех мгновенных скоростей. Изменение этого поля описывается следующей системой:ux = ux(x,y,z,t)uy = uy(x,y,z,t)иuz = uz(x,y,z,t)Переменные в (2) x, y, z, t называют переменными Эйлера.
24 Уравнение неразрывности (уравнение сохранения массы)
Неразрывности
уравнение (далее Н)
в гидродинамике, одно из уравнений
гидродинамики, выражающее закон
сохранения массы для любого объема
движущейся жидкости (газа). В переменных
Эйлера (см. Эйлера
уравнения гидромеханики) Н имеет вид: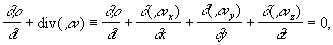 где
r — плотность жидкости, v — ее скорость в
данной точке, a vx,
vy
где
r — плотность жидкости, v — ее скорость в
данной точке, a vx,
vy
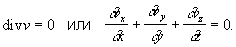 Для
установившегося одномерного течения
в трубе, канале и т.п. с площадью поперечного
сечения Н дает закон
постоянства расхода rSv = const.
Для
установившегося одномерного течения
в трубе, канале и т.п. с площадью поперечного
сечения Н дает закон
постоянства расхода rSv = const.25. Расход жидкости (массовый, объемный, весовой).
Массовый расход — масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени.
Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м
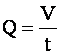 ,где Q — объёмный
расход жидкости, V — объём жидкости,
протекающий через живое сечение потока,
t – время течения жидкости.
,где Q — объёмный
расход жидкости, V — объём жидкости,
протекающий через живое сечение потока,
t – время течения жидкости.
Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле
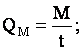 где QM — массовый
расход жидкости,
где QM — массовый
расход жидкости,
Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так:
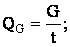 где QG — весовой
расход жидкости, G — вес жидкости,
протекающий через живое сечение потока,
t – время течения жидкости.
где QG — весовой
расход жидкости, G — вес жидкости,
протекающий через живое сечение потока,
t – время течения жидкости.
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости
2.3. Расход жидкости
Расход – это объём жидкости, протекающей сквозь воображаемую проницаемую поверхность за единицу времени.
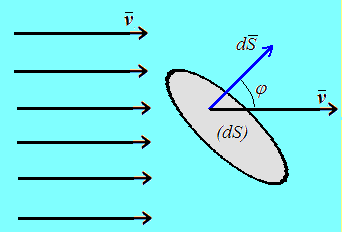
В пространство,
где течёт жидкость или газ со скоростью
поместим воображаемую неподвижную
бесконечно малую площадку проницаемую для жидкости. На
рис. 2.5 показан случай, когда
вектор
проницаемую для жидкости. На
рис. 2.5 показан случай, когда
вектор площадки располагается под
произвольным углом
площадки располагается под
произвольным углом  к вектору скорости
к вектору скорости
Расход жидкости
через площадку 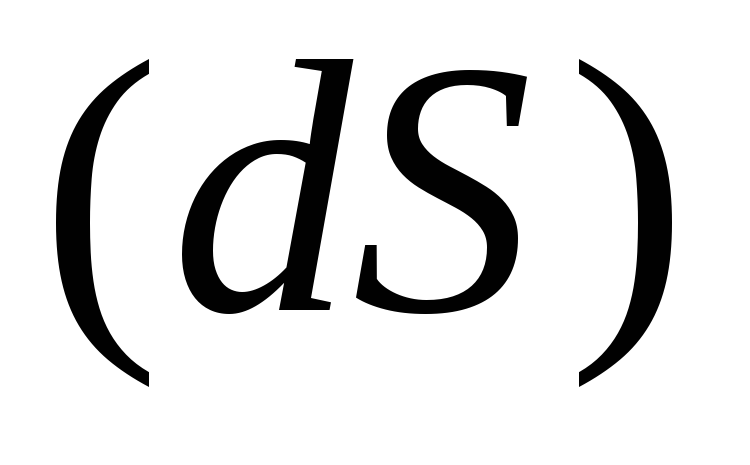 будет равен
будет равен
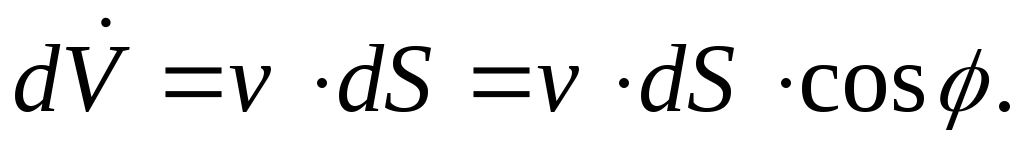
 (2.1)
(2.1)
Теперь в пространство,
где течёт жидкость или газ, поместим
произвольную поверхность 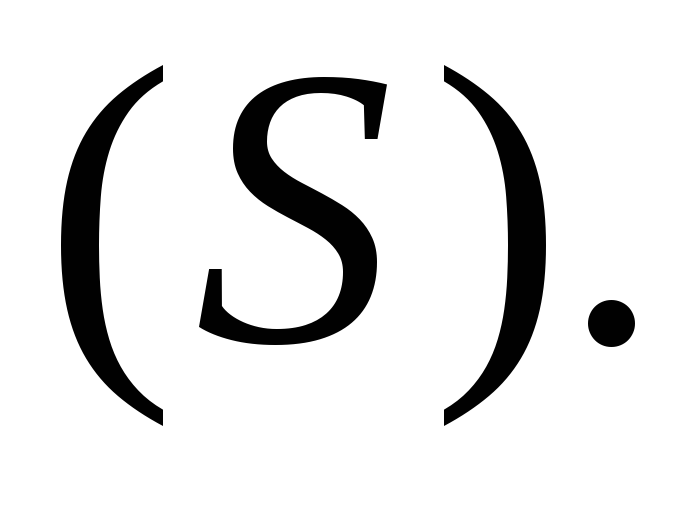 Мысленно разобьём
Мысленно разобьём на бесконечно малые части. Расход
сквозь каждую часть определяется по
формуле (2.1). Сложив (проинтегрировав)
эти расходы, получим расход через всю
на бесконечно малые части. Расход
сквозь каждую часть определяется по
формуле (2.1). Сложив (проинтегрировав)
эти расходы, получим расход через всю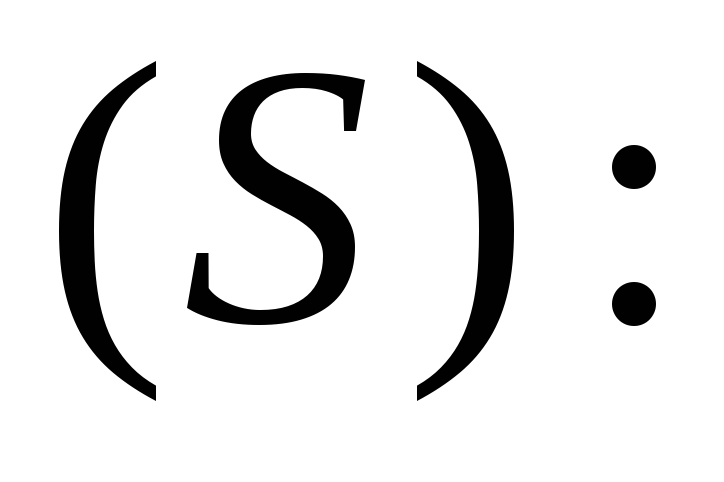 Рис.
2.5
Рис.
2.5
|
Расход
жидкости (газа) через поверхность |
(2.2)
Если сечение  перпендикулярно скорости течения:
перпендикулярно скорости течения: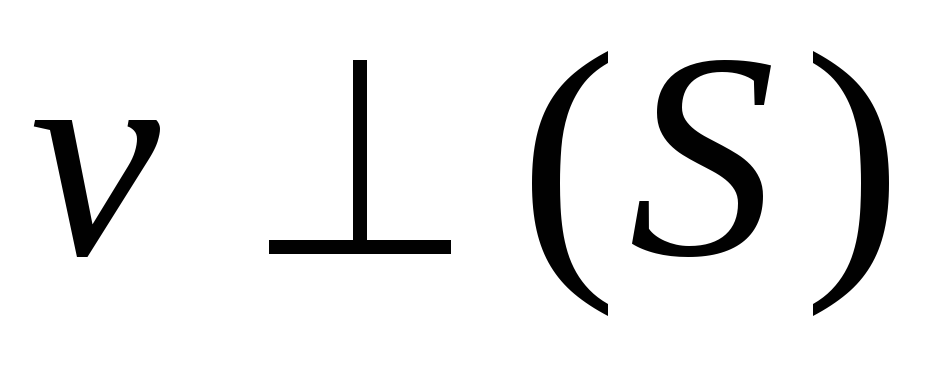 (при этом
(при этом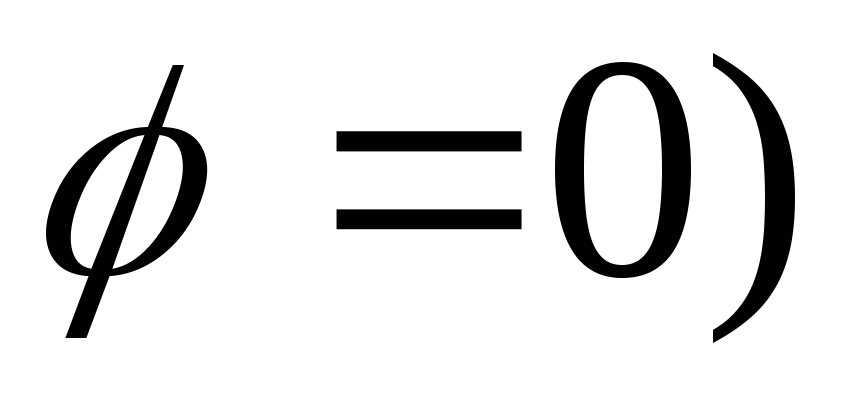 и скорость во всех точках
и скорость во всех точках одинакова, то из (2.2) будем иметь
одинакова, то из (2.2) будем иметь
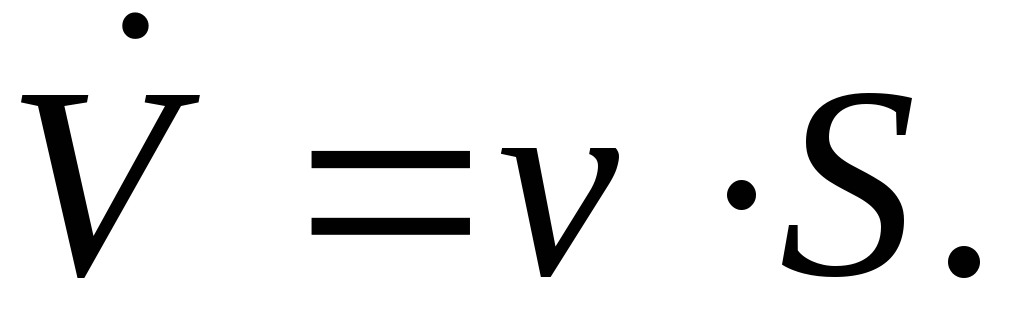 (2.3)
(2.3)
Обыкновенно этой формулой пользуются при вычислении расхода жидкости или газа через поперечное сечение трубопровода.
Умножим объём
(2.1) на плотность  Получиммассу жидкости, протекающей сквозь
Получиммассу жидкости, протекающей сквозь 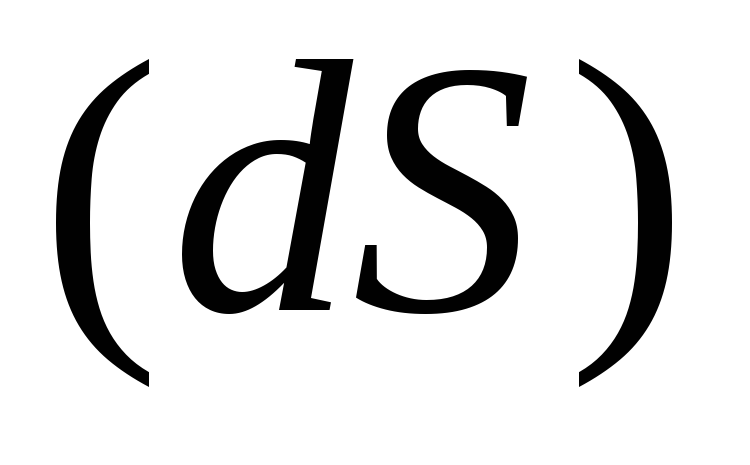 за единицу времени
за единицу времени
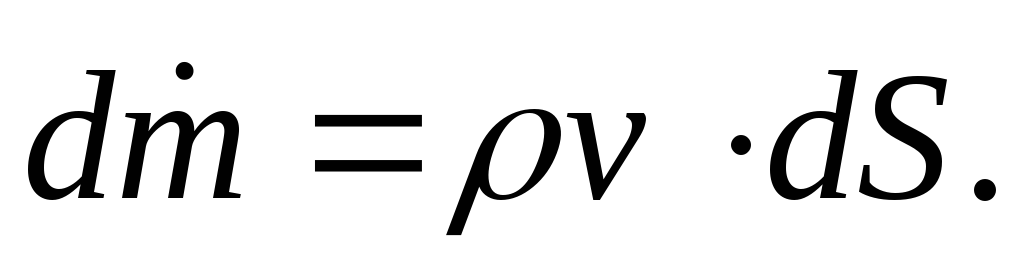 (2.4)
(2.4)
Проинтегрировав
(2.4) по поверхности 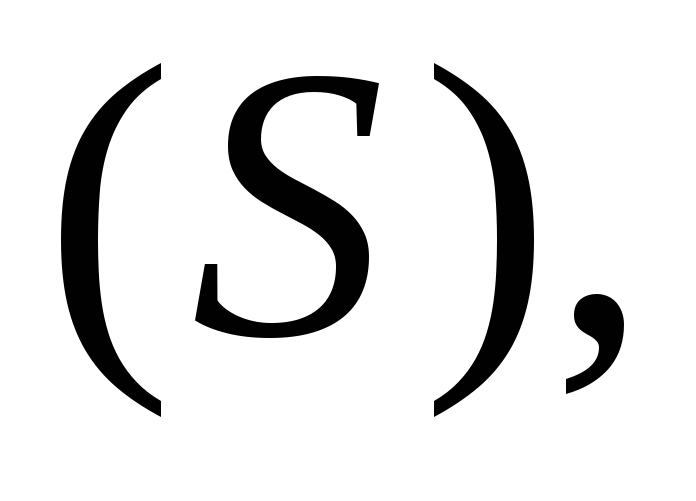 получим массу жидкости, протекающей
сквозь
получим массу жидкости, протекающей
сквозь за единицу времени (массовый расход):
за единицу времени (массовый расход):
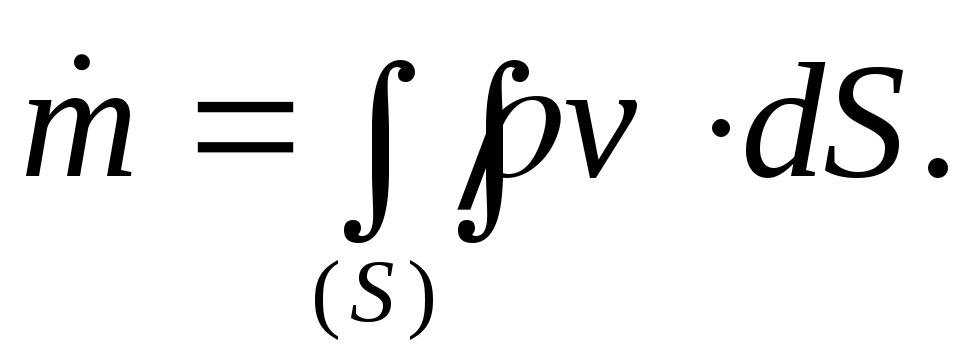
Если поверхность замкнута, то по теореме о дивергенции
(П.4.2) это равенство равносильно такому:
замкнута, то по теореме о дивергенции
(П.4.2) это равенство равносильно такому:
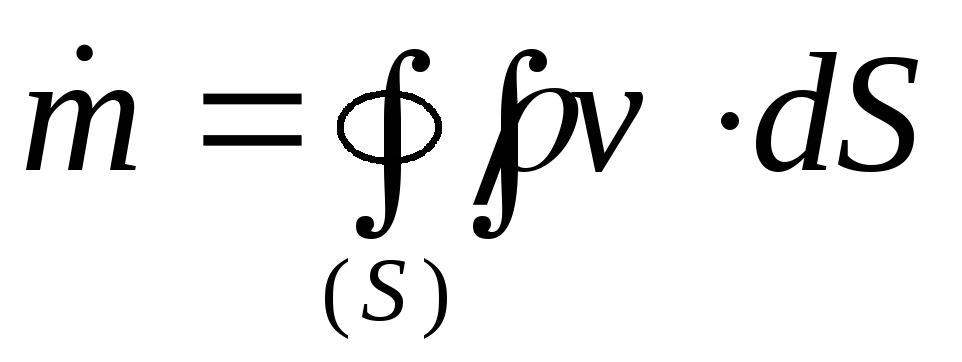
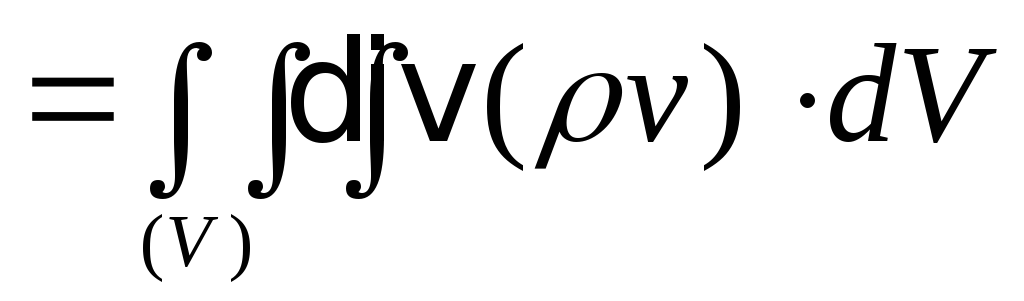 (2.5)
(2.5)
– масса жидкости, вытекающейиз области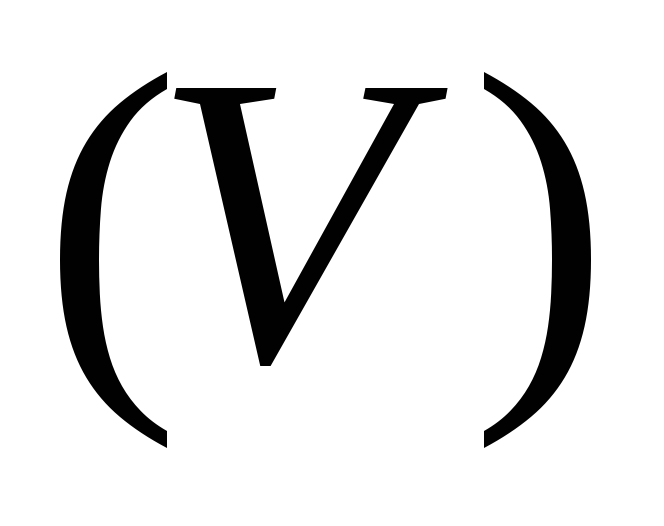 за единицу времени.
за единицу времени.
Пусть область 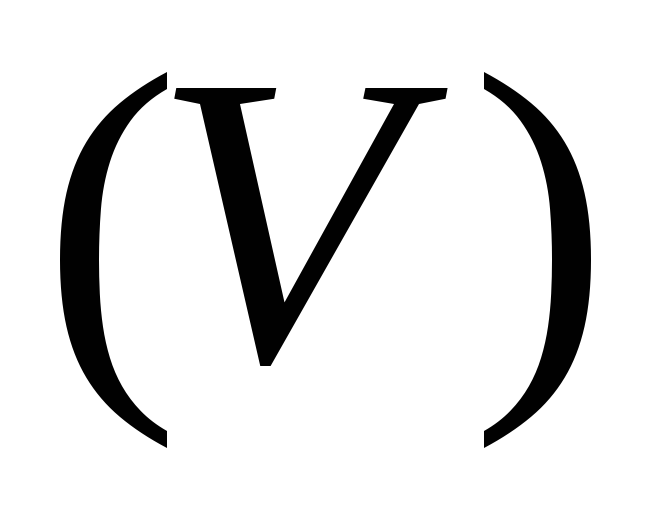 мала; обозначим её
мала; обозначим её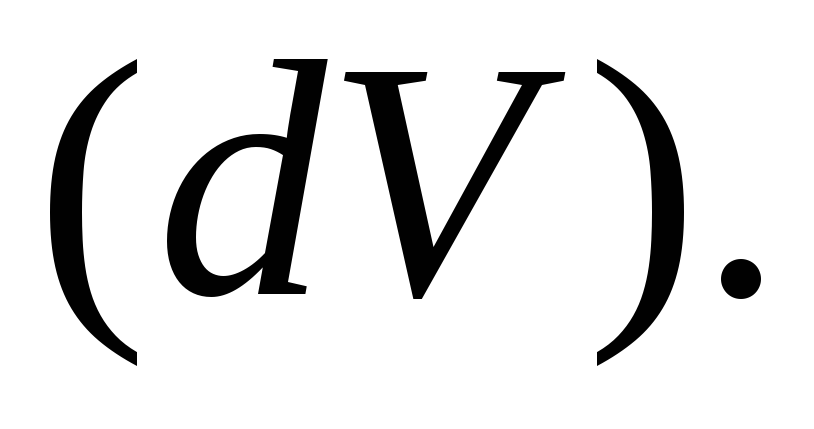 Тогда из (2.5) получим
Тогда из (2.5) получим
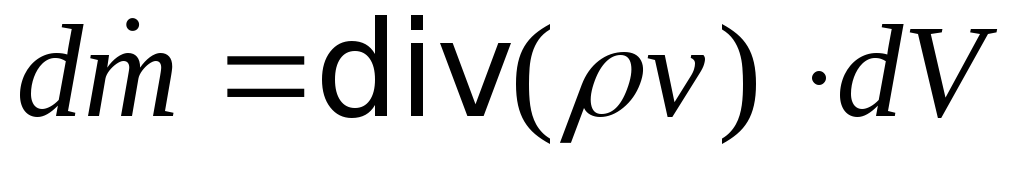 (2.6)
(2.6)
– масса жидкости, вытекающейиз области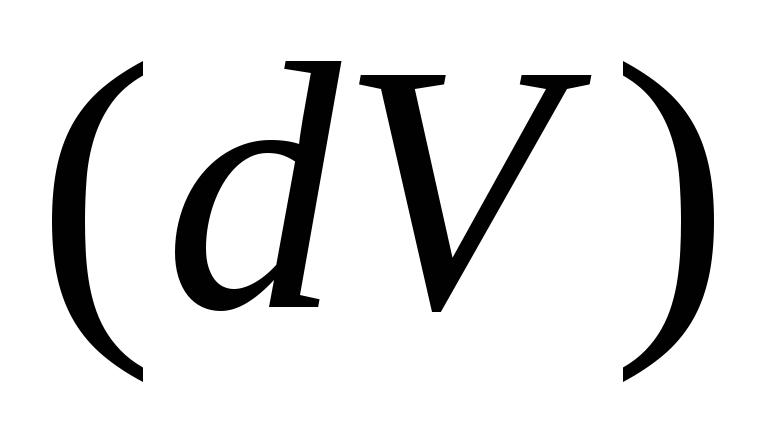 за единицу времени.
за единицу времени.
З а д а ч а 1. Дано поле скоростей текущей жидкости
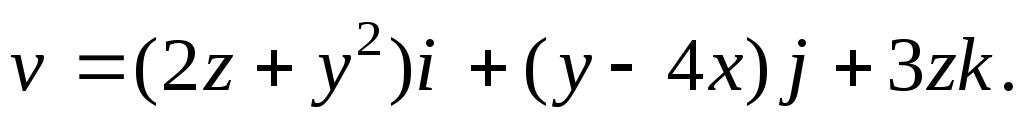
а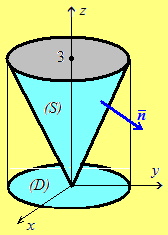 )
Найти расход через боковую поверхность
конуса
)
Найти расход через боковую поверхность
конуса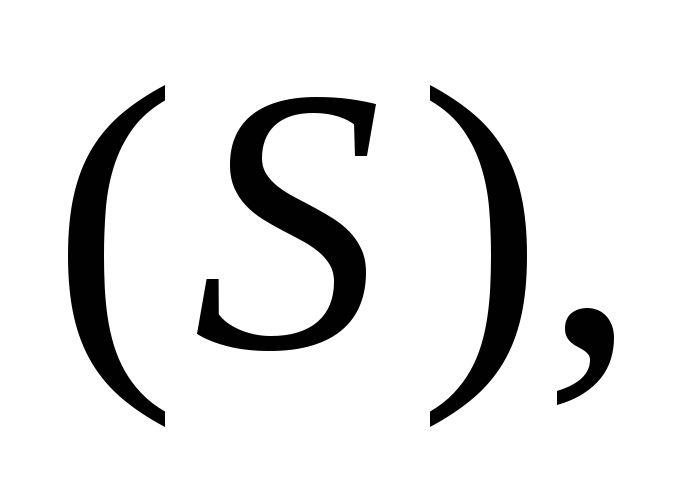 ограниченного заданными поверхностями:
ограниченного заданными поверхностями:
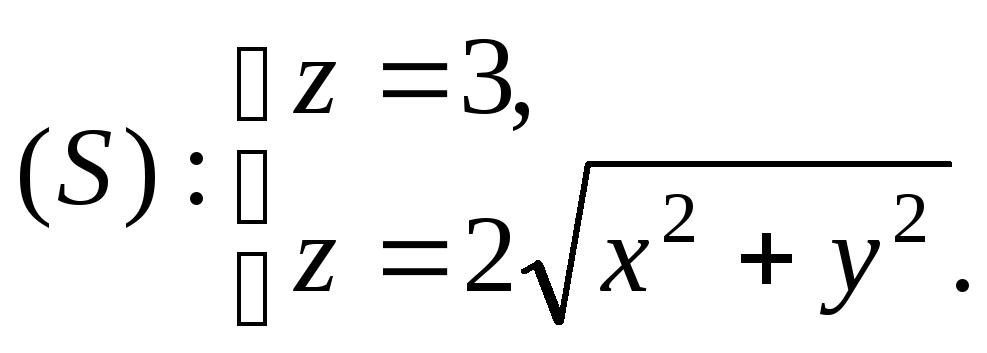 (а)
(а)
б) Найти расход через всю поверхность конуса.
Начертим
конус (рис. 2.6). Равенство 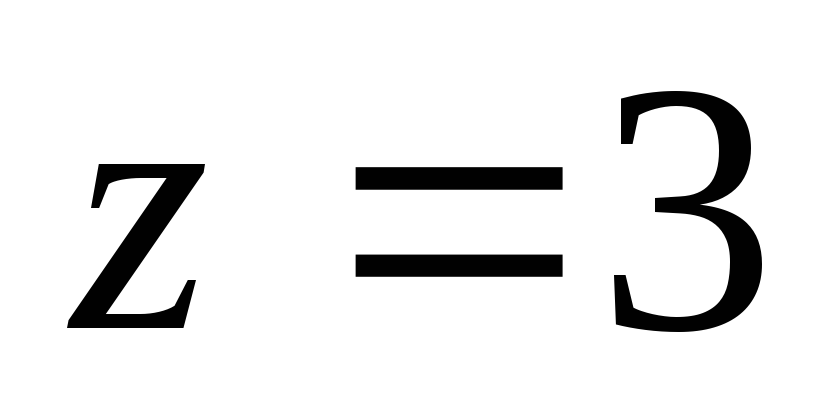 есть уравнение горизонтальной плоскости.
Равенство
есть уравнение горизонтальной плоскости.
Равенство 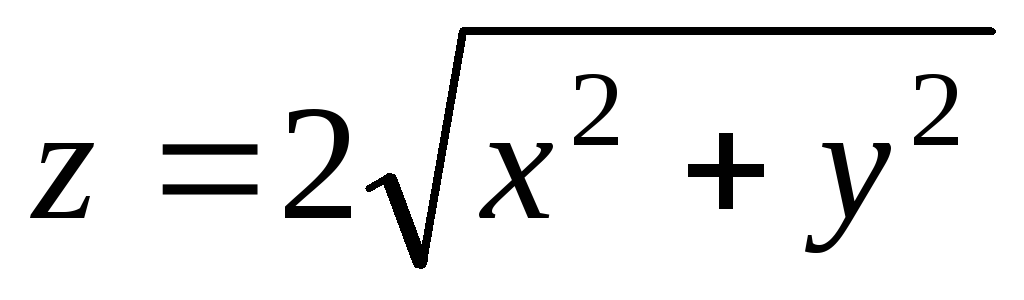 есть уравнение конической поверхности.
есть уравнение конической поверхности.
а) Уравнение конической поверхности запишем так:
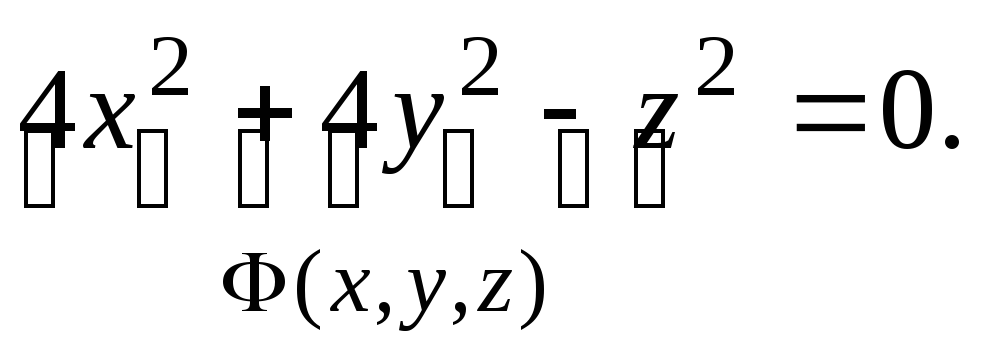
Находим нормальный вектор
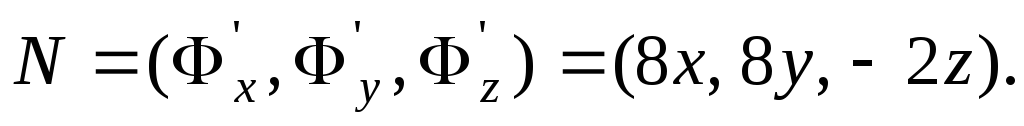 Рис.
2.6
Рис.
2.6
После
сокращения на +2 будем иметь 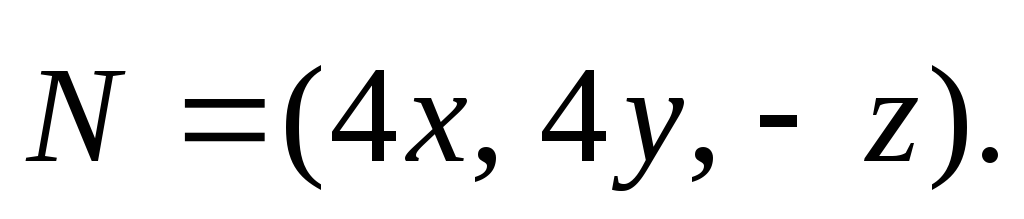
При этом вектор укорачивается, но направление не меняется. Его модуль
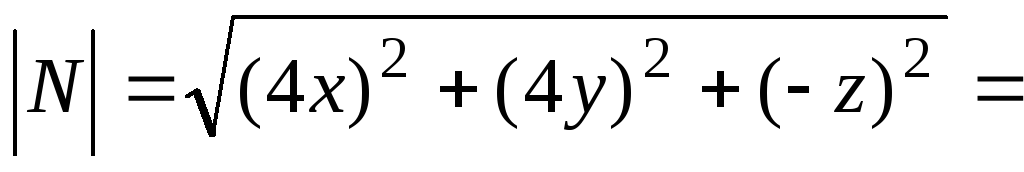
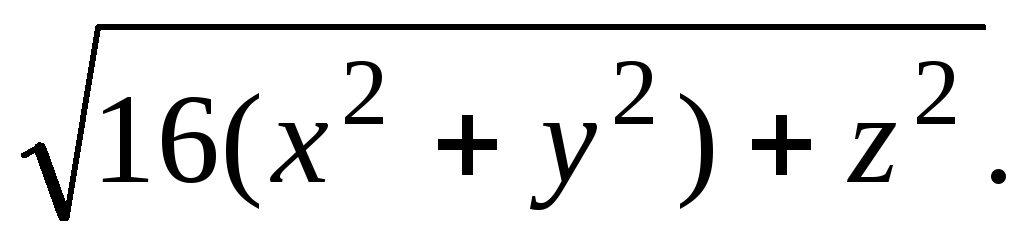
Единичный вектор, нормальный к боковой поверхности конуса, равен
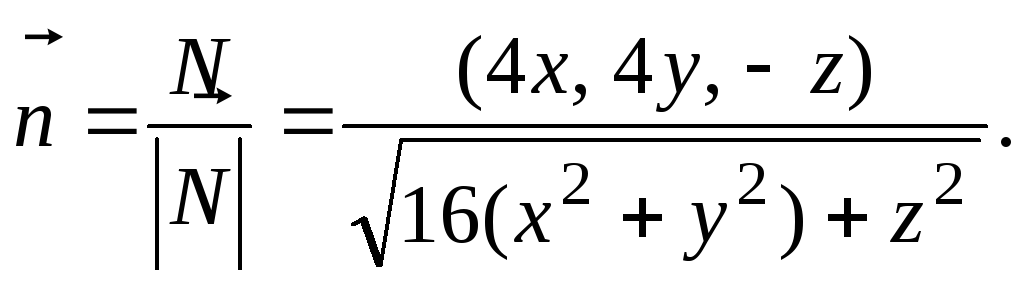
Находим скалярное произведение:
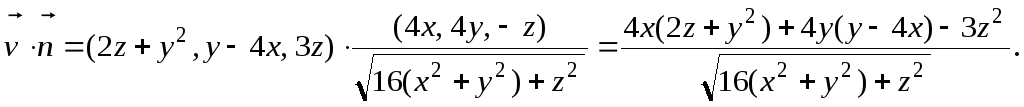
Подставим в формулу расхода (2.2):
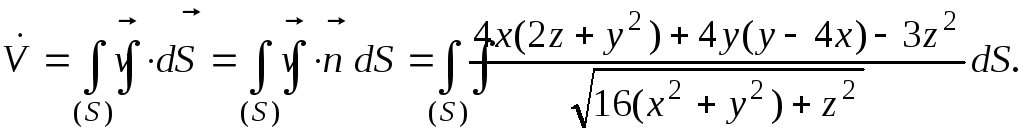
На
поверхности конуса выполняется равенство 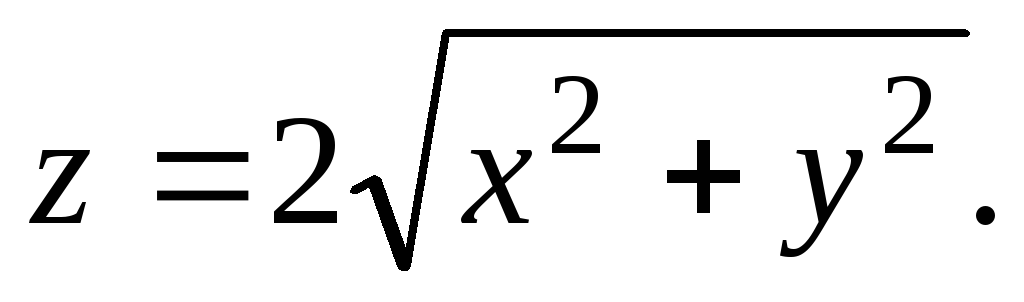 Подставим это
значение:
Подставим это
значение:
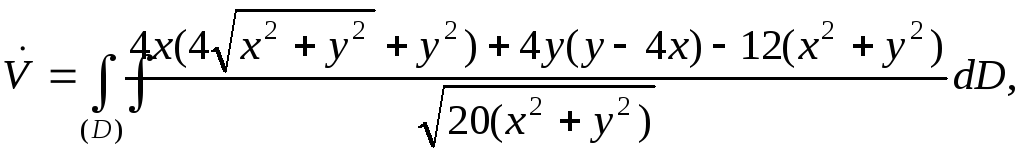
где  круг,проекция
боковой
поверхности конуса
круг,проекция
боковой
поверхности конуса  на плоскость
на плоскость  Из системы уравнений (а) получим
Из системы уравнений (а) получим 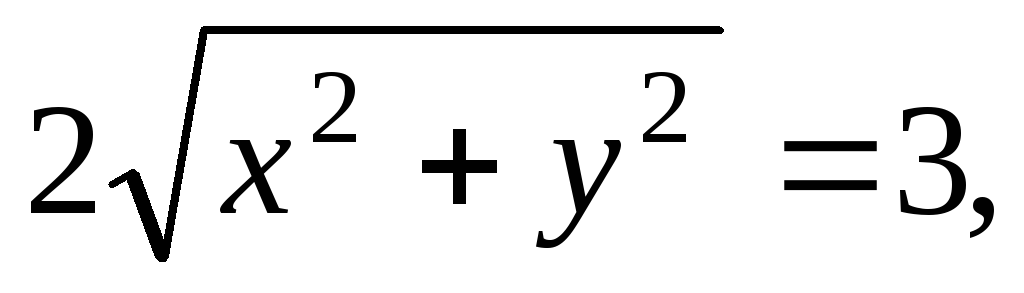 или
или 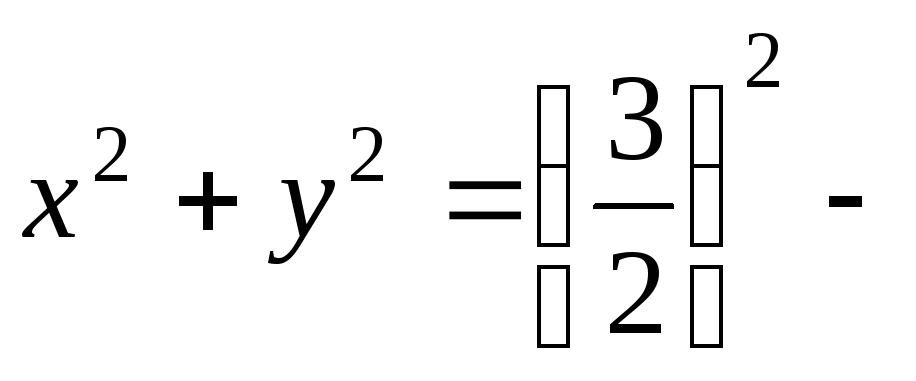 окружность
радиуса
окружность
радиуса 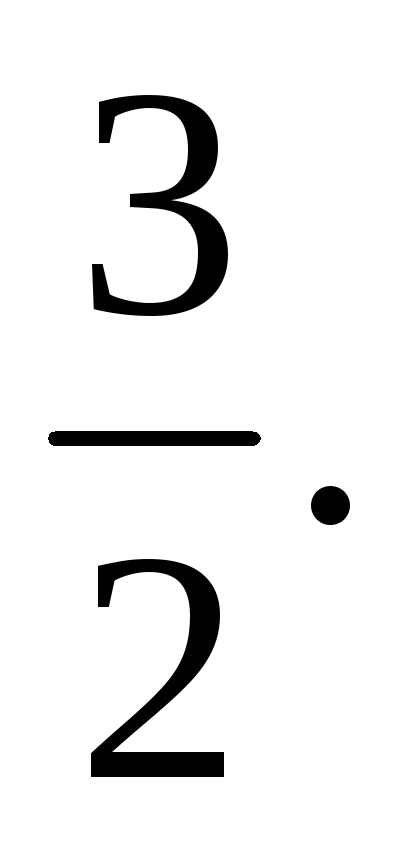
Для
вычисления интеграла перейдём к полярной
системе координат 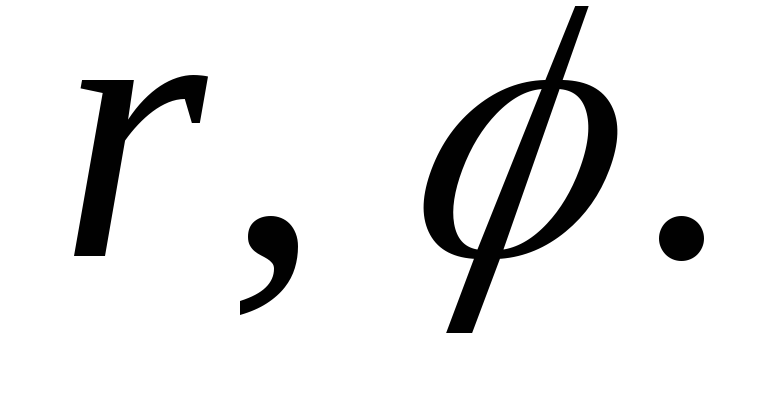 Тогда
Тогда 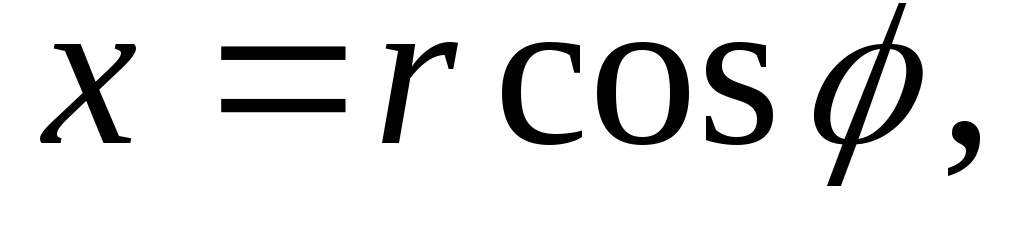
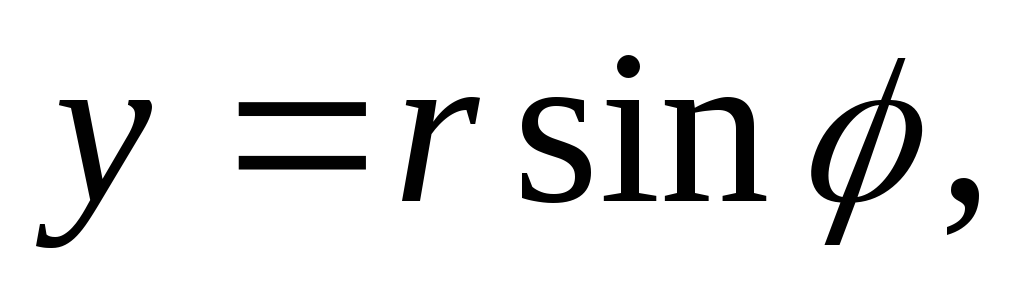
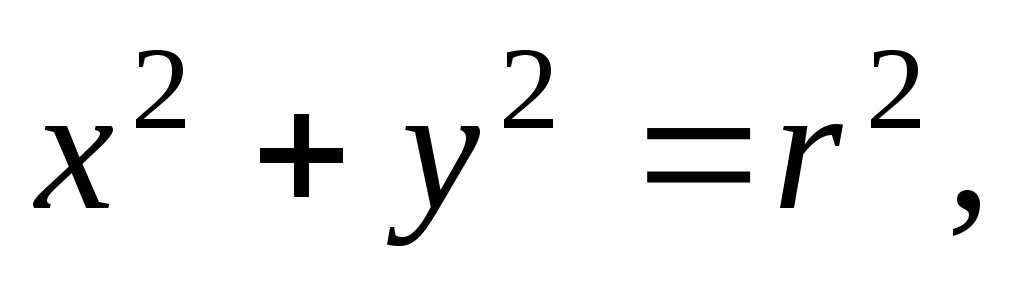
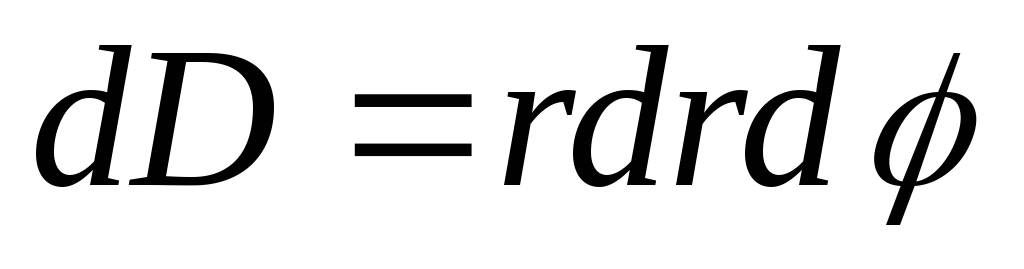 и
и
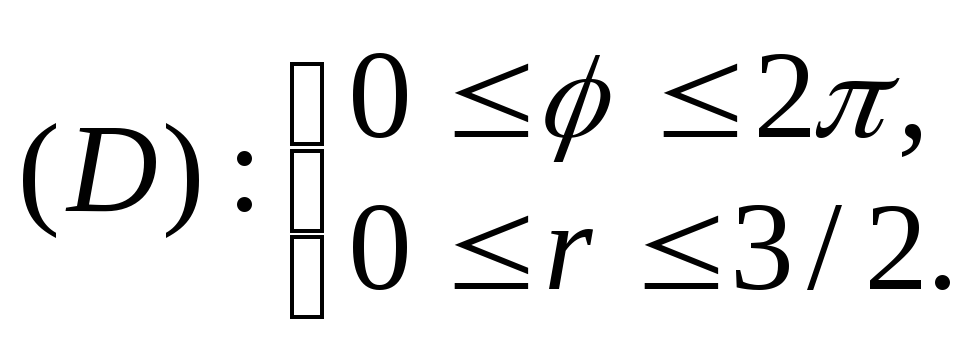
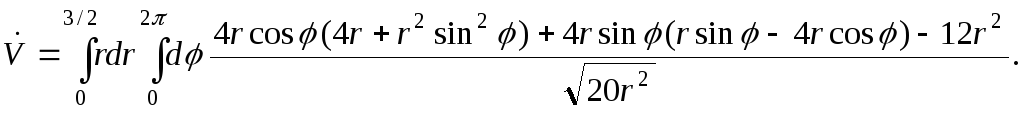
Ввиду того, что
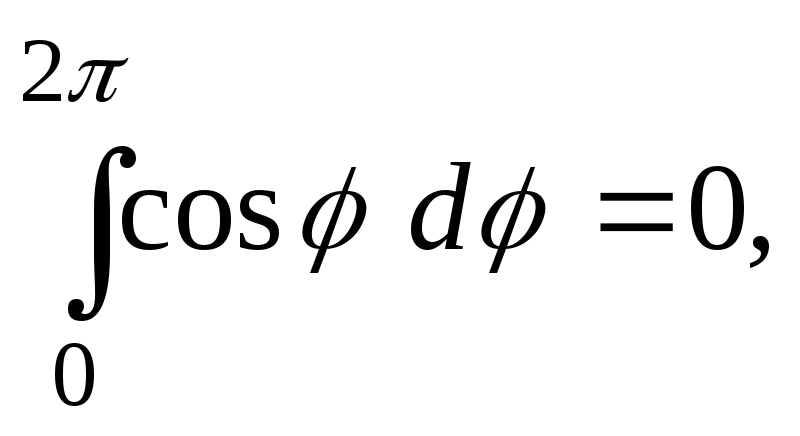
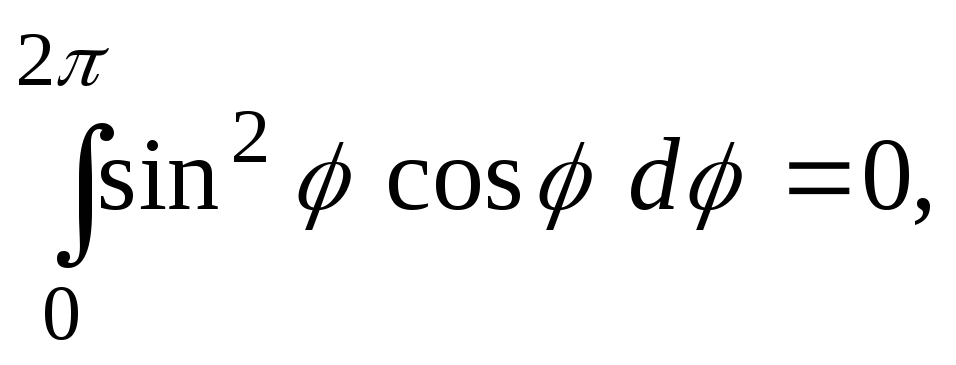
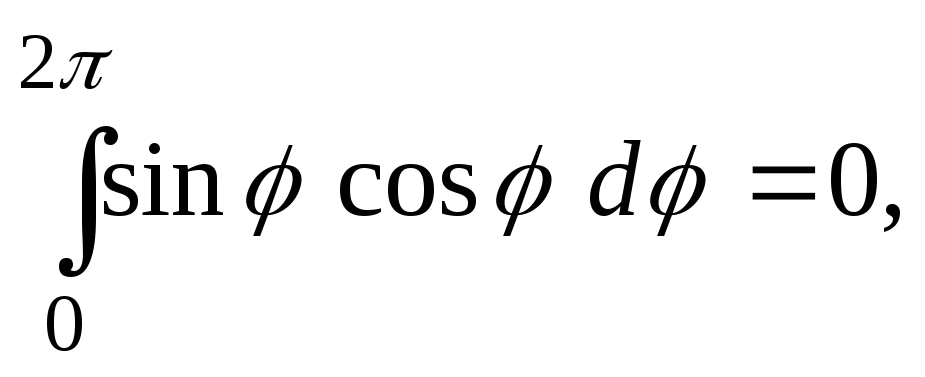
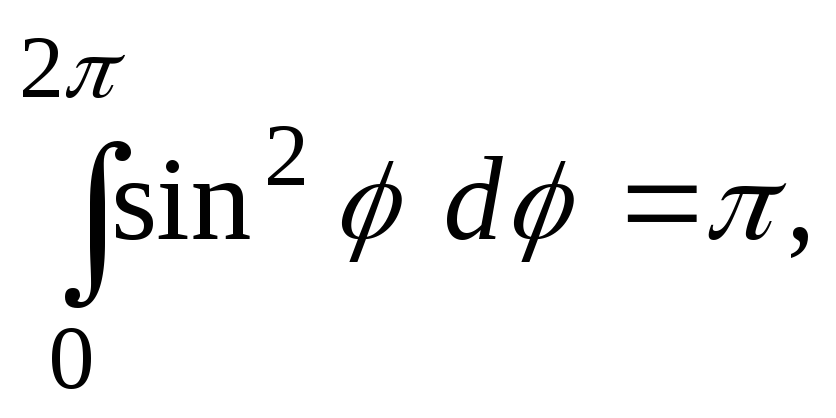
остаётся
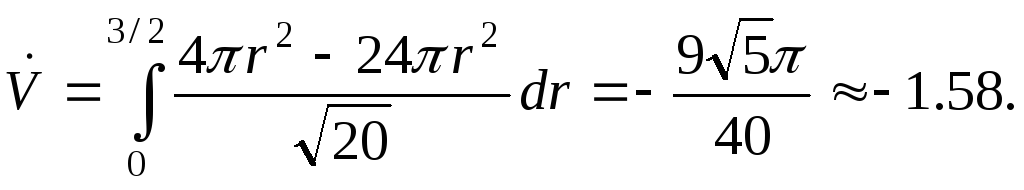
Отрицательность расхода означает, что жидкость в основном втекает через боковую поверхность конуса.
б)
Вся поверхность конуса является замкнутой поверхностью, внутри которой находится
весь конус  поэтому можно воспользоваться формулой
Остроградского-Гаусса. Но сначала найдём
дивергенцию вектора скорости:
поэтому можно воспользоваться формулой
Остроградского-Гаусса. Но сначала найдём
дивергенцию вектора скорости:
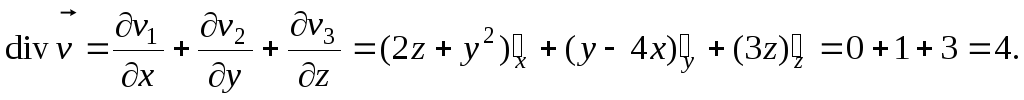
По формуле расхода (2.2) имеем
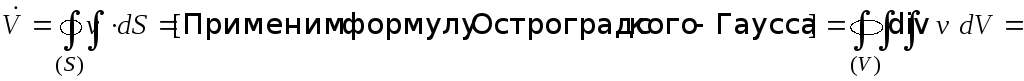
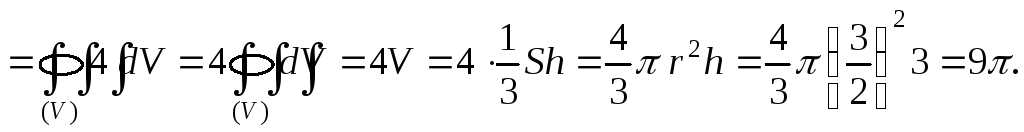
2.4. Расход при стационарном течении.
Течение называют стационарным, когда скорость не зависит от времени.
Рассмотрим течение
жидкости в каком-либо трубопроводе
через поперечные сечения  и
и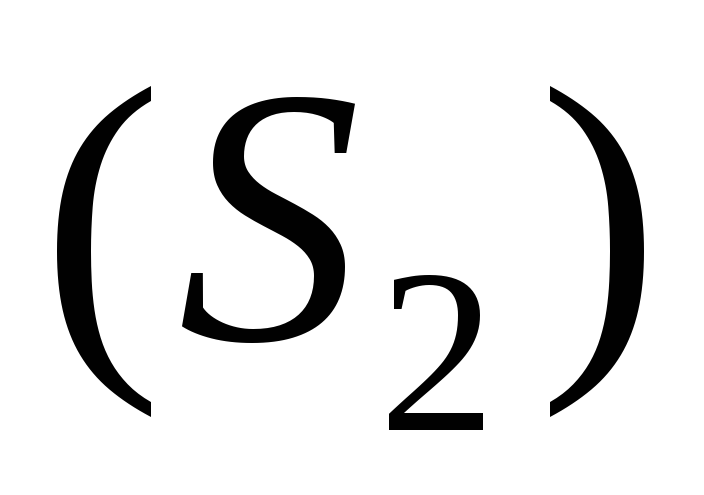 За единицу времени через сечениевтекает объём
За единицу времени через сечениевтекает объём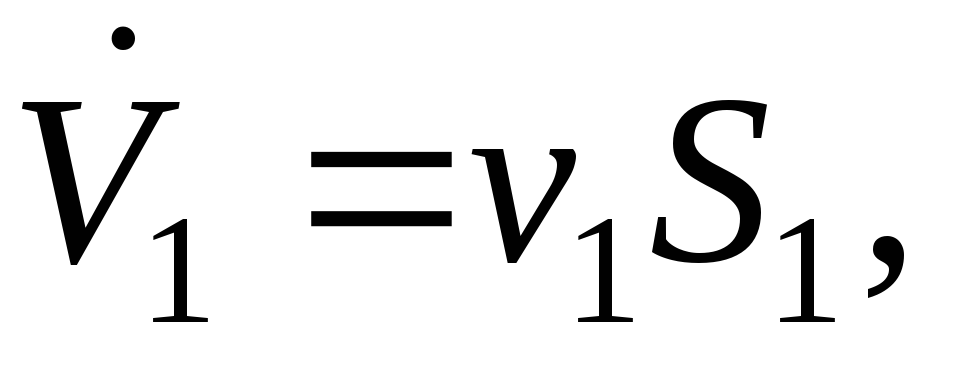 а через
а через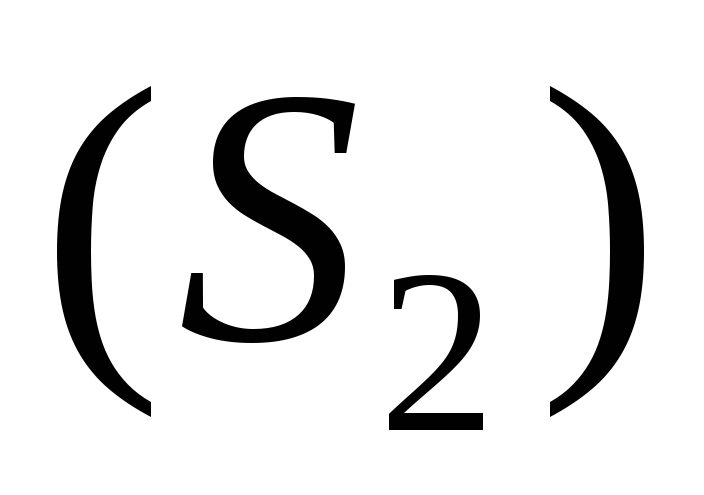 вытекает объём
вытекает объём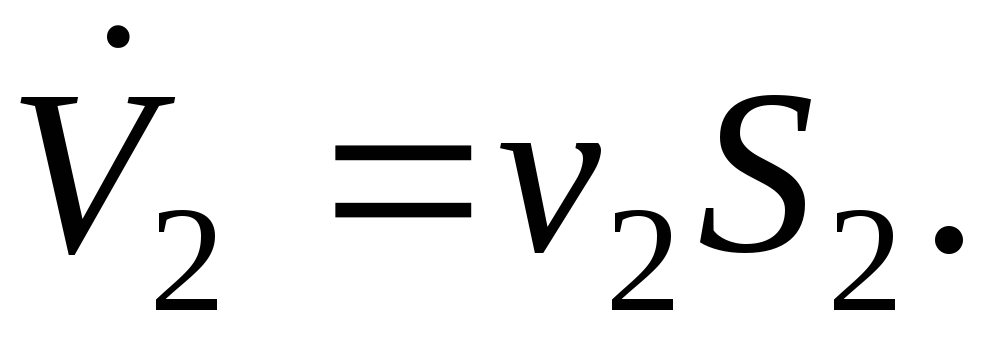 Так как жидкость практически несжимаема,
то в пространстве между
Так как жидкость практически несжимаема,
то в пространстве между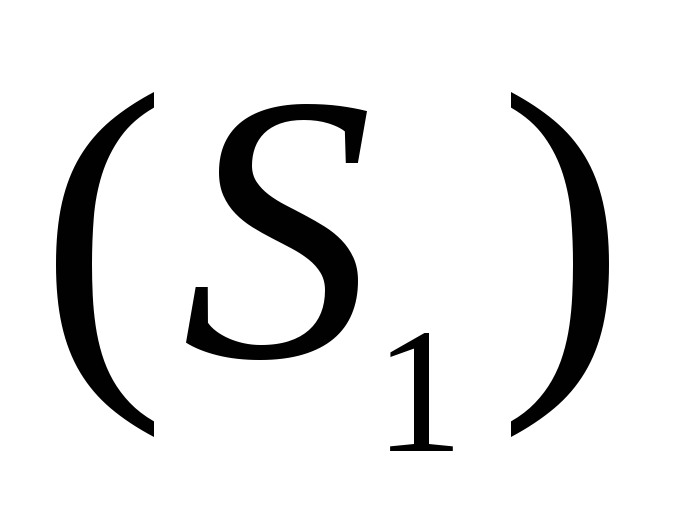 и
и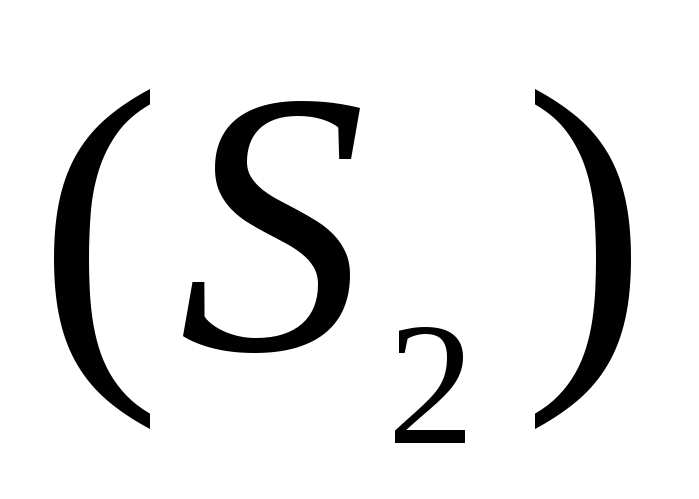 объём жидкости не меняется. Значит,
объём входящей жидкости через сечение
объём жидкости не меняется. Значит,
объём входящей жидкости через сечение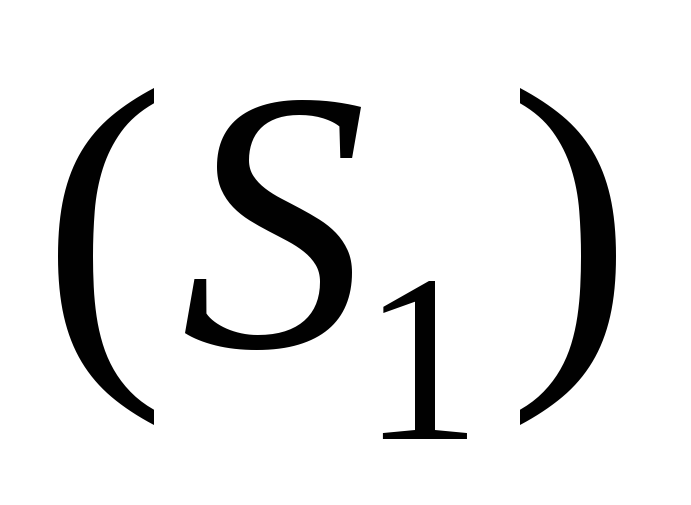 равен объёму выходящей жидкости через
равен объёму выходящей жидкости через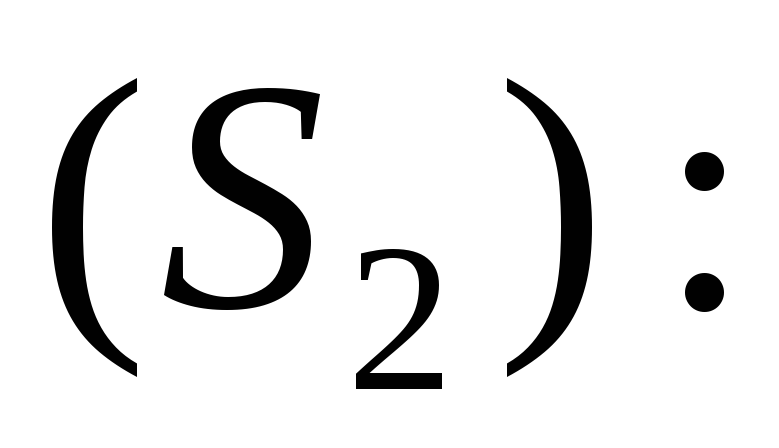
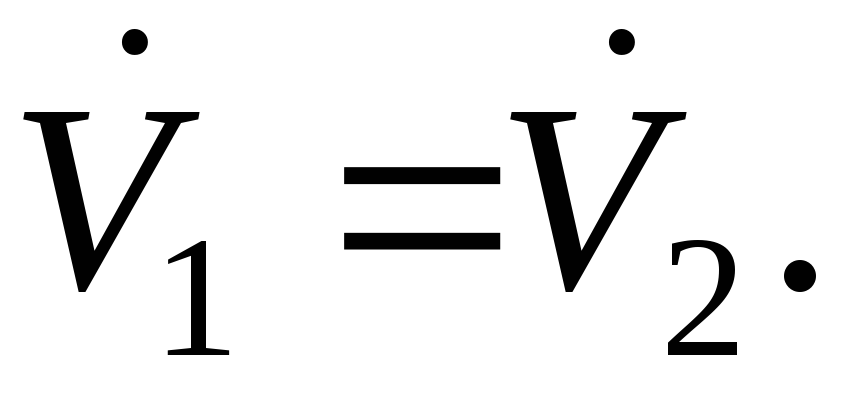 Иначе говоря,
Иначе говоря,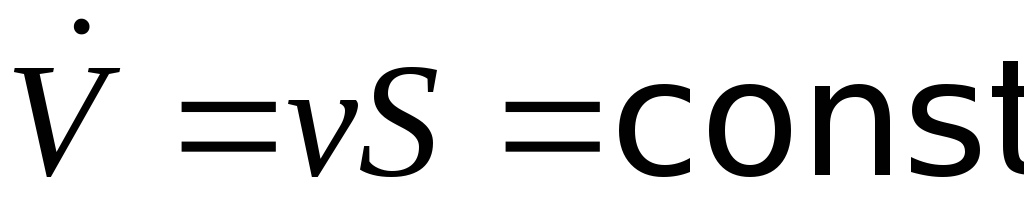 .
Таким образом,
.
Таким образом,
|
Условие постоянства расхода |
(2.7)
Следовательно, там, где сечение больше, скорость меньше.
23. Понятие расхода жидкости, средней скорости, живого сечения, гидравлического радиуса, смоченного периметра.
Живое
сечение (w)
– это поперечное сечение потока,
перпендикулярное ко всем линиям тока.
Например, в круглой трубке диаметром d,
в которой все поперечное сечение занято
жидкостью, живое сечение – это площадь
круга 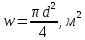
Смоченный
периметр –
та часть периметра живого сечения,
которая соприкасается с твердыми
стенками, образуя смоченную поверхность.
Например, для русла вся боковая поверхность
потока, за исключением свободной
поверхности которую жидкость имеет на
границе с газообразной средой; для
круглой трубы, работающей полным
сечением, смоченный периметр равен
длине окружности, т.е. 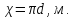
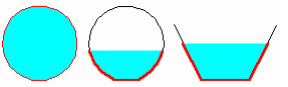
Для круглой незаполненной трубы (рис.), если угол в радианах,
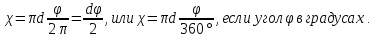
Гидравлический
радиус (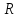 )–
отношение площади живого сечения к
смоченному периметру. Например, для
круглой трубы, работающей полным
сечением, гидравлический радиус четверти
ее диаметра, т. е.
)–
отношение площади живого сечения к
смоченному периметру. Например, для
круглой трубы, работающей полным
сечением, гидравлический радиус четверти
ее диаметра, т. е.
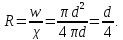
Гидравлический
радиус характеризует удельную, т.е.
приходящуюся на единицу длины смоченного
периметра площадь живого сечения и
позволяет оценить силу трения. Сила
трения жидкости о смоченную поверхность
зависит от ее площади, чем больше
смоченная поверхность, тем больше при
равных условиях сила трения. Расход
жидкости (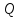 )–
это ее объем, протекающий в единицу
времени через живое сечение потока.
Расход для элементарной струйки
)–
это ее объем, протекающий в единицу
времени через живое сечение потока.
Расход для элементарной струйки 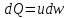 , где
, где 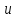 –
истинная скорость движения частиц
жидкости,
–
истинная скорость движения частиц
жидкости, 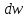 –
площадь сечения элементарной струйки.
Средняя скорость (
–
площадь сечения элементарной струйки.
Средняя скорость (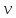 )
– отношение расхода к площади живого
сечения
)
– отношение расхода к площади живого
сечения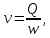 откуда
откуда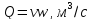 .
.
Расход
– количество жидкоси, которое протекает
через данное сечение в единицу времени.
Различают объёмный Q(м3/с), массовый
Qm(кг/с) и весовой QG (Н/с) расходы. 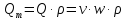 ;
;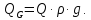

24. Дифференциальное уравнение неразрывности потока.
Выделим
в движущемся потоке элементарный объем
в форме прямоугольного параллелепипеда
(рис.) и определим изменение массы 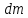 жидкости
в выделенном объеме за элементарный
промежуток времени
жидкости
в выделенном объеме за элементарный
промежуток времени 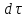 .
Это изменение массы определяется
разностью между втекающей и вытекающей
массой жидкости через грани элементарного
объема. Поскольку объем выделенного
элемента
.
Это изменение массы определяется
разностью между втекающей и вытекающей
массой жидкости через грани элементарного
объема. Поскольку объем выделенного
элемента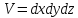 остается
неизменным с течением времени, то
изменение массы жидкости
остается
неизменным с течением времени, то
изменение массы жидкости 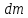 может
быть обусловлено лишь изменением ее
плотности
может
быть обусловлено лишь изменением ее
плотности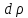 .
. 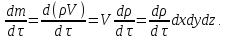
Определим
массу жидкости, втекающую в выделенный
объем за единицу времени. Жидкость
втекает через грани 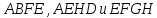 в
следующих количествах: через грань
в
следующих количествах: через грань 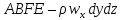 ;
через грань
;
через грань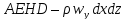 ;
через грань
;
через грань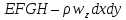 .
.
Жидкость
вытекает через грани 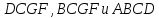 в
следующих количествах: через грань
в
следующих количествах: через грань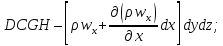 через грань
через грань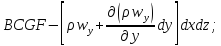 через
грань
через
грань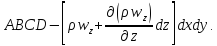
Просуммировав количества втекающей и вытекающей жидкости по всем граням, найдем изменение массы жидкости в выделенном объеме:
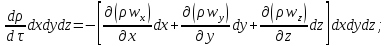
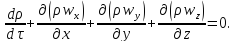
Это
уравнение
называется дифференциальным
уравнением неразрывности или сплошности.
Оно также может быть записано в виде 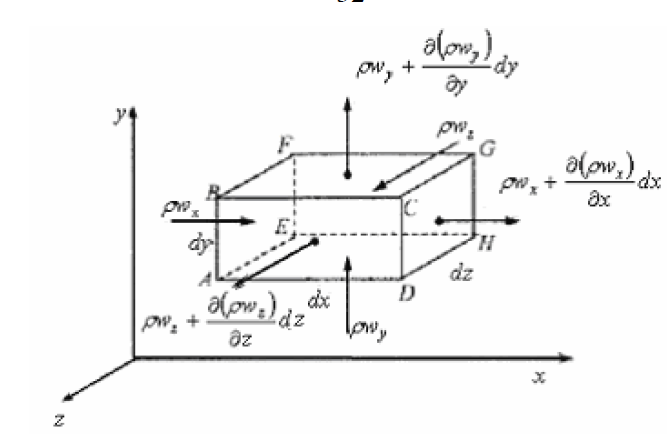
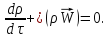 Для
потоков несжимаемой жидкости (стационарных
и нестационарных)
Для
потоков несжимаемой жидкости (стационарных
и нестационарных)
уравнение
неразрывности примет вид 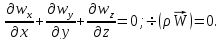 Для
стационарных потоков газа (сжимаемой
жидкости) уравнение неразрывности
примет вид
Для
стационарных потоков газа (сжимаемой
жидкости) уравнение неразрывности
примет вид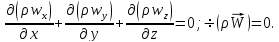 Необходимо
отметить, что существуют и другие способы
вывода уравнения неразрывности.
Необходимо
отметить, что существуют и другие способы
вывода уравнения неразрывности.
Типы потоков жидкости
Совокупность элементарных струек жидкости представляет собой поток жидкости. Различают следующие типы потоков (или типы движений жидкости).
Н апорные
потоки (напорные движения) — это такие, когда поток ограничен
твердыми стенками со всех сторон, при
этом в любой точке потока давление
отличается от атмосферного обычно в
большую сторону, но может быть и меньше
атмосферного. Движение в этом случае
происходит за счёт напора, создаваемого,
например, насосом или водонапорной
башней. Давление вдоль напорного потока
обычно переменное. Такое движение имеет
место во всех гидроприводах технологического
оборудования, водопроводах, отопительных
системах и т.п.
апорные
потоки (напорные движения) — это такие, когда поток ограничен
твердыми стенками со всех сторон, при
этом в любой точке потока давление
отличается от атмосферного обычно в
большую сторону, но может быть и меньше
атмосферного. Движение в этом случае
происходит за счёт напора, создаваемого,
например, насосом или водонапорной
башней. Давление вдоль напорного потока
обычно переменное. Такое движение имеет
место во всех гидроприводах технологического
оборудования, водопроводах, отопительных
системах и т.п.
Б езнапорные
потоки (безнапорные движения) отличаются тем, что поток имеет свободную
поверхность, находящуюся под атмосферным
давлением. Безнапорное движение
происходит под действием сил тяжести
самого потока жидкости. Давление в таких
потоках примерно одинаково и отличается
от атмосферного только за счет глубины
потока. Примером такого движения может
быть течение воды в реке, канале, ручье.
езнапорные
потоки (безнапорные движения) отличаются тем, что поток имеет свободную
поверхность, находящуюся под атмосферным
давлением. Безнапорное движение
происходит под действием сил тяжести
самого потока жидкости. Давление в таких
потоках примерно одинаково и отличается
от атмосферного только за счет глубины
потока. Примером такого движения может
быть течение воды в реке, канале, ручье.
С вободная
струяне
имеет твёрдых стенок. Движение происходит
под действием сил инерции и веса жидкости.
Давление в таком потоке практически
равно атмосферному. Пример свободной
струи – вытекание жидкости из шланга,
крана и т.п.
вободная
струяне
имеет твёрдых стенок. Движение происходит
под действием сил инерции и веса жидкости.
Давление в таком потоке практически
равно атмосферному. Пример свободной
струи – вытекание жидкости из шланга,
крана и т.п.
Гидравлические характеристики потока жидкости
В гидравлике различают следующие характеристики потока: живое сечение, смоченный периметр, гидравлический радиус, расход, средняя скорость.
Живым сечением потока называется поверхность (поперечное сечение), нормальная ко всем линиям тока, его пересекающим, и лежащая внутри потока жидкости. Площадь живого сечения обозначается буквой ω. Для элементарной струйки жидкости используют понятие живого сечения элементарной струйки (сечение струйки, перпендикулярное линиям тока), площадь которого обозначают через dω.
Смоченный периметр потока – линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. Длина этой линии обозначается буквой .
В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками.
Гидравлическим радиусом R потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения S к смоченному периметру :
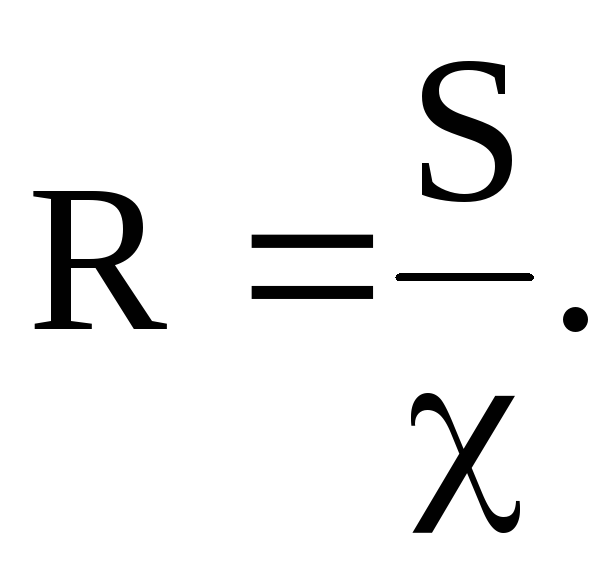
При напорном движении в трубе круглого сечения гидравлический радиус будет равен:
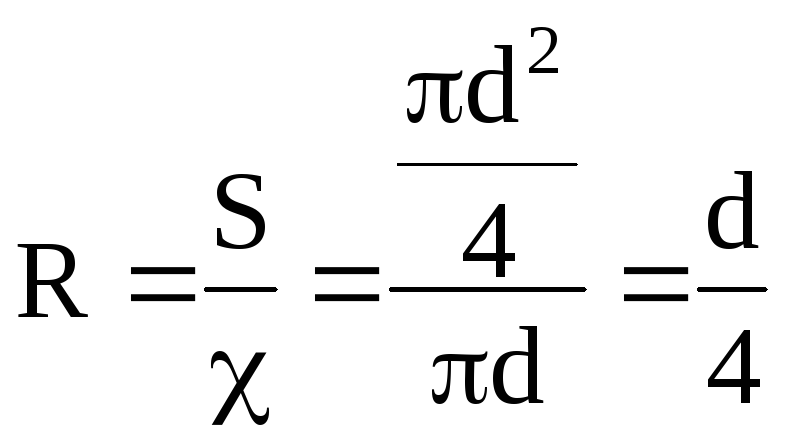
 ,
,
т.е. четверти диаметра, или половине радиуса трубы.
Для безнапорного
потока прямоугольного сечения с размерами 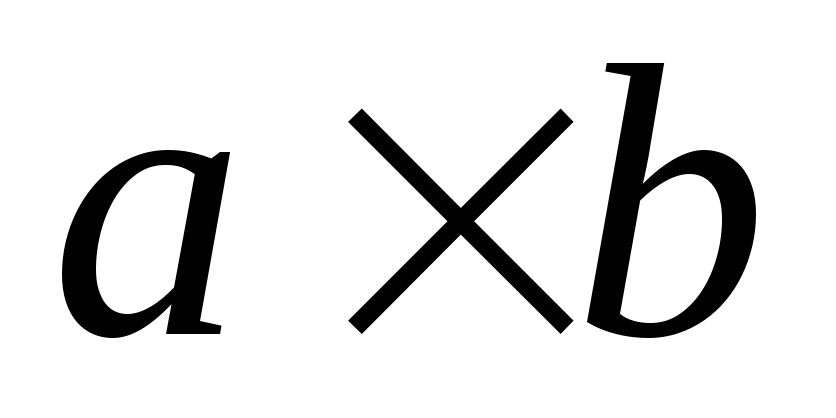 гидравлический
радиус можно вычислить по формуле
гидравлический
радиус можно вычислить по формуле
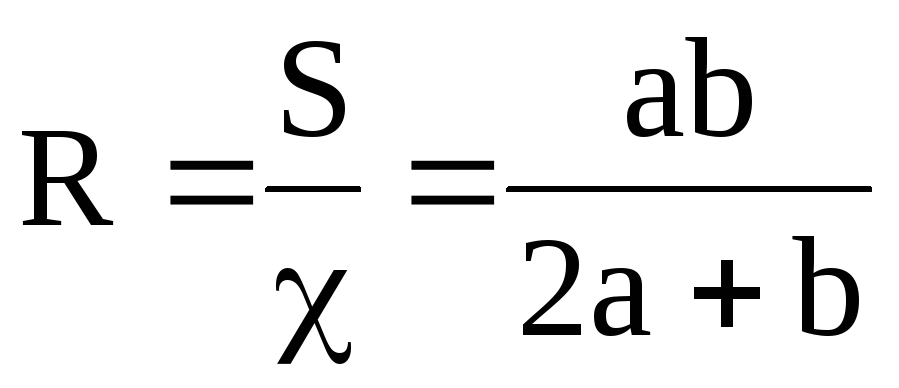
 .
.
Свободная поверхность жидкости при определении смоченного периметра не учитывается.
Расход потока жидкости (расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока.
Различают объёмный, массовый и весовой расходы жидкости.
Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, дм3/с или л/с. Он вычисляется по формуле
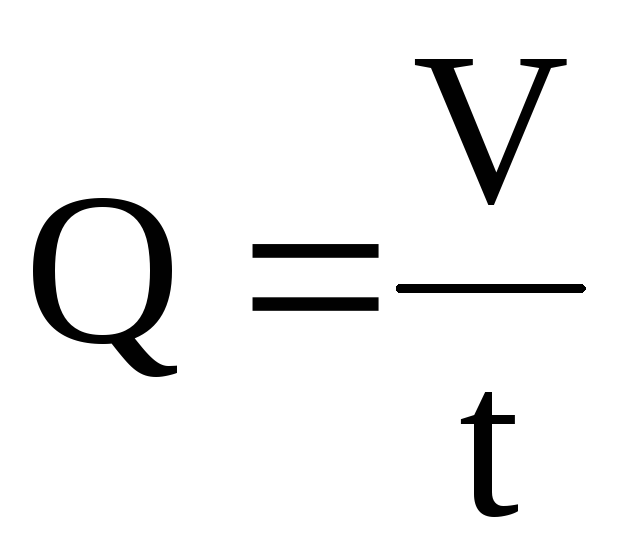 ,
,
где Q — объёмный расход жидкости,
V — объём жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле
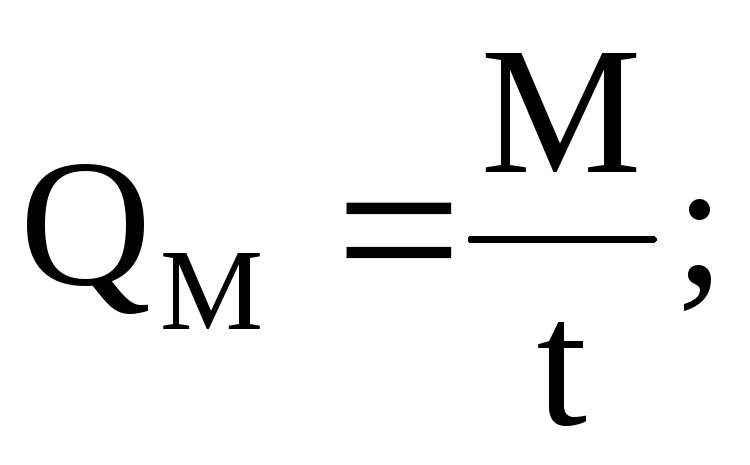
где QM — массовый расход жидкости,
M — масса жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так:
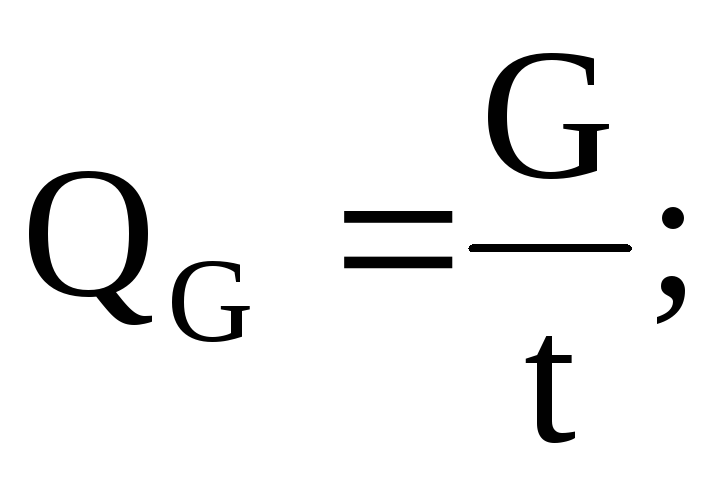
где QG — весовой расход жидкости,
G — вес жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.
Расход элементарной струйки – объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Таким образом:
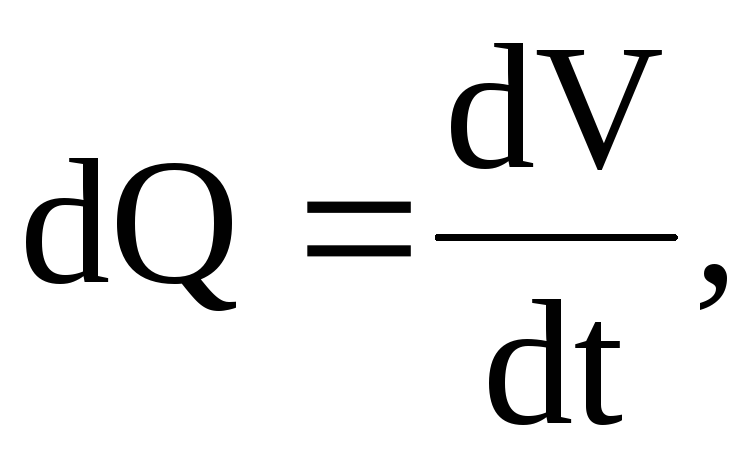
Если последнее выражение проинтегрировать по площади живого сечения потока можно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек
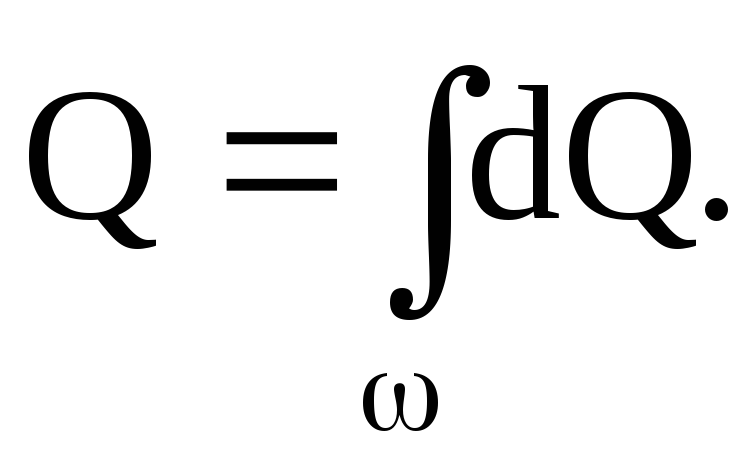
Применение этой формулы в расчетах весьма затруднительно, так как расходы элементарных струек жидкости в различных точках живого сечения потока различны. Поэтому в практике для определения расхода чаще пользуются понятием средней скорости потока.
Средняя скорость потока жидкости Vср в данном сечении это не существующая в действительности скорость потока, одинаковая для всех точек данного живого сечения, с которой должна была бы двигаться жидкость, что бы её расход был равен фактическому.
15) Элементарная струйка, поток жидкости, живое сечение. Гидравлический радиус, расход и средняя скорость.
Часть потока, заключенная внутри трубки тока, называется элементарной струйкой. Поток Ж – представляет собой совокупность элементарных струек.
Живым сечением – сечение потока Ж, перпендикулярное направлению скорости ее сечения. При плавно изменяющемся движении Ж сечение считается плоским и равным площади поперечного сечения потока ().
Площадь живого сечения S= dS
Расход
потока Q
— объем жидкости V,
протекающей за единицу времени t
через живое сечение ω. 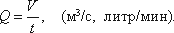
Средняя
скорость потока υ
— скорость движения жидкости, определяющаяся
отношением расхода жидкости Q
к площади живого сечения ω 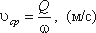
Гидравлический
радиус потока R
— отношение живого сечения к смоченному
периметру 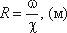 Смоченный
периметр χ
(«хи») — часть периметра живого
сечения, ограниченное твердыми стенками.
Смоченный
периметр χ
(«хи») — часть периметра живого
сечения, ограниченное твердыми стенками.
16) Уравнение неразрывности. Понятие расхода.
Течение жидкости
называют стационарным,
если в каждой точке пространства,
занимаемого жидкостью, ее скорость с
течением времени не изменяется.Жидкости
практически несжимаемы,
т. е. можно считать, что данная масса
жидкости всегда имеет неизменный объем.
Поэтому одинаковость объемов жидкости,
проходящих через разные сечения трубы,
означает, что скорость течения жидкости
зависит от сечения трубы. Пусть скорости
стационарного течения жидкости через
сечения трубы S1 и S2 равны соответственно v1 и v2.
Объем жидкости, протекающей за промежуток
времени t через сечение S1,
равен V1=S1v1t,
а объем жидкости, протекающей за то же
время через сечение S2, равен V2=S2v2t.
Из равенства V1=V2 следует, что 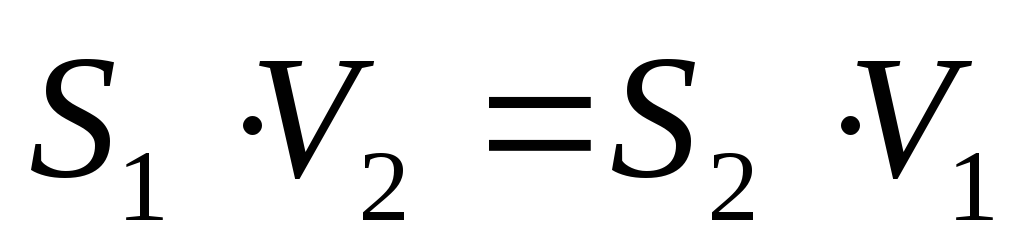 уравнением
неразрывности.
Из него следует, что
уравнением
неразрывности.
Из него следует, что 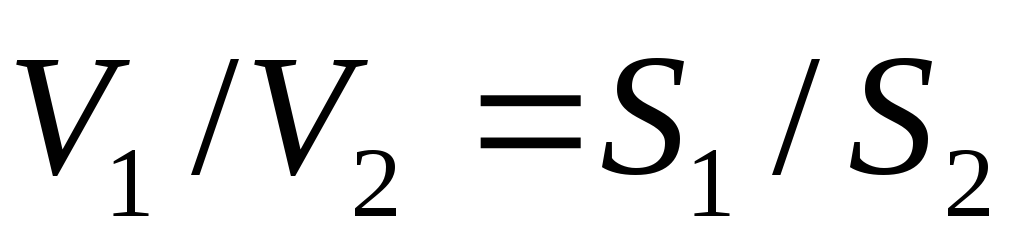 Следовательно, при стационарном течении
жидкости скорости движения ее частиц
через разные поперечные сечения трубы
обратно пропорциональны площадям этих
сечений.
Следовательно, при стационарном течении
жидкости скорости движения ее частиц
через разные поперечные сечения трубы
обратно пропорциональны площадям этих
сечений.
Расходом называется количество жидкости, протекающее через живое течение потока (струйки) в единицу времени. Различают объёмный Q (м3/с), весовой QG(Н/с) и массовый Qm(кг/с) расходы.
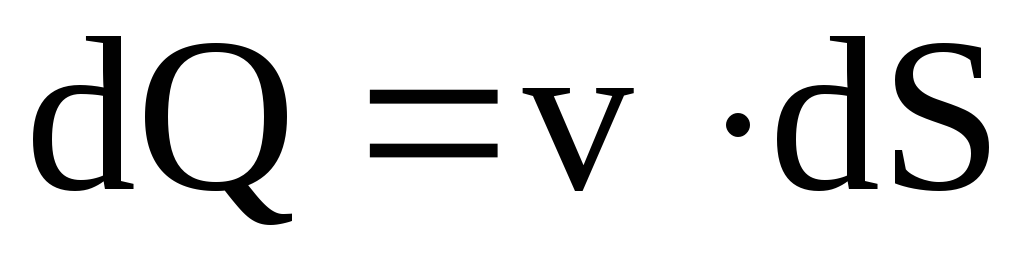 ;
; 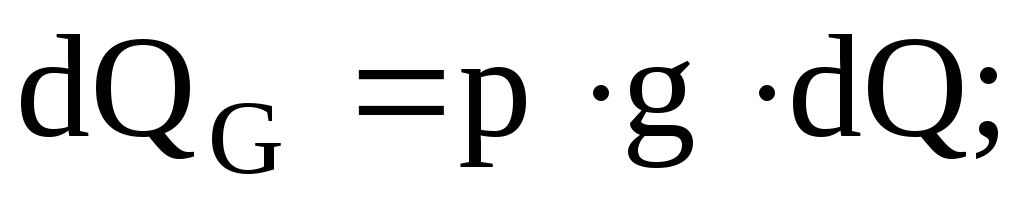
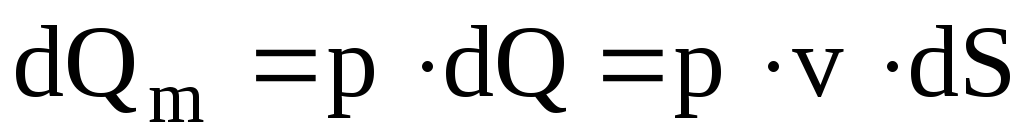
17) Распределение сил в сплошной среде. Объемные и поверхностные силы.
Внешние силы: массовые (объемные) и поверхностные.
Массовые силы в соответствии со вторым законом Ньютона пропорциональны массе жидкости или, для однородной жидкости, — ее объему. К ним относятся сила тяжести и сила инерции переносного движения.
Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности.
Массовые силы относят к единице массы, а поверхностные к единице площади
Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей.
Если плотность сплошной среды постулируется равной константе, то такая сплошная среда называется несжимаемой.
18) Уравнение Бернулли для установившегося движения жидкости.
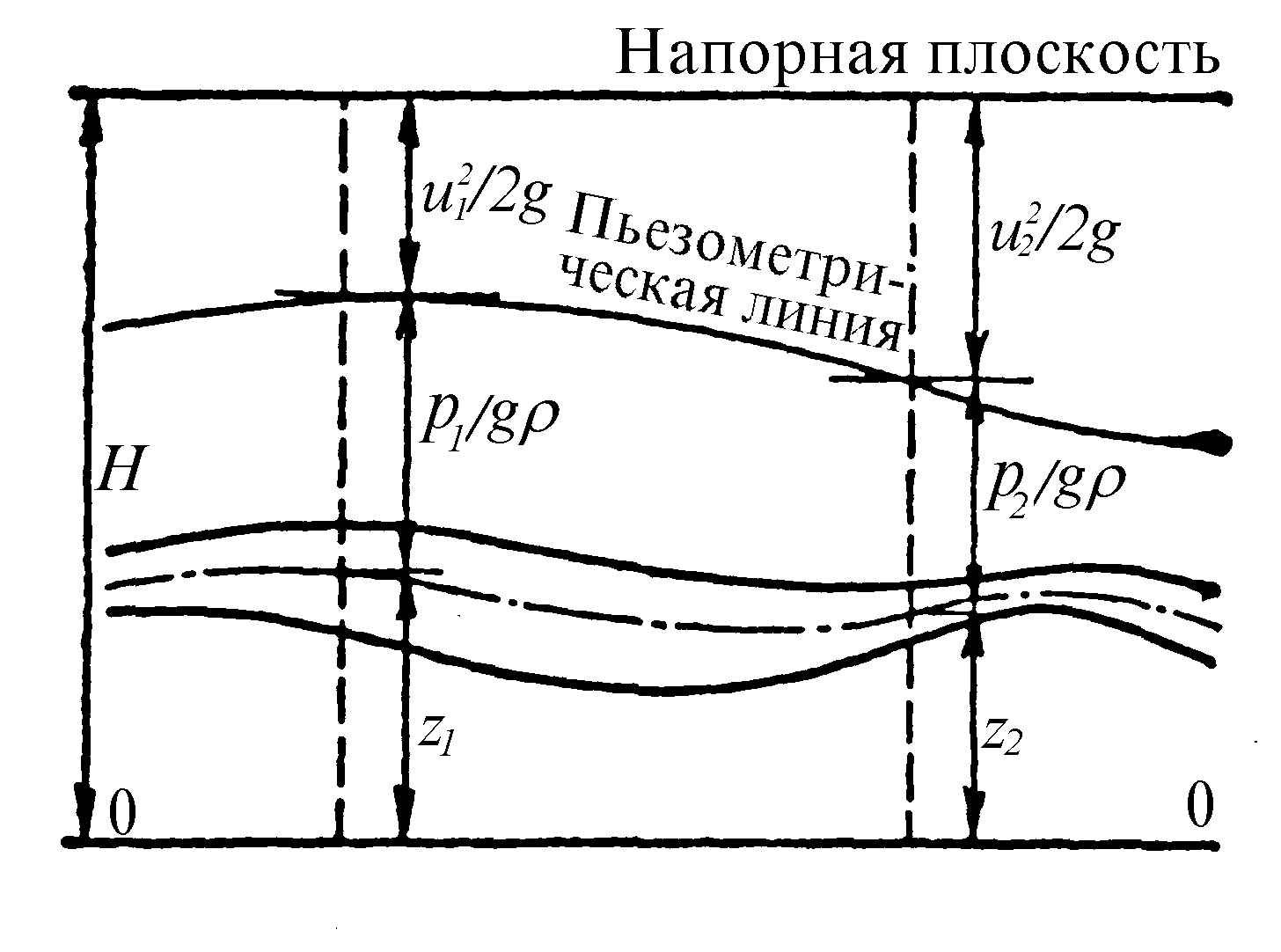
Напорная линия – линия показывающая изменение гидродинамического напора Ж по длине потока
Линия, соединяющая уровни Ж в пьезометрах наз-ся пьезометрической линией
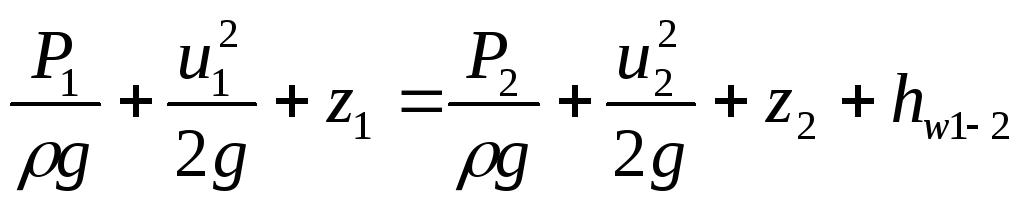
Отметим, что в такой записи члены уравнения выражают удельную энергию, отнесенную к весу (Mg = G).
Как и в гидростатике, величину z называют высотой положения, а величину p/gρ — пьезометрической высотой.
Сумма первых двух членов уравнения z + p/gρ — пьезометрический напор.
Третий член уравнения u2/2g линейная величина. Как известно, начавшаяся двигаться вертикально со скоростью u при отсутствии сопротивления движению, поднялась бы на высоту u2/2g. Этот член уравнения Бернулли называется скоростной высотой или скоростным напором.
Поток жидкости и его параметры
Поток жидкости — это часть неразрывно движущейся жидкости, ограниченная твердыми деформируемыми или недеформируемыми стенками, образующими русло потока. Потоки, имеющие свободную поверхность, называются безнапорными. Потоки, не имеющие свободной поверхности, называются напорными
Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.
Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.
Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.
Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Рис. Векторы скорости потока жидкости (а) и живое сечение потока (б)
Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.
Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.
Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.
Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).

Рис. Распределение скоростей движения жидкости в живом сечении трубы при течении: а — турбулентном; б — ламинарном
Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:
Vcр = Sэ/d,
где Sэ — площадь эпюры местных скоростей; d — диаметр трубы
Объемный расход жидкости рассчитывается по формуле:
Q = Sэ*Мср,
где Q — площадь живого сечения потока.
Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.
Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.
Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.
Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.
Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.
Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.
Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.
Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.
Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.
Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.
Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:
Re = vd/V,
где Re — число Рейнольдса; v — средняя скорость потока; d — диаметр трубопровода; V — кинематическая вязкость жидкости.
Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.
Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re < 2320 движение жидкости — ламинарное, а при Re > 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:
vкр = 2320v/d