Сложные проценты — восьмое чудо света!
На чтение 4 мин. Обновлено
Основатель династии Ротшильдов, самый богатый человек в мире для своего времени считал сложный процент восьмым чудом света. А он знал, о чем говорит. Сегодня семейство Ротшильдов владеет состоянием в 3 триллиона долларов. Сумма вложенных под сложные проценты денег начинает увеличиваться просто геометрическими темпами.
Сложный процент – что это? Не будем вдаваться в точные определения, по простому — это начисления процентов на начисленные проценты. И с каждым расчетным периодом эти начисленные проценты все больше и больше. Деньги нарастают как снежный ком.
Для примера: вы вложили в банк $1 000 под 10% годовых. Через год ваш вклад составить 1 100 долларов, то есть вам были начислены проценты в размере $100. На второй год ваша сумма в банке составит не $1200, а $1210 ($1100 + 10%). Через 3 – 1 331$, ну и так далее.
Конечно – это не очень впечатляющие цифры, гораздо больший эффект наблюдается по истечении длительного периода времени исчисляемого десятилетиями. Но, тем не менее, при низких первоначальных вложениях капитал можно нарастить весьма значительный.
Но, тем не менее, при низких первоначальных вложениях капитал можно нарастить весьма значительный.
Результаты от сложных процентов на исторических примерах
Деньги Франклина.
Бенджамин Франклин (портрет на 100 долларовой купюре) после свой смерти завещал по 1 000 фунтов (примерно 2 тыс. долларов) на благотворительность двум городам – Бостону (где он родился) и Филадельфии (где он вырос). Единственным условие было не тратить эти деньги в течение 200 лет. Трасты, которым достались эти деньги в управление, вкладывали их в различные предприятия под различные проценты.
Итог: к 1990 году Бостон имел 5 млн. долларов на счету «франклинских» денег, Филадельфия – около 2 млн.
Остров Манхеттен
Эту историю любят приводит в пример преподаватели экономики в американских университетах, как пример чуда сложных процентов. В далеком 1626 году колонисты приобрели у тогдашних коренных жителей остров Манхеттен за $24. В пересчете на сегодняшний эквивалент что-то около $1000. Индейцы деньги благополучно потратили и забыли. Конечно, они же не знали про реинвестирование капитала. Дикари! А теперь внимание!!! Если бы они вложили эти деньги хотя бы под 10% годовых, к сегодняшнему дню смогли выкупить остров Манхеттен обратно, причем со всеми его постройками (небоскребами, дорогами, метро и магазинами). В их собственности набежала бы сумма, превышающая 200 триллионов долларов.
В пересчете на сегодняшний эквивалент что-то около $1000. Индейцы деньги благополучно потратили и забыли. Конечно, они же не знали про реинвестирование капитала. Дикари! А теперь внимание!!! Если бы они вложили эти деньги хотя бы под 10% годовых, к сегодняшнему дню смогли выкупить остров Манхеттен обратно, причем со всеми его постройками (небоскребами, дорогами, метро и магазинами). В их собственности набежала бы сумма, превышающая 200 триллионов долларов.
Золотая монета
Одна притча гласить, что один богач пожертвовал Иисусу золотую монету. И еще остался виноват. Но речь не об этом. Если бы он инвестировал ее под проценты, только с условием, что проценты также начислялись ему золотом под 6% годовых. Как вы думаете – сколько золота у него было бы? Тонна? Две? Десять? Может быть 100 тонн золота?
Одна золотая монета за 2 тысячи лет превратилась бы в огромный шар по весу приблизительно равный весу Земли!!!!!
Полученные результаты конечно впечатляют! Но чтобы их получить никто же не будет ждать так долго. Давайте посмотрим, что мы можем достичь за более короткий срок.
Давайте посмотрим, что мы можем достичь за более короткий срок.
Допустим, вы хотите достичь капитала, позволяющего получать вам доход в виде начислений процентов равных вашему сегодняшнего доходу.
Для простоты расчета возьмем текущий ваш доход в $1000 ежемесячно. Ежемесячно будет инвестировать 10% от ваших заработков (т.е. 100$) под 20% годовых.
Получаются следующие результаты:
Срок Вложено Конечная Сумма
1 год 1200 1380
5 лет 6000 9300
10 лет 12000 28000
15 лет 18000 65000
20 лет 24000 142000
Получается, постепенно вкладывая в течение 20 лет по 100$ ежемесячно, в итоге вы получите 142 000 долларов.
При таких условиях на пассивный доход, равный вашей сегодняшней зарплате $1000, вы выйдете через 15 лет.
Если заходите получать ежемесячно в 2 раза больше — $2000, подождите еще 5 лет.
Есть такое правило удвоения капитала при заданной процентной ставке – «правило 72».
Удвоение происходит по формуле – 72 делим на процентную ставку.
Пример: 100$ при 12% ставке удвоятся через 72/12 =6 лет. Следующее удвоение произойдет еще через 6 лет.
100$ при 18% удвоятся через 72/18=4 года.
Здесь, конечно, речь идет единственном вложение средств в начале срока. Если вы будете ежемесячно дополнительно докладывать средства, суммы будут удваиваться еще быстрее. Рассчитать какая прибыль получится при вложении той или иной суммы на разных промежутках времени и при разном уровне доходности можно используя онлайн калькулятор с капитализацией и пополнением.
Сложный процент – Финансовая энциклопедия
Что такое Сложный процент?
Сложные проценты (или сложные проценты) – это проценты по кредиту или депозиту, рассчитываемые как на основе первоначальной основной суммы, так и накопленных процентов за предыдущие периоды. Считается, что сложный процент возник в Италии 17 века, сложный процент можно рассматривать как «процент на процент», и он заставляет сумму расти быстрее, чем простой процент , который рассчитывается только на основную сумму.
Считается, что сложный процент возник в Италии 17 века, сложный процент можно рассматривать как «процент на процент», и он заставляет сумму расти быстрее, чем простой процент , который рассчитывается только на основную сумму.
Ключевые моменты
- Сложные проценты (или сложные проценты) – это проценты, начисляемые на первоначальную основную сумму, которая также включает все накопленные проценты за предыдущие периоды по депозиту или ссуде.
- Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная на количество составных периодов минус один.
- Проценты могут быть увеличены по любому заданному графику периодичности, от непрерывного до ежедневного или ежегодного.
- При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение.
Скорость , при которой соединение начисления процентов зависит от частоты компаундирования, такой , что чем выше количество компаундирования периодов, тем больше сложные проценты. Таким образом, сумма сложных процентов, начисленных на 100 долларов США с начислением 10% годовых, будет ниже, чем сумма сложных процентов на 100 долларов США с начислением 5% годовых в течение того же периода времени. Поскольку эффект процентной ставки может приносить все более положительную прибыль на основе начальной основной суммы, ее иногда называют «чудом сложных процентов».
Таким образом, сумма сложных процентов, начисленных на 100 долларов США с начислением 10% годовых, будет ниже, чем сумма сложных процентов на 100 долларов США с начислением 5% годовых в течение того же периода времени. Поскольку эффект процентной ставки может приносить все более положительную прибыль на основе начальной основной суммы, ее иногда называют «чудом сложных процентов».
Расчет сложных процентов
Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная на количество составных периодов минус один. Затем из полученной стоимости вычитается общая первоначальная сумма ссуды.
Формула расчета сложных процентов:
Сложные проценты = Общая сумма основной суммы долга и процентов в будущем (или будущая стоимость) за вычетом суммы основного долга в настоящее время (или приведенной стоимости)
= [P (1 + i
= P [(1 + i ) n – 1]
(Где P = основная сумма, i = номинальная годовая процентная ставка в процентах, а n = количество периодов начисления сложных процентов. )
)
Возьмите трехлетний заем в размере 10 000 долларов США под 5% годовых. Какая будет сумма процентов? В этом случае это будет: 10 000 [(1 + 0,05) 3 – 1] = 10 000 [1,157625 – 1] = 1 576,25 доллара.
Рост сложных процентов
Используя приведенный выше пример, поскольку сложные проценты также учитывают накопленные проценты за предыдущие периоды, сумма процентов не будет одинаковой для всех трех лет, как это было бы с простыми процентами. Хотя общая сумма процентов, подлежащих выплате в течение трехлетнего периода по этому займу, составляет 1 576,25 долларов США, проценты, подлежащие выплате в конце каждого года, показаны в таблице ниже.
Периоды накопления
При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение. Основное правило состоит в том, что чем больше количество периодов начисления сложных процентов, тем больше сумма сложных процентов.
Следующая таблица демонстрирует разницу, которую может составить количество периодов начисления сложных процентов для ссуды в размере 10 000 долларов США с годовой процентной ставкой 10% в течение 10-летнего периода.
Сложные проценты могут значительно повысить доходность инвестиций в долгосрочной перспективе. В то время как вклад в размере 100 000 долларов, который получает 5% простых процентов, принесет 50 000 долларов процентов в течение 10 лет, сложные проценты в размере 5% на 10 000 долларов составят 62 889,46 долларов за тот же период.
Расчет компаундирования в Excel
Если со времен уроков математики прошло некоторое время, не бойтесь: есть удобные инструменты, которые помогут сложить числа. Многие калькуляторы (как карманные, так и компьютерные) имеют функции экспоненты, которые можно использовать для этих целей. Если возникают более сложные сложные задачи, их можно выполнить с помощью Microsoft Excel тремя разными способами.
- Первый способ рассчитать сложные проценты – это умножить новый баланс каждого года на процентную ставку. Предположим, вы вкладываете 1000 долларов на сберегательный счет с годовой процентной ставкой 5% и хотите рассчитать остаток через пять лет.
 n) – P». В третьей строке модуля введите «Завершить функцию». Вы создали макрос функции для расчета сложной процентной ставки. Продолжая работу с тем же листом Excel, приведенным выше, введите «Сложный процент» в ячейку A6 и введите «= Сложный_Процент (B1, B2, B3)». Это дает вам значение 276,28 доллара, что согласуется с первыми двумя значениями.
n) – P». В третьей строке модуля введите «Завершить функцию». Вы создали макрос функции для расчета сложной процентной ставки. Продолжая работу с тем же листом Excel, приведенным выше, введите «Сложный процент» в ячейку A6 и введите «= Сложный_Процент (B1, B2, B3)». Это дает вам значение 276,28 доллара, что согласуется с первыми двумя значениями.
Использование других калькуляторов
Как упоминалось выше, в Интернете предлагается ряд бесплатных калькуляторов сложных процентов, и многие портативные калькуляторы также могут выполнять эти задачи.
- Бесплатный калькулятор сложных процентов, предлагаемый на сайте Financial-Calculators.com, прост в использовании и предлагает выбор частоты от дня до года. Он включает в себя возможность выбора непрерывного сложения, а также позволяет вводить фактические календарные даты начала и окончания. После ввода необходимых данных расчета результаты показывают заработанные проценты, будущую стоимость, годовую процентную доходность (APY), которая является мерой, включающей начисление сложных процентов и дневные проценты.

- Investor.gov , веб-сайт, управляемый Комиссией по ценным бумагам и биржам США (SEC), предлагает бесплатный онлайн-калькулятор сложных процентов. Калькулятор довольно прост, но он позволяет вводить ежемесячные дополнительные депозиты основному лицу, что полезно для расчета доходов, когда вносятся дополнительные ежемесячные сбережения.
- Бесплатный онлайн-калькулятор процентов с несколькими дополнительными функциями доступен на TheCalculatorSite.com. Этот калькулятор позволяет производить расчеты для различных валют, учитывать ежемесячные депозиты или снятия, а также автоматически рассчитывать ежемесячные депозиты или снятия с поправкой на инфляцию.
Частота смешивания
Проценты могут быть увеличены по любому заданному графику периодичности, от ежедневного до ежегодного. Существуют стандартные графики частоты начисления сложных процентов, которые обычно применяются к финансовым инструментам.
Обычно для денежного рынка – часто ежедневно. Для жилищных ипотечных ссуд, ссуд под залог недвижимости, ссуд для личного бизнеса или счетов по кредитным картам обычно применяется ежемесячный график начисления сложных процентов.
Некоторые банки также предлагают так называемое непрерывное начисление сложных процентов, которое добавляет проценты к основной сумме в каждый возможный момент. С практической точки зрения, это не намного больше, чем ежедневное начисление сложных процентов, если вы не хотите вкладывать деньги и снимать их в тот же день.
Более частое начисление сложных процентов выгодно инвестору или кредитору. Для заемщика все наоборот.
Оценка временной стоимости денег
Понимание временной стоимости денег и экспоненциального роста, создаваемого сложным капиталом, важно для инвесторов, стремящихся оптимизировать свои доходы и распределение богатства.
Формула для получения будущей стоимости (FV) и текущей стоимости (PV) выглядит следующим образом:
FV = PV (1 + i) n и PV = FV / (1 + i) n
Например, будущая стоимость 10 000 долларов США составит 5% годовых в течение трех лет:
= 10 000 долларов США (1 + 0,05) 3
= 10 000 долл. США (1 157 625 долл. США)
= 11 576,25 долл. США
Приведенная стоимость 11 576,25 долларов США со скидкой 5% на три года:
= 11 576,25 долл. США / (1 + 0,05) 3
= 11 576,25 долл. США / 1 157 625 долл. США
= 10 000 долларов США
Обратное значение 1,157625, равное 0,8638376, в данном случае является коэффициентом дисконтирования.
Рассмотрение по правилу 72
Так называемое Правило 72 рассчитывает приблизительное время, в течение которого инвестиции удвоятся при заданной норме прибыли или процентах «i», и определяется выражением (72 / i). Его можно использовать только для годового начисления процентов.
Например, инвестиция с годовой доходностью 6% удвоится через 12 лет.
Таким образом, инвестиции с годовой доходностью 8% увеличатся вдвое за девять лет.
Совокупный годовой темп роста (CAGR)
Совокупный годовой темп роста (CAGR) используется для большинства финансовых приложений, которые требуют расчета единого темпа роста за период времени.
Допустим, ваш инвестиционный портфель вырос с 10 000 до 16 000 долларов за пять лет; что такое CAGR? По сути, это означает, что PV = – 10 000 долларов США, FV = 16 000 долларов США, nt = 5, поэтому переменная «i» должна быть вычислена. Используя финансовый калькулятор или Excel, можно показать, что i = 9,86%.
(Обратите внимание, что в соответствии с соглашением о движении денежных средств, ваши начальные инвестиции (PV) в размере 10 000 долларов США показаны с отрицательным знаком, поскольку они представляют собой отток средств. PV и FV обязательно должны иметь противоположные знаки, чтобы найти «i» в приведенном выше уравнение).
CAGR Реальные приложения
CAGR широко используется для расчета доходности за периоды времени для акций, паевых инвестиционных фондов и инвестиционных портфелей. CAGR также используется для определения того, превышал ли управляющий паевым инвестиционным фондом или управляющий портфелем рыночную норму прибыли в течение определенного периода времени. Если, например, рыночный индекс обеспечил совокупную доходность 10% за пятилетний период, но управляющий фондом получил только 9% годовой прибыли за тот же период, это означает, что он отстал от рынка.
CAGR также можно использовать для расчета ожидаемых темпов роста инвестиционных портфелей в течение длительных периодов времени, что полезно для таких целей, как накопление средств на пенсию. Рассмотрим следующие примеры:
Пример 1. Не склонный к риску инвестор доволен скромной годовой доходностью 3% по своему портфелю. Таким образом, ее нынешний портфель в 100 000 долларов через 20 лет вырастет до 180 611 долларов. Напротив, терпимый к риску инвестор, ожидающий годовой доходности 6% от своего портфеля, через 20 лет увидит, что 100 000 долларов вырастут до 320 714 долларов.
Напротив, терпимый к риску инвестор, ожидающий годовой доходности 6% от своего портфеля, через 20 лет увидит, что 100 000 долларов вырастут до 320 714 долларов.
Пример 2: CAGR можно использовать для оценки того, сколько нужно убрать, чтобы сэкономить для конкретной цели. Пара, которая хотела бы сэкономить 50 000 долларов в течение 10 лет на первоначальный взнос за кондоминиум, должна будет экономить 4 165 долларов в год, если они предполагают, что годовая прибыль (CAGR) составит 4% от своих сбережений. Если они готовы пойти на дополнительный риск и рассчитывать на среднегодовой темп роста 5%, им нужно будет экономить 3 975 долларов в год.
Пример 3: CAGR также можно использовать для демонстрации достоинств инвестирования в более раннем, чем в более позднем возрасте. Если цель состоит в том, чтобы сэкономить 1 миллион долларов к выходу на пенсию в возрасте 65 лет, исходя из среднегодового роста в 6%, 25-летнему человеку для достижения этой цели потребуется откладывать 6 462 доллара в год. С другой стороны, 40-летнему человеку нужно будет сэкономить 18 227 долларов, что почти в три раза больше, чтобы достичь той же цели.
С другой стороны, 40-летнему человеку нужно будет сэкономить 18 227 долларов, что почти в три раза больше, чтобы достичь той же цели.
- Среднегодовые темпы роста также часто возникают в экономических данных. Вот пример: ВВП Китая на душу населения увеличился с 193 долларов в 1980 году до 6091 долларов в 2012 году. Каков годовой рост ВВП на душу населения за этот 32-летний период? Темп роста «i» в данном случае составляет впечатляющие 11,4%.
Плюсы и минусы компаундирования
В то время как магия компаундирования привела к апокрифической истории о том, что Альберт Эйнштейн назвал его восьмым чудом света или величайшим изобретением человека, компаундирование также может работать против потребителей, у которых есть ссуды с очень высокими процентными ставками, например, задолженность по кредитной карте. Остаток по кредитной карте в размере 20 000 долларов США с ежемесячной процентной ставкой 20% приведет к общей сумме сложных процентов в размере 4 388 долларов США за год или около 365 долларов США в месяц.
С положительной стороны, магия начисления сложных процентов может работать вам на пользу, когда дело касается ваших инвестиций, и может стать мощным фактором создания богатства. Экспоненциальный рост за счет сложных процентов также важен для смягчения факторов разрушения богатства, таких как рост стоимости жизни, инфляция и снижение покупательной способности.
Паевые инвестиционные фонды предлагают инвесторам один из самых простых способов воспользоваться преимуществами сложных процентов . Если вы решите реинвестировать дивиденды, полученные от взаимного фонда, вы приобретете больше акций фонда. Со временем накапливается больше сложных процентов, и цикл покупки большего количества акций будет продолжать способствовать росту стоимости инвестиций в фонд.
Рассмотрим инвестицию в паевой инвестиционный фонд, открытый с начальными 5000 долларов и ежегодным приростом в 2400 долларов. При средней годовой доходности 12% за 30 лет будущая стоимость фонда составляет 798 500 долларов. Сложный процент – это разница между денежными средствами, внесенными в инвестиции, и фактической будущей стоимостью инвестиций. В этом случае, если внести 77 000 долларов или всего 200 долларов в месяц в течение 30 лет, сложные проценты составят 721 500 долларов от будущего баланса. Конечно, доходы от сложных процентов подлежат налогообложению, если только деньги не находятся на счете, защищенном от налогов; обычно он облагается налогом по стандартной ставке, установленной для налоговой категории налогоплательщика.
Сложный процент – это разница между денежными средствами, внесенными в инвестиции, и фактической будущей стоимостью инвестиций. В этом случае, если внести 77 000 долларов или всего 200 долларов в месяц в течение 30 лет, сложные проценты составят 721 500 долларов от будущего баланса. Конечно, доходы от сложных процентов подлежат налогообложению, если только деньги не находятся на счете, защищенном от налогов; обычно он облагается налогом по стандартной ставке, установленной для налоговой категории налогоплательщика.
Инвестиции со сложными процентами
Инвестор, который выбирает план реинвестирования в рамках брокерского счета, по сути, использует возможность начисления сложных процентов во все, что он инвестирует. Инвесторы также могут получить сложный процент при покупке облигации с нулевым купоном. Традиционные выпуски облигаций обеспечивают инвесторам периодические выплаты процентов на основе первоначальных условий выпуска облигаций, и, поскольку они выплачиваются инвестору в форме чека, проценты не складываются. Бескупонные облигации не отправляют инвесторам процентные чеки; вместо этого облигации этого типа приобретаются со скидкой к их первоначальной стоимости и со временем растут. Эмитенты бескупонных облигаций используют возможность начисления сложных процентов для увеличения стоимости облигации, чтобы она достигла своей полной цены к моменту погашения.
Бескупонные облигации не отправляют инвесторам процентные чеки; вместо этого облигации этого типа приобретаются со скидкой к их первоначальной стоимости и со временем растут. Эмитенты бескупонных облигаций используют возможность начисления сложных процентов для увеличения стоимости облигации, чтобы она достигла своей полной цены к моменту погашения.
Компаундирование также может работать на вас при выплате кредита. Например, если вы будете выплачивать половину ипотечного платежа дважды в месяц вместо того, чтобы вносить полный платеж один раз в месяц, это сократит ваш период погашения и сэкономит вам значительную сумму процентов.
Кстати о займах…
Как узнать, есть ли проценты
Закон о правде в кредитовании (TILA) требует, чтобы кредиторы раскрывали условия кредита потенциальным заемщикам, включая общую сумму процентов в долларах, подлежащую выплате в течение срока действия кредита, и то, начисляются ли проценты простым или сложным образом.
Другой метод – сравнить процентную ставку по ссуде с ее годовой процентной ставкой (APR), которую TILA также требует от кредиторов. Годовая процентная ставка конвертирует финансовые расходы по вашему кредиту, которые включают все проценты и комиссии, в простую процентную ставку. Существенная разница между процентной ставкой и АТР означает один или оба из двух сценариев: Ваш кредит использует сложные проценты, или она включает в себя значительные сборы кредита в дополнение к процентам. Даже когда речь идет о ссуде одного и того же типа, диапазон годовых может сильно различаться между кредиторами в зависимости от комиссий финансового учреждения и других затрат.
Годовая процентная ставка конвертирует финансовые расходы по вашему кредиту, которые включают все проценты и комиссии, в простую процентную ставку. Существенная разница между процентной ставкой и АТР означает один или оба из двух сценариев: Ваш кредит использует сложные проценты, или она включает в себя значительные сборы кредита в дополнение к процентам. Даже когда речь идет о ссуде одного и того же типа, диапазон годовых может сильно различаться между кредиторами в зависимости от комиссий финансового учреждения и других затрат.
Вы заметите, что процентная ставка, которую вы взимаете, также зависит от вашего кредита. Ссуды, предлагаемые тем, у кого есть отличная кредитоспособность, имеют значительно более низкие процентные ставки, чем те, которые взимаются с лиц с плохой кредитной историей .
Часто задаваемые вопросы
Каково простое определение сложных процентов?
Сложные проценты относятся к явлению, при котором проценты, связанные с банковским счетом, ссудой или инвестициями, со временем растут экспоненциально, а не линейно. Ключом к пониманию концепции является слово «составной». Предположим, вы инвестируете 100 долларов в бизнес, который ежегодно выплачивает вам 10% дивидендов. У вас есть выбор: вложить эти дивиденды в наличные или реинвестировать эти выплаты в дополнительные акции. Если вы выберете второй вариант, реинвестируя дивиденды и складывая их вместе с вашими первоначальными инвестициями в 100 долларов, то получаемая вами доходность со временем начнет расти.
Ключом к пониманию концепции является слово «составной». Предположим, вы инвестируете 100 долларов в бизнес, который ежегодно выплачивает вам 10% дивидендов. У вас есть выбор: вложить эти дивиденды в наличные или реинвестировать эти выплаты в дополнительные акции. Если вы выберете второй вариант, реинвестируя дивиденды и складывая их вместе с вашими первоначальными инвестициями в 100 долларов, то получаемая вами доходность со временем начнет расти.
Кому выгодны сложные проценты?
Проще говоря, сложные проценты приносят пользу инвесторам, но значение слова «инвесторы» может быть довольно широким. Банки, например, получают выгоду от сложных процентов, когда ссужают деньги и реинвестируют полученные проценты в выдачу дополнительных ссуд. Вкладчики также получают выгоду от сложных процентов, когда они получают проценты по своим банковским счетам, облигациям или другим инвестициям. Важно отметить, что, хотя термин «сложные проценты» включает в себя слово «проценты», эта концепция применяется за пределами ситуаций, в которых обычно используется слово «проценты», таких как банковские счета и ссуды.
Могут ли сложные проценты сделать вас богатым?
Да. Фактически, сложные проценты, возможно, являются самой мощной силой для создания богатства из когда-либо задуманных. Есть записи о купцах, кредиторах и различных бизнесменах, которые использовали сложные проценты, чтобы разбогатеть буквально на тысячи лет. В древнем городе Вавилон, например, более 4000 лет назад глиняные таблички использовались для обучения студентов математике сложных процентов. В наше время Уоррен Баффет стал одним из самых богатых людей в мире благодаря бизнес-стратегии, которая предусматривала усердное и терпеливое увеличение прибыли от его инвестиций в течение длительных периодов времени. Вполне вероятно, что в той или иной форме люди будут использовать сложные проценты для создания богатства в обозримом будущем.
#ССложный процент на форекс увеличивает вашу прибыль
Сложный процент позволяет увеличивать прибыль. Он увеличивает капитализацию, что обеспечивает все возрастающие доходы. Понятие эффективной ставки сложных процентов играет существенную роль в трейдинге на форекс. Важно научиться управлять собственным депозитом, чтобы использовать свои инвестиции полезным образом.
Понятие эффективной ставки сложных процентов играет существенную роль в трейдинге на форекс. Важно научиться управлять собственным депозитом, чтобы использовать свои инвестиции полезным образом.
Что такое сложные проценты?
Как известно, проценты бывают простыми и сложными. Приведем пример простого процента: допустим, на счет в банке положили $ 1000 и ежемесячно прибыль составляет 1 %, полученные $ 10 каждый месяц снимаются со счета. Прибыль фиксированная, доход неизменен.
Если воспользоваться депозитом со сложными процентами, то каждый месяц к основному депозиту будет добавляться прибыль, с которой в следующем месяце тоже начисляться проценты. Это и есть сложный процент.
Может показаться, что разница несущественная. И, действительно, на кротком отрезке времени разница по простым и сложным процентам весьма невелика. Но при длительной инвестиции результат удивляет — сложные проценты обеспечивают гораздо большую прибыль. В этом несложно убедиться, если воспользоваться калькулятором сложных процентов.
Сложные проценты в реальной жизни встречаются достаточно часто. Самыя очевидный пример – инвестиция денег в банк с капитализацией вклада.
О формуле сложного процента
Оказалось, что многие трейдеры не имеют представления об особенностях сложного процента. Но его использование может оказаться очень эффективным для вас.
Начисление процентов на проценты (сложный процент) рассчитывается по простой формуле сложных процентов. Она выглядит так.
Прибыль = [Р (1 + г) n] – Р
Р – первоначальная сумма;
r – ставка;
n – период инвестирования.
Теперь можно посчитать прибыль от инвестирования на 5 лет $10 000 с процентной ставкой 10 %. С учетом реинвестирования прибыли получаем общую сумму 6 105.1. Если посчитать простой процент, то общая сумма кажется равной 5 000. Таким образом, разница вполне очевидна, формула сложных процентов обеспечивает большую прибыль.
Может показаться, что разница в тысячу с небольшим долларов не слишком велика, да еще и пять лет ждать. Но в трейдинге сложный процент может проявить себя еще более впечатляюще.
Но в трейдинге сложный процент может проявить себя еще более впечатляюще.
Понять это можно при анализе предложенной формулы. Нужно отметить, что экспоненциальный рост обеспечивает наибольшее возможное увеличение основной величины.
Итак, увеличение прибыли возможно при увеличении любого параметра формулы. Можно оставить основную сумму инвестиции, но поменяем период инвестиции. Допустим, реинвестирование происходит ежемесячно, что означает 60 месяцев депозита при процентной ставке 10 %, деленной на 12 месяцев, то есть 0.833 % в месяц. После несложных вычислений получается сумма 6 449,8 доллара. Это значит, что более частая капитализация сильно прибыльнее.
Если же реинвестировать доход каждый день, результат окажется еще более значимым. Все эти математические выкладки производят сильное впечатление. Но практика не позволяет увеличивать прибыль трейдера бесконечно. В одни дни у вас на рынке могут быть убытки, в другие — прибыль. Воспользоваться приведенной формулой в этих условиях достаточно сложно. Простые и сложные проценты нужно использовать в благоприятных условиях.
Простые и сложные проценты нужно использовать в благоприятных условиях.
Трейдинг в инвестиционной плоскости
Извечная тема заработка на валютном рынке вызывает живой интерес у многих трейдеров. Вопрос трейдинга и инвестиций оказался очень актуальным сегодня. Его рассмотрение требует определенных дополнительных знаний, позволяющих выносить торговые риски за пределы рынка.
Достаточно представить себе, что каждый дополнительно полученный доллар делает вероятность его потери более высокой. Замечено, что если деньги находятся исключительно на торговом счету, а их объемы непрерывно увеличиваются, то трейдер неминуемо потеряет их. Возможно, получится сохранить первоначальную сумму, но время будет проведено зря. Риски торговли слишком велики.
Если использовать капитализацию основного депозита на форекс, можно добиться определенных успехов. Депозит растет по закону экспоненты, что математически означает значительное увеличение основного капитала. Но доход в тысячу процентов, который может быть реализован, если верить математическим выкладкам, слишком велик. На его получение в реальности рассчитывать вряд ли стоит.
На его получение в реальности рассчитывать вряд ли стоит.
Это означает, что модель роста по экспоненте ограничена с точки зрения применимости на практике. Для физиков прекрасно известно, что экспонента моделирует взрыв.
Экспоненциальный рост ставок при определенных условиях и стабильной прибыли принесет неплохой доход, но нужно быть уверенным в границах применимости этой математической модели.
Срок инвестиций определяется вполне конкретными условиями, а не указаниями профессионалов, хоть и очень уважаемых. Многие инвесторы, кроме того, не склонны действовать с прицелом на далекое будущее, а они в этом правы с учетом современных реалий.
Изучите в тему полезный материал о том, как минимизировать риски на форекс.
Учет фактора времени
При рассмотрении графика сложного процента становится очевидно, что его вид зависит от параметров формулы. Простое изменение масштаба или параметров позволяет получить график другой экспоненты просто изменением масштаба времени. 2. (3.1) В случае 1 + zt выражение (1.5) в интервале [0, 1] равно u (0 = l + rt, 0 <*) <1.
2. (3.1) В случае 1 + zt выражение (1.5) в интервале [0, 1] равно u (0 = l + rt, 0 <*) <1.
- Таким образом, сила (3.1) точно характеризует простой случай процентов для годовой процентной ставки i: простую схему начисления процентов для годовой процентной ставки i
и постоянную процентную ставку 6 (t) = 6, соответствующую годовой процентной ставке i. Людмила Фирмаль
Другими словами, мы пытаемся сравнить два эквивалентных процесса накопления в первый год «их жизни» Рисунок 3.1: Сравнение простых и сложных схем накопления скорости На рисунке 3.1
В упражнении 5 предлагается математически подтвердить этот вывод.Кроме того, в некотором смысле наиболее выгодным моментом блока питания является то, что функция y = (14- 🙂 *;
- Пример 3.1: Запишите уравнение для точки PSU в = = (i) 3.1 принимает максимальное значение, указывая, что значение to для малого i составляет около 1/2, а в ( 0,1) Определить решение 1.
 — ~ -, r- * ° -3. В ПД.1 6 = 0,09531, поэтому (0,1) = 1р (0,1 / 0,09531) / 0,09531 = В (1,04920 ) /0.09531 = 0.5036 •
— ~ -, r- * ° -3. В ПД.1 6 = 0,09531, поэтому (0,1) = 1р (0,1 / 0,09531) / 0,09531 = В (1,04920 ) /0.09531 = 0.5036 •Рисунок 3.1 (слева) указывает, что функция y = 1 4-it на интервале (0,1) более выгодна для кредитора, поскольку функция y = (14-i) 1 выше
Вышеуказанные факты четко объяснены: начало интервала (0, 1) интенсивности (3.1) выше, чем постоянная интенсивность y = 6, и к концу ситуации ситуация меняется на противоположную.
Это только указывает на реальную власть, и в реальной жизни интервал, в котором используется простой интерес, ограничен одним годом.
В случае целесообразно добавить, что использование сложных процентов составляет почти 100%, но, конечно, это происходит, когда они используются в транзакциях менее года.
Часто используется в краткосрочных операциях. Длится меньше года. Однако у них есть другие области применения.
Это связано с тем, что при использовании периодических ставок в финансовых операциях за период (связанный с рассматриваемым периодом) формула сложного процента не дает достаточного описания изменения стоимости денежной единицы с течением времени.

Следовательно, требуется упрощенное приближение, часто опирающееся на простые пропорции.
Смотрите также:
Узнайте разницу между простым и сложным процентом в Excel
Процентная ставка, используемая в самых различных финансовых приложениях, — это сумма, необходимая для получения данного кредита. Его можно рассчитать двумя способами: простой процент и сложный процент. Его база расчета определяется месячными, квартальными, полугодовыми или годовыми ставками в большинстве переговоров, и в статье мы увидим некоторые применения обоих.
Вы знаете разницу между ними? У вас есть идея правильной формулы, которая будет использоваться в Excel? Посмотрите ниже разницу между простым и сложным процентом в Excel
Разница между простым и сложным процентом в Excel
Простыми процентами сумма получается из первоначальной стоимости (заемного капитала) в определенный период времени, и нет никакого накопления процентов.
 Таким образом, независимо от того, насколько ваши деньги ценят с течением времени, сумма всегда рассчитывается по первоначальной стоимости или добавляется. Хотя более практичные, простые процентные ставки не используются в реальной жизни. Например, если вы подаете заявку на кредит или вкладываете свои деньги, расчеты всегда выполняются с учетом сложных процентов.
Таким образом, независимо от того, насколько ваши деньги ценят с течением времени, сумма всегда рассчитывается по первоначальной стоимости или добавляется. Хотя более практичные, простые процентные ставки не используются в реальной жизни. Например, если вы подаете заявку на кредит или вкладываете свои деньги, расчеты всегда выполняются с учетом сложных процентов.В отношении сложных процентов сумма получается из накопления процентов по первоначальной стоимости (заемному капиталу) в определенный период времени. Например, если я делаю инвестиции R $ 100, для 3 лет, со сложным процентом 10% в год, каков будет мой окончательный доход?
- Год 1 = R $ 100 x 1,1 = R $ 110
- Год 2 = R $ 110 x 1,1 = R $ 121
- Год 3 = R $ 121 x 1,1 = R $ 133,1
Доходность 33,1 реала. Если бы мы проводили эти расчеты с использованием только простых процентов, доход составил бы 30 реалов. Это может показаться небольшим, но это процент, который может быть очень положительным или отрицательным в случае более длительных периодов, больших сумм или более высоких процентных ставок.
 Вот почему мы говорим, что и для простых процентов, и для сложных процентов требуются три фактора: заемный (или инвестированный) капитал, срок платежа и процентная ставка, подлежащая начислению.
Вот почему мы говорим, что и для простых процентов, и для сложных процентов требуются три фактора: заемный (или инвестированный) капитал, срок платежа и процентная ставка, подлежащая начислению.Простой интерес к Excel
Математическая формула для вычисления простого интереса:
J = cin
c = заемный капитал (начальная стоимость)
i = процентная ставка (ежемесячно, ежеквартально, полугодовая, годовая, среди прочих, должна учитываться для правильного расчета)
n = крайний срок для оплаты (также учитывайте период времени для проведения правильного расчета)
Давайте посмотрим на пример расчета простого процента в Excel:
В приведенной выше таблице есть ячейки 3, где пользователь вводит значения и ячейки 4, которые выполняют вычисления на основе введенных данных. Все это как способ иллюстрировать для вас расчет простых интересов.
В ячейке A4 будет заполнена суммой заемных средств, то есть начальным капиталом.
 Уже ячейка B4 представляет собой процентную ставку, установленную в 2% ежемесячно в этом примере. Наконец, член ячейки C4 относится к месячному периоду оплаты, в случае 10 месяцев.
Уже ячейка B4 представляет собой процентную ставку, установленную в 2% ежемесячно в этом примере. Наконец, член ячейки C4 относится к месячному периоду оплаты, в случае 10 месяцев.Формула, вставленная в ячейку D4 é = A4 * B4 и представляет собой сумму ежемесячных уплаченных процентов.
Кроме того, клеточная формула E4 é = A4 / C4 + D4 и относится к выплаченной ежемесячной сумме.
Формула = A4 * B4 * C4 постоянный в объединенных ячейках B6, C6, D6 и E6 представляет собой общий процент, уплаченный по кредиту.
И формула =A4 + B6 объединенных ячеек B7, C7, D7 и E7 общая сумма, уплаченная за кредит.
Составной интерес в Excel
Математическая формула для расчета сложных процентов:
М = с * (1 + я)t
M = сумма
c = заемный капитал (начальная стоимость)
i = процентная ставка (ежемесячный, квартальный, полугодовой, годовой период, среди прочего, необходимо учитывать для выполнения правильного расчета)
t = крайний срок платежа (также следует учитывать период времени для правильного расчета)
Давайте посмотрим на пример в Excel:
Мы используем те же данные из простой таблицы интересов: R $ 20.
 A13
A13
Интерес
- C4 CELL = B4- $ B $ 1
- C5 CELL = B5- $ B $ 1
- C6 CELL = B6- $ B $ 1
- C7 CELL = B7- $ B $ 1
- C8 CELL = B8- $ B $ 1
- C9 CELL = B9- $ B $ 1
- C10 CELL = B10- $ B $ 1
- C11 CELL = B11- $ B $ 1
- C12 CELL = B12- $ B $ 1
- C13 CELL = B13- $ B $ 1
Таким образом, анализируя клетки B13 e C13 которые представляют соответственно общую накопленную сумму и сумму уплаченных процентов, мы можем отметить резкую разницу значений по отношению к простым процентам, имея в качестве параметра тот же капитал, вложенный, такую же процентную ставку и тот же период времени.
Несколько более простой способ — использовать функцию PGTO в самом Excel, что позволяет использовать этот тип вычислений.
Разница между простым и сложным интересом в Excel и реальной жизни
Я считаю, что самое главное знать о сложном и простом интересе к Excel заключается в том, что это не так сложно делать, если вы понимаете логику накопления сложных процентов. Уже в реальной жизни эта логика еще важнее, потому что именно она может поглотить вас долгами или хорошим доходом.
Уже в реальной жизни эта логика еще важнее, потому что именно она может поглотить вас долгами или хорошим доходом.
Если вы хотите узнать больше о Excel, проверьте наши курсы для начинающих и промежуточных или продвинутых курсов на нашей платформе, Воспользуйтесь также, чтобы убрать свои сомнения в наших форум об Excel или здесь, в комментариях!
2 реальных примера силы сложного процента
Этот пост может содержать партнерские ссылки, что означает, что если вы совершите покупку по ссылке, я могу получить небольшую комиссию без каких-либо дополнительных затрат для вас. Заработок используется для поддержания работы этого веб-сайта. Пожалуйста, прочтите мою страницу отказа от ответственности для получения дополнительной информации. Я всегда включаю только те ресурсы, которые лично использую и люблю. Я уверен, что вы уже слышали о силе сложных процентов и о том, как важно не просто инвестировать в свою пенсию, но сделать это как можно раньше.
Когда я учился в старшей школе, заставкой на семейном компьютере был баннер с надписью « Сохраните 10% своего дохода с 18 лет и выйдите на пенсию в 45 !»
Я должен отдать должное моему отцу за то, что он пытался воодушевить меня и мою сестру любым возможным способом сэкономить деньги, как только мы начали их зарабатывать.
Но когда ты молод, трудно заглядывать так далеко вперед. И если вы на самом деле не видите числа в реальном примере, трудно поверить в на самом деле .
Иногда все, что нужно для этого последнего толчка, чтобы начать экономить больше, — это увидеть соответствующий пример. Или два.
Дело в том, что сила сложных процентов высвобождается только со временем. Чем раньше вы начнете экономить, тем лучше. Либо чем короче время, которое вы потратите на накопление денег, либо тем меньше денег вы должны сэкономить с течением времени.
Если вы начнете поздно, вам придется сэкономить намного больше денег, чтобы наверстать упущенное. В этом посте я рассмотрю два примера, которые наглядно это демонстрируют.
В этом посте я рассмотрю два примера, которые наглядно это демонстрируют.
Два реальных примера силы сложных процентов
Пример №1: Все откладывают одинаковую сумму, но начинают в разное время.
Пример № 2: Все заканчивают с одинаковой суммой, но должны скорректировать сэкономленную сумму, чтобы она была там.
Пример №1: Возможности раннего старта
В этом первом примере мы смотрим, что произошло бы, если бы три разных человека сэкономили одинаковую сумму денег, но начали откладывать в разное время своей жизни.
Все они начинают экономить 1000 долларов в месяц и продолжают это делать в течение 10 лет. Каждый из них хочет выйти на пенсию к 55 годам.
- Карли начинает откладывать сбережения в возрасте 20 лет и прекращает работу к 30 годам.
- Том начинает делать сбережения в возрасте 30 лет и прекращает работу в 40 лет.
- Сара начинает еще позже, ожидая накопления до 40 лет и заканчивая в 50 лет.
Поскольку все они экономят одну и ту же 1000 долларов в месяц в течение 10 лет, они вносят 120 000 долларов. Однако к моменту выхода на пенсию в возрасте 55 лет их стоимость портфеля сильно различается.
Однако к моменту выхода на пенсию в возрасте 55 лет их стоимость портфеля сильно различается.
Допущения
- Годовая процентная ставка 7%, начисленная ежемесячно
- Стоимость портфеля 0 долларов на начало инвестирования
Результаты
К 55 годам:
- Carly приобрела чуть менее 1 миллиона долларов для выхода на пенсию .
- Том сэкономил чуть менее 500 000 долларов.
- У Сары, к сожалению, осталось чуть меньше 250 000 долларов на пенсию.
Благодаря силе сложных процентов Карли начала рано и поэтому смогла расслабиться и наблюдать, как ее сбережения продолжают расти и быстро расти с течением времени. Даже когда она не экономила активно.
Примечание. Все расчеты произведены с помощью калькулятора сложных процентов с сайта калькулятора.
Убрать
Предполагая, что Карли может экономно жить на пенсии, она действительно может оставить свою работу в возрасте 55 лет. Используя правило 4% , она может снимать 40 000 долларов в год на расходы на проживание. У Тома, однако, будет только половина этой суммы, 20 000 долларов, а у Сары — еще половина того, что у Тома. Какой бы бережливой ни была Сара, вряд ли она сможет прожить на 10 тысяч долларов в год.
Используя правило 4% , она может снимать 40 000 долларов в год на расходы на проживание. У Тома, однако, будет только половина этой суммы, 20 000 долларов, а у Сары — еще половина того, что у Тома. Какой бы бережливой ни была Сара, вряд ли она сможет прожить на 10 тысяч долларов в год.
Если мы увеличим это число до 65 лет, цифры будут еще более шокирующими.
- У Карли будет 2 миллиона долларов на пенсию или 80 000 долларов пенсионного дохода в год. Всего за 10 лет ей удалось удвоить стоимость своего портфеля. Опять же, без каких-либо взносов после 30 лет.
- У Тома было бы чуть меньше 1 миллиона долларов, чего хватило бы на скромную пенсию.
- Саре все равно не хватит накоплений, всего 500 000 долларов.
Мораль истории: начать экономить как можно раньше.
Пример № 2: Сколько вам нужно накопить, чтобы достичь своей пенсионной цели?
Давайте теперь рассмотрим сценарий, в котором вы хотите накопить пенсионные накопления в размере 1,5 миллиона долларов. Сколько вам нужно накопить, чтобы достичь этой пенсионной цели?
Сколько вам нужно накопить, чтобы достичь этой пенсионной цели?
Ну это зависит от , когда начинаешь экономить.
Давайте еще раз рассмотрим три разных примера.
- Карли начинает экономить 500 долларов в месяц с 20 лет
- Том начинает экономить 1000 долларов в месяц с 30 лет
- Сара начинает экономить 2000 долларов в месяц с 40 лет
Допущения
- Годовая процентная ставка 7%, ежемесячно
- Ежегодное увеличение взносов на 5%
- Стоимость портфеля 0 долларов в начале инвестирования
Примечание. Почему ежегодные взносы увеличиваются на 5%? Это может показаться недостижимым, но если учесть инфляцию, рост стоимости жизни, взносы работодателей, образование и накопленный опыт, а также противодействие увеличению образа жизни с течением времени, это вполне выполнимо.
Результаты
- Карли может выйти на пенсию в возрасте 54 лет. Общая сумма депозита за 34 года составляет 510 000 долларов.
 Стоимость ее портфеля после выхода на пенсию составляет 1,5 миллиона долларов. Если она действительно дождется выхода на пенсию в возрасте 60 лет, она сэкономит чуть более 2,5 миллиона долларов.
Стоимость ее портфеля после выхода на пенсию составляет 1,5 миллиона долларов. Если она действительно дождется выхода на пенсию в возрасте 60 лет, она сэкономит чуть более 2,5 миллиона долларов. - Том может выйти на пенсию в возрасте 57 лет. Общая сумма депозита за 27 лет составляет 650 000 долларов. Стоимость его портфеля после выхода на пенсию составляет чуть более 1,5 миллиона долларов. Если Том продержится еще 3 года, у него будет более 2 долларов.1 миллион пенсионных сбережений.
- Сара может выйти на пенсию в возрасте 60 лет. Общая сумма депозита за 20 лет составляет 790 000 долларов. Стоимость ее портфеля после выхода на пенсию составляет 1,55 миллиона долларов.
Уберите
С помощью сложных процентов, чем раньше вы начнете экономить, тем меньше вам придется откладывать со временем. Начните раньше, а затем позвольте сложным процентам сделать за вас большую часть работы.
Если вы начнете поздно, вам придется сэкономить больше, чтобы компенсировать нехватку времени и эффекты сложных процентов.
Связанные показания от Stepping Stones к FI
Применение концепции сложных процентов во всех сферах жизни
Вы бы предпочли миллион долларов сегодня или пенни, который удваивается каждый день в течение 30 дней? Сложные проценты существуют во всех сферах жизни.
Одна из моих основных жизненных философий — выполнять простые повседневные действия и дисциплинировать каждый день, чтобы немного приблизиться к своим целям. Я знаю, что не достигну своих целей ни сегодня, ни на следующей неделе, ни через неделю.
НО со временем, может быть, через несколько месяцев или несколько лет спустя, я добьюсь цели и достигну большего, чем я мог себе представить.
В этом посте я затрону самую важную концепцию личных финансов — сложных процентов.
Что такое сложный процент?
Сложные проценты — это, по сути, «проценты на ваши проценты» или, другими словами, рост ваших инвестиций с учетом предыдущего роста тех же инвестиций.
Один из простейших примеров сложных процентов заключается в следующем: вы бы предпочли получить 1 миллион долларов сегодня или предпочли бы взять пенни, но удваивать его каждый день в течение месяца?
В первый день у вас 2 цента, во второй день у вас 4 цента, в третий день у вас есть 8 центов … через две недели у вас есть 81,92 доллара. Угадайте что? В конце месяца вы получаете более 10 миллионов долларов.
Вы начали с копейки, что случилось? Это сила времени и сложения.
Да, вы начали с небольшой суммы, и долгое время у вас не было много, но 30 дней спустя, бум, 10 миллионов долларов — намного больше, чем 1 миллион долларов !!!
“ Сложные проценты — это восьмое чудо мира. Тот, кто понимает это, зарабатывает… тот, кто не… платит ». — Альберт Эйнштейн
Реальный пример сложных процентов
В мире личных финансов сложный процент может повлиять на вас несколькими способами, но я остановлюсь на двух: ваши инвестиции и ваш долг.
Как сложный процент влияет на ваши инвестиции
Допустим, вы инвестировали в актив, который приносит в среднем 7% годовых, и предположим, что вы инвестируете 10 000 долларов в первый год.
Через год у вас будет 10 000 долларов ваших первоначальных инвестиций и 700 долларов роста.
Хотя да, 700 долларов было бы здорово взять и потратить, вы решаете оставить их, потому что теперь эти 700 долларов вырастут на 7% в дополнение к остальной части ваших первоначальных инвестиций в 10000 долларов.
По прошествии второго года у вас теперь есть 11 449 долларов (10 000 + 700 долларов + 700 + 700 долларов * 7%)
Опять же, вы решаете оставить его, так как теперь оба $ 700 будут расти в дополнение к вашим первоначальным инвестициям.
За 30 лет рост довольно большой: ваши первоначальные инвестиции в размере 10 000 долларов стоят 76 123 доллара!
По прошествии 1 года у вас почти не осталось ничего, кроме ваших первоначальных инвестиций. Но через 30 лет ваши первоначальные вложения более чем в 7 раз превышают ваши первоначальные инвестиции! В этом сила сложения.
Но через 30 лет ваши первоначальные вложения более чем в 7 раз превышают ваши первоначальные инвестиции! В этом сила сложения.
График сложных процентов
Начальная сумма: 10 000 $ | Дополнительно ежегодно: $ 0 | Темп роста: 7,0%
Стоимость через 30 лет: 76 122,6 долл. США
График создан в Financial Toolbelt
Как сложный процент влияет на ваш долг
Допустим, вы взяли какой-то долг.
Теперь вместо увеличения инвестиций вы платите проценты по ссуде в банке или другом учреждении.
Я создал пример, в котором у пользователя были 2 кредитные карты, ипотека, автокредит и студенческий заем на общую сумму 246 500 долларов.
Выплачивая дополнительно 25 долларов в месяц и применяя метод выплаты долга, в этом примере есть потенциальная экономия не менее 49 915 долларов!
Как достигается эта экономия?
Добавляя каждый месяц немного больше к запланированному платежу по долгу, вы можете позволить начислению сложных процентов и сократить время, необходимое для погашения вашего долга.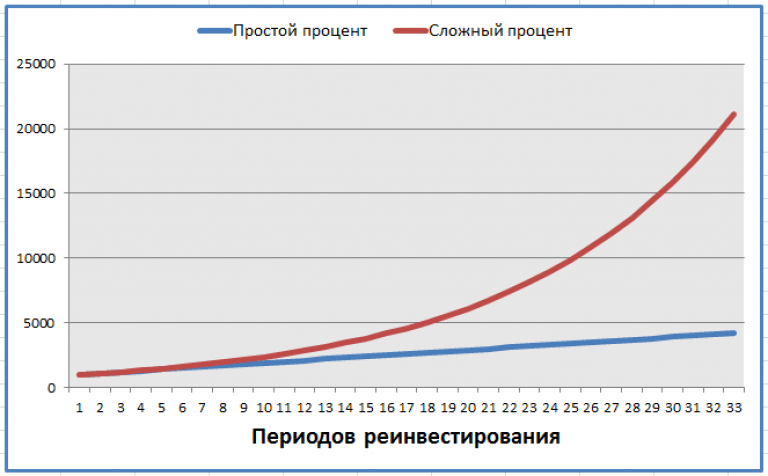
Сложные проценты могут работать на вас ИЛИ против вас. Что вы выберете?
Применение концепции сложных процентов в вашей жизни
О внутреннем вдохновителе, в то время как личные финансы — одна из моих задач, другой фокус — самосовершенствование и личное развитие.
Как я уже упоминал во вступлении, одна из моих основных философий — применение компаундирования во многих сферах моей жизни.
Прирост НИКОГДА линейный.
В мире, наполненном растворимым кофе, растворимым завтраком, мгновенным кредитом, мгновенными покупками, мгновенной информацией и круглосуточными новостями, мы подошли опасно близко к тому, чтобы потерять связь с реальностью и поверить в то, что у нас есть доступ к мгновенной жизни . Но life — это не кликабельная ссылка.
Начиная с любой области, в которой вы хотите стать лучше, рост невероятно медленный.
Вспомните время, когда вы были новичком в чем-то, в чем хотели стать лучше.
Мне нравится пример того, как я начал тренироваться: я был слаб и едва мог сделать несколько отжиманий.
В следующий раз, когда я тренировался, я мог сделать только 1 отжимание еще раз, но это был прогресс. В следующий раз я мог сделать 2 подхода по 5. После нескольких тренировок я сделал 3 подхода по 8.
После нескольких лет тренировок уже не исключено 30 отжиманий подряд.То, что начиналось менее чем с 5 отжиманий подряд, превратилось во многие.
Это одна и та же концепция в жизни во всем, что вы хотите: личные финансы, образование, здоровье и т. Д.
Станьте финансово успешным, один месяц за месяц
В этом блоге у меня есть куча других статей о личных финансах. Эти статьи о личных финансах помогут вам стать лучше в финансовом отношении. Вот список всех сообщений:
Скажу откровенно: вы не разбогатеете, просто прочитав то, что я написал, и сэкономите 100 долларов в этом месяце.
Вы, вероятно, не станете богатым, экономя 100 долларов каждый месяц в этом году.
НО, экономить 100 долларов в месяц на 10, 20 или 30 лет? Вы станете богатым.
Платить дополнительно 100 долларов по ипотеке на 10 или 20 лет? Вы будете свободны от долгов.
Экономить 10 000 долларов в год в течение 10, 20 или 30 лет? Привет, клуб двойной запятой! (1,000,000 состоит из 2 запятых 😉)
Примите простое решение разбогатеть сегодня, и я знаю, что если приложить постоянные усилия в течение долгого времени, вы добьетесь огромного успеха.
Заключение по применению концепции сложных процентов
Помните: простые повседневные действия и дисциплина со временем дадут огромные результаты.
Недостаточно сделать что-то один раз.
Делать что-то дважды — тоже не то.
Делаете что-то ежедневно в течение недель и месяцев? Я знаю, ты доберешься туда.
Читатели: как вы применяете концепцию сложных процентов? Вы видели, как в вашей жизни или в финансах происходило начисление сложных процентов?
Эрик
Об авторе
Привет! Я Эрик, создатель блога The Mastermind Within.
Я страстно желаю помочь вам стать лучше как личность, улучшить свои финансы и со временем создать жизнь своей мечты.
Я верю, что через постановку целей, критическое мышление и целенаправленную жизнь и действия вы можете управлять своей жизнью, выигрывать деньгами и встать на путь свободы.
Получите бесплатное руководство по целям ниже или просмотрите 6 страниц портала после формы руководства.
Какие виды использования сложных процентов в бизнесе? | Малый бизнес
Автор Chron Contributor Обновлено 16 февраля 2021 г.
Владельцы малых предприятий часто имеют ограниченные источники дохода и дополнительно обременены расходами, что чрезвычайно затрудняет внесение щедрых сумм на сберегательные счета.Даже в ситуациях с ограниченными деньгами вам необходимо откладывать часть своих доходов на сбережения и проложить путь к безопасному будущему. Если вы хотите получить максимальную отдачу от своих сбережений и инвестиций, вложения, предполагающие расчет сложных процентов, могут быть жизнеспособным вариантом. Посмотрите, как работают сложные проценты, и ознакомьтесь с некоторыми примерами сложных процентов в реальной жизни.
Посмотрите, как работают сложные проценты, и ознакомьтесь с некоторыми примерами сложных процентов в реальной жизни.
Формула сложных процентов и пример
Сложные проценты — это один из двух способов расчета процентов, второй — простой процент.nt. Чтобы разбить это, P — исходная сумма денег, i — процентная ставка, n — количество периодов процентных ставок, а t — общее количество лет для ссуды или депозита. Вы можете использовать калькулятор сложных процентов или формулу электронной таблицы, чтобы сэкономить время, по сравнению с вычислением вручную.
Если, например, вы инвестировали 1000 долларов и заработали 50 долларов в виде процентов в конце периода заработка, ваша новая основная сумма станет 1050 долларов . Процентная ставка будет применяться к 1050 долларов, а не к исходному 1 000 долларов, при следующем начислении процентов.
Помогает компаниям получать прибыль
Сложные проценты открывают двери к источникам прибыли для компании. Например, предприятия могут порадовать инвесторов, принося им более высокую прибыль, чем ожидалось. Ожидается, что финансовые менеджеры выплатят инвесторам дивиденды. Если эти дивиденды накапливаются или, точнее, суммируются и реинвестируются в бизнес, в следующем году могут быть выплачены более высокие дивиденды.
По словам Чарльза Шваба, сложные проценты — это средство роста прибыли, если их использовать с умом.Это работает как мультипликатор прибыли, и с каждым годом интерес инвесторов растет, потому что они получают проценты по процентам.
Обеспечение пенсионных выплат
Различные компании обращаются за помощью в открытие инвестиционных счетов для выплаты пенсий. Обычно работодатели исключают фиксированную сумму из заработной платы своих сотрудников и вносят ее в свой пенсионный фонд. Сумма накапливается годами до достижения сотрудниками пенсионного возраста, когда вся сумма выплачивается в виде пенсии.
Сумма накапливается годами до достижения сотрудниками пенсионного возраста, когда вся сумма выплачивается в виде пенсии.
Предприятия используют деньги пенсионных фондов для инвестирования в финансовые инструменты, обеспечивающие гарантированную доходность. Это помогает обеспечить плавный цикл пенсионных выплат и стабильную отдачу от вложений, накопленных за многие годы. Основным принципом пенсионного трастового фонда является своевременная выплата пенсий своим вышедшим на пенсию сотрудникам, процесс, который эффективно подкрепляется концепцией сложных процентов.
Плюсы и минусы сложных процентов
Рассмотрев некоторые примеры сложных процентов в реальной жизни, вы увидите, что идея сложных процентов привлекательна только тогда, когда вы находитесь на прибыльной стороне финансового баланса.Банки обычно выплачивают сложные проценты по депозитам. Итак, это приносит вам пользу, если вы вкладываете деньги.
С другой стороны, если вы являетесь держателем кредитной карты, знание принципов расчета сложных процентов может быть стимулом для быстрой выплаты остатков. Компании, выпускающие кредитные карты, взимают проценты с основной суммы и накопленных процентов. Если вы продлите выплату долга по кредитной карте, ваша основная сумма будет расти, потому что при расчете сложных процентов начальная сумма будет сброшена, чтобы включить ранее заработанные проценты.
Компании, выпускающие кредитные карты, взимают проценты с основной суммы и накопленных процентов. Если вы продлите выплату долга по кредитной карте, ваша основная сумма будет расти, потому что при расчете сложных процентов начальная сумма будет сброшена, чтобы включить ранее заработанные проценты.
Выгода от сложных процентов зависит от вашей финансовой перспективы. Если вы являетесь заемщиком, расчет сложных процентов приводит к увеличению суммы вашей задолженности, и кредитор получает выгоду. Если вы инвестор, вы получаете прибыль по мере роста ваших денег.
Как на самом деле работает сложный процент. Углубленный анализ сложных процентов с примерами из реального мира.
Сложный процент — возможность изменить состояние
Знаете ли вы следующую поговорку:
«Капельки воды делают могучий океан»
Ну, сложный процент — это что-то в этом роде, но на стероидах! На самом деле, по слухам, Альберт Эйнштейн сказал, что «сложные проценты — самая мощная сила во Вселенной».
Учитывая любовь Эйнштейна ко Вселенной и всем ее могущественным силам, похоже, что он хотел, чтобы мы обратили на это внимание.
Но что же такого особенного в сложных процентах? Может ли простая математическая концепция действительно иметь такое влияние на то, как мы занимаем деньги и сберегать, чтобы повлиять на наше финансовое благополучие?
Сложные проценты — это то, что делает нас богатыми и делает нас бедными
Большинство людей знают о финансовых проблемах, в которых Греция оказалась в 2007-2008 годах.Мы также продолжаем слышать о том, что Соединенные Штаты время от времени приближаются к «потолку долга». Это случаи роста долга с годами и достижения такого уровня, который может привести к полной остановке даже богатых и могущественных национальных государств. Долг сам по себе достаточно страшен, но когда вы добавляете к нему сложные проценты, он может стать паразитирующим.
Но это еще не все мрак и гибель. У этого есть обратная сторона. Что, если бы вместо заплатили эту постоянно растущую кучу денег кому-то, а вы вместо заработали бы ? Это обещание, лежащее в основе многих вариантов сбережений, таких как пенсионные планы, сберегательные счета с выплатой процентов и даже некоторые инвестиции, привязанные к фондовому рынку.Прежде чем мы углубимся в это, давайте посмотрим, что же такое сложный процент.
Что, если бы вместо заплатили эту постоянно растущую кучу денег кому-то, а вы вместо заработали бы ? Это обещание, лежащее в основе многих вариантов сбережений, таких как пенсионные планы, сберегательные счета с выплатой процентов и даже некоторые инвестиции, привязанные к фондовому рынку.Прежде чем мы углубимся в это, давайте посмотрим, что же такое сложный процент.
Математика сложных процентов
Математическая формула выглядит просто так:
(подробнее о формуле здесь )
Эта формула может помочь вам рассчитать окончательную сумму с начислением сложных процентов для любой ситуации под солнцем. Разберем его на компоненты или «переменные», как их обычно называют.
A = Это окончательная сумма в конце срока ссуды / инвестиции. Он включает основную сумму, а также сложные проценты, начисленные с течением времени.
P = Это первоначальная сумма основного долга в начале ссуды или инвестиции.
r = Это годовая процентная ставка. Имейте в виду, что 24% означает 0,24, 12% — 0,12 и так далее.
Имейте в виду, что 24% означает 0,24, 12% — 0,12 и так далее.
t = Это общий срок или продолжительность ссуды в годах. Если период меньше одного года, можно использовать дроби.Например, 6 месяцев будут 0,5 года, и вы можете ввести 0,5 в формулу.
n = Количество начисленных процентов за год. Таким образом, в случае ежемесячного начисления сложных процентов это будет 12; в случае ежедневного начисления сложных процентов — 365 и так далее.
Однако большинство людей (включая опытных инвесторов) не используют эту формулу каждый раз. Они просто используют калькулятор или какое-либо программное обеспечение, такое как MS Excel, и вы можете сделать то же самое здесь, .
Как на самом деле работает формула
Логика формулы.
Если вам не нравится смотреть на формулы, вот как это действительно работает .
Предположим, у нас есть заем в размере $ 10 000 $ с годовой процентной ставкой $ 24 \% $ (которая составляет $ 2 \% $ в месяц), которая начисляется каждый месяц.
Эта ссуда эквивалентна получению ссуды на ОДИН месяц с последующим ее пролонгированием еще 11 раз.
Начнем с января месяца.
Проценты за январь = $$ 2 \% $$ от $$ \ $ 10,000 $$ = $$ \ $ 200 $$.
Теперь мы просто добавляем этот процент к первоначальной основной сумме, чтобы получить основную сумму за февраль. Таким образом, наша новая основная сумма за февраль включает исходную основную сумму + проценты за январь = 10 200 долларов США.
Процентная ставка за февраль = 2% от 10 200 долларов США или 204 доллара США.
И основная сумма за март равна = 10 200 долларов США + 204 доллара США = 10 404 долларам США.
Мы можем продолжать делать это для каждого месяца и получить тот же результат, что и при использовании формулы.
| Годовая процентная ставка | 24% | |
| Ежемесячная процентная ставка | 2% | |
| Месяц | Основная сумма | Проценты |
| январь | 10 000 | 200 |
| Февраль | 10 200 90 4 27 | 204 |
| март | 10,404 | 208 |
| Апрель | 10 612 90 4 27 | 212 |
| Май | 10 824 90 4 27 | 216 |
| июнь | 11 041 90 4 27 | 221 |
| июль | 11 262 | 225 |
| август | 11 487 90 4 27 | 230 |
| сентябрь | 11717 | 234 |
| Октябрь | 11 951 | 239 |
| ноябрь | 12,190 | 244 |
| декабрь | 12 434 | 249 |
Простой заем с ежемесячным начислением сложных процентов
Общая сумма на конец декабря составляет основная сумма (12 434 доллара США) + проценты (249 долларов США) = 12 682 доллара США.
Салли и ее кредитные карты
Математика хороша и все такое, но как она работает в реальной жизни? Допустим, у нашей подруги Салли есть ссуда в размере 10 000 долларов США. Допустим, ее банк взимает с нее годовую процентную ставку (APR) в размере 24%. Вот различные примеры:
Пример 1: Простая процентная ставка (без начисления сложных процентов)
В этой ситуации с Салли просто взимается годовая процентная ставка в размере 24% или 2400 долларов США каждый год по ссуде.Ее общая сумма обязательств в конце составляет 12 400 долларов США.
Пример 2: Сложные проценты — начисляются ежемесячно
Годовая ставкаSally составляет 24%, что дает нам 2% в месяц. Мы уже вычислили этот пример в предыдущей таблице и знаем, что результат составляет 12 682 доллара США. Обратите внимание, как эта сумма со сложными процентами выше по сравнению с суммой в Примере простых процентов.
Пример 3: Сложный процент — ежедневное начисление
Но подождите — это может стать еще более напряженным! Если вместо ежемесячного начисления сложных процентов банк будет выполнять ежедневное начисление сложных процентов (что на самом деле делают многие компании, выпускающие кредитные карты!), Ссуда Салли раздулась бы еще быстрее.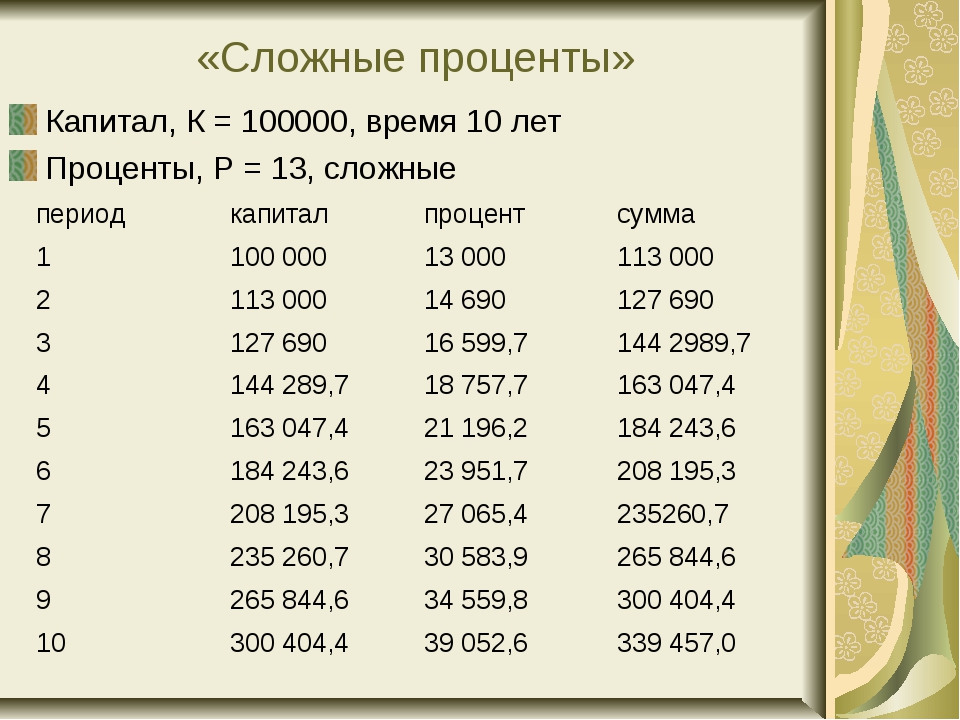 При той же годовой ставке 24% с ежедневным начислением сложных процентов первоначальные 10 000 долларов США к концу года составят 12 711 долларов США.
При той же годовой ставке 24% с ежедневным начислением сложных процентов первоначальные 10 000 долларов США к концу года составят 12 711 долларов США.
Вот что мы получаем из наших трех примеров:
| Простая процентная ставка (без начисления сложных процентов) | Сложные проценты — начисляются ежемесячно | Сложные проценты — начисляются ежедневно | |
| Итого к оплате до декабря | 12 400 долларов США | 12 682 долл. США | 12 711 долларов США |
Итак, вот оно.Несмотря на то, что основная сумма кредита (10 000 долларов США) и процентная ставка (24%) одинаковы, частота начисления сложных процентов может существенно отличаться от общей суммы кредита. Разница может показаться небольшой, но мы сделали расчет только для одного года и для скромного кредита в размере 10 000 долларов США. В течение вашей жизни разница может легко достигать сотен тысяч долларов. Это определенно не то, что вы должны игнорировать.
Заработок на сложных процентах
К счастью, огромная мультипликативная сила сложных процентов может работать и в нашу пользу.Самый простой пример — это простой сберегательный счет. Если вы вложите в него немного денег и забудете об этом — он будет со временем расти, как и процентные выплаты в наших предыдущих примерах ссуд. Однако процентная ставка по сберегательным счетам недостаточно высока, чтобы они могли быть привлекательным вариантом для сбережений.
Здесь на помощь приходят различные варианты инвестирования. Каждый раз, когда вы реинвестируете деньги, полученные от инвестиций, вы в некотором смысле получаете выгоду от начисления сложных процентов.В некоторых случаях вам придется делать это вручную, но многие инвестиционные планы делают это за вас автоматически.
Давайте взглянем на простой пенсионный план с годовой доходностью 7%, начисляемой ежегодно. Для простоты мы предполагаем, что вложение произошло только один раз, а не в качестве повторяющегося.
Салли вложила 10 000 долларов в этот план в 1990 году. Ее подруга Маргарет вложила 20 000 долларов в этот же план в 2005 году. Давайте посмотрим, сколько их портфелей стоит сейчас — в конце 2017 года.
С помощью калькулятора мы видим, что теперь вложение Салли составляет 62 139 долларов США.
Используйте в калькуляторе следующие значения:
P = 10 000 долларов США
г = 0,07 (7%)
t = 27 лет (с 1990 по 2017)
N = 1 (годовое начисление)
Теперь давайте посмотрим, сколько денег заработала Маргарет, которая вложила , вдвое больше, чем Салли, на , но сделала это в 2005 году. Подставляя числа в калькулятор, мы получаем 45 044 доллара.
Это сила начисления процентов. Если вы возьмете счет 401 (k), который не только дает вам преимущество в виде начисления сложных процентов, но также дает экономию налогов и стимул для ежегодных инвестиций — вы можете сэкономить значительную сумму. Фактически, одна из основных причин, по которой правительство предоставляет эти налоговые льготы, заключается в том, что граждане получают дополнительный стимул пользоваться преимуществами этих планов сбережений и обеспечивать свое будущее финансово.
Непрерывное компаундирование
Как мы видели ранее, ежедневная ссуда с начислением сложных процентов растет быстрее, чем ежемесячная ссуда с начислением сложных процентов.Точно так же, если вы производите начисление сложных процентов почасово, ссуда будет расти еще быстрее. В конце концов мы достигаем стадии, когда период начисления сложных процентов настолько мал, что мы рассматриваем его как непрерывно начисляемую ссуду.
Практически невозможно вычислить это вручную, но сила математики дает нам формулу для вычисления того же самого. Вы можете воспользоваться калькулятором по этой ссылке, если вам интересно.
Тем не менее, не стоит слишком беспокоиться об этом, так как влияние этого непрерывного компаундирования невелико.Кроме того, очень немногие ссуды фактически постоянно пополняются. Как уже упоминалось, кредитная карта в основном пополняется только на ежедневной основе.
Защита ваших «интересов»!
Мы увидели силу сложного капитала — как для того, чтобы втягивать в долги немногих небрежных, так и для того, чтобы дать тем, кто имеет привычку откладывать сбережения, удобную и постоянно растущую пенсионную подушку.
Прежде чем брать ссуду (включая кредитную карту!), Убедитесь, что вы полностью осведомлены о точных условиях ссуды.Спросите о процентных ставках, ВСЕХ комиссиях и сборах и частоте начисления сложных процентов. Затем вы можете вставить эти значения в калькулятор и получить точную сумму, которую вы должны. Самая важная вещь, которую следует помнить для вашего финансового благополучия, — это то, что даже небольшая разница в сборах, сборах или процентных ставках может иметь огромное значение со временем, особенно в отношении сложных процентов.
4 способа использования простых процентов в реальной жизни
Простые проценты — это стоимость использования или заимствования денег без сложных процентов или процентов на проценты.Его относительно легко вычислить, поскольку вам нужно основывать его только на основной сумме заимствованных денег и периоде времени.
Простой процент работает в вашу пользу, когда вы заемщик, потому что он удерживает общую сумму, которую вы платите, ниже, чем это было бы со сложными процентами. Однако, когда вы инвестор, это может работать против вас, потому что вы хотите, чтобы ваша прибыль увеличивалась как можно больше, чтобы получить максимальную отдачу от своих инвестиций.
Однако, когда вы инвестор, это может работать против вас, потому что вы хотите, чтобы ваша прибыль увеличивалась как можно больше, чтобы получить максимальную отдачу от своих инвестиций.
Чтобы понять, как это работает, полезно взглянуть на некоторые жизненные ситуации, в которых используется простой процент.
Ключевые выводы
- Простые проценты — это то, чего стоит занять деньги без сложных процентов, то есть проценты по основной сумме и по процентам.
- Простая процентная ставка рассчитывается исходя из основной суммы займа, процентной ставки и периода времени, который она будет покрывать.
- Простые проценты более выгодны для заемщиков, чем сложные проценты, поскольку они позволяют снизить общие процентные выплаты.
- Автокредиты, погашаемые ежемесячно, и кредиты розничным продавцам, также рассчитываемые ежемесячно, являются примерами простых процентов; как сальдо ссуды падает с каждым ежемесячным платежом, так и проценты.

- Депозитные сертификаты (CD) выплачивают определенную сумму процентов в установленную дату, представляющую собой простые проценты.
Автокредит
Автокредиты амортизируются ежемесячно, что означает, что часть кредита идет на выплату непогашенного остатка кредита каждый месяц, а оставшаяся часть идет на выплату процентов.
Поскольку остаток непогашенной ссуды уменьшается каждый месяц, процентная ставка к уплате уменьшается, что означает, что большая часть ежемесячного платежа идет на погашение основной суммы долга.
Например, предположим, что у вас есть автокредит на 20 000 долларов. Ваша процентная ставка составляет 4%. Чтобы найти простой процент, умножаем 20000 × 0,04 × 1 год. Таким образом, при использовании простых процентов 20 000 долл. США под 4% на 5 лет составят (20 000 долл. США * 0,04) = 800 долл. США в виде процентов в год. Общая сумма причитающегося платежа составит 800 долларов США в год * 5 лет + 20 000 долларов США = 24 000 долларов США. Тогда ежемесячная процентная ставка составит 800 долларов США / 12 = 66,67 долларов США. Вы берете общий ежемесячный платеж, который рассчитывается как 24 000 долларов США / 60 месяцев = 400 долларов США платежа в месяц. Таким образом, основной платеж составит 400 — 66 долларов.67 = 333,33 доллара в месяц.
Тогда ежемесячная процентная ставка составит 800 долларов США / 12 = 66,67 долларов США. Вы берете общий ежемесячный платеж, который рассчитывается как 24 000 долларов США / 60 месяцев = 400 долларов США платежа в месяц. Таким образом, основной платеж составит 400 — 66 долларов.67 = 333,33 доллара в месяц.
Заемщики могут воспользоваться скидками, предлагаемыми при досрочном погашении, особенно при выплате простых процентных ссуд.
Прочие потребительские кредиты
Универмаги часто предлагают крупную бытовую технику на простой процентной основе на срок до одного года. Таким образом, если вы покупаете холодильник за 2000 долларов и платите простые проценты по годовой ставке 8% ежемесячными платежами, ваш ежемесячный платеж будет близок к 174 долларам. Это означает, что вы в конечном итоге заплатите 2088 долларов, а общие процентные расходы составят 88 долларов.
Это существенно меньше, чем 160 долларов, которые вы заплатили бы в счет процентных расходов, если бы взяли ссуду в размере 2000 долларов в течение всего года вместо того, чтобы выплачивать ее часть каждый месяц.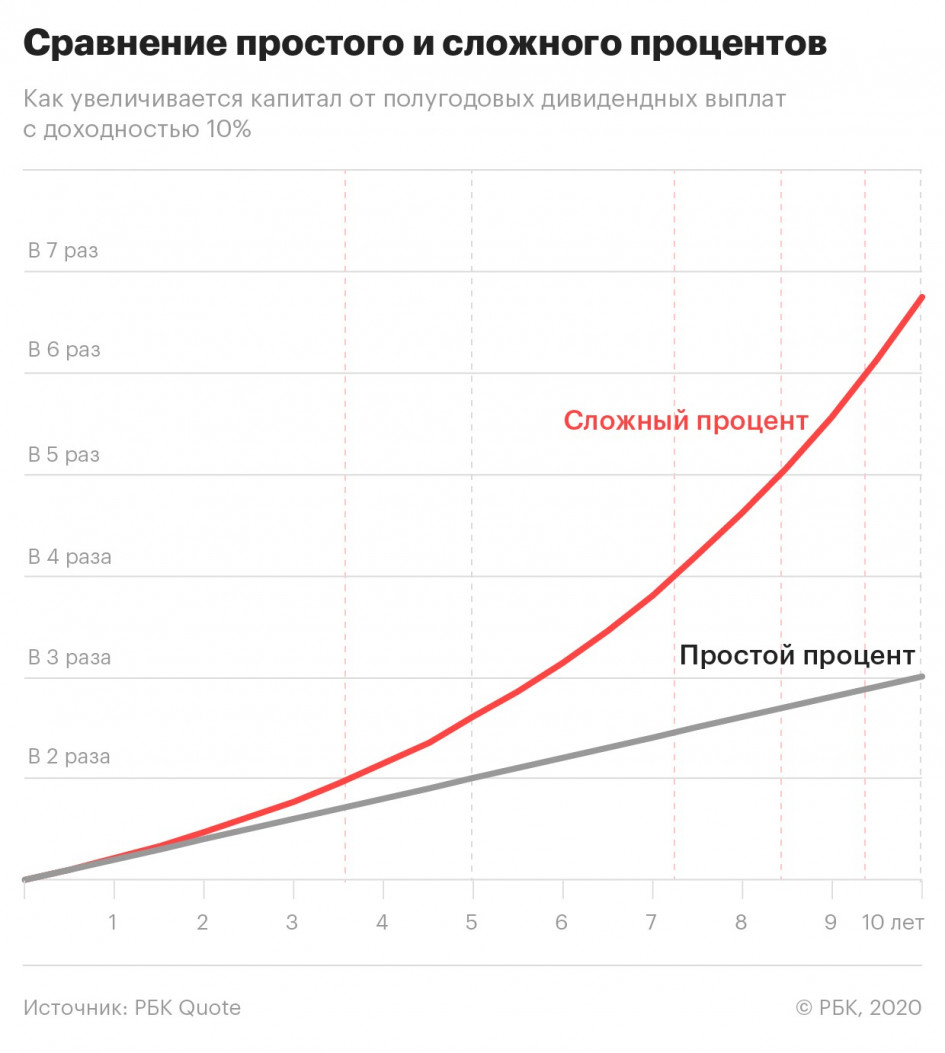
Депозитные сертификаты
Депозитный сертификат (CD) — это вид банковских вложений, по которому выплачивается определенная сумма денег в установленный срок. Вы не можете снять деньги с компакт-диска до наступления установленной даты.
Если вы инвестируете 100000 долларов в однолетний компакт-диск с процентной ставкой 2% годовых, вы получите 2000 долларов в виде процентного дохода (100000 x 0.02 x 1) через год. Если CD выплачивает такую же годовую процентную ставку, но только за шестимесячный период, вы получите 1000 долларов в виде процентного дохода через шесть месяцев (100000 x 0,02 x 0,5).
Скидки на досрочные выплаты
В деловом мире поставщики часто предлагают скидки, чтобы стимулировать досрочную оплату своих счетов.
Например, счет на 50 000 долларов может предлагать скидку 0,5% при оплате в течение месяца. Это составляет 250 долларов за досрочный платеж или 6% годовых, что является довольно привлекательной сделкой для плательщика.
Сложные проценты | Определение и пример
В финансовом мире сложные проценты часто называют магией. Сложные проценты можно рассматривать как «проценты, основанные на процентах», которые увеличивают вашу основную сумму. С точки зрения непрофессионала, это основной способ построить богатство с небольшими усилиями.
Сложные проценты не так волшебны, когда они выплачиваются по ссуде. В этом случае это работает на кредитора — и против вас.
Что такое сложный процент?
Сложные проценты определяются как проценты, полученные на основную сумму долга, плюс проценты, полученные ранее.
Сложные проценты важно понимать, если вы:
Например, когда вы кладете деньги на высокодоходный сберегательный счет и оставляете его там, с этих денег каждый месяц будет взиматься определенная сумма процентов. Банк выплачивает вам проценты за хранение ваших денег. Эти ежемесячные проценты добавляются к вашей основной сумме (первоначальному депозиту), и проценты снова собираются в следующем месяце. Это цикл, в котором проценты приносят проценты, а ваши деньги работают на вас, пока вы спите.
Это цикл, в котором проценты приносят проценты, а ваши деньги работают на вас, пока вы спите.
Как рассчитать сложные проценты
Формула сложного процента:
Если вы не хотите вычислять эту формулу, вы можете найти калькулятор сложных процентов, который выполнит расчет за вас.
Как рассчитать сложный процент в Excel
Существует несколько способов расчета сложного процента в Excel. Быстрый способ — использовать следующую формулу:
A = PV (1 + i) n
A = окончательная сумма
PV = Текущая основная сумма
i = процентная ставка
n = количество периодов начисления сложных процентов ( частота)
Пример сложного процента в Excel
Допустим, у вас есть 10 000 долларов США и процентная ставка 5%.Проценты взимаются каждый месяц, поэтому они увеличиваются ежемесячно. Через три года ваши первоначальные инвестиции в размере 10 000 долларов США вырастут до 11 615 долларов США (если вы их не коснетесь).
Вот пример того, как этот расчет выглядит в Excel:
Формула Excel округляется в большую сторону. Запустив те же цифры в калькуляторе сложных процентов Investor.gov, вы получите ответ с точностью до копейки.
Важность частоты при начислении сложных процентов
В зависимости от банка или типа инвестиций сложный процент может рассчитываться с разной частотой.Обычные частоты — ежедневно, ежемесячно и ежегодно. Чем чаще начисляются сложные проценты, тем быстрее будет расти ваш баланс.
По теме: Как одна нормальная женщина превратила 200 долларов в 7 миллионов долларов
То же самое верно и для ссуды или долга, когда вы не выплачиваете проценты. Чем больше периодов начисления сложных процентов, тем быстрее будет расти ваш причитающийся баланс.
Примеры сложных процентов с использованием частоты
Предположим, у вас есть 100 долларов, чтобы открыть сберегательный счет 1 января. Годовая процентная ставка 5%. Сколько у вас будет через пять лет?
Годовая процентная ставка 5%. Сколько у вас будет через пять лет?
Если начисляются проценты ежегодно
Если банк просто дал вам 5% от ваших 100 долларов в конце года, 31 декабря у вас будет 105 долларов. Если вы оставите 105 долларов на счете, чтобы заработать еще 5% в следующем году, в конце этого второго года у вас будет: 105 долларов x 1,05 = 110,25 доллара.
Вы не только заработали проценты на свои первоначальные 100 долларов во второй год, но и заработали проценты на годовые проценты.Если вы проделаете это еще восемь лет, вот как может выглядеть ваша учетная запись:
По истечении 10 лет у вас на счете будет 162,89 доллара, если вы абсолютно ничего не делаете. Но становится лучше.
If Interest Compounds Monthly
В приведенном выше примере предполагается, что банк выплачивает проценты по остатку в конце года. Банк обычно выплачивает проценты на остаток на вашем счете в конце каждого месяца. Банк делит годовую процентную ставку (5%) на 12 месяцев, а затем применяет эту ставку к вашему балансу в конце каждого месяца.
Банк делит годовую процентную ставку (5%) на 12 месяцев, а затем применяет эту ставку к вашему балансу в конце каждого месяца.
В первый год происходит следующее:
Обратите внимание, что когда банк ежегодно составлял баланс, у вас было только 105 долларов в конце первого года. Но если банк пополняется ежемесячно, в конце первого года у вас будет 105,12 доллара.
Это может показаться не таким уж большим, но рассмотрите влияние на гораздо больший баланс в 500 000 долларов. По истечении 10 лет у инвестора будет 814 447,13 долларов США (при условии, что проценты будут составлять ежегодно). Но у них было бы 823 504,75 доллара — полные 9 057 долларов.Еще 62 — при ежемесячном начислении процентов.
Когда высокая частота начисления сложных процентов не работает для вас
Частота начисления сложных процентов не только влияет на то, сколько процентов вы можете заработать, но и на то, сколько процентов вы платите.
Например, если сберегательный счет на 1000 долларов был ссудой на 1000 долларов, на сумму процентов, которую вы платите, будет влиять частота, с которой ваш банк усугубляет ставку. Важный урок здесь заключается в том, что чем чаще происходит начисление сложных процентов, тем больше процентов зарабатывается (или выплачивается) на баланс.Некоторые кредитные карты даже ежедневно получают сложные проценты, что сильно влияет на задолженность заемщика.
Что такое непрерывные сложные проценты?
Непрерывные сложные проценты — это математический предел формулы сложных процентов. Идея состоит в том, что это усугубляется каждым возможным приращением времени вместо установленных периодов.
Непрерывные сложные проценты — это скорее теория, чем практика, поскольку вы никогда не увидите, чтобы банк или ссуда работали таким образом.
Простые проценты по сравнению со сложными процентами
Простые проценты всегда основываются на основном балансе (первоначальном депозите). Сложные проценты рассчитываются на основе основного баланса и процентов, которые добавляются каждый раз, когда происходит начисление сложных процентов.
Сложные проценты рассчитываются на основе основного баланса и процентов, которые добавляются каждый раз, когда происходит начисление сложных процентов.
Формула для простых процентов:
Ипотека и автокредиты являются примерами, в которых вместо сложных процентов используются простые проценты. (Это затруднило бы когда-либо выплату за дом или машину!)
На что обращать внимание при начислении сложных процентов
Это определение охватывает лишь некоторые из многих методов расчета процентов.Заемщикам следует сравнивать предложения кредиторов, а инвесторам следует сравнивать инвестиционные предложения, внимательно читая раскрываемую информацию. Закон о правде в кредитовании (TILA) призван гарантировать, что компании раскрывают все условия кредита для заемщиков.
Инвесторы должны понимать, как выбор организацией методов расчета процентов может повлиять на сумму процентов, применяемых к их счету. Например, депозитный сертификат (CD) может содержать простые проценты или сложные проценты (сложный процент со временем приведет к увеличению благосостояния инвестора).
Как работают сложные проценты: примеры из жизни
К инвестиционному процессу можно подойти стандартно: получить прибыль, вернуть вложенную сумму и вложить снова или не менять сумму изначально вложенных средств. Однако есть способ увеличить прибыль.
Под сложными процентами считается эффект, когда прибыль добавляется к основной сумме и участвует в создании новой прибыли в будущем.
Сложные проценты — это понятие, которое имеет много значений: это реинвестирование дивидендов, прибавление начисленных процентов к сумме депозита и увеличение инвестиций компаний в свои новые проекты за счет прибыли.
Теперь нас интересует, что касается вложений в ценные бумаги, валюту и другие активы, обращающиеся на бирже. Поэтому нас больше всего интересует понятие «реинвестирование».
Реинвестиции можно разделить по объекту, на который они направлены, по:
Реальные реинвестиции — это вложения прибыли в недвижимость, оборудование и т. Д.реальные активы. Финансовое реинвестирование — это вложение прибыли в фондовый рынок, бинарные опционы, ПАММ-сеты и т.д.
Д.реальные активы. Финансовое реинвестирование — это вложение прибыли в фондовый рынок, бинарные опционы, ПАММ-сеты и т.д.
Богатые люди знают силу сложных процентов и долгосрочных инвестиций.
Если вы нашли интересный прибыльный проект, не спешите снимать с него деньги, пусть сложный процент сделает свое дело. Итак, известный миллиардер Уоррен Баффет никогда не покупает акции менее 10 лет.
Аналитики пришли к мнению, что любой инвестор (даже без большой суммы денег) через полгода реинвестирования прибыли может увеличить свой капитал на 5-15% только за счет сложных процентов.
Критики реинвестирования обращают внимание на риски (компания обанкротится, Управляющий «сольет депозит» и т. Д.), Не рекомендуют «класть яйца в одну корзину», советуют переложить освобожденные средства в другую. актив или потратить на себя.
В этом есть доля правды — фондовые рынки периодически «штурмуют», не все компании стабильны, вокруг много мошенников. Однако это не повод сразу паниковать и фиксировать прибыль, как только она появилась.
Изъятие прибыли из обращения просто для того, чтобы удержать ее, иногда бывает очень дорого. Часто это приводит к тому, что многие годы приходится топтать на одном месте. Хотя сами вложения успешны, инвесторы выводят прибыль, которая затем быстро испаряется.
Реинвестирование — это реинвестирование уже полученной прибыли от актива, то есть ситуация, когда инвестор, получив прибыль от вложения, не забирает ее, а добавляет к ранее вложенным средствам для дальнейшего увеличить доход.
В банках процесс реинвестирования называется капитализацией процентов.
Реинвестиции делятся:
- Снова инвестируется вся прибыль;
- Часть прибыли инвестируется в актив, часть списывается.
Для расчета необходимо взять начальную сумму, умножить ее на процентную ставку, разделенную на 100, в размере, равном периоду, за который производится вложение. Формула выглядит следующим образом:
окончательная сумма = начальная сумма * (1 +%) n
Примером может служить срочный вклад в банке. В реальной жизни при расчете сложных процентов банки используют идеальную формулу, которая имеет вид: конечная сумма равна начальной сумме, умноженной на единицу, плюс процентная ставка, деленная на 100, умноженная на количество дней, разделенное на число. дней в году, возведенных в степень, равную сроку депозита. Таким образом, формула выглядит следующим образом:
В реальной жизни при расчете сложных процентов банки используют идеальную формулу, которая имеет вид: конечная сумма равна начальной сумме, умноженной на единицу, плюс процентная ставка, деленная на 100, умноженная на количество дней, разделенное на число. дней в году, возведенных в степень, равную сроку депозита. Таким образом, формула выглядит следующим образом:
конечная сумма = начальная сумма * (1 + p * d / y) n
Таким образом, если вы вложите 1 000 рублей под 10% годовых , то через год у вас будет 1 100 рублей.Если в следующем году вклад будет увеличен с 1 000 руб., А с 1 100 руб. Вместо 100 руб. Получится руб. 121 Думаю, это немного, но если смотреть в будущее:
- Через 3 года-1 331.
- Через 4 года-1 464.
- Через 10 лет — 2,594.
- Через 20 лет — 6727.
- Через 30 лет-17 449
- Через 40 лет-45 259.
- Через 49 лет — 106719.
- Через 50 лет — 117 391.

Для наглядности следует сравнить результат сложного и простого процентов.Простой процент дает линейное увеличение прибыли, реинвестирование (сложные проценты) дает экспоненциальный рост капитала, что дает больший прирост с большим процентом, большим сроком и большей суммой.
Таким образом, чем больше изначально вложенная сумма, тем дольше она лежит на депозите и чем выше установленная для нее ставка, тем быстрее и сильнее она будет увеличиваться, тем самым еще больше ускоряя процесс роста.
Что делают простые и сложные проценты по ставке 10% годовых на 20 лет.
| Что делают простые и сложные проценты по ставке 10% годовых на 20 лет | ||
| Год | Метод простого процента, руб. | Метод сложных процентов, руб. |
| 1 | 100 000 | 100 000 |
| 2 | 110 000 | 110 000 |
| 3 | 120 000 | 121 000 |
| 4 | 130 000 | 13 300 |
| 5 | 140 000 | 146 410 |
| 6 | 150 000 | 161 051 |
| 7 | 160 000 | 177 156 |
| 8 | 170 000 | 194 872 |
| 9 | 180 000 | 214 359 |
| 10 | 190 000 | 235 795 |
| 11 | 200 000 | 259 374 |
| 12 | 210 000 | 285 312 |
| 13 | 220 000 | 313 843 |
| 14 | 230 000 | 345 227 |
| 15 | 240 000 | 379 750 |
| 16 | 250 000 | 417 725 |
| 17 | 260 000 | 459 497 |
| 18 | 270 000 | 505 447 |
| 19 | 280 000 | 555 991 |
| 20 | 290 000 | 611 591 |
Внимание! ! Для того чтобы сложные проценты полностью раскрыли свой потенциал, требуется время или высокая процентная ставка, что редко бывает в проектах с низким уровнем риска.
Ниже приведен пример того, как вы можете заработать 1000000 долларов в течение 11 лет с первоначальным взносом в размере 3000 долларов США под 50% годовых с ежемесячным пополнением в размере 300 долларов США (т. Е. 3600 долларов США в год).
1 год 8 565 $
2 года $ 17 362
3 года 30,558 $
4 года 50 351 $
5 лет $ 80 042
6 лет $ 124 577
7 лет 191,381 $
8 лет $ 291 586
9 лет 441 893 $
10 лет $ 667 355
11 лет 1 001 032 $
Более подробно этот пример описан в статье о пассивном доходе, там вы можете найти множество способов пассивного инвестирования.
Альберт Эйнштейн назвал сложные проценты величайшим изобретением человечества. Об этом говорится во многих книгах по финансовой тематике. Эти книги любят приводить пример, что если вы кладете 1 доллар на депозит под 20% годовых с капитализацией процентов и ежедневно вносите еще 1 доллар, то через 32 года у вас будет 9000 долларов на миллион5.
Внимание! ! К сожалению, сейчас только мошенники предлагают 20% годовых. В России банки предлагают всего 2 — 3% годовых по вкладам в иностранной валюте.Следовательно, для того, чтобы описанная выше стратегия сработала, потребуется более 200 лет.
Сложные проценты — это мощный инструмент, который при правильной настройке создает деньги из воздуха. Это как «волшебная машинка». Сложные проценты могут использовать все, будь то вкладчики или инвесторы.
Реинвестирование имеет как плюсы, так и минусы. Что выбрать: выводить прибыль или инвестировать обратно, решать вам. Единственное, что вы всегда должны помнить, — это цель, ради которой вы инвестируете. Кроме того, вы должны нести полную ответственность за свои решения и всегда думать о них, прежде чем что-то делать.Мы, в свою очередь, постараемся максимально помочь вам в этом непростом деле — инвестициях.
Есть вопросы? Пишите в комментариях, наши специалисты ответят вам в ближайшее время.

 n) – P». В третьей строке модуля введите «Завершить функцию». Вы создали макрос функции для расчета сложной процентной ставки. Продолжая работу с тем же листом Excel, приведенным выше, введите «Сложный процент» в ячейку A6 и введите «= Сложный_Процент (B1, B2, B3)». Это дает вам значение 276,28 доллара, что согласуется с первыми двумя значениями.
n) – P». В третьей строке модуля введите «Завершить функцию». Вы создали макрос функции для расчета сложной процентной ставки. Продолжая работу с тем же листом Excel, приведенным выше, введите «Сложный процент» в ячейку A6 и введите «= Сложный_Процент (B1, B2, B3)». Это дает вам значение 276,28 доллара, что согласуется с первыми двумя значениями.
 — ~ -, r- * ° -3. В ПД.1 6 = 0,09531, поэтому (0,1) = 1р (0,1 / 0,09531) / 0,09531 = В (1,04920 ) /0.09531 = 0.5036 •
— ~ -, r- * ° -3. В ПД.1 6 = 0,09531, поэтому (0,1) = 1р (0,1 / 0,09531) / 0,09531 = В (1,04920 ) /0.09531 = 0.5036 •
 Таким образом, независимо от того, насколько ваши деньги ценят с течением времени, сумма всегда рассчитывается по первоначальной стоимости или добавляется. Хотя более практичные, простые процентные ставки не используются в реальной жизни. Например, если вы подаете заявку на кредит или вкладываете свои деньги, расчеты всегда выполняются с учетом сложных процентов.
Таким образом, независимо от того, насколько ваши деньги ценят с течением времени, сумма всегда рассчитывается по первоначальной стоимости или добавляется. Хотя более практичные, простые процентные ставки не используются в реальной жизни. Например, если вы подаете заявку на кредит или вкладываете свои деньги, расчеты всегда выполняются с учетом сложных процентов. Вот почему мы говорим, что и для простых процентов, и для сложных процентов требуются три фактора: заемный (или инвестированный) капитал, срок платежа и процентная ставка, подлежащая начислению.
Вот почему мы говорим, что и для простых процентов, и для сложных процентов требуются три фактора: заемный (или инвестированный) капитал, срок платежа и процентная ставка, подлежащая начислению. Уже ячейка B4 представляет собой процентную ставку, установленную в 2% ежемесячно в этом примере. Наконец, член ячейки C4 относится к месячному периоду оплаты, в случае 10 месяцев.
Уже ячейка B4 представляет собой процентную ставку, установленную в 2% ежемесячно в этом примере. Наконец, член ячейки C4 относится к месячному периоду оплаты, в случае 10 месяцев.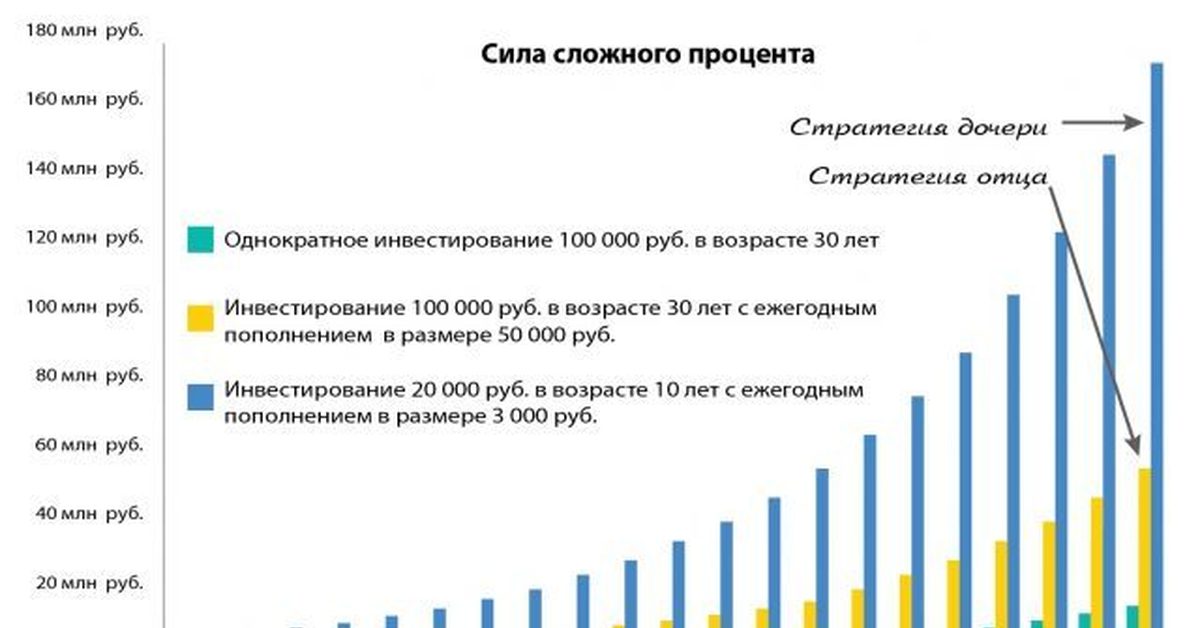 A13
A13 Стоимость ее портфеля после выхода на пенсию составляет 1,5 миллиона долларов. Если она действительно дождется выхода на пенсию в возрасте 60 лет, она сэкономит чуть более 2,5 миллиона долларов.
Стоимость ее портфеля после выхода на пенсию составляет 1,5 миллиона долларов. Если она действительно дождется выхода на пенсию в возрасте 60 лет, она сэкономит чуть более 2,5 миллиона долларов.
