Зависимость давления воды от скорости — Портал о стройке
Фундаментальная ошибка в основе гидродинамики
Источник: http://www.trinitas.ru/rus/doc/0016/001c/00161523.htm
Войцех АКАДЕМИЯ ТРИНИТАРИЗМА
Oб авторе
Существует поразительная возможность
овладеть предметом математически,
не понимая существа дела.
А. Эйнштейн
Аннотация
В статье поднимается важнейший вопрос, и приводятся доказательства ошибочности основополагающего уравнения гидрогазодинамики – «Уравнения Бернулли».
При выводе уравнения были допущены три ошибки:
Первая ошибка была допущена Д.Бернулли из-за незнания особенностей работы жидкостного манометра, который был им применен для измерения давления в потоке жидкости. Он не знал об эффекте эжекции, открытом через 130 лет после написания им формулы, вносящим погрешность в показания жидкостного манометра.
Вторая ошибка была сделана при выводе формулы из-за вольного обращения с расходной массой в потоке, имеющей по условию уравнения расхода заведомо определенную скорость, которая не зависит от изменения сечения трубы. Использование в своем уравнении вместо скорости расхода — скорости потока, зависящей от сечения трубы, привело его к ошибочной мысли о зависимости статического давления от скорости потока.
Третья ошибка была в неадекватности математической модели идеальной жидкости как «Сплошной среды», которая была в основе всей теории.
Принцип, впервые высказанный Даниилом Бернулли в 1726 г., гласит: в струе воды или воздуха давление велико, если скорость мала, и мало, если скорость велика.
Само явление Бернулли, ассоциируемое с изменением давления жидкости или газа в трубопроводе переменного сечения, известно уже 270 лет; давно известно и его физическое толкование. Последнее базируется на представлении, что объемная плотность энергии жидкости или газа, текущих со скоростью V (много меньшей скорости звука в них), обуславливается статическим давлением р и кинетической энергией ρV2 /2 массы единичного объема. В соответствии с этим и с отсутствием подвода к трубопроводу энергии, отмеченное положение математически фиксируется в виде следующей записи:
p + ρV2/2= Ро = coпst, либо (1.а)
p = Ро — ρV2/2, Дж/м3. (1.б)
рис.1 |
Установилось твердое мнение, вошедшее во все учебники физики, что p — это действующее на стенку трубопровода давление жидкости (газа) только вследствие хаотического движения ее частиц, которое уменьшается при увеличении скорости потока в рассматриваемой области. Для доказательства этого «очевидного факта» привлекаются данные эксперимента в виде показаний манометров (рис. 1), подключенных к трубопроводу переменного сечения и якобы показывающих соответствие между изменением действующего давления
Однако это общепринятое мнение находится в серьезном противоречии с законами гидравлики, которым подчиняются и жидкости, и газы, если скорости перемещения их элементарных объемов значительно меньше скорости звука в этих средах.
Ошибка 1.
Рассчитаем внутреннюю кинетическую энергию хаотического движения молекул воды определяющую давление при нормальных условиях. Исходя из средней поступательной скорости хаотического движения молекул воды около 2250 м/сек.,
Рст ~ 2Ек внутр/3. = 2Мνср 2 /3 = 2*1000*5062500/3 = 3375000000 дж/м3.
Если эту энергию сравнить с энергией движения потока воды со скоростью 20 м/сек,
Ек потока ~ Мu2/2 = 1000*400/2 = 200000 дж/м3, то отношение кинетической энергии потока к внутренней кинетической энергии поступательного движения молекул – 1/16800. Даже такая грубая прикидка заставляет задуматься.
Это значит, что изменение скорости потока на 20м/сек. не может значительно отразиться на внутренней энергии объема газа или жидкости, даже если считать, что вся кинетическая энергия поступательного движения жидкости вычитается из внутренней кинетической энергии хаотического движения молекул. Поэтому, исключительно трудно было бы зарегистрировать в эксперименте изменение Рст. при скоростях потока в 10-100 м/сек из-за чрезвычайно малой величины этой энергии относительно внутренней энергии объема газа или жидкости и отсутствия необходимых телеметрических микроманометров с погрешностью менее 0,001% даже в наше время.
Попробуем разобраться.
Вернемся к формуле. p + ρu2/2= Ро = coпst
рис.2 |
Давление p — это статическое давление, которое зарегистрирует манометр, находящийся в жидкости и движущийся вместе с нею – но, это — предположение, домысел современного толкователя формулы, а в действительности, Бернулли, по техническим причинам, не мог провести такой эксперимент, не было в то время прецизионных микроманометров с ошибкой 0,001% и телеметрической системой регистрации, а использовали обычный жидкостной манометр, но,
Но, что же тогда измеряет манометр? Он измеряет силу, уравновешивающую
столб жидкости в манометре Fман. = ρжghм;
которая уравновешивается Pвх.ман. = pст – Fэ ; где:
ρж – плотность жидкости в манометрической трубке;
g – ускорение свободного падения;
hм – высота столба жидкости в манометрической трубке;
pст –статическое давление в жидкости;
Fэ – сила эжекции, возникающая при взаимодействии движущегося потока и входного устройства манометрической трубки, пропорциональна квадрату скорости потока
Fэ ~ u2 и имеет отрицательный знак.
u – скорость движения жидкости;
ρ – плотность жидкости в потоке.
К сожалению, Д.Бернулли не знал о явлении эжекции.
Эжектор был изобретен во Франции инженером Анри Жиффаром в 1858 г, спустя 120 лет после публикации формулы Бернулли. Выходит, что Бернулли написал свою формулу, опираясь на показания измерительного прибора, который измерял совсем не статическое давление в потоке, а сумму статического давления и интенсивности эжекции.
Вывод: а) Д.Бернулли при проведении своих экспериментов был введен в заблуждение показаниями жидкостного манометра, который в принципе не может измерять статическое давление в потоке газа и жидкости. Показания манометра в значительной мере зависели от эжекции потоком жидкости из отвода манометра, поэтому, при измерении «давления» в секциях трубопровода с разным сечением, а, следовательно, и разной скоростью течения, манометр отображал изменение показаний в зависимости от интенсивности эжекции.
Та кривая Р (см. Рис.1), которую интерпретировали как изменение статического давления в потоке в зависимости от скорости потока, на самом деле есть отображение изменения интенсивности эжекции жидкости или воздуха из патрубка манометра в зависимости от скорости течения потока.
Вывод: б) Приближенный расчет соотношения энергии движения потока воды по трубе и внутренней энергии этого объема воды показывает, что если изменение давления и происходит, то его величину практически нельзя обнаружить даже в наше время с использованием самых современных измерительных приборов, что полностью исключает возможность измерения изменения статического давления в потоке жидкости при помощи примитивного жидкостного манометра.
К сожалению, ошибка Д.Бернулли в анализе результатов эксперимента с трубами переменного сечения, убедив его в уменьшении статического давления в потоке, повлекла за собой следующую ошибку, теперь при выводе формулы.
Ошибка 2.
Необходимо признать, что утверждение mν2/2+
Энергия объема V жидкости в любой точке — сумма его кинетической энергии mν2/2 и его потенциальной энергии pV. Эффектами тяготения и вязкости пренебрегают. Энергия данного объема жидкости, которая перемещается от положения 1, до положения 2 – одинаковая в обоих положения. Связанное уравнение энергии:
p1V + mu12/2 = p2V + mu22/2 (1)
Используем подстановку m = ρV, делим обе части уравнения на V, и получаем
Закон Бернулли: p1 — p2 = (ρ/2)(u22 — u12) (2)
рис.3 |
С точки зрения математики, все безупречно, но мы ошибаемся в математической интерпретации физического процесса. Избавившись от массы жидкости и сократив все на объем, мы потеряли физику процесса. Что же все-таки движется по трубе, и с какой скоростью?
Если бы это был идеальный, сухой, мелкий песок, песчинки которого бесконечно малы и скользки, тогда все было бы правильно, но по трубе течет идеальная жидкость, не имеющая внутреннего трения и вязкости, не сжимаемая, как бесконечно твердое тело, но и не имеющая жесткой кристаллической решетки, то есть не имеющей формы.
Это многое меняет.
Вернемся к нашему трубопроводу с переменным сечением.
По законам гидравлики, через сечения S1 и S2 за единицу времени проходит один и тот же объем жидкости Q = Vt = S1lt1 = S2lt2 = S1u1 = S2u2 = const
и одна и та же масса жидкости. G = mt = ρVt = ρS1u1 = ρS2u2= const;
Так как секундный расход определен и равен определена секундная масса = mt,
а, учитывая условие неразрывности потока,
скорость движения центра масс жидкости равна:, в любом сечении трубы !
следовательно – удельная кинетическая энергия потока равная mtνm2/2 = coпst,
независимо от размера сечения Si трубки тока!
В свете всего сказанного, полученное уравнение состоит из одних констант, так как:
mν= const — Закон сохранения импульса тела, а значит и:
mν2/2 = const — Закон сохранения кинетической энергии движущейся массы,
поэтому, так как: mν2/2+ РV = РоV = coпst, где mν2/2 = const и V = coпst;
получаем, что: РV = РоV — mν2/2 = const,
понятно, что, поделив все выражение на V= coпst,
мы получаем: Р = coпst!!!
Закон Паскаля (распределение давления в сообщающихся сосудах)
Не менее важным соображением является то, что при установившемся течении идеальной жидкости, то есть жидкости, не сжимаемой, не обладающей вязкостью и внутренними потерями на трение, разность давлений между входом и выходом трубы должна быть равна нулю, так как если жидкость несжимаемая, то скорость распространения волны давления стремится к бесконечности, а время выравнивания давления в объеме жидкости стремится к нулю и не зависит от скорости течения, значит :
ΔР = Р1 — Р2 = 0. или Р2 = Р1 = const.
В противном случае, течение не будет установившимся и масса жидкости должна испытывать непрерывное ускорение. С другой стороны, в несжимаемой жидкости нельзя, по определению, изменить внутреннее давление, так как она не может быть сжата.
Вывод: в) Показания манометров не отображали статическое давление в потоке, статическое давление не зависит от скорости потока, а уравнение Бернулли не имеет общепринятого смысла.
Ошибка 3.
После неожиданного вывода, что статическое давление в жидкости, движущейся по трубам не зависит от их диаметра, а, следовательно, от скорости течения, возникает вопрос: «Как же быть с изменением скорости течения при изменении сечения трубы? Что является побудительной причиной изменения скорости, если статическое давление не меняется?» Изменение скорости течения – это внутренний процесс, обеспечивающий постоянные объем и давление в текущей жидкости, определяемые расходом, локальным сечением трубы и не требующий никаких дополнительных причин. Средняя скорость молекул в воде при нормальной температуре превышают 2200 м/сек. и изменение сечения трубы, приводящее к ускорению течения потока в трубе на 10-50 м/сек, не сопровождается локальными изменениями давления, — это последствия высокой скорости движения молекул и их взаимодействия. Важно учесть, что перемещение массы воды по трубе – групповое движение всей массы жидкости относительно трубы, инициированное разностью давлений на концах трубы, не изменяет внутренней энергии хаотического движения молекул, от которого и зависит давление в жидкости. Это становится понятным, если сравнить движение жидкости и движение твердого тела. И твердое тело, и жидкость – несжимаемы – они имеют очень плотную упаковку атомов и молекул, и, следовательно, изменить внутреннее давление в обоих случаях, можно только сжав тело внешними силами и деформировав его кристаллическую решетку, простое пространственное перемещение тела не приведет изменению внутреннего давления. Следовательно, совершенно не имеет значение для статического давления, с какой скоростью жидкость движется относительно трубы. Движение непрерывно взаимодействующих молекул, из которых состоит жидкость, определяет равномерное распределение внутренней энергии давления во всем объеме жидкости. Жидкость и газ – это активные среды, а не мертвый набор масс типа песка! Применение к жидкости законов механики твердого тела без учета того, что жидкость состоит не из неподвижных частиц, а из молекул, хаотически движущихся с очень высокими скоростями и непрерывно взаимодействующими друг с другом, привело к теории сплошной среды Эйлера, принесшей с собой кучу необъяснимых «парадоксов». Удивительно, что уравнение Бернулли, нарушая все законы гидродинамики, почти три столетия спокойно принимается научным сообществом, хотя для практики оно не годится, а ученые всего мира пишут все новые и новые книги, не задумываясь, повторяя давно устаревшие ошибочные формулы. Пора осознать примитивность и ошибочность этой теории и перейти на новый уровень понимания процессов в жидкостях и газах. Необходимо создать новую теорию гидрогазодинамики, более соответствующую реальной природе. Начало этому уже положено.
Тем не менее, уравнение Бернулли уже более 270 лет без каких-либо изменений и оговорок продолжает применяться к реальной жидкости, к нестационарным и турбулентным потокам и бездоказательно преподается практически во всех школах, средних и высших технических учебных заведениях, вводя всех в заблуждение, внося непоправимый вред в продвижение и развитие научного и технического прогресса.
Вот это и есть «Великий парадокс».
Особо необходимо подчеркнуть, что, по вышеизложенным причинам, привлечение уравнения Бернулли для объяснения появления сил при обтекании крыла ЛА или аэродинамического элемента ВЭС, принципиально неприемлемо и вредно.
Для объяснения физики аэродинамических сил на крыле, автором разработана новая, «эжекционная теория подъемной силы» [4], использующая эффект эжекции и эффект Коанда и предложен проект “Крылья России». [5]
Литература
1. Загузов И.С., Поляков К.А. Математические модели в аэрогидромеханике. Ч.1: Учебное пособие. Самара: Изд-во «Самарский университет», 2001. 92 с. ISBN 5-86465-228-8
2.БСЭ, Соколов Е. Я., Зингер Н. М., Струйные аппараты, 2 изд., М., 1970;
3.Губин М. Ф., Горностаев Ю. Н., Любицкий К. А., Применение эжекторов на гидроэлектростанциях, М., 1971.
4.Войцех О.Г. Эжекционная модель образования подъемной силы на крыле ЛА, журнал «Интеграл» №2,2009.
5.Войцех О.Г. Национальный проект «Крылья России» // «Академия Тринитаризма», М., Эл № 77-6567, публ.15242, 19.04.2009
http://www.trinitas.ru/rus/doc/0016/001c/00161504.htm
О.Г. Войцех, Фундаментальная ошибка в основе гидродинамики // «Академия Тринитаризма», М., Эл № 77-6567, публ.15449, 03.08.2009
Source: www.skibr.ru
Читайте также
Давление в жидкости. Закон Паскаля. Зависимость давления в жидкости от глубины
В чем причина такого эффекта? Дело в том, что при смещении различных слоев жидкости относительно друг друга в ней не возникает никаких сил, связанных с деформацией. Нет сдвигов и деформаций в жидких и газообразных средах, в твердых же телах при попытке сдвинуть один слой против другого возникают значительные силы упругости. Поэтому говорят, что жидкость стремится заполнить нижнюю часть того объема, в котором она помещается. Газ же стремится заполнить весь объем, в который его помещают. Но это в действительности заблуждение, так как, если посмотреть на нашу Землю со стороны, мы увидим, что газ (земная атмосфера) опускается вниз и стремится заполнить некоторую область на поверхности Земли. Верхняя граница этой области достаточно ровная и гладкая, как и поверхность жидкости, заполняющей моря, океаны, озера. Все дело в том, что плотность газа значительно меньше плотности жидкости, поэтому, если бы газ был очень плотным, он точно так же опускался бы вниз и мы видели верхнюю границу атмосферы. В связи с тем, что в жидкости и газе не возникает сдвигов и деформаций – все силы взаимодействуют между различными областями жидкой и газообразной среды, это силы, направленные по нормальной поверхности, разделяющей эти части. Такие силы, направленные всегда по нормальной поверхности, называются силами давления. Если мы разделим величину силы давления на некоторую поверхность на площадь этой поверхности, мы получим плотность силы давления, которую называют просто давление (или иногда добавляют гидростатическое давление), даже в газообразной среде, поскольку с точки зрения давления газообразная среда практически ничем не отличается от жидкой среды.
Свойства распределения давления в жидких и газообразных средах исследовались еще с начала XVII века, первым, кто установил законы распределения давления в жидкой и газообразной средах был французский математик Блез Паскаль.
Величина давления не зависит от направления нормали к той поверхности, на которой оказывается это давление, то есть распределение давления изотропно (одинаково) по всем направлениям.
Этот закон был установлен экспериментально. Предположим, что в некоторой жидкости существует прямоугольная призма, один из катетов которой расположен вертикально, а второй – горизонтально. Давление на вертикальную стенку будет равно Р2, давление на горизонтальную стенку будет Р3, давление на произвольную стенку будет Р1. Три стороны образуют прямоугольный треугольник, силы давления, действующие на эти стороны, направлены по нормали к этим поверхностям. Поскольку выделенный объем находится в состоянии равновесия, покоя, никуда не движется, следовательно, сумма сил, на него действующих, равна нулю. Сила, действующая по нормали к гипотенузе, пропорциональна площади поверхности, то есть равна давлению, умноженному на площадь поверхности. Силы, действующие на вертикальную и горизонтальную стенки, так же пропорциональны величинам площадей этих поверхностей и так же направлены перпендикулярно. То есть сила, действующая на вертикаль, направлена по горизонтали, а сила, действующая на горизонталь, направлена по вертикали. Эти три силы в сумме равны нулю, следовательно, они образуют треугольник, который полностью подобен данному треугольнику.
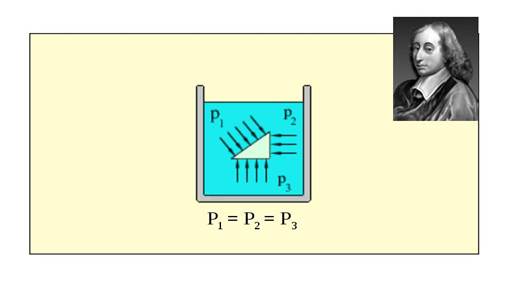
Рис. 1. Распределение сил, действующих на предмет
В силу подобия этих треугольников, а они подобны, так как образующие их стороны перпендикулярны друг другу, следует, что коэффициент пропорциональности между площадями сторон этого треугольника должен быть для всех сторон одним и тем же, то есть Р1 = Р2 = Р3.
Таким образом, мы подтверждаем экспериментальный закон Паскаля, утверждающий, что давление направлено в любую сторону и одинаково по величине. Итак, мы установили, что по закону Паскаля давление в данной точке жидкости одинаково по всем направлениям.
Теперь докажем, что давление на одном уровне в жидкости везде одинаково.
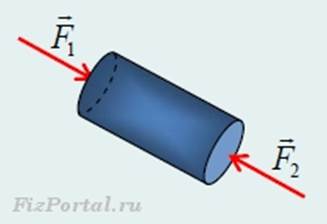
Рис. 2. Силы, действующие на стенки цилиндра
Представим, что у нас есть цилиндр, наполненный жидкостью с плотностью ρ, давление на стенки цилиндра соответственно Р1 и Р2 , поскольку масса жидкости находится в состоянии покоя, то силы, действующие на стенки цилиндра, будут равны, так как и площади у них равны, то есть Р1 = Р2. Вот так мы доказали, что в жидкости на одном уровне давление одно и то же.
Рассмотрим жидкость, находящуюся в поле тяжести. Поле тяжести действует на жидкость и пытается ее сжать, но жидкость очень слабо сжимается, так как она не сжимаема и при любом воздействии плотность жидкости всегда одна и та же. В этом серьезное отличие жидкости от газа, поэтому формулы, которые мы рассмотрим, относятся к несжимаемой жидкости и не применимы в газовой среде.
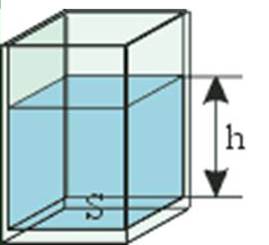
Рис. 3. Предмет с жидкостью
Рассмотрим предмет с жидкостью площадью S = 1, высотою h, плотностью жидкости ρ, который находится в поле тяжести с ускорением свободного падения g. Сверху давление жидкости Р0 и снизу давление Рh , так как предмет находится в состоянии равновесия, то сумма сил, на него действующих, будет равна нулю. Сила тяжести будет равна плотности жидкости на ускорение свободного падения и на объем Fт = ρ g V, так как V = h S, а S = 1, то у нас получится Fт = ρ g h.
Суммарная сила давления равна разности давлений, умноженной на площадь поперечного сечения, но так как у нас она равна единице, то P = Рh — Р0
Так как этот предмет у нас не движется, то эти две силы равны друг другу Fт = P.
Мы получаем зависимость давления жидкости от глубины или закон гидростатического давления. Давление на глубине h отличается от давления на нулевой глубине на величину ρ g h: Рh = Р0 + ( ρ g h ).
Используя два выведенных утверждения, мы можем вывести еще один закон – закон сообщающихся сосудов.

Рис. 4. Сообщающиеся сосуды
Два цилиндра различного сечения соединены между собой, нальем жидкость плотностью ρ в эти сосуды. Закон сообщающихся сосудов утверждает: уровни в этих сосудах будут абсолютно одинаковы. Докажем это утверждение.
Давление сверху меньшего сосуда Р0 будет меньше давления на дне сосуда на величину ρ g h, точно так же давление Р0 будет меньше давления на дне и у большего сосуда на такую же величину ρ g h, так как плотность и глубина у них одинаковы, следовательно, эти величины у них будут одинаковы.
Если же в сосуды налить жидкости с разными плотностями, то уровни у них будут различны.
Законы гидростатики были установлены Паскалем еще в начале XVII века, и с тех пор на основе этих законов работает огромное количество самых разных гидравлических машин и механизмов. Мы рассмотрим устройство, которое носит название гидравлический пресс.
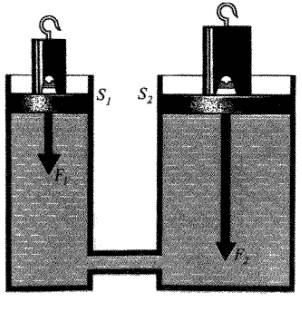
Рис. 5. Гидравлический пресс
В сосуде, состоящем из двух цилиндров, с площадью сечения S1 и S2 налитая жидкость устанавливается на одной высоте. Поставив поршни в эти цилиндры и приложив силу F1, получим F1 = Р0 S1.
Приложив силу F2, получим F2 = Р0 S2.
Из-за того, что давления, приложенные к поршням, одинаковы, легко увидеть, что сила, которую необходимо приложить к большому поршню, чтобы удержать его в покое, будет превышать силу, которая приложена к малому поршню, коэффициент отношения этих сил есть площадь большого поршня делить на площадь малого поршня.
S2
F2 = F1 ̶
S1
Прикладывая сколь угодно малое усилие к малому поршню, мы разовьем очень большое усилие на большем поршне – именно таким образом и работает гидравлический пресс. Усилие, которое будет приложено к большему прессу или к детали, помещенной в то место, будет сколь угодно большим.
Следующая тема – законы Архимеда для неподвижных тел.
Домашнее задание
- Дать определение закону Паскаля.
- Что утверждает закон сообщающихся сосудов.
- Ответить на вопросы сайта (Источник).
Список рекомендованной литературы
- Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Илекса, 2005.
- Громов С.В., Родина Н.А. Физика 7 класс, 2002.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Fiz.1september.ru (Источник).
- 3ys.ru (Источник).
- Fizmat.by (Источник).
- Nika-fizika.narod.ru (Источник).
Зависимость расхода от давления и диаметра. Как вычислить давление в трубе
Последние:- Куда поехать зимой в россии
- Рецепты алкогольных коктейлей для домашней вечеринки
- Как засушить яблоки в домашних условиях?
- Какие программы я устанавливаю на новый компьютер
- Кратчайший пересказ «Алые паруса
Давление в системе отопления в частном доме
Значение давления в системе отопления частного дома
В системе отопления одним из самых важных показателей является именно давление. Оно влияет на качество работы оборудования и определяет, насколько эффективна теплопередача.

Только в том случае, если показатели силы, с которой давит вода, соответствуют норме, можно говорить о качественной работе теплосети. Скорость воды зависит от уровня давления. Чем оно выше, тем быстрее движется поток, и, соответственно, эффективнее теплопередача. Высокий показатель гарантирует доставку воды во все помещения с минимальными потерями температуры.
Если напор будет недостаточно сильный, нагретая в котле вода будет слишком медленно перемещаться по элементам отопительной системы, что приведет к поступлению ее в жилые помещения с температурой намного ниже, чем на выходе из котла. Низкое давление приводит к значительным теплопотерям.
Давление в теплосети бывает двух видов, статическое и динамическое. В первом случае речь идет о силе, с которой столб воды, находящейся в состоянии покоя, давит на котел, трубопровод и радиатор. Зависит этот показатель от высоты. С каждыми 10 метрами он увеличивается на 1 Атм. Под динамическим давлением подразумевается сила, прилагаемая к элементам системы жидкостью, которая движется.
Сумма показателей статического и динамического давления определяет, насколько эффективна система, и носит название рабочего давления.
Как температура носителя влияет на давление
Общеизвестно, что в соответствии с законами физики вещество при нагреве расширяется. Соответственно, при повышении температуры теплоносителя, находящегося в замкнутом пространстве теплосети, увеличивается сила, с которой жидкость давит на ее элементы.
После установки оборудования в систему закачивается жидкость. Так как она холодная, давление минимальное. Путем изменения температуры теплоносителя корригируется давление в сети.
Норма
Для автономной отопительной системы частного дома нормальным считается давление от 0,7 до двух атмосфер.
Конкретная величина рассчитывается еще при проектировании в зависимости от характеристик оборудования, особенностей теплосети, количества этажей. Показатель выше двух атмосфер считается критическим. Если давление достигнет трех атмосфер, произойдет авария. Соединения станут негерметичными, система выйдет из строя.
Обязательным условием, которое дает основание считать давление нормальным, является необходимая разница между показателями в прямой и обратной трубах. Она должна составлять от 0,3 до 0,5 атмосфер.
Причины роста и падения в системе

Перепады давления сигнализируют о проблемах в теплосети.
Если напор снизился, проверить причину можно следующим способом. Нужно остановить насос и проверить, достаточен ли напор статичной жидкости. Если он не упал, значит, проблема в насосах, которые недостаточно сильно толкают теплоноситель.
В том случае, если статическое давление тоже падает, скорее всего, в трубах или котле возникла утечка. В котле могли возникнуть микротрещины.
Их необходимо запаять. Накипь и поломка расширительного бачка также могут вызвать падение напора. Предотвратить образование накипи можно при помощи специальных добавок. Определить место, где нарушилась герметичность, можно путем поочередного отключения элементов теплосети. Если напор нормализуется, значит, утечка именно в отключенной зоне. Внимательный осмотр системы также может помочь выявить место разгерметизации.
Наличие пятен, капель, луж, ржавчины говорят об утечках воды. Чаще всего такого рода проблемы возникают в местах соединения элементов оборудования. Если трубы не стальные, найти следы на месте, где просочилась вода, очень сложно. В этом случае, а также если трубы скрытые, лучше обратиться к специалисту. Он спустит жидкость, при помощи воздуха обнаружит утечку и устранит проблему.
Увеличение давления случается реже и является, как правило, следствием остановки движения теплоносителя. В трех случаях из четырех проблема в регуляторе. Он с целью снизить температуру носителя может закрыть клапаны, прекратив его подачу. Еще одна возможная причина – ошибочная непрерывная подпитка. Такая неисправность может быть как автоматической, так и вызванной чьим-то небрежным вмешательством.
При нормальной работе техники повышение напора может быть вызвано перекрытием задвижки или крана. Причиной увеличения напора теплоносителя может быть также воздушная пробка, закупоривание фильтра или грязевика.
Следует также контролировать изменение разницы напора жидкости между подающей и обратной трубами. Если эта разница возросла, значит, замедлилась циркуляция теплоносителя. И в этом случае возможной причиной может быть воздушная пробка.
Если разница в давлении между трубами приближается к нулю, проблема связана с нарушением движения жидкости или возникла неисправность регулятора отопления.
Как исправить ситуацию

При обнаружении повышения или снижения напора жидкости, прежде всего, необходимо определить, выходят ли отклонения за границы нормы. Если стрелка на манометре находится в зеленой зоне, все в порядке, в белой зоне – давление занижено, а в красной – завышено. Большинство отклонений можно устранить самостоятельно.
Система оснащена двумя клапанами. Один служит для нагнетания теплоносителя, то есть повышения напора, а второй имеет обратное действие и нужен для стравливания жидкости. Прежде всего, стоит воспользоваться одним из этих клапанов в зависимости от типа проблемы. При этом если нужно уменьшить напор теплоносителя, понадобится емкость, в которую будет сливаться лишняя вода.
Для нормализации напора жидкости в каждой закрытой теплосети должен устанавливаться расширительный бак. Это непроницаемая конструкция из стали, состоящая из двух емкостей, одна из которых подключена к системе отопления, а вторая содержит воздух. Разделяет камеры между собой резиновая мембрана, которая при повышении напора смещается в сторону емкости с воздухом, уменьшая тем самым натиск воды.
Более эффективно бороться с перепадами давления можно, если установить предохранительный клапан, воздухоотводчик и манометр. Выполняя каждый свою функцию, эти приборы совместно дают гарантию надежной работы системы.
Манометр демонстрирует, нет ли отклонений от нормы. Воздухоотводчик предотвращает появление воздушных пробок.
Предохранительный клапан при достижении предельных показателей напора воды удаляет из системы ее излишки, направляя их в канализацию или специальный резервуар.
Кроме выше перечисленных методов стабилизации теплосети, существуют приборы, которые полностью автоматизируют контроль и настройку всех параметров системы. Но они имеют высокую стоимость, что делает целесообразность их покупки для установки в частном доме сомнительной.
Расчет – пример
Отклонения в напоре теплоносителя как в меньшую, так и в большую сторону, могут иметь плачевные последствия. Слишком низкие показатели вызывают кавитацию, то есть кипение воды, поломку насоса. Слишком сильный напор жидкости приводит к разрушению системы.
Чтобы избежать этого, необходимо правильно спроектировать теплосеть, подобрать оборудование и смонтировать. Нужно рассчитать, каким количеством жидкости должна быть заполнена система, чтобы напор был в норме. Этот показатель зависит от мощности котла. 13 литров воды приходится на каждый киловатт мощности.
Расчет для разных котлов.
- 10 киловатт мощности – 130 литров воды.
- 16 киловатт – 210 литров.
- 20 киловатт – 260 литров.
Для расчета системы отопления можно воспользоваться одним из соответствующих онлайн-сервисов или программным обеспечением.
Определение требуемого напора воды производится по такой формуле:H = R х L х Zr, где
H – необходимый напор,
R – сопротивление прямого участка трубы (для одноэтажного дома – 150 Па/м),
L – общая длина трубопровода,
Zr – поправочный коэффициент на повышение сопротивления (1,3 – при шаровых кранах и стандартных фитингах, 1,7 – при наличии термостатических регуляторов).
Для примера, сделаем расчет напора воды при длине труб 80 метров и обычных шаровых кранах. Формула в этом случае будет выглядеть так.
H = 150 х 80 х 1,3 = 15600 Па.
Эти данные необходимо учитывать при выборе насоса. Поскольку в технической документации напор указывается в метрах водяного столба, нужно произвести перевод полученного показателя. Один метр водяного столба равен 10000 Па.
Соответственно, 15600 Па – это 1,56 метра.