Разность D=S-P называют дисконтом.

         Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле

,                                                                  (39)

где    d_сл — сложная годовая учетная ставка.

         Дисконт в этом случае равен

.                                (40)

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

 Номинальная и эффективная учетные ставки процентов

Номинальная учетная ставка. В тех случаях, когда дисконтирование применяют m раз в году, используют номинальную учетную ставку f. Тогда в каждом периоде, равном 1/m части года, дисконтирование осуществляется по сложной учетной ставке f/m. Процесс дисконтирования по этой сложной учетнойm раз в году описывается формулой

,                                                                (41)

где N — общее число периодов дисконтирования (N=mn).

         Дисконтирование не один, а  m  раз в году быстрее снижает величину дисконта.

         Эффективная учетная ставка. Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную (по финансовым результатам) номинальной, применяемой при заданном числе дисконтирований в году m.

         В соответствии с определением эффективной учетной ставки найдем ее связь с номинальной из равенства дисконтных множителей

,

 из которого следует, что

.                                                             (42)

Отметим, что эффективная учетная ставка всегда меньше номинальной.

 Наращение по сложной учетной ставке. Наращение является обратной задачей для учетных ставок. Формулы наращения по сложным учетным ставкам можно получить, разрешая соответствующие формулы для дисконтирования (39 и 41) относительно S. Получаем

Из

,                                                     (43)

а из

.                                                 (44)

         2.2 Непрерывные проценты

 Наращение и дисконтирование

Наращенная сумма при дискретных процентах определяется по формуле

,

 где j - номинальная ставка процентов, а m — число периодов начисления процентов в году.

         Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m®¥ имеем

.                                  (45)

Известно, что  

 ^j,

         ^{m®¥                      m®¥}    

где e — основание натуральных логарифмов.

Используя этот предел в выражении (45), окончательно получаем, что наращенная сумма в случае непрерывного начисления процентов по ставкеj равна

.                                                                         (46)

 Для того, чтобы отличать ставку непрерывных процентов от ставок дискретных процентов, ее называют силой роста и обозначают символом d. Тогда

.                                                                         (47)

 Сила ростаd представляет собой номинальную ставку процентов при m®¥.

Дисконтирование на основе непрерывных процентных ставок осуществляется по формуле

.                                                                                 (48)

 Связь дискретных и непрерывных  процентных ставок

         Дискретные и непрерывные процентные ставки находятся в функциональной зависимости, благодаря которой можно осуществлять переход от расчета непрерывных процентов к дискретным и наоборот. Формулу эквивалентного перехода от одних ставок к другим можно получить путем приравнивания соответствующих множителей наращения

.                                                          (49)

          Из записанного равенства следует, что

,                                                 (50)

                          .                           (51)

Расчет срока ссуды и процентных ставок

         В ряде практических задач начальная (P) и конечная (S) суммы заданы контрактом, и требуется определить  либо срок платежа, либо процентную ставку, которая в данном случае может служить мерой сравнения с рыночными показателями и характеристикой доходности операции для кредитора. Указанные величины нетрудно найти из исходных формул наращения или дисконтирования. По сути дела, в обоих случаях решается в известном смысле обратная задача.

Срок ссуды

         При разработке параметров соглашения и оценивании сроков достижения желательного результата требуется определить продолжительность операции (срока ссуды) через остальные параметры сделки. Рассмотрим этот вопрос подробнее.

         А) При наращивании по сложной годовой ставке i. Из исходной формулы наращения

следует, что

                                    (52)

 где логарифм можно взять по любому основанию, поскольку он имеется как в числителе, так и в знаменателе.

         Б) При наращивании по номинальной ставке процентов m раз в году из формулы

получаем

                             (53)

         В) При дисконтировании по сложной годовой учетной ставке d. Из формулы

имеем

                                    (54)

         Г) При дисконтировании по номинальной учетной ставке mраз в году. Из

приходим к формуле

                             (55)

При наращивании по постоянной силе роста. Исходя из

получаем

.                                               (56)

Расчет процентных ставок

 Из тех же исходных формул, что и выше, получим выражения для процентных ставок.

         А) При наращивании по сложной годовой ставке i. Из исходной формулы наращения

следует, что

                                               (57)

         Б) При наращивании по номинальной ставке процентов m раз в году из формулы

получаем

                             (58)

         В) При дисконтировании по сложной годовой учетной ставке d. Из формулы

Имеем                                     (59)

         Г) При дисконтировании по номинальной учетной ставке mраз в году. Из

приходим к формуле

                                      (60)

         Д) При наращивании по постоянной силе роста. Исходя из

получаем

                                       (61)

14. Определение срока платежа и ставки сложных процентов.

При разработке условий контрактов или их анализе и сравнении возникает необходимость в решении ряда, если так можно назвать, вторичных задач — определении срока ссуды и размера процентной ставки в том или ином ее виде при всех прочих заданных условиях.

Определение срока финансовой операции (m)

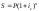
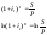
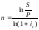
Определение ставки для сложных процентов:

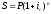
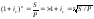
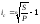
15. Начисление процентов несколько раз в году. Номинальная ставка процентов.

Номинальная ставка — это годовая процентная ставка несколько раз год (m раз)

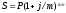— формула наращивания суммы по номинальной ставке при m-кратном начислении процентов.

Чем чаще начисляются проценты, тем быстрее идет процесс наращения (цепной процесс).

Наибольшую «прибавку» в наращении дает переход от ежегодного начисления процентов к полугодовому, наименьший эффект — переход от ежемесячного к ежедневному.

16. Сравнительный анализ графиков роста вклада по простым и сложным процентам. Сопоставление результатов наращенных сумм.

в тетради

17. Эквивалентность процентных ставок. Вывод формул эквивалентности ставок на основе равенства множителей наращения.

Процентные учетные ставки решают одни и те же задачи: определяют степень доходности операции при наращении и дисконтировании. В связи с этим возникает такой выбор ставок, при которых результаты фин.операций будут равноценны.

Ставки, обеспечивающие равноценность фин.операций, наз-ся эквивалентными.

Равноценность фин.операций может быть обеспечена в том случае, если наблюдается равенство множителей наращения или дисконтирования, т.е. 1) Rn=Rn 2)Rq=Rq

Равенство, полученное в результате соотношения множителей наращения или дисконтирования наз-ся уравнением эквивалентности

— множитель наращения

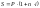— простая ставка

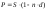— учетная ставка

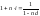— уравнение эквивалентности

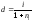
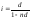
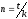
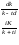
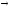
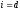
18. Уравнение эквивалентности. Вывод формул эквивалентности ставок.

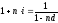— уравнение эквивалентности

Эквивалентность ставки простых процентов и ставки сложных

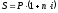— наращивание по простым

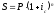— наращивание по сложным

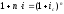
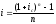
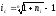
Уравнение эквивалентности простой ставки и номинальной сложной

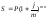
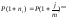
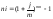
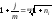
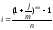
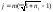
19. Принцип финансовой эквивалентности обязательств

Это принцип, на котором базируются изменения условий контрактов. Эквивалентными считаются такие платежи, которые будучи приведенными, к одному моменту времени являются равными. Приведение осуществляется путем дисконтирования или наращения. Если при изменений условий контракта принцип не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить.

Принципы изменений условий контрактов:

1. Изменение срока платежа (отдаление или приближение)

2. Объединений нескольких платежей в один (консолидация)

3. Замена одного количества платежей на другое

4. Изменение процентной ставки.

5. Сущность начисления сложных процентов. Формула сложных процентов. Формула наращения по сложной ставке. Множитель наращения и способы его определения (смешанная схема начисления процентов).

Проценты (%-ые деньги) – это доход от предоставления денег в долг, измеряются в ден. ед. Начисляются % не сразу за весь срок долга, а периодически, т.е. ежемесячно, ежеквартально, по полугодиям, ежегодно.

Сложные % — это %, начисляемые по сложной ставке.

Сложные % возрастают, т.к. каждый раз начисляются на новую сумму, которая больше предыдущей на ранее начисленные проценты:

I1=P*i

I2=(P+I1)*i

I3=(P+I1+I2)*i

Возрастают сложные проценты в геометрической прогрессии с множителем – 1+i

I1=P*i

Ik+1=Ik*(1+i)

Общая сумма % за весь срок долга находится путем суммирования % за все периоды: I=I1+I2+…+In

I=P*i+P*i(1+i)+…+P*i(1+i)^{n – 1}

т.о представляет собой сумму членов геометрич. прогрессии (bk+i=bk*q=>,

b1+b2+…+bn=b1* gⁿ – 1/g – 1),

при начислении сложных %-ов – b1=Pi

q=1+i

I=P*i*(1+i)ⁿ-1=P*i*(1+i)ⁿ-1=P[(1+I)ⁿ-1]

1+i–1 i

Формула сложных %: I= P[(1+i)ⁿ-1]

%-ая ставка – это доля дохода от исходной суммы за период начисления, измеряется в % или в долях.

Сложная ставка, если % каждый период начис-ся на различную накопленную сумму (первоанчальный долг вместе с раннее начисленными процентами), т.е. проценты начисляются на проценты, капитализация процентов.

При наращении сложных % с помощью наращения находят наращенную сумму, если известна первонач. сумма долга.

S=P+I;S=P+P[(1+I)ⁿ-1]=P(1+(1+i)ⁿ-1=P(1+i)ⁿ

Формула наращения по сложной ставке %:

S=P(1+i)ⁿ, где (1+i)ⁿ – множитель наращения по сложной ставке %, который показывает во сколько раз S>P.

Если срок долга n – дробное число, то множитель наращения рассчитывают по смешанной схеме, когда за целую часть срока начисляют сложные %, а за дробную часть – простые %.

(1+i)ⁿ=(1+i)^(1+i*), где

 — целая часть числа n

 — дробная часть числа n

(+ ) = n

6. Наращение и дисконтирование. Формулы наращения и дисконтирования по сложной ставке. Формула для расчета срока операции и размера сложной ставки.

ФМрешает 2 задачи:

1)наращение – это определение стоимости денег в будущем, если известна их стоимость на данный момент времени

2)дисконтирование – это определение стоимости денег на данный момент времени, если известна их стоимость в будущем

%-ая ставка – это доля дохода от исходной суммы за период начисления, измеряется в % или в долях.

Сложная ставка, если % каждый период начис-ся на различную накопленную сумму (первоанчальный долг вместе с раннее начисленными процентами), т.е. проценты начисляются на проценты, капитализация процентов.

С помощью наращения находят наращенную сумму долга.

S=P+I;S=P+P[(1+I)ⁿ-1]=P(1+(1+i)ⁿ-1=P(1+i)ⁿ

Формула наращения по сложной ставке %:

S=P(1+i)ⁿ, где (1+i)ⁿ – множитель наращения по сложной ставке %, который показывает во сколько раз S>P.

Из формулы наращения выводят формулу для первоначального долга, ставки и срока.

S= P(1+i)ⁿ

Формула дисконтирования по сложной ставке:

P=_S___

(1+i)ⁿ

Где 1/(1+i)ⁿ — дисконтный множитель по сложной ставке

Формула сложной ставке:

Из формулы наращения выводят формулы для ставки и срока:

1. размер ставки %: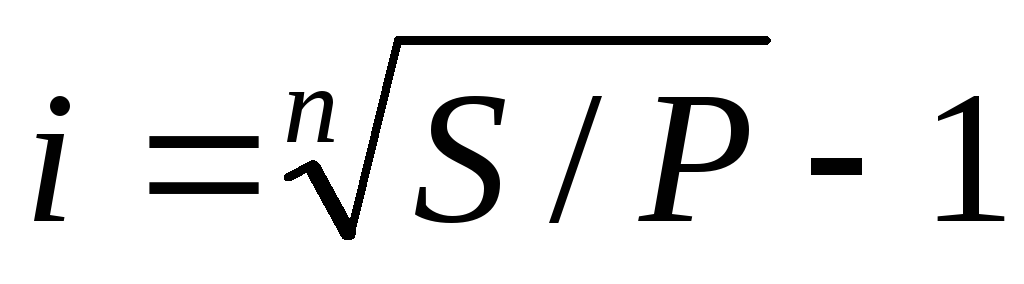

2. срок долга: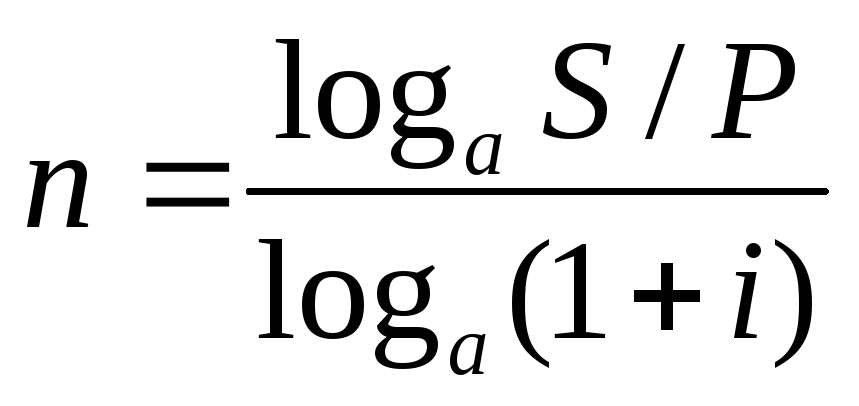

11. Наращение по сложным процентным ставкам

Сделка считается сделанными на условиях сложных процентных ставок, если доход за последующий временной период исчисляется не с первоначальной величины инвестированного капитала (Р), а с наращенной суммы предшествующих периодов. Происходит капитализация процентов, т.е. Сложные проценты применяются, в средне- и долгосрочных финансовых операциях. Приращенная сумма финансовой сделки определяется: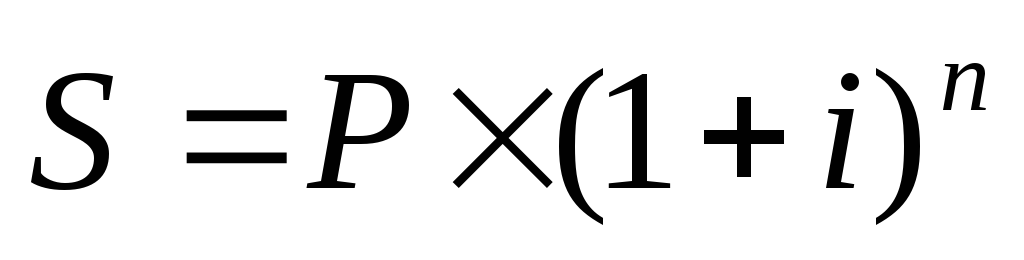

При применении в фин-ых сделках плавающихставок наращенная сумма определяется: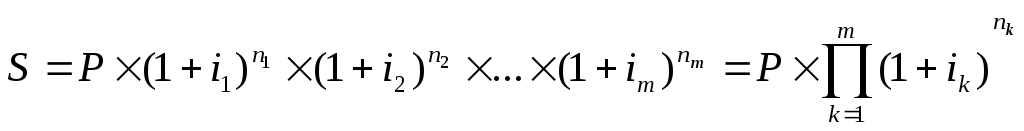

Начисление процентов производится исключительно на целую часть без учета дробной.

Однако, учесть полный срок позволяет одна из двух схем:

1. Общая схема сложных процентов: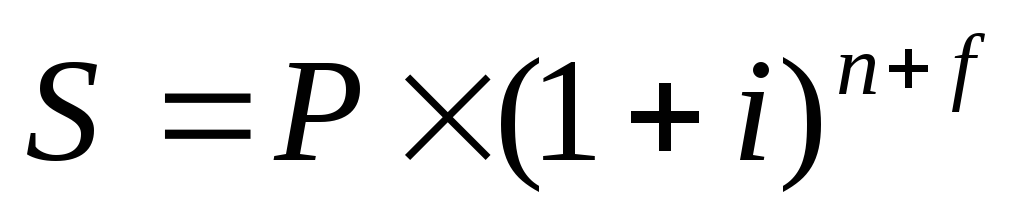

2. Смешанная схема: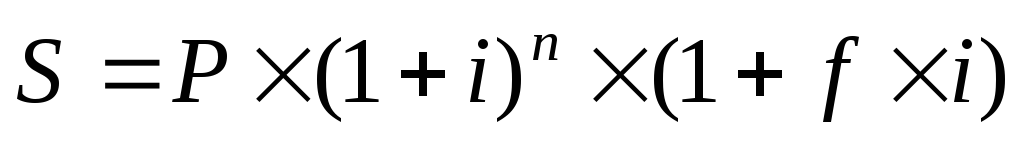

Наращенная сумма при использовании смешанной схемы будет больше чем при применении общей схемы сложных процентов.

Базовой формулой для математического дисконтирования является: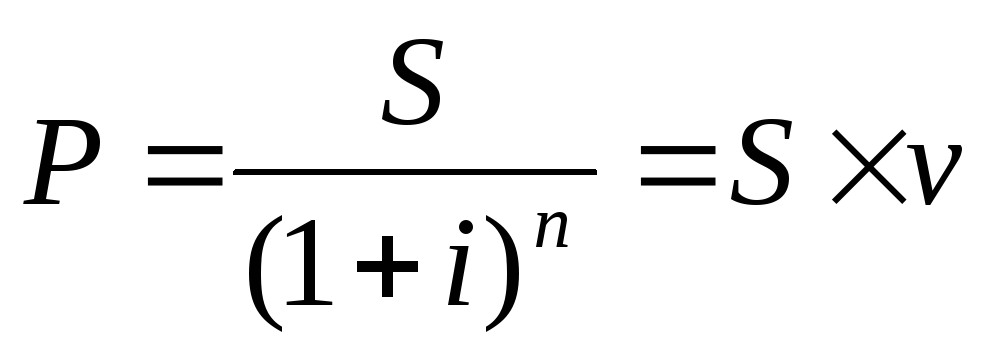Эта формула означает, что для инвестора современная величина (Р) и доход (S) планируемый к получению через n лет в будущем равнозначны с позиции своей покупательной способности.

П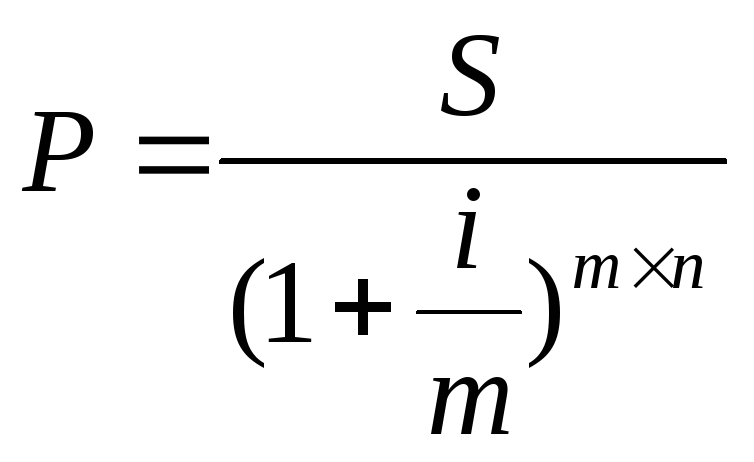ри кратном начислении процентовm раз в году формула для нахождения современной величины приобретает следующий вид:

12 Дисконтирование по сложным процентным ставкам

Оценка эффективности инвестиционных проектов основывается на их сравнении с альтернативным вариантом вложения фин. ресурсов При этом инвестору следует учитывать инфляционное обесценивание денег, периодичность начисления дохода, возможные изменения рыночной конъюнктуры.

Базовой формулой для такого анализа является: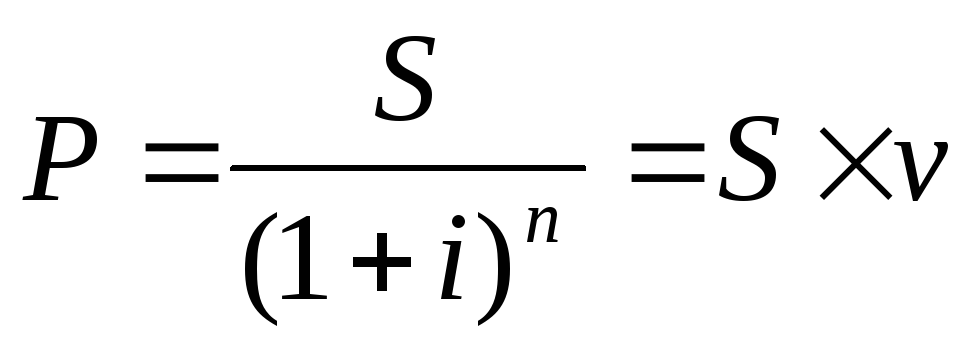

Эта формула означает, что для инвестора современная величина (Р) и доход (S) планируемый к получению через n лет в будущем равнозначны с позиции своей покупательной способности. Множитель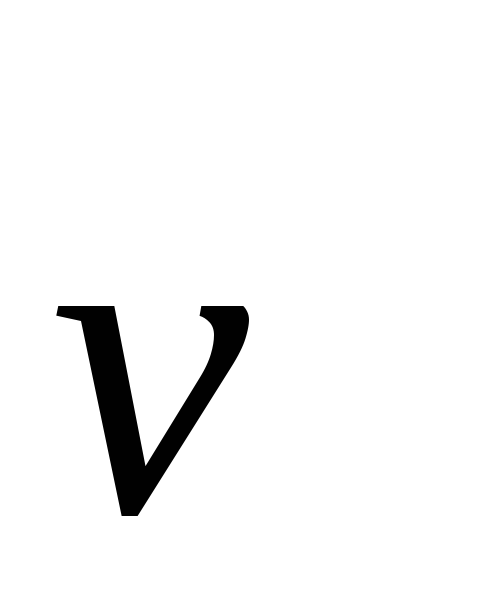называют дисконтным (учетным) множителем, который показывает «сегодняшнюю» цену одной денежной единицы будущих периодов при заданной процентной ставке. Его значение уменьшается при росте сроков реализации финансовой операции и процентной ставки по ней.

При кратном начислении процентов m раз в году формула для нахождения современной величины приобретает следующий вид: 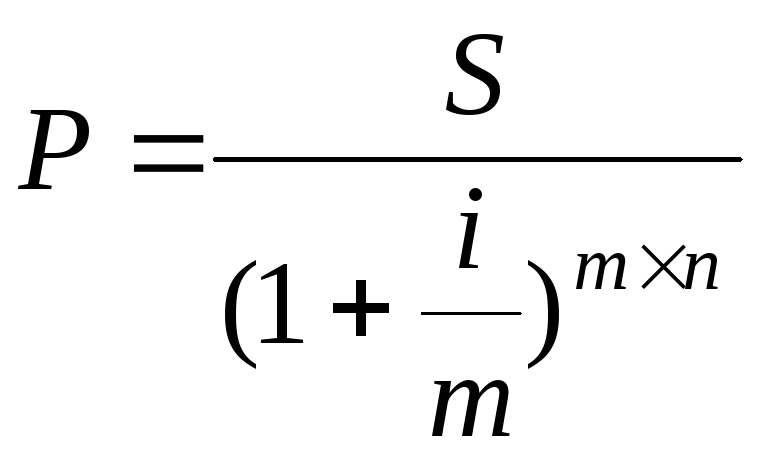При определении процентной ставки в дисконтном множителе за основу берут безрисковую ставку процентов, которая, как правило, обеспечена государством с добавлением дополнительной премии за риск, связанный с рассматриваемым проектом.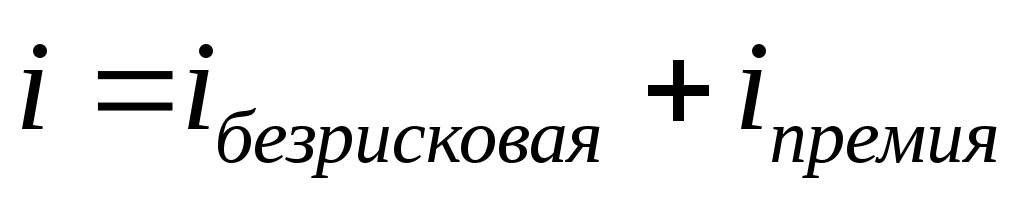Дисконтирование возможно и при дробном количестве периодов начисления процентов, применяемом в смешанных схемах, по формуле: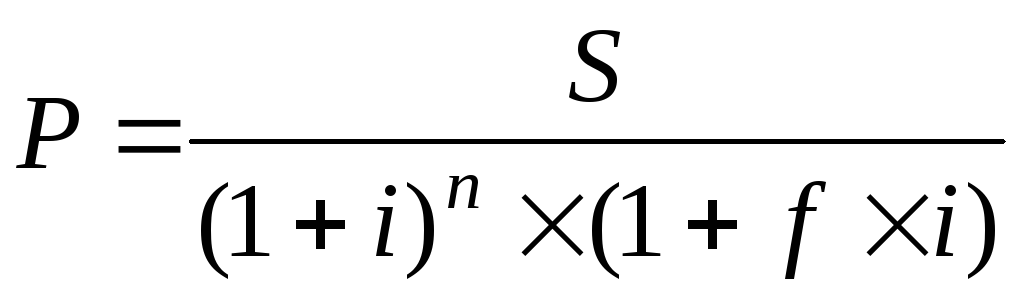

13.Операции со сложной учетной ставкой

В практике учетная ставка применяется, как правило, в случаях, когда продается долговое обяз-во ранее установленного срока погашения с дисконтом. Однако диск-ние по учетным ставкам происходит с замедлением, т. к. каждый раз учетная ставка применяется не к 1-ой сумме (как при простой ставке), а к сумме, диск-ой на предыдущем шаге времени.дисконтирование по сложной учетной ставке по форм:

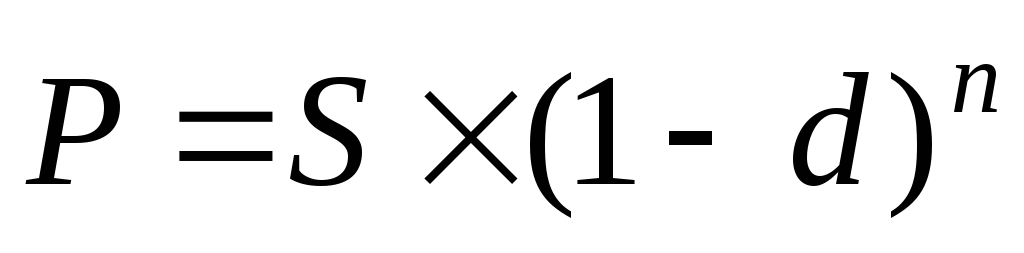, где d — сложная годовая учетная ставка.

Если срок, за который осуществляется дисконтирование, не является целым числом, то возможны следующие методы определения стоимости учтенного капитала:а) общая схема сложной учетной ставки:

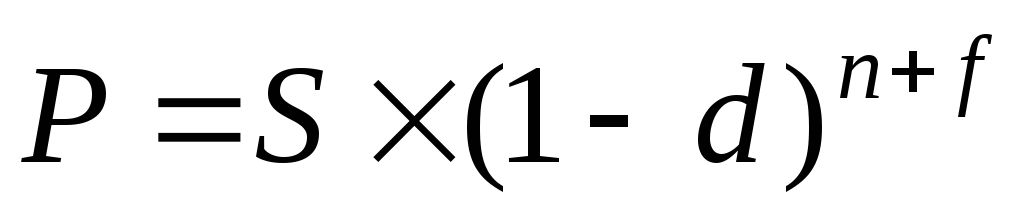б) смешанная схема:

С позиции лиц осуществляющих диск-ние наиболее пред-ым является применение:

а) сложной учетной ставки, если срок учета менее одного года;б) простой учетной ставки, если срок учета более одного года.

Дисконтирование может производиться mраз в году, при этом каждый раз учет производится по ставке 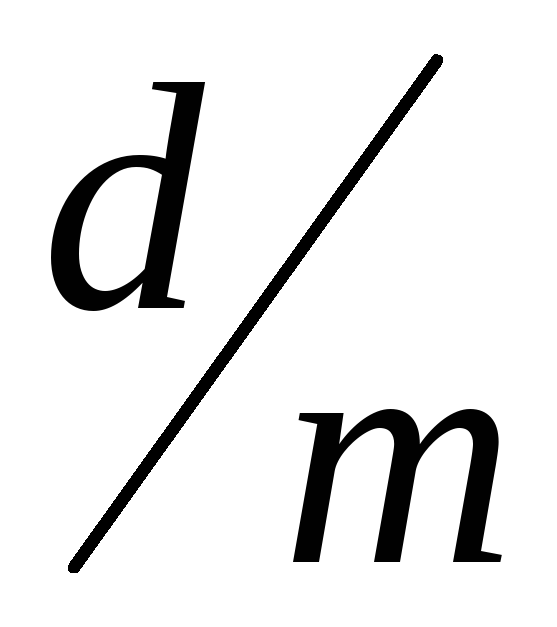, а современная величина определяется по формуле

.

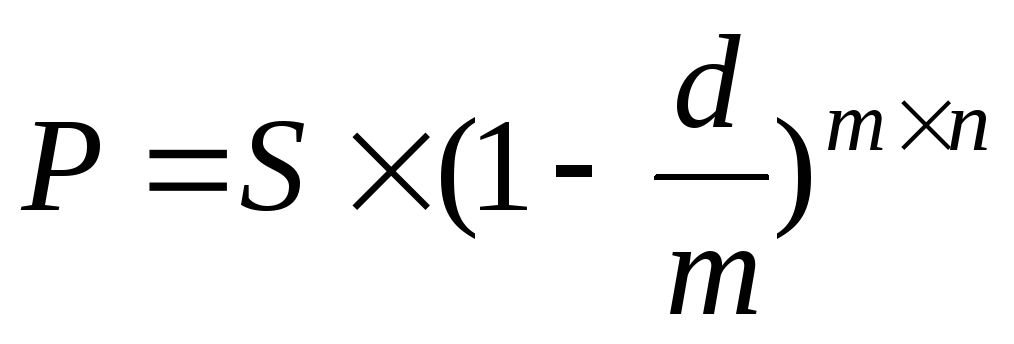2.1 Сложные проценты

Раздел II. Начисление сложных процентов

Сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют ка-

питализацией процентов.

Формула наращения по сложным процентам

Пусть первоначальная сумма долга равна P, тогда через один год сумма долга с присоединенными процентами составит P(1+i), через 2 года P(1+i)(1+i)=P(1+i)2, через n лет — P(1+i)n. Таким образом, получаем формулу наращения для сложных процентов

где S — наращенная сумма, i — годовая ставка сложных процентов, n — срок ссуды, (1+i)n — множитель наращения.

В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т.д.). Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен P, а знаменатель (1+i).

Отметим, что при сроке n<1 наращение по простым процентам дает больший результат, чем по сложным, а при n>1 — наоборот. В этом нетрудно убедиться на конкретных числовых примерах. Наибольшее превышение суммы, наращенной по простым процентам, над суммой, наращенной по сложным процентам, (при одинаковых процентных ставках) достигается в средней части периода.

Формула наращения по сложным процентам, когда ставка меняется во времени

В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид

где i1, i2,…, ik — последовательные значения ставок процентов, действующих в периоды n1, n2,…, nk соответственно.

Пример 6.

В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% в третий год, 5% в четвертый год. Определить величину множителя наращения за 4 года.

Решение.

(1+0,3)2(1+0,28)(1+0,25)=2,704

Раздел II. Начисление сложных процентов

2.1 Сложные проценты

2.2 Непрерывные проценты

 2.1 Сложные проценты

         Сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов.

Формула наращения по сложным процентам

         Пусть первоначальная сумма долга равна P, тогда через один год сумма долга с присоединенными процентами составит P(1+i), через 2 года P(1+i)(1+i)=P(1+i)², через n лет — P(1+i)ⁿ. Таким образом, получаем формулу наращения для сложных процентов

         S=P(1+i)ⁿ,                                                          (19)

где S— наращенная сумма,i  — годовая ставка сложных процентов, n — срок ссуды, (1+i)ⁿ — множитель наращения.

         В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т.д.). Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен P, а знаменатель (1+i).

         Отметим, что при сроке n<1 наращение по простым процентам дает больший результат, чем по сложным, а при n>1 — наоборот. В этом нетрудно убедиться на конкретных числовых примерах. Наибольшее превышение суммы, наращенной по простым процентам, над суммой, наращенной по сложным процентам, (при одинаковых процентных ставках) достигается в средней части периода.

Формула наращения по сложным процентам, когда ставка меняется во времени

В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид

(20)

где    i₁, i₂,…, i_k — последовательные значения ставок процентов, действующих в периоды n1, n2,…, nk соответственно.

         Пример 6.

В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% в третий год, 5% в четвертый год. Определить величину множителя наращения за 4 года.

Решение.

         (1+0,3)²(1+0,28)(1+0,25)=2,704

Формула удвоения суммы

         В целях оценки своих перспектив кредитор или должник  может задаться вопросом: через сколько лет сумма ссуды возрастет вN раз при данной процентной ставке. Обычно это требуется при прогнозировании своих инвестиционных возможностей в будущем.  Ответ получим, приравняв множитель наращения величинеN:

         а) для простых процентов

(1+ni_прост.) = N, откуда

.                                                            (21)

         б) для сложных процентов

(1+i_сложн.)ⁿ=N, откуда

.                                                    (22)

Особенно часто используется N=2. Тогда формулы (21) и (22) называются формулами удвоения и принимают следующий вид:

         а) для простых процентов

,                                                            (23)

         б) для сложных процентов

.                                                    (24)

Если формулу (23) легко применять для прикидочных расчетов, то формула (24) требует применения калькулятора. Однако при небольших ставках процентов (скажем, менее 10%) вместо нее можно использовать более простую приближенную. Ее легко получить, если учесть, что ln 2  0,7, а ln(1+i) i.  Тогда

n 0,7/i.                                                              (25)

         Пример 7.

Рассчитать, за сколько лет долг увеличится вдвое при ставке простых и сложных процентов равной 10%. Для ставки сложных процентов расчеты выполнить по точной и приближенной формуле. Результаты сравнить.

         Решение.

а) При простых процентах:

         лет.

б) При сложных процентах и точной формуле:

         года.

в) При сложных процентах и приближенной формуле:

         n 0,7/i = 0,7/0,1 =7 лет.

Выводы:

1) Одинаковое значение ставок простых и сложных процентов приводит к совершенно различным результатам.

2) При малых значениях ставки сложных процентов точная и приближенная формулы дают практически одинаковые результаты.

1. Наращение по простой процентной ставке

Простые ставки ссудных (декурсивных) процентов применя­ются обычно в краткосрочных финансовых операциях, когда ин­тервал начисления совпадает с периодом начисления (и составля­ет, как правило, срок менее одного года), или когда после каждо­го интервала начисления кредитору выплачиваются проценты. Естественно, простые ставки ссудных процентов могут приме­няться и в любых других случаях по договоренности участвующих в операции сторон.

Под наращенной суммой ссуды (долга,депозита,других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока начисления. Наращенная сумма определяется умножением первоначальной суммы долга на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной. Расчетная формула зависит от вида применяемой процентной ставки и условий наращения.

К наращению по простым процентам обычно прибегают при выдаче краткосрочных ссуд или в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются. Для записи формулы наращения простых процентов примем обозначения:

I-проценты за весь срок ссуды; 

P-первоначальная сумма долга; 

S-наращенная сумма, т.е. сумма в конце срока; 

i-ставка наращения процентов; 

n-срок ссуды.

Если срок измеряется в годах, то i означает годовую процентную ставку. Соответственно каждый год приносит проценты в сумме Pi. Начисленные за весь срок проценты составят

I=Pni.

Наращенная сумма, таким образом, находится как

S=P+I=P+Pni=P(1+ni).                    

Это выражение называют формулой простых процентов, а множитель (1+ni)-множителем наращения простых процентов. Определение современной величины Рнаращенной суммы Sназывается дисконтированием, а определение величины наращен­ной суммы S — компаундингом.

2. Дисконтирование и учет по простым процентным ставкам

При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получае­мой попрошествии интервала начисления (т. е. из наращенной суммы). Эта сумма и считается величиной получаемого кредита (или ссуды). Так как в данном случае проценты начисляются в начале каждого интервала начисления, заемщик, естественно, получает эту сумму за вычетом процентных денег. Такая опера­ция называется дисконтированием по учетной ставке, а также ком­мерческим или банковским учетом.

Дисконт— это доход, полученный по учетной ставке, т. е. раз­ница между размером кредита и непосредственно выдаваемой суммой.

Пусть теперь

d(%) — простая годовая учетная ставка;

d — относительная величина учетной ставки;

D_г — сумма процентных денег, выплачиваемая за год;

D — общая сумма процентных денег;

S— сумма, которая должна быть возвращена;

Р — сумма, получаемая заемщиком.

Тогда, согласно определениям, имеем следующие формулы:

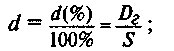
D_e=dS;

D=nD_e=ndS;

Р= S- D= S(l-nd) = S[l-(d/K)d].

Преобразуя последнее выражение, получаем формулу для оп­ределения наращенной суммы:

S=P/(1-nd)=P/(1-d*d/K)

Из этой формулы легко видеть, что в отличие от случая про­стых ставок ссудного процента простые учетные ставки не могут принимать любые значения. Именно для того, чтобы выражение имело смысл, необходимо, чтобы знаменатель дроби в пра­вой части был строго больше нуля, т. е. (1 — nd) >0, или d< 1/n. Правда, со значениями d, близкими к предельным, вряд ли мож­но встретиться в жизни.

На практике учетные ставки применяются главным образом при учете (т. е. покупке) векселей и других денежных обязательств. Из приведенных формул можно вывести еще две формулы для определения периода начисления и учетной ставки при прочих заданных условиях:

n=(S-P)/Sd

d=(S-P)/Sn=(S-P)*K/Sd

Математическим дисконтированием называется операция, когда по наращенной сумме S, периоду начисления пи про­стой процентной ставке iнужно определить первоначальную сумму Р: S = Р(1 + ni) =* Р= S/(1 + ni)

Список использованной литературы: основная литература 1-4

1. Начисление сложных годовых процентов

Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.

Формула сложного процента — это формула, по которой рассчитывается итоговая сумма с учётом капитализации (начислении процентов).

Пусть Р — первоначальная сумма,

S — наращенная сумма,

i— годовая процентная ставка (проценты сложные).

Так как проценты сложные, то в конце каждого интервала начисления процентная ставка применяется к наращенной сумме на начало этого интервала начисления.

Предположим, что первоначальная сумма Р была помещена в банк под iпроцентов годовых (проценты сложные).

Прошел 1 год. Тогда наращенная сумма S = Р(сумма на начало этого интервала начисления) + iP(проценты) = = Р(1 + i).

Прошел еще 1 год (то есть вклад лежит уже 2 года). Тогда наращенная сумма после двух лет S= Р(1 + i) (наращен­ная сумма после одного года) + iP(l + i) (проценты) = = Р(1 + i)(l + 0 = Р(1 + i)²

Прошел еще 1 год (то есть вклад лежит уже 3 года). Тогда наращенная сумма после трех лет S = Р(1 + i)²(наращенная сумма после двух лет) + iP (1 + i) (проценты) = = Р(1 + i)²(l +i) = Р(1 + i)³.

И т. д.

Если п— период начисления процентов (в годах), то на­ращенная сумма через п лет

S= Р(1 + i) ⁿ.

2. Дисконтирование по сложной ставке процента

Рассмотрим теперь антисипативный способ начисления сложных процентов.

Математическим дисконтированием называется операция, когда по наращенной сумме S, периоду начисления пи слож­ной процентной ставке iнужно определить первоначальную сумму Р.

3. Эквивалентность процентных ставок

Две ставки называются эквивалентными,если при одинаковой первоначальной сумме Ри на одинаковом периоде начисления п они приводят к одинаковой наращенной сум­ме S.

Эквивалентные процентные ставки— это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.

При сравнении двух ставок из разных классов для одной из них находят эквивалентную ей ставку из другого класса и проводят сравнение двух ставок из одного класса.

Эквивалентные процентные ставки необходимо знать в случа­ях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения раз­личных процентных ставок.

Для нахождения эквивалентных процентных ставок использу­ют уравнения эквивалентности, принцип составления которых за­ключается в следующем. Выбирается величина, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух вы­ражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между про­центными ставками различного вида.

Повторим формулы для определения наращенной суммы при различных способах начисления процентов, полученные в пре­дыдущих вопросах этой темы:

Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различ­ными процентными ставками.

Список использованной литературы: основная литература 1-4

1. Понятие ренты, ее виды

Потоки платежей весьма часто встречаются на практике. Заработная плата выплачивается, как правило, в виде потока платежей 2 раза в месяц, примерно через 15 дней. Плата за квартиру — поток, как правило, ежемесячных платежей. Семья откладывает на покупку автомобиля, внося ежемесячно на счет в банк некоторую сумму, и т.д. Регулярные взносы в пенсионный фонд — это пример аннуитета. Поэтому изучение потоков платежей очень важно.

Поток платежей — это последовательность величин самих платежей (со знаками) и моментов времени, когда они осуществлены.

Платеж со знаком плюс, который может быть опущен, — это поступление, платежи со знаком минус представляют собой выплаты.

Рентой называется последовательность периодических выплат, обычно равных по величине, осуществляемых через равные промежутки времени.

Аннуитет (финансовая рента)— это ряд последователь­ных платежей через одинаковые промежутки времени.

Наиболее распространенными примерами рент являются выплаты по облигациям, премии по страхованию, выплаты потребительских кредита и т.д.

Привести пример аннуитета.

Rj— это величина отдельного платежа ренты.

Временной интервал между двумя последовательными выплатами называется периодом ренты.

Срок от начала первого периода до конца последнего называется сроком ренты.

Интервал ренты— это время между двумя последовательными платежами. Если все платежи равны между собой, то это постоянная рента, иначе — переменная рента.

Различают два основных типа рент:

1. Безусловные ренты — это ренты с фиксированным сроком, т.е. даты первой и последней выплаты определены до начала ренты.

2. Условные ренты — ренты, в которых дата первой или последней выплаты зависит от некоторого события. Например, пенсия или премия по страхованию жизни.

Виды ренты:

1. обычная илипостнумерандо, выплаты производятся в конце каждого периода

2. приведенная (авансированная или пренумерандо), если выплаты — в начале каждого периода.

Поток называется конечным или бесконечным в зависимости от количества платежей в нем.

Для расчета наращения или дисконтирования платежей используется сложная процентная ставка i.

Наращенная (будущая) сумма ренты S— это все платежи вместе с процентами на дату последней выплаты.

Современная (приведенная) стоимость ренты — это все платежи вместе с процентами, пересчитанные на начальный момент времени ренты с помощью операции математического дисконтирования.

Существуют ренты:

1. верные(выплата не ограничена никакими условиями)

2. условные (выплата обусловлена наступ­лением какого-то события). Страховые взносы — это пример условной ренты.

Срок реализации отложенных рент откладывается на некоторое время.

Пусть р— число рентных платежей в году, а число mпоказывает, сколько раз в году начисляются проценты.

Ренты, для которых р= m, называются простыми.

Ренты, для которых р ≠ m, называются общими.

2. Понятие простой ренты и расчеты, связанные с нахождением ее параметров

Текущим значением ренты называется денежная сумма, эквивалентная множеству всех выплат в начальный момент ренты.

Наращенным значением (суммой) ренты называется сумма, эквивалентная множеству всех выплат в конце всего срока ренты.

Для обычной ренты текущее значение определяется за один период до первой выплаты, а наращенное значение — в момент последней выплаты. Очевидно, что и текущее, и наращенное значение зависят от процентной ставки, используемой в уравнении эквивалентности. Так период ренты может совпадать или не совпадать с периодом начисления процентов. Ренты по этому признаку классифицируются на простые и общие соответственно.

Пусть R— ежегодные платежи, на которые начисляются проценты в конце каждого года по сложной процентной став­ке i, n— срок ренты.

R R R …R R R

0 1 2 3 … n-2 n-1 n

Платеж в конце 1-го года даст наращенную сумму R(l + i)^n-1. Платеж в конце 2-го года даст наращенную сум­му R (1 + i)^n-1. Платеж в конце 3-го года даст наращенную сумму R (1 + i)^n-3 и т. д.

Наращенная (будущая) сумма ренты S = R(l + i)^n-1 + R(l + i)^n-2+ R(l + i)^n-3+ + … + R(l + i)ⁿ + R. Мы получили сумму nпервых членов геометрической прогрессии с b = Rи знаменателем q= 1 + i.

S=b₁(gⁿ-1)/ (g-1) = R((1-i)ⁿ -1) / ((1-i) -1) = R((1-i)ⁿ -1) / i

R R R …R R R

01 2 3 …n-2 n-1 n

Платеж в конце 1-го года даст современную стоимость R(l + i)ⁿ. Платеж в конце 2-го года даст наращенную сумму R(l + i)^n-1. Платеж в конце 3-го года даст наращенную сум­му R(l + i)^n-2И т. д.

Наращенная (будущая) сумма ренты S = R(l + i)ⁿ + R(l + i)^n-1+ R(l + i)^n-2+ + … + R(l + i)²R(l + i). Мы получили сумму nпервых членов геометрической прогрессии с b = Rи знаменателем q= 1 + i.

S=b₁(gⁿ-1)/ (g-1) = R*(1-i)* ((1-i)ⁿ -1) / ((1-i) -1) = R*(1-i)* ((1-i)ⁿ -1) / i

R R R …R R R

01 2 3 …n-2 n-1 n

Платеж в конце 1-го года даст современную стоимость R/(l + i). Платеж в конце 2-го года даст наращенную сумму R/(l + i)². Платеж в конце 3-го года даст наращенную сум­му R/(l + i)³И т. д.

Современная стоимость рентыА = R/(l+ i) + R/(l + i)² + R/(l + i)³ +…+ R/(l + i)^n-1 + R/(l + i)ⁿ.Мы получили сумму nпервых членов геометрической прогрессии b1=R/(l+ i) и знаменателем q = 1/(1 + i).

ТогдаА= b₁(gⁿ-1)/ (g-1) =R/(l + i)*(1/(1+i)ⁿ-1)/ (1/(1+i)-1)=

=R(1-1/(1+i)ⁿ)/i

Это современная стоимость простой ренты постнумерандо. Подставив в эту формулу вместо Rвеличину R(l + i), мы получим современную стоимость простой ренты пренумерандо

А= R*(1+i)*(1-1/(1+i)ⁿ)/i

Зная процентную ставку i, количество выплат n и наращенную сумму S(или современную стоимость А) простой ренты, можно определить величину отдельного платежа R. Для простой ренты постнумерандо наращенная (будущая) сумма ренты S=R((1-i)ⁿ -1) / I. Отсюда R=S*i/ ((1-i)ⁿ -1)

Для простой ренты пренумерандо наращенная (будущая)сумма ренты S=R*(1-i)* ((1-i)ⁿ -1) / I

Отсюда R=S*i/ (1+i)*((1-i)ⁿ -1))

Зная величину отдельного платежа R, процентную ставку iи наращенную сумму S (или современную стоимость А) простой ренты, можно определить количество выплат n.

Для простой ренты постнумерандонаращенная (будущая) S=R((1-i)ⁿ -1) / I.

Отсюда (1 + i)ⁿ — 1 = Si/R =>

n= ln (1+ Si/R) /ln (1+i)

Подставив в последнюю формулу вместо Rвыражение R(1-i).мы получим срок ренты пренумерандо:

n= ln (1+ Si/R(1+i)) /ln (1+i)

А= R*(1-1/(1+i)ⁿ)/I

Отсюдаn =-ln (1-Ai/R) /ln (1+i)

Подставив в последнюю формулу вместо Rвыражение R(1+i), мы получим срок ренты пренумерандо:

n =-ln (1-Ai/R(1+i)) /ln (1+i)

Зная величину отдельного платежа R, количество выплат nи наращенную сумму S (или современную стоимость А) простой ренты, можно попытаться найти процентную ставку. Но получается нелинейное уравнение.

Срок реализации отложенных рент откладывается на некоторое время — период отсрочки.

Список использованной литературы: основная литература 1-4

3. Понятие общей ренты и расчеты, связанные с нахождением ее параметров

Подставив в формулу для наращенной суммы простой ренты S=R((1-i)ⁿ -1) / I. и выражения R = Wi/((1 + i)^m/P— 1).мы найдем наращенную сумму общей ренты:

S = W((1-i)ⁿ -1) / ((1 + i)^m/P— 1).

Здесь n— это общее количество интервалов начисления процентов за весь срок ренты.

Подставив в формулу для современной стоимости простой рентыА=R*(1-1/(1+i)ⁿ)/I выражение R = Wi/((1 + i)^m/P— 1), мы найдем современную стоимость общей ренты: А = W*I*(1-1/(1+i)ⁿ)/ ((1 + i)^m/P— 1)

4. Преобразование простой ренты в общую ренту.

Пусть р— число рентных платежей в году, а число mпоказывает, сколько раз в году начисляются проценты. Для об­щей ренты р ≠m, а для простой ренты р = m.

Для простой ренты довольно несложно определяются все ее параметры. Поэтому для вычисления параметров общей ренты очень важно уметь преобразовывать общую ренту в простую ренту.

Пусть Wи R— величины выплат общей и простой рент соответственно, р — число рентных платежей в году для общей ренты, m— число интервалов начисления процентов в году, jи i — процентные ставки за интервал начисления про­центов общей и простой рент соответственно, n— общее чис­ло интервалов начисления процентов.

Данные ренты эквивалентны, то есть процентные ставки за периоды рент совпадают и эквивалентные этим рентам зна­чения, соответствующие одному и тому же моменту времени, совпадают. Тогда (1 + j)^p = (1 + i)^m =>j= (1 + i)^m/P— 1.

Наращенные суммы для обеих рент одинаковы:

R*(1-i)* ((1-i)ⁿ -1) / I — 1)= W((1 + i)^m/P— 1)/j

R/I = W/j R= Wi/j = Wi/((1 + i)^m/P— 1)

5. Простая бессрочная рента. Общая бессрочная рента. Бессрочная рента пренумерандо.

Под «вечной» годовой рентой понимается рента, последовательность платежей которой неограниченна, предполагается, что рента будет выплачиваться неограниченно долго.

Бессрочная рента — это рента, выплаты которой не ограничены никаким сроком. Существует множество примеров бессрочных рент, простейший из них, наверно, — последовательность периодических выплат процентов на продуктивно инвестированный капитал. Классификация бессрочных рент (на обычные, приведенные, отложенные и т.д.) полностью совпадает с классификацией рент (конечных), которые рассматривались выше. Например, обычная простая бессрочная рента — это множество периодических платежей, производимых бесконечно долго в конце каждого последовательного периода начисления процентов. Простая бессрочная рента

Бессрочная рента не ограничена никаким сроком, то есть срок ренты

n→∞.

R R R … R R R

01 2 3 …n-2 n-1 n

Современная стоимость простой бессрочной ренты

A=R/i. ОтсюдаR = Ai.

Общая бессрочная рента — это бессрочная рента, для которой период выплат отличается от периода начисления процентов.

Бессрочная рента пренумерандо отличается от бессрочной ренты постнумерандо только платежом в момент времени t= 0. Поэтому для простой бессрочной ренты пренумерандо современная стоимостьА — R + R/i, а для общей бессрочной ренты пренумерандо современная стоимость

А= W + R/i = W+ Wi/((1 + i)^m/P— 1)i= W/(1-1/(1 + i)^m/P)

Список использованной литературы: основная литература 1-4