Калькулятор расчета аннуитетного платежа по кредиту: Кредитный калькулятор онлайн

Июл 09 2018

Содержание

Калькулятор онлайн — Кредитный калькулятор

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или $ \frac{1}{100} $ часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р.

(сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100.

Например:

$ 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 $

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

$ 0,58 = (0,58 \cdot 100)\% = 58\% $ $ 0,045 = (0,045 \cdot 100)\% = 4,5\% $

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,

— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.

Чтобы найти $ \frac{p}{100} $ от a, надо a умножить на $ \frac{p}{100} $:

$ b = a \cdot \frac{p}{100} $

Итак, чтобы найти р% от числа, надо это число умножить на дробь $ \frac{p}{100} $. Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью $ \frac{p}{100} , \; (p \neq 0) $, надо b разделить на $ \frac{p}{100} $:
$ a = b : \frac{p}{100} $

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на $ \frac{p}{100} $. Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а $ (a \neq 0) $, надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

$ p = \frac{b}{a} \cdot 100\% $ Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют $ \frac{9 \cdot 100}{180} = 5\% $ раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

$ b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) $ взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p.

Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или $ \frac{pn}{100}S $, а всего придется заплатить $ S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S $

Таким образом:
$ S_n = \left( 1+ \frac{pn}{100} \right) S $

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
$ S_n = \left( 1- \frac{pn}{100} \right) S $

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает.

Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет $ \frac{p}{100}S $ р., и через год на счете окажется сумма
$ S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S $
то есть начальная сумма увеличится в $ 1+ \frac{p}{100} $ раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
$ S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S $

Аналогично $ S_3 = \left( 1+ \frac{p}{100} \right)^3 S $ и т. n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

расчет потребительского кредита, ежемесячных платежей и выплат по процентам займа – банк Промсвязьбанк

Получите и погашайте кредит там, где удобно вам!

Теперь вы сможете получить потребительский кредит наличными или внести ежемесячный платеж в любом офисе Промсвязьбанка – рядом с домом или по пути на работу. При этом совершенно не важно, в каком офисе вы подавали заявку на кредит.

Рассчитайте сумму ежемесячных платежей по потребительскому кредиту в зависимости от вашего дохода или от суммы кредитования.

Получите и погашайте кредит там, где удобно вам! Теперь вы сможете получить потребительский кредит наличными или внести ежемесячный платеж в любом офисе Промсвязьбанка – рядом с домом или по пути на работу. При этом совершенно не важно, в каком офисе вы подавали заявку на кредит.

Давно мечтаете о путешествии или туристической поездке, но никак не получается накопить?
Квартира требует ремонта, но нет достаточной суммы на счету?
Хотите купить мебель или бытовую технику в рассрочку?
Не откладывайте жизнь на завтра! Потребительские кредиты от Промсвязьбанка помогут вам реализовать свои мечты, позаботиться о будущем уже сейчас. Выгодные условия, отсутствие скрытых комиссий, удобное погашение – из года в год мы стараемся сделать наши услуги кредитования максимально комфортными и прозрачными для вас.
Потребительский кредит наличными — один из самых популярных видов краткосрочного кредитования населения. Вы можете получить денежный займ на любые цели:

дорогостоящие крупные покупки;
обучение;
медицинское обслуживание;
отдых и туристические поездки;
ремонт, строительные работы и пр.

Преимущества кредитных программ в Промсвязьбанке:

ежегодное снижение ставки по кредиту в случае безупречного погашения.
кредиты наличными по льготной (сниженной) процентной ставке для постоянных клиентов.
выгодные условия кредитования для вкладчиков банка.
возможность оформить кредит за 30 минут, представив всего лишь 2 документа.
возможность «уйти на кредитные каникулы» и отсрочить 2 платежа.

Кроме того, для держателей наших зарплатных карт и сотрудников аккредитованных компаний разработана упрощенная процедура получения кредита и льготные условия.
Получить подробную консультацию по продуктам у сотрудников банка можно по телефону 8-800-555-20-20 (звонок по России бесплатный) или Позвонив онлайн с сайта.

🖩 Кредитный калькулятор, рассчитать потребительский кредит на калькуляторе онлайн для физических лиц от банка Восточный

Расчет кредита на онлайн калькуляторе

Все продукты банка «Восточный» отличаются доступностью, понятными гибкими условиями и упрощенной процедурой выдачи. В момент подписания договора заемщикам становятся точно известными размер переплаты и ежемесячного платежа. Эти данные также можно узнать предварительно с помощью кредитного калькулятора, до подачи заявки, чтобы объективно оценить личные финансовые возможности.

На нашем официальном сайте размещен калькулятор с возможностью рассчитать платежи онлайн, использовать который можно всегда, в любое удобное время.

Расчет процентов по кредиту

Динамичный, наглядный, бесплатный калькулятор для расчета ежемесячного платежа, суммы переплаты и процентной ставки, который позволяет сделать следующее:

выбрать сумму займа в рамках лимита;
указать приемлемый срок кредитования;
узнать сумму ежемесячного платежа и переплаты.

Параметры для расчета можно менять, вводить многократно, результаты появляются мгновенно, без обновления страницы. Полученные значения носят ознакомительный характер. Их целесообразно сравнить со своим доходом. Статистика свидетельствует, что безболезненная для бюджета сумма ежемесячного платежа должна составлять не более 30 % от доходов заемщика или его семьи. Рекомендуем учесть эти данные при расчетах.

Для использования сервиса нажмите на пункт «Рассчитать», введите исходные данные, проанализируйте результат. Простой, понятный интерфейс не вызывает затруднений даже у неопытных пользователей.

Калькулятор рассчитывает займы для физических лиц по стандартным формулам и алгоритмам. Заемщикам не нужно изучать способы начисления процентов, производить сложные математические действия. Просто используйте готовые данные для оценки платежеспособности по условиям банка.

Погашение долга

Даже тщательно спрогнозированные планы подвержены влиянию жизненных обстоятельств. Каждый заемщик может оказаться в сложной финансовой ситуации. Если по каким-либо причинам вы не можете сделать очередной платеж, следует обсудить проблему с менеджером банка, выяснить возможность отсрочки возврата долга за счет увеличения срока платежей.

В случае объективных затруднений с выплатами мы готовы в индивидуальном порядке предоставить кредитные каникулы сроком на 1–3 месяца. В течение этого времени заемщик вносит только проценты по кредиту. Срок договора продлевается на период отсрочки платежей.

К договору прилагается график платежей ссуды. В нем указаны даты внесения и размер ежемесячного платежа. Эту же информацию можно узнать по телефону, а также с помощью дистанционных сервисов.

По всем кредитным продуктам у нас разработаны несколько бесплатных вариантов погашения:

наличными в кассе банка;
через терминалы с функцией приема наличных;
переводом с помощью системы «Интернет-банк» и мобильного приложения.

Несколько источников информации и способов погашения позволяют легко соблюдать финансовую дисциплину.

Формула расчета ипотеки

Два вида ипотечных платежей

Ипотечные платежи бывают аннуитетными и дифференцированными. При аннуитетных платежах размер ежемесячного платежа неизменен на протяжении всей ипотеки. Размер ежемесячных платежей при дифференцированной схеме постоянно уменьшается. Аннуитетные платежи более распространены, чем дифференцированные. Читайте подробнее про аннуитетные и дифференцированные платежи.

Расчет ипотеки для аннуитетных платежей

Ежемесячная процентная ставка

Для начала нам понадобится рассчитать ежемесячную процентную ставку по кредиту:

ЕЖЕМЕСЯЧНАЯ_СТАВКА = ПРОЦЕНТНАЯ_СТАВКА_ГОДОВЫХ / 12 / 100

Для процентной ставки 9.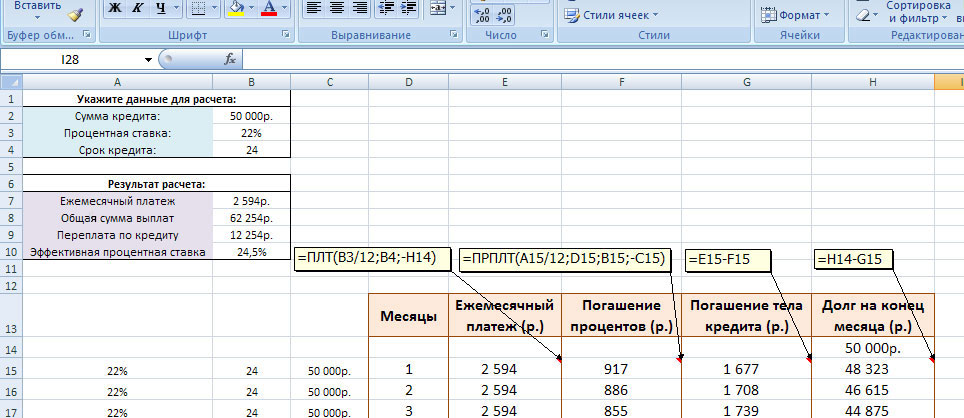 (20 лет * 12 (месяцев / год)) = 6.77 ЕЖЕМЕСЯЧНЫЙ_ПЛАТЕЖ = 1 500 000 руб * 0.008 * 6.77 / (6.77 — 1) = 14 080 руб

Основной долг и проценты

Мы вычислили размер ежемесячного платежа по ипотеке при аннуитетной схеме платежей. Рассчитаем какая часть платежа идет на погашение основного долга, а какая на погашение процентов:

ПРОЦЕНТНАЯ_ЧАСТЬ = ОСТАТОК_ДОЛГА * ЕЖЕМЕСЯЧНАЯ_СТАВКА
ОСНОВНАЯ_ЧАСТЬ = ЕЖЕМЕСЯЧНЫЙ_ПЛАТЕЖ - ПРОЦЕНТНАЯ_ЧАСТЬ

Эти величины меняются с каждым платежем, так как меняется остаток долга. Рассмотрим первый платеж для ипотеки из примера выше:

ПРОЦЕНТНАЯ_ЧАСТЬ = 1 500 000 руб * 0.008 = 12 000 руб
ОСНОВНАЯ_ЧАСТЬ = 14 080 руб - 12 000 руб = 2 080 руб

Переплата

Размер переплаты за кредит рассчитывается так:

ПЕРЕПЛАТА = ЕЖЕМЕСЯЧНЫЙ_ПЛАТЕЖ * СРОК_ИПОТЕКИ_МЕСЯЦЕВ - СУММА_КРЕДИТА

Для ипотеки из примера выше:

ПЕРЕПЛАТА = 14 080 руб * (20 лет * 12 (месяцев / год)) - 1 500 000 руб = 1 879 200 руб

График аннуитетных платежей

На рисунках — график и таблица платежей для рассматриваемого примера. СРОК_ИПОТЕКИ_МЕСЯЦЕВ ЕЖЕМЕСЯЧНЫЙ_ПЛАТЕЖ = СУММА_КРЕДИТА * ЕЖЕМЕСЯЧНАЯ_СТАВКА * ОБЩАЯ_СТАВКА / (ОБЩАЯ_СТАВКА — 1) ОСТАТОК_ДОЛГА = СУММА_КРЕДИТА в цикле для каждого ТЕКУЩИЙ_МЕСЯЦ в ипотеке: ПРОЦЕНТНАЯ_ЧАСТЬ = ОСТАТОК_ДОЛГА * ЕЖЕМЕСЯЧНАЯ_СТАВКА ОСНОВНАЯ_ЧАСТЬ = ЕЖЕМЕСЯЧНЫЙ_ПЛАТЕЖ — ПРОЦЕНТНАЯ_ЧАСТЬ ОСТАТОК_ДОЛГА = ОСТАТОК_ДОЛГА — ОСНОВНАЯ_ЧАСТЬ добавить (ТЕКУЩИЙ_МЕСЯЦ; ПРОЦЕНТНАЯ_ЧАСТЬ; ОСНОВНАЯ_ЧАСТЬ) на график

Расчет ипотеки калькулятором

Намного проще воспользоваться готовым ипотечным калькулятором, который сам рассчитает ипотеку по вышеприведенным формулам. Это будет значительно быстрее, чем считать это самостоятельно 🙂

Мы подготовили Google Таблицу для самостоятельного расчета аннуитетного платежа. Редактирование: Файл -> Создать копию.

Расчет ипотеки для дифференцированных платежей

Ежемесячный процент

Ежемесячный платеж считается так же, как и ежемесячный процент аннуитетных платежей.

Ежемесячный платеж

При дифференцированных платежах основной долг гасится равномерно в течение всего срока кредитования. Рассчитаем долю ежемесячного платежа, идущую на погашение основного долга:

ЕЖЕМЕСЯЧНОЕ_ПОГАШЕНИЕ_ДОЛГА = СУММА_КРЕДИТА / СРОК_ИПОТЕКИ_МЕСЯЦЕВ

Если мы берем ипотечный кредит на сумму 1 500 000 руб на 20 лет, то

ЕЖЕМЕСЯЧНОЕ_ПОГАШЕНИЕ_ДОЛГА = 1 500 000 руб / (20 лет * 12 месяцев / год) = 6 250 руб

Ежемесячное погашение процентов считается так же, как и для аннуитетных платежей:

ПРОЦЕНТНАЯ_ЧАСТЬ = ОСТАТОК_ДОЛГА * ЕЖЕМЕСЯЧНАЯ_СТАВКА

Итого ежемесячный платеж это сумма процентной части и части на погашение основного долга. Эта сумма каждый месяц пересчитывается и уменьшается, так как размер основного долга уменьшается.

Для первого платежа из рассматриваемого примера это будет:

ПОГАШЕНИЕ_ДОЛГА = 1 500 000 руб / (20 лет * 12 месяцев / год) = 6 250 руб
ПРОЦЕНТНАЯ_ЧАСТЬ = 1 500 000 руб * 0.008 = 12 000 руб
ПЛАТЕЖ_ЗА_МЕСЯЦ = 6 250 руб + 12 000 руб = 18 250 руб

Обратите внимание, что в начале кредита ежемесячный платеж при дифференцированной схеме (18 250 руб) больше, чем аннуитетной схеме (14 080 руб). Но при этом чуть бОльшая (6 250 руб против 2 080 руб) часть платежа идет на погашение долга.

График дифференцированных платежей

На рисунках — график и таблица дифференцированных платежей для рассматриваемого примера. Их построил наш ипотечный калькулятор (ссылка ведет на расчет рассматриваемого примера).

Они рассчитывается аналогично аннуитетным платежам.

Кредитный калькулятор | Деньги.VL

Не смотря на то, что жизнь в целом дорожает, возможностей в ней становится все больше. Большинство людей уже давно живут «в долг» и не боятся этого: кредит берется на квартиру или дом, машину, открытие бизнеса и многое другое.

В нашей стране многие до сих пор относятся к кредитам с опаской. Не удивительно: большинство банков достаточно сложно описывают условия и правила погашения кредитов, в результате чего даже экономисту бывает не под силу самостоятельно посчитать, сколько всего денег придется отдать. Для того, чтобы помочь в этом вопросе потенциальным заемщикам, и был создан кредитный калькулятор.

Его можно найти на сайтах большинства банков, а также существуют свободные кредитные калькуляторы, не привязанные к конкретному банку.

Итак, решение о необходимости кредита принято, подходящий кредитный калькулятор – найден, осталось только рассчитать кредит. Для этого в соответствующие поля необходимо ввести общую сумму кредита, его срок и процентную ставку, а также указать нужный вид платежей.

Этот последний вопрос многих вводит в ступор. Отечественный потребитель погашение кредита обычно представляет себе как ежемесячную выплату равных сумм. В банковской терминологии это называется аннуитетный платеж. Банк рассчитывает общую сумму процентов, которые придется выплатить за весь срок кредита, прибавляет занимаемую сумму и делит получившееся число на количество месяцев. Неприятным сюрпризом здесь оказывается то, что в первые месяцы заемщик фактически выплачивает проценты, а сама сумма долга не уменьшается.

Однако есть и еще один вариант: дифференцированный платеж. В этом случае погашать придется каждый месяц равную часть тела кредита + проценты на оставшуюся сумму. В результате график выплат будет выглядеть как нисходящая кривая: с каждым месяцем придется расставаться со все меньшей суммой. Особенно удобен этот вид кредитования, если Вы надеетесь погасить часть кредита досрочно.

Проводя при помощи калькулятора предварительный расчет выплаты за кредит, имеет смысл посмотреть, как будет выглядеть погашение долга и первым, и вторым способом. Обратив внимание на то, с какой суммой придется расставаться каждый месяц и сколько нужно будет переплатить за весь срок, можно будет легко выбрать банк и вид кредита, наиболее подходящий для Ваших условий.

Кредитный калькулятор | Потребительские кредиты

ЦБ РФна 6 фев $ 75,1107 (−0,6186) € 89,8850 (−1,0356) КС 4,25% год Finam.

ru: нефть Brent 59,61$ (-0,01) Внимание!
Кредитный калькулятор может быть использован для ПРИМЕРНОГО расчета и сравнения ежемесячных платежей. Для получения более точных данных обращайтесь в кредитную организацию, в которой Вы собираетесь оформлять кредит.

Расчет производится по стандартным формулам аннуитетных и дифференцированных платежей на основании следующих факторов: сумма кредита, срок кредита, годовой процент. При расчете не учитываются: доп. комиссии. Замечания и пожелания: [email protected]

Нашли ошибку? Выделите текст и нажмите Ctrl+Enter

Как самостоятельно рассчитать кредит | «Кредитный калькулятор»

Как правило, кредитный калькулятор позволяет использовать для расчетов стандартные формулы, полученный результат легко можно проверить, воспользовавшись обычным калькулятором и нижеприведенными формулами. Кредитный калькулятор позволяет рассчитать сумму выплат, которую требуется выплачивать ежемесячно с целью погашения кредита, выгодную процентную ставку, а также дает возможность вычислить, какая сумма отчисляется на погашение основного кредита, а какая – на погашение начисляемых процентов.

Посредством кредитного калькулятора можно осуществить два вида платежей:

Дифференцированные платежи представляют собой ежемесячные выплаты по кредиту, которые к концу срока договора кредитования уменьшаются. Данные платежи состоят из определенной доли основного долга, а также процентов, которые начисляются на оставшуюся невыплаченную сумму кредита. Используются они зачастую в Сбербанке.
Аннуитетные платежи представляют собой равные по сумме ежемесячные платежи, состоящие из доли основного долга и суммы процентов, начисленных за пользование кредитом. Такие платежи довольно часто применяются в коммерческих банках.

Кроме того, кредитный калькулятор используется для сравнения разных типов займов, а также получения необходимой информации без помощи специалистов банка.

Как рассчитывается дифференцированный платеж

Дифференцированные платежи уменьшаются по мере уменьшения срока кредита, они между собой не равны. Дифференцированный платеж включает две части:

Фиксированная сумма, которая предназначена для погашения основной задолженности.
Убывающая часть, состоящая из процентов, начисляемых на оставшуюся сумму кредита.

Вследствие того, что основной долг постоянно уменьшается, снижается и размер начисляемых процентов, а также и сумма ежемесячного платежа.Для исчисления суммы основного долга требуется сумму кредита первоначального разделить на количество периодов (срок кредита):

ВД = ПСК / СК

ВД – возврат долга основного, ПСК – первоначальная кредитная сумма, СК – срок кредита.

Это основная формула, по которой можно рассчитать сумму оставшегося основного долга. Однако в каждом банке имеются свои отличительные особенности при вычислении суммы процентов. Среди основных подходов можно выделить два, их разница заключается во временном периоде.Некоторые банки рассчитывают проценты исходя из того, что год состоит из двенадцати месяцев. В таком случае ежемесячные проценты определяют по следующей формуле:

СНП = ООД х ПГС / 12

СНП – сумма начисляемых процентов, ООД – остаток основного долга, ПГС — процентная годовая ставка.

ругие же банки исходят из того, что год состоит из трехсот шестидесяти пяти дней. Подобный подход основывается на расчете точных процентов при точном числе дней ссуды. В таком случае сумма ежемесячных процентов исчисляется по следующей формуле:

СНП = ООД х ПГС х КДМ / 365

СНП – сумма начисляемых процентов, ООД – остаток основного долга, ПГС – процентная годовая ставка, КДМ – количество дней в месяце, которое варьируется от двадцати восьми до тридцати одного.

Пример № 1. Для примера приведем график платежей при сумме кредита две тысячи условных единиц на срок один год, ежемесячный возврат составляет одну двенадцатую часть кредита и начисленные проценты.Итак, сумма кредита – 2000 единиц, срок кредита – 12 месяцев, процентная ставка – 20%.

№ платежа	Задолженность по кредиту	Начисленные проценты	Сумма основного долга	Сумма очередного платежа
1	2 000	33,33	166,67	200
2	1833,33	30,56	166,67	197,23
3	1666,33	27,77	166,67	194,44
4	1499,66	24,99	166,67	191,66
5	1332,99	22,22	166,67	188,89
6	1166,32	19,43	166,67	186,1
7	999,65	16,66	166,67	183,33
8	832,98	13,88	166,67	180,55
9	666,31	11,11	166,67	177,78
10	499,64	8,33	166,67	175
11	332,97	5,55	166,67	172,22
12	166,67	2,78	166,67	169,45
Итого		216,61	2000	2216,61

Как рассчитываются аннуитетные платежи

Аннуитетными платежами называют платежи, которые выплачиваются равными долями в течение всего кредитного периода, т. е. заемщик регулярно выплачивает платежи одинаковых размеров. Данная сумма меняется по согласованию обеих сторон, либо в случае досрочного погашения. Аннуитетный платеж также включает в себя две части:

Проценты, начисляемые за пользование кредитными средствами.
Сумма основного долга.

При уменьшении сроков кредитования начисляемые проценты снижаются, а сумма основного долга, наоборот, увеличивается. Поначалу основной долг убывает немного медленно. Общий размер всех процентов по долгу значительно больше, что сильно заметно при досрочном погашении кредита. Первые выплаты покрывают большую часть процентов по ссуде.Размеры аннуитетных платежей исчисляются по следующей формуле:

РАП – размер аннуитетного платежа, ПСК – первоначальная сумма кредита, ПГС – процентная годовая ставка, СК – срок кредита.

Такую формулу можно назвать «классической», потому что она применяется во многих банках, электронных таблицах, кредитных калькуляторах.

Пример № 2. Для примера приведем график аннуитетных выплат при кредите в размере одной тысячи условных единиц при сроке в двенадцать месяцев. Итак, сумма кредита – 1000 единиц, сроки кредита – 12 месяцев, годовая процентная ставка – 20%.

№ платежа	Задолженность по кредиту	Начисленные проценты	Сумма основного долга	Сумма очередного платежа
1	1000	75,97	16,67	92,63
2	924,03	77,23	15,4	92,63
3	846,8	78,52	14,11	92,63
4	768,28	79,83	12,8	92,63
5	688,45	81,16	11,47	92,63
6	607,29	82,51	10,12	92,63
7	524,77	83,89	8,75	92,63
8	440,89	85,29	7,35	92,63
9	355,6	86,71	5,93	92,63
10	268,89	88,15	4,48	92,63
11	180,74	89,62	3,01	92,63
12	91,12	91,12	1,52	92,63
Итого		1000	111,61	1111,61

Другие формулы, используемые при расчетах аннуитетных платежей.

Иные организации пользуются формулой, в которой первый платеж не является аннуитетным:

Предварительный платеж не является аннуитетным. Как правило, он включает в себя проценты, начисленные за первый период, полный или неполный. Полный период состоит из тридцати одного дня. В основном, предварительный платеж меньше аннуитетных платежей, однако при долгосрочном кредитовании и высоких процентных ставках он может быть и больше регулярных платежей. Данную формулу применяют в основном в АИЖК.

Также некоторые учреждения применяют формулу, где не только первый, но и последний платеж не аннуитетны:

Первый платеж представляет собой проценты, начисленные за первый период, последний – «хвосты», остатки кредита. Остальные платежи аннуитетные. Остаточный платеж, не аннуитетный. Образуется за счет того, что банковские учреждения подгоняют регулярные платежи под целое число условных единиц. В зависимости от этого последняя выплата может быть как меньше, так и больше регулярных платежей.

Какая схема, дифференцированная или аннуитетная, более выгодна заемщику.

Заемщики довольно часто задумываются, какая схема погашения кредита окажется более выгодной. Если сравнить две схемы, то среди различий можно выделить:

Постоянное убывание суммы платежа при схеме дифференцированной и неизменность суммы при схеме аннуитетной.
При схеме дифференцированной первые платежи несколько велики по сравнению со схемой аннуитетной.
Аннуитетная схема доступна для большинства заемщиков, ведь все выплаты распределяются равномерно на весь срок кредитования. Для выбора дифференцированных платежей доход заемщика должен быть на четверть больше, чем доходы, допустимые при аннуитетной схеме.
Аннуитетная схема предполагает медленное убывание основного долга, повышение начисляемых процентов. При досрочном погашении проценты, выплаченные вперед, будут потеряны. При дифференцированных платежах погашение кредита раньше намеченного срока происходит без больших финансовых потерь.
Добиться начисления выплат по дифференцированной схеме значительно сложнее, потому что заемщик должен обладать большими доходами. Приблизительно можно сказать, что доходы потенциального заемщика должны быть почти на двадцать процентов больше, чем доход, допустимый при аннуитетной схеме начисления.

Итак, вид платежа выступает основным параметром кредита, но рассматривается он только в совокупности с остальными известными параметрами.

Кредитный калькулятор

Использование калькулятора

Используйте этот калькулятор ссуды, чтобы определить ежемесячный платеж, процентную ставку, количество месяцев или основную сумму по кредиту. Найдите свой идеальный платеж, изменив сумму кредита, процентную ставку и срок, и посмотрите, как это повлияет на сумму платежа.

Вы также можете создать и распечатать график погашения ссуды, чтобы увидеть, как ваш ежемесячный платеж будет погашать основную сумму ссуды плюс проценты в течение ссуды.

Сумма кредита: Первоначальная основная сумма новой ссуды или оставшаяся основная сумма по существующей ссуде.
Процентная ставка: Годовая номинальная процентная ставка или заявленная ставка ссуды.
Количество месяцев: Количество платежей, необходимых для погашения кредита.
Ежемесячный платеж: Сумма, подлежащая выплате в счет погашения ссуды при наступлении срока ежемесячного платежа.
Приготовление смеси: Этот калькулятор предполагает, что начисление сложных процентов происходит ежемесячно, как и при выплатах. Для дополнительных возможностей компаундирования используйте наш Расширенный калькулятор ссуды.

Расчет кредита

Когда вы берете ссуду, вы должны выплатить ссуду плюс проценты путем регулярных платежей в банк. Таким образом, вы можете рассматривать ссуду как аннуитет, который вы платите кредитному учреждению.n} \ right] \)

PV — сумма кредита
PMT — ежемесячный платеж
i — месячная процентная ставка в десятичной форме (процентная ставка деленная на 12)
n — количество месяцев (срок кредита в месяцах)

Параметры расчета

Найдите сумму займа

Для расчета суммы кредита используем формулу уравнения кредита в исходном виде:

\ (PV = \ dfrac {PMT} {i} \ left [1- \ dfrac {1} {(1 + i) ^ n} \ right] \)

Пример: Ваш банк предлагает ссуду под 6% годовых, и вы готовы платить 250 долларов в месяц в течение 4 лет (48 месяцев). Какую сумму кредита можно взять?

Решить с помощью калькулятораКалькулятор займа супа

Расчет: Найдите сумму займа
Процентная ставка:% 6
Количество месяцев: 48
Ежемесячный платеж: 250 долларов

Ссылка на ответ: Найдите сумму займа в размере 10 645,08 долларов США.

Решите по формуле:

PMT = 250
п = 48
я = 0.{48}} \ right] \)

= 10 645,08 долл. США

Решите на TI BA II Plus

Убедитесь, что P / Y установлено на 12 для ежемесячных платежей (12 платежей в год и ежемесячное начисление сложных процентов).
Нажмите кнопку [2nd] и [FV], чтобы очистить рабочий лист TVM. n-1} \)

Найдите процентную ставку

Определение процентной ставки — это сложный расчет, включающий Метод Ньютона-Рафсона, о котором вы можете прочитать на сайте MathWorld.

финансовых формул (с калькуляторами)

Люди из всех слоев общества, от студентов, биржевых маклеров и банкиров; риэлторам, домовладельцам и управляющим находят финансовые формулы невероятно полезными в повседневной жизни. Используете ли вы финансовые формулы для личных или по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь.

Независимо от того, в какой финансовой сфере вы работаете или изучаете, от корпоративных финансов до банковского дела, все они построены на тот же фундамент стандартных формул и уравнений. Хотя некоторые из этих сложных формул могут сбить с толку обычного человека, мы помочь, внося вам ясность.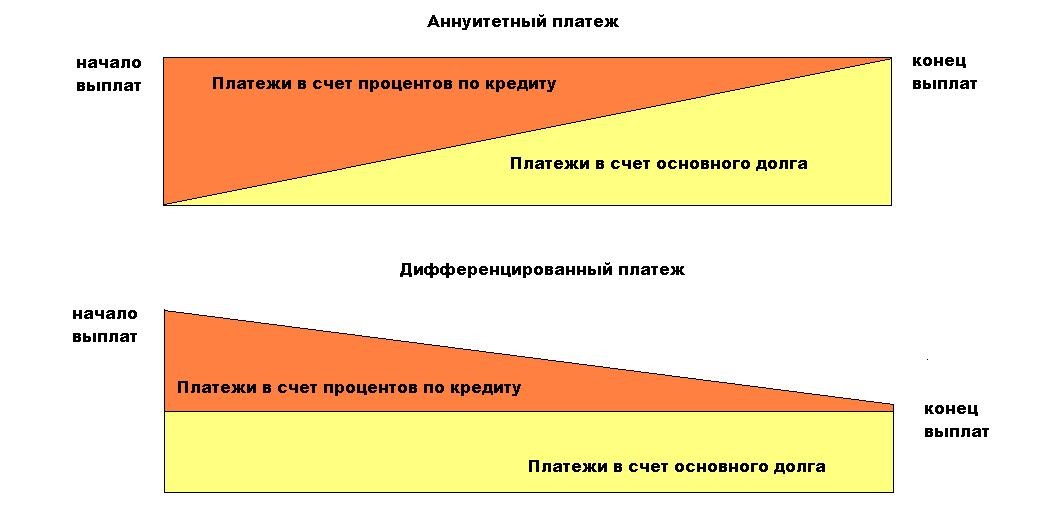

Имеете ли вы дело со сложными процентами, аннуитетами, акциями или облигациями, инвесторы должны иметь возможность эффективно оценивать уровень ценности или достоинства их финансовых показателей.Это делается путем оценки будущей прибыли и ее расчета относительно текущая стоимость или эквивалентная норма прибыли.

FinanceFormulas.net может помочь.

Финансовая информация и калькуляторы на сайте FinanceFormulas.net предназначены не только для профессионалов, но и для всех, кто потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа которые изучают финансы и бизнес, для профессионалов, занимающихся корпоративными финансами, FinanceFormulas.сеть поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха.

Кто может получить больше всего от FinanceFormulas. net?

Студенты, изучающие финансы и бизнес, могут использовать формулы и калькуляторы, бесплатно предоставляемые FinanceFormulas.net в качестве постоянного справочника, во время учебы в школе, затем во время работы в мир финансов.

Люди, уже работающие в сфере бизнеса , которые могут иметь Если вы забыли, как использовать конкретную формулу или набор уравнений, наши инструменты станут бесценным ресурсом.FinanceFormulas.net не только упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы больше никогда не придется тратить время на поиск нужного инструмента.

Любой . Люди любого возраста могут пользоваться калькуляторами в FinanceFormulas.net, чтобы помочь им справляться с финансовыми трудностями повседневной жизни. Ипотека, задолженность по кредитной карте или понимание академической оценки вашего инвестиции, такие как акции и облигации, он имеет доступ к правильным формулам, уравнениям и калькуляторам, которые могут помочь вам проложите свой путь к финансово благополучной жизни.

Планируете ли вы использовать бесплатные формулы, предоставляемые FinanceFormulas.net, для личного или академического использования, FinanceFormulas.net здесь, чтобы помочь вам найти банковские формулы, формулы акций и облигаций, корпоративные и прочие формулы, которые вам нужны.

Вернуться к началу

Финансовый калькулятор

Этот финансовый калькулятор можно использовать для расчета любого количества следующих параметров: будущая стоимость (FV), количество периодов начисления сложных процентов (N), процентная ставка (I / Y), аннуитетный платеж (PMT) и начальная основная сумма, если другие параметры известны.На каждой из следующих вкладок представлены параметры, которые необходимо вычислить.

Результаты

FV (будущая стоимость)	48 997,75 долл. США
PV (текущая стоимость)	27 360,09 долл. США
N (количество периодов)	10.000
10.000
6.000%
PMT (Периодический платеж)	1000,00 долларов США
Начальные инвестиции	20000 долларов США.00
Общая сумма основного долга	30 000,00 долларов США
Общая сумма процентов	18 997,75 долларов США

График накопления сальдо

График

1,000

	начальная основная сумма	начальный баланс	проценты	конечный баланс	конечная основная сумма
		00	$ 20,000. 00	$ 1,200.00	$ 22,200.00	$ 21,000.00
2	$ 21,000.00	$ 22,200.00	$ 1,332.00	$ 24,532.00	$ 22,000.00
3	$ 22,000.00	$ 24,532.00	$ 1,471.92	$ 27,003.92	23 000,00 долл.
4	23 000,00 долл.	27 003,92 долл. США	1 620,24 долл. США	29 624 долл. США.16	$ 24,000.00
5	$ 24,000.00	$ 29,624.16	$ 1,777.45	$ 32,401.60	$ 25,000.00
6	$ 25,000.00	$ 32,401.60	$ 1,944.10	$ 35,345.70	$ 26,000.00
7	26 000,00 долл.	35 345,70 долл. США	2 120,74 долл. США	38 466,44 долл. США	27 000,00 долл. США
8	27 000 долл. США.00	$ 38,466.44	$ 2,307.99	$ 41,774.43	$ 28,000.00
9	$ 28,000.00	$ 41,774.43	$ 2,506.47	$ 45,280.90	$ 29,000.00
10	$ 29,000.00	$ 45,280.90	$ 2,716.85	$ 48,997.75	$ 30,000.00

Калькулятор связанного кредита | Калькулятор процентов | Ипотечный калькулятор

На базовых курсах финансов много времени уходит на расчет временной стоимости денег, который может включать 4 или 5 различных элементов, включая текущую стоимость (PV), будущую стоимость (FV), процентную ставку (I / Y) и количество периодов (N).Аннуитетный платеж (PMT) может быть включен, но не является обязательным элементом.

Временная стоимость денег

Предположим, кто-то должен вам 500 долларов. Вы бы предпочли, чтобы эти деньги были возвращены вам сразу же одним платежом или распределены в течение года четырьмя платежами в рассрочку? Что бы вы почувствовали, если бы вам пришлось ждать полной оплаты вместо того, чтобы получать ее сразу? Разве вы не почувствуете, что просрочка платежа вам чего-то стоит?

В соответствии с концепцией, которую экономисты называют «временной стоимостью денег», вы, вероятно, захотите сразу все деньги, потому что их можно сразу же использовать для самых разных целей: потратить на роскошный отпуск своей мечты, инвестировать, чтобы заработать проценты, или использовать чтобы полностью или частично погасить ссуду.«Временная стоимость денег» относится к тому факту, что доллар в руках сегодня стоит больше, чем доллар, обещанный в будущем.

Это основа концепции процентных выплат; Хороший пример — когда деньги кладутся на сберегательный счет, получаются небольшие дивиденды за то, что деньги остаются в банке; финансовое учреждение платит небольшую цену за наличие этих денег. По этой же причине банк будет платить больше за более длительное хранение денег и за фиксирование их там на фиксированные периоды.

Это увеличение стоимости денег в конце периода взимания процентов называется будущей стоимостью в финансах. Вот как это работает.

Предположим, что 100 долларов (PV) инвестируются на сберегательный счет, на который выплачивается 10% годовых (I / Y) в год. Сколько будет через год? Ответ — 110 долларов (FV). Эти 110 долларов равны первоначальной основной сумме 100 долларов плюс 10 долларов процентов. 110 долларов — это будущая стоимость 100 долларов, инвестированных в течение одного года под 10%. Это означает, что 100 долларов сегодня стоят 110 долларов через год при условии, что процентная ставка составляет 10%.

Как правило, инвестирование в течение одного периода с процентной ставкой r вырастет до (1 + r) на каждый вложенный доллар. В нашем примере r составляет 10%, поэтому инвестиции вырастут до:

1 + 0,10 = 1,10

1,10 доллара за каждый вложенный доллар. Поскольку в этом случае было инвестировано 100 долларов, результат, или FV, составляет:

100 долларов США × 1,10 = 110

долларов США

Первоначальные инвестиции в размере 100 долларов теперь составляют 110 долларов. Однако, если эти деньги будут храниться на сберегательном счете и дальше, какой будет полученная справедливая стоимость через два года при условии, что процентная ставка останется прежней?

110 × 0.10 = 11

долларов США

11 долларов США будут начислены в виде процентов после второго года, в результате чего в общей сложности будет:

110 + 11 = 121

121 доллар — это будущая стоимость 100 долларов через два года под 10%.

Кроме того, PV в финансах — это то, что будет стоить FV с учетом ставки дисконтирования, которая имеет то же значение, что и процентная ставка, за исключением того, что применяется обратно пропорционально времени (в обратном, а не в прямом направлении. В этом примере PV FV равной 121 доллар со ставкой дисконта 10% после 2 периодов начисления сложных процентов (N) составляет 100 долларов.

Денежная структура этого FV на $ 121 состоит из нескольких частей:

Первая часть — это первая первоначальная основная сумма в 100 долларов или ее текущая стоимость (PV)
Вторая часть — это 10 долларов процентов, полученных в первый год.
Третья часть — это остальные 10 долларов США по процентам, полученным во второй год.
Четвертая часть — 1 доллар, который представляет собой проценты, полученные во второй год по процентам, выплаченным в первый год: (10 долларов × 0,10 = 1 доллар)

PMT

PMT или аннуитетный платеж — это сумма притока или оттока, которая происходит в каждый период начисления сложных процентов финансового потока.Возьмем, к примеру, арендуемую недвижимость, которая приносит доход от аренды в размере 1000 долларов в месяц, постоянный денежный поток. Инвесторы могут задаться вопросом, сколько стоит денежный поток в размере 1000 долларов в месяц в течение 10 лет, в противном случае у них нет убедительных доказательств того, что они должны вкладывать такие деньги в арендуемую недвижимость. В качестве другого примера, как насчет оценки бизнеса, приносящего 100 долларов дохода в год? А как насчет выплаты первоначального взноса в размере 30 000 долларов и ежемесячной ипотеки в размере 1 000 долларов? Для этих вопросов формула оплаты довольно сложна, поэтому лучше оставить ее в руках нашего финансового калькулятора, который может помочь оценить все эти ситуации с включением функции PMT.Не забудьте выбрать правильный ввод для того, производятся ли выплаты в начале или в конце периодов начисления сложных процентов; выбор имеет большое значение для окончательной суммы процентов.

Финансовый класс

Для любого студента, изучающего бизнес, будет чрезвычайно сложно ориентироваться в курсах финансов без удобного финансового калькулятора. Хотя большинство основных финансовых расчетов технически можно выполнить вручную, профессора обычно позволяют студентам использовать финансовые калькуляторы даже во время экзаменов.Важна не способность выполнять вычисления вручную; это понимание финансовых концепций и того, как их применять с помощью этих удобных вычислительных инструментов, которые были изобретены. Наш веб-финансовый калькулятор может служить хорошим инструментом для использования во время лекций или выполнения домашних заданий, а поскольку он основан на веб-интерфейсе, он всегда под рукой, пока рядом находится смартфон. Включение графика накопления баланса, графика амортизации и круговой диаграммы с разбивкой основной суммы и процентов, двух вещей, отсутствующих в физических калькуляторах, может быть более визуально полезным для целей обучения.

Важность финансового калькулятора

По сути, наш финансовый калькулятор является основой большинства наших финансовых калькуляторов. Это помогает думать о нем как об эквиваленте парового двигателя, который в конечном итоге использовался для питания самых разных вещей, таких как пароход, железнодорожные локомотивы, фабрики и дорожные транспортные средства. Не может быть ипотечного калькулятора, калькулятора кредитных карт или автокредитного калькулятора без концепции временной стоимости денег, как объясняется Финансовым калькулятором. По сути, наш инвестиционный калькулятор — это просто ребрендинг финансового калькулятора, в то время как все, что скрывается под капотом, по сути то же самое. Начальный принцип просто переименован в «Начальная сумма», FV — «Конечная сумма», N — «Инвестиционная длина» и так далее.

аннуитетов и ссуд — Math For Our World

Результаты обучения

Расчет остатка аннуитета по истечении определенного периода времени
Различие между сложными процентами, аннуитетом и выплатой аннуитета с учетом финансового сценария
Используйте формулу ссуды для расчета выплат по ссуде, остатка ссуды или начисленных процентов по ссуде
Определите, какое уравнение использовать для данного сценария
Решите финансовую заявку на время

По мнению большинства из нас, сегодня мы не можем положить крупную сумму денег в банк.Вместо этого мы откладываем на будущее, вкладывая в банк меньшую сумму денег с каждой зарплаты. В этом разделе мы рассмотрим математику, лежащую в основе определенных типов счетов, которые со временем вызывают интерес, например пенсионных счетов. Мы также рассмотрим, как рассчитываются ипотечные кредиты и автокредиты, называемые ссудой в рассрочку.

Сберегательные аннуитеты

По мнению большинства из нас, сегодня мы не можем положить крупную сумму денег в банк. Вместо этого мы откладываем на будущее, вкладывая в банк меньшую сумму денег с каждой зарплаты.Эта идея называется сберегательным аннуитетом . Большинство пенсионных планов, таких как планы 401k или планы IRA, являются примерами сберегательных аннуитетов.

Аннуитет можно описать рекурсивно довольно просто. Напомним, что базовый сложный процент следует из соотношения

Для сберегательного аннуитета нам просто нужно добавлять депозит d на счет с каждым периодом начисления сложных процентов:

Преобразовать это уравнение из рекурсивной формы в явную немного сложнее, чем при использовании сложных процентов. В этом легче всего убедиться, работая на примере, а не работая в целом.

Пример

Предположим, мы будем вносить 100 долларов каждый месяц на счет с выплатой 6% годовых. Мы предполагаем, что счет пополняется с той же периодичностью, с которой мы делаем депозиты, если не указано иное. Напишите явную формулу, представляющую этот сценарий.

Решение:

В этом примере:

r = 0,06 (6%)
k = 12 (12 соединений / отложений в год)
d = 100 $ (наш депозит в месяц)

Запись рекурсивного уравнения дает

Предполагая, что мы начинаем с пустой учетной записи, мы можем начать использовать это соотношение:

Продолжая эту схему, после м залежей мы сэкономили бы:

Другими словами, через млн месяцев, по первому депозиту будут начислены сложные проценты на сумму млн — 1 месяц. По второму депозиту будут начислены проценты на млн. -2 месяца. Депозит за последний месяц (L) принес бы проценты только за один месяц. По последнему депозиту проценты еще не начисляются.

Однако это уравнение оставляет желать лучшего — оно не упрощает расчет конечного баланса! Чтобы упростить задачу, умножьте обе части уравнения на 1,005:

Распределение в правой части уравнения дает

Теперь мы сопоставим это с аналогичными членами из нашего исходного уравнения и вычтем каждую сторону

(1)

Почти все члены сокращаются в правой части при вычитании, оставляя

Выносим за скобки термины в левой части.

Решить для P _m

(2)

Замена м месяцев на 12 N , где N измеряется в годах, дает

Отзыв 0,005 был р / к , а 100 — залог дн. 12 было к , количество депозита каждый год.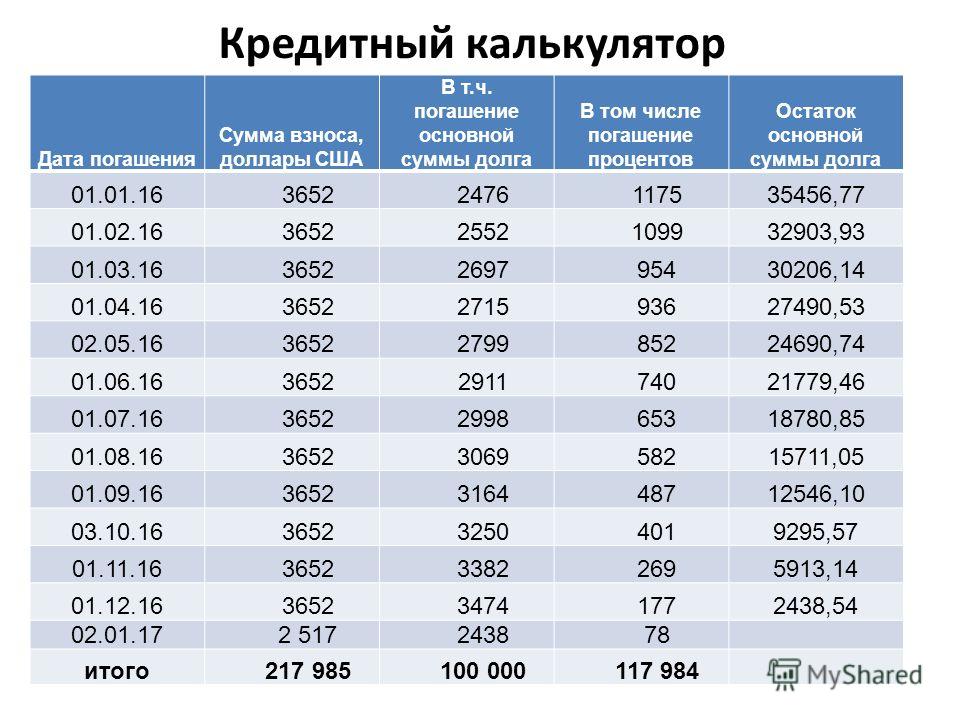

Обобщая этот результат, получаем формулу ренты сбережений.

Формула аннуитета

P _N — остаток на счете после N лет.
d — обычный депозит (сумма, которую вы вносите каждый год, каждый месяц и т. Д.)
r — годовая процентная ставка в десятичной форме.
k — количество периодов начисления сложных процентов в году.

Если частота начисления сложных процентов не указана явно, предположим, что количество соединений в году равно количеству депозитов, сделанных за год.

Например, если не указана частота начисления процентов:

Если вы делаете вклады каждый месяц, используйте ежемесячное начисление процентов, k = 12.
Если вы делаете депозиты каждый год, используйте годовое начисление процентов, k = 1.
Если вы делаете вклады каждый квартал, используйте квартальное начисление сложных процентов, k = 4.
и т. Д.

Когда вы это используете?

Аннуитеты предполагают, что вы кладете деньги на счет на регулярной основе (каждый месяц, год, квартал и т. Д.) И позволяете ему оставаться там, зарабатывая проценты.

Сложные проценты предполагает, что вы кладете деньги на счет один раз и позволяете им оставаться там, зарабатывая проценты.

Сложные проценты: Один депозит
Аннуитет: много депозитов.

Примеры

Традиционный индивидуальный пенсионный счет (IRA) — это особый тип пенсионного счета, на который вкладываемые вами деньги освобождаются от налога на прибыль до тех пор, пока вы их не снимете. Если вы вносите 100 долларов в месяц в IRA с доходом 6%, сколько у вас будет на счете через 20 лет?

Решение:

В этом примере

d = 100 долларов	ежемесячный депозит
r = 0.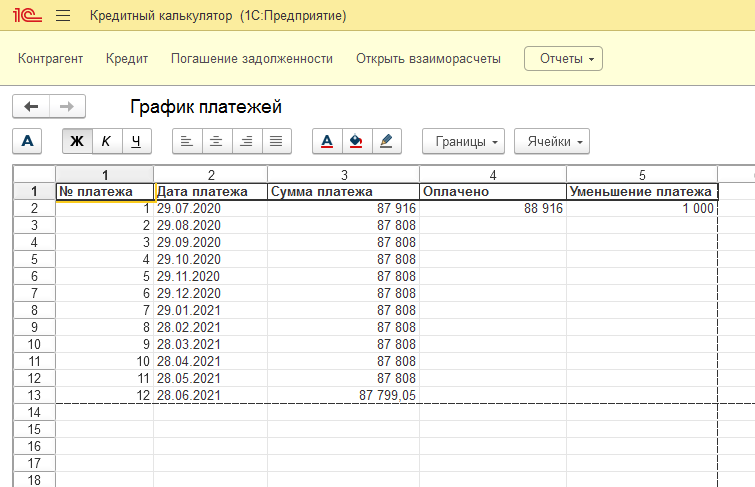 06	6% годовых
к = 12	, поскольку мы делаем ежемесячные вклады, мы будем складывать ежемесячно
N = 20	мы хотим сумму через 20 лет

Подставляя это в уравнение:

(Обратите внимание, что мы умножили N раз на k перед тем, как поместить его в экспоненту. Это простое вычисление, которое упростит ввод в Desmos:

Счет вырастет до 46 204 долларов.09 через 20 лет.

Обратите внимание, что вы внесли на счет в общей сложности 24 000 долларов (100 долларов в месяц в течение 240 месяцев). Разница между тем, что вы получаете в итоге, и тем, сколько вы вкладываете, — это заработанные проценты. В данном случае это 46 204,09 доллара — 24 000 = 22 204,09 доллара.

Этот пример подробно объясняется здесь. Обратите внимание, что каждая часть была проработана отдельно и округлена. Ответ выше, где мы использовали Desmos, более точен, поскольку округление было оставлено до конца. Вы можете решить проблему в любом случае, но обязательно просмотрите видео ниже, которое достаточно округлено для получения точного ответа.

Попробуй

Консервативный инвестиционный счет приносит 3% годовых. Если вы будете вносить на этот счет 5 долларов в день, сколько у вас будет через 10 лет? Сколько с процентов?

Решение:

д = 5 $ ежедневный депозит

r = 0,03 3% годовая ставка

k = 365, так как мы делаем ежедневные депозиты, мы ежедневно добавляем

N = 10 нам нужна сумма через 10 лет

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Специалисты по финансовому планированию обычно рекомендуют вам накопить определенную сумму сбережений после выхода на пенсию. Если вам известна будущая стоимость счета, вы можете рассчитать сумму ежемесячного взноса, которая даст вам желаемый результат. В следующем примере мы покажем вам, как это работает.

Пример

Вы хотите, чтобы на вашем счету было 200 000 долларов, когда вы выйдете на пенсию через 30 лет. Ваш пенсионный счет приносит 8% годовых. Сколько вам нужно вкладывать каждый месяц, чтобы достичь своей пенсионной цели?

В этом примере мы ищем d .

r = 0,08	8% годовых
к = 12	, поскольку мы вносим ежемесячно
N = 30	30 лет
P30 = 200 000 долларов США	Сумма, которую мы хотим иметь через 30 лет

В этом случае нам нужно будет составить уравнение и решить относительно d .

(3)

Итак, вам нужно будет внести 134 доллара.09 каждый месяц, чтобы иметь 200 000 долларов через 30 лет, если ваш счет приносит 8% годовых.

Посмотрите на решение этой проблемы в следующем видео.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Аннуитеты на выплату

Удаление денег из ренты

В последнем разделе вы узнали об аннуитетах. При аннуитете вы начинаете с нуля, регулярно кладете деньги на счет и в конечном итоге получаете деньги на своем счете.

В этом разделе мы узнаем об изменении под названием Payout Annuity . При выплате аннуитета вы начинаете с денег на счете и регулярно снимаете деньги со счета. Любые оставшиеся на счете деньги приносят проценты. По прошествии определенного времени аккаунт станет пустым.

Аннуитеты на выплату обычно используются после выхода на пенсию. Возможно, вы накопили 500 000 долларов для выхода на пенсию и хотите ежемесячно снимать деньги со счета, чтобы жить.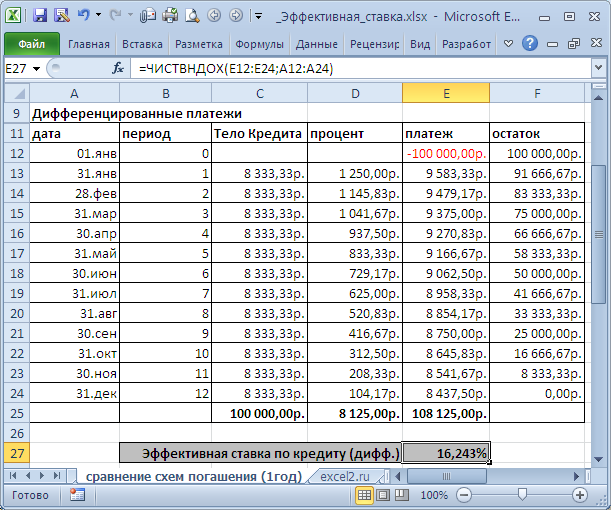 Вы хотите, чтобы денег хватило на 20 лет. Это аннуитет на выплату. Формула выводится таким же образом, как и для сберегательных аннуитетов. Подробности здесь не приводятся.

Формула выплаты аннуитета

P ₀ — это остаток на счете в начале (начальная сумма или основная сумма).
d — это обычное снятие (сумма, которую вы снимаете каждый год, каждый месяц и т. Д.)
r — годовая процентная ставка (в десятичной форме.Пример: 5% = 0,05)
k — количество периодов начисления сложных процентов в году.
N — количество лет, в течение которых мы планируем снимать средства

Как и в случае с аннуитетами, частота начисления сложных процентов не всегда явно указывается, а определяется тем, как часто вы снимаете средства.

Когда вы это используете?

Аннуитеты на выплату предполагают, что вы снимаете деньги со счета регулярно (каждый месяц, год, квартал и т. Д.)), а остальные пусть сидят и зарабатывают проценты.

Сложные проценты: Один депозит
Аннуитет: много депозитов.
Аннуитет на выплату: много выводов

Пример

После выхода на пенсию вы хотите иметь возможность получать 1000 долларов каждый месяц в течение 20 лет со своего пенсионного счета. Счет приносит 6% годовых. Сколько вам понадобится на вашем счете после выхода на пенсию?

В этом примере

d = 1000 долларов США	ежемесячный вывод
r = 0.06	6% годовых
к = 12	, так как мы ежемесячно снимаем средства, мы добавляем ежемесячно
N = 20	с тех пор, как снимали деньги в течение 20 лет

Мы ищем P _0: , сколько денег должно быть на счете в начале.

Подставляя это в уравнение:

(4)

Когда вы выйдете на пенсию, на вашем счету будет 139 600 долларов.

Вышеупомянутая проблема решалась по частям, но помните, что вы можете решить всю задачу сразу в своем калькуляторе Desmos и избежать округления.

Обратите внимание, что вы сняли в общей сложности 240 000 долларов (1000 долларов в месяц в течение 240 месяцев). Разница между тем, что вы вытащили, и тем, с чего вы начали, — это заработанные проценты. В данном случае это 240 000 — 139 600 долларов = 100 400 долларов процентов.

Узнайте больше об этой проблеме в этом видео.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Вычисление отрицательных показателей на вашем калькуляторе

С этими задачами вам нужно возвести числа в отрицательную степень. В большинстве калькуляторов есть отдельная кнопка для отрицания числа, которое отличается от кнопки вычитания. Некоторые калькуляторы обозначают это (-), некоторые — +/-. Кнопка часто находится рядом с клавишей = или десятичной точкой.

Если на вашем калькуляторе отображаются операции (обычно это калькулятор с многострочным дисплеем), для вычисления 1.(-) 240

Если ваш калькулятор показывает только одно значение за раз, то обычно вы нажимаете клавишу (-) после числа, чтобы отрицать его, поэтому вы набираете: 1,005 yx 240 (-) =

Попробуйте — у вас должно получиться 1,005 ^-240 = 0,302096

Пример

Вы знаете, что после выхода на пенсию на вашем счету будет 500 000 долларов. Вы хотите иметь возможность ежемесячно снимать средства со счета в течение 30 лет. Ваш пенсионный счет приносит 8% годовых. Сколько вы сможете снимать каждый месяц?

В этом примере мы ищем d .

r = 0,08	8% годовых
к = 12	, поскольку мы снимаем ежемесячно
N = 30	30 лет
P ₀ = 500 000 долларов США	начинаем с 500 000 $

В этом случае нам нужно будет составить уравнение и решить относительно d .

(5)

Вы сможете вывести 3 670 долларов.21 каждый месяц в течение 30 лет.

Подробное описание этого примера можно посмотреть здесь.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Попробуй

Донор дает 100 000 долларов университету и указывает, что они будут использоваться для выплаты ежегодных стипендий на следующие 20 лет. Если университет может зарабатывать 4% годовых, сколько они могут выплачивать стипендии каждый год?

d = неизвестно

r = 0.04 4% годовая ставка

k = 1, так как мы выплачиваем ежегодные стипендии

N = 20 20 лет

P0 = 100 000, мы начинаем со 100 000 долларов США

Решение для d дает 7 358,18 долларов в год, которые они могут предоставить в качестве стипендий.

Стоит отметить, что обычно доноры вместо этого указывают, что на стипендию должны быть потрачены только проценты, в результате чего первоначальное пожертвование действует бесконечно.Если бы этот донор указал это, было бы доступно 100000 долларов (0,04) = 4000 долларов в год.

Кредиты

Обычные ссуды

В последнем разделе вы узнали об аннуитетах на выплаты. В этом разделе вы узнаете об обычных кредитах (также называемых амортизированными кредитами или кредитами в рассрочку). Примеры включают автокредиты и жилищную ипотеку. Эти методы не применимы к ссудам до зарплаты, дополнительным ссудам или другим типам ссуд, когда проценты начисляются заранее.

В ссудах замечательно то, что они используют ту же формулу, что и аннуитет на выплату. Чтобы понять, почему, представьте, что вы вложили 10 000 долларов в банк и начали принимать платежи, одновременно получая проценты в рамках выплаты аннуитета, и через 5 лет ваш баланс стал нулевым. Переверните это и представьте, что вы действуете как банк, а автомобильный кредитор действует как вы. Автокредитор инвестирует в вас 10 000 долларов. Поскольку вы действуете как банк, вы платите проценты. Автокредитор принимает платежи до тех пор, пока баланс не станет нулевым.

Формула займа

P ₀ — это остаток на счете в начале (основная сумма или сумма ссуды).
d — ваш платеж по кредиту (ежемесячный платеж, годовой платеж и т. Д.)
r — годовая процентная ставка в десятичной форме.
k — количество периодов начисления сложных процентов в году.
N — срок кредита в годах.

Как и раньше, частота начисления сложных процентов не всегда указывается явно, а определяется тем, как часто вы производите платежи.

Когда вы это используете?

Формула ссуды предполагает, что вы производите выплаты по ссуде по регулярному графику (каждый месяц, год, квартал и т. Д.) И платите проценты по ссуде.

Сложные проценты: Один депозит
Аннуитет: много депозитов
Аннуитет на выплату: много выводов
Кредиты: много платежей

Пример

Вы можете позволить себе 200 долларов в месяц в качестве оплаты машины. Если вы можете получить автокредит под 3% годовых на 60 месяцев (5 лет), сколько денег вы можете себе позволить? Другими словами, на какую сумму кредита вы можете погасить 200 долларов в месяц?

В этом примере

d = 200 долларов США	ежемесячный платеж по кредиту
r = 0,03	3% годовых
к = 12	, так как мы делаем ежемесячные платежи, мы будем складывать ежемесячно
N = 5	, так как мы делаем ежемесячные платежи за 5 лет

Мы ищем P ₀ , начальную сумму кредита.

(6)

Вы можете позволить себе ссуду в размере 11 120 долларов.

Вы заплатите кредитной компании в общей сложности 12 000 долларов (200 долларов в месяц в течение 60 месяцев). Разница между суммой, которую вы платите, и суммой кредита — это уплаченные проценты. В этом случае вы платите 12 000–11 120 долларов США = общая сумма процентов 880 долларов США.

Подробности этого примера рассмотрены в этом видео.

Щелкните здесь, чтобы просмотреть это видео.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Пример

Вы хотите получить ипотечный кредит на сумму 140 000 долларов США. Процентная ставка по кредиту составляет 6%, срок кредита — 30 лет. Сколько будут ваши ежемесячные платежи?

Решение:

В этом примере мы ищем d .

r = 0,06	6% годовых
к = 12	, так как мы платим ежемесячно
N = 30	30 лет
P ₀ = 140 000 долларов США	начальная сумма кредита

В этом случае нам нужно будет составить уравнение и решить относительно d .

(7)

Вы будете платить 839,37 долларов в месяц в течение 30 лет.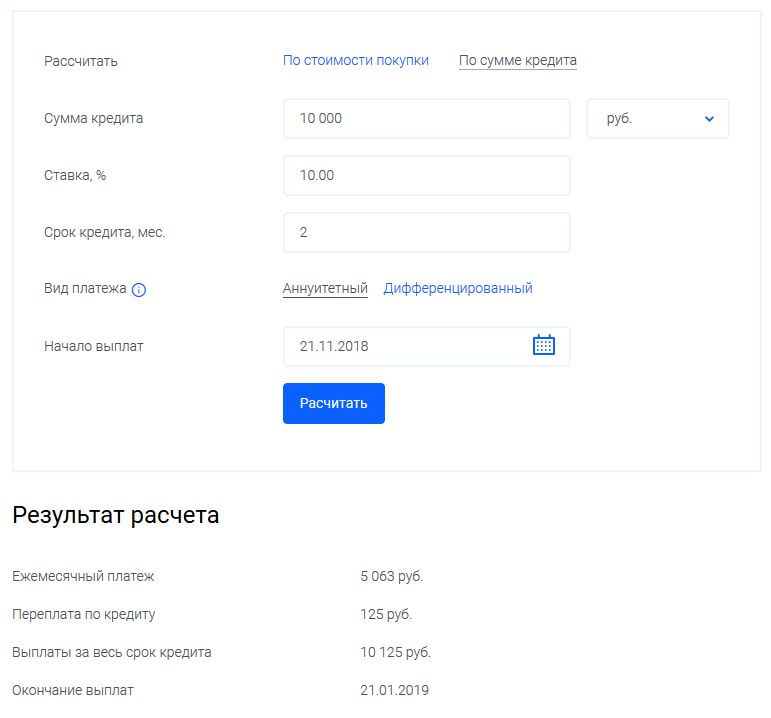

Вы платите кредитной компании 302 173,20 доллара США: 839,37 доллара США в месяц в течение 360 месяцев. Вы платите в общей сложности 302 173,20 долл. США — 140 000 долл. США = 162 173,20 долл. США в виде процентов в течение срока действия кредита.

Подробнее об этом примере можно узнать здесь.

Попробуй

Щелкните здесь, чтобы попробовать решить эту проблему.

Попробуй

Жанин купила новую мебель на 3000 долларов в кредит.Поскольку у нее не очень хороший кредитный рейтинг, магазин взимает с нее довольно высокую процентную ставку по кредиту: 16%. Если она согласилась оплачивать мебель в течение 2 лет, сколько ей придется платить каждый месяц?

Решение:

d = неизвестно

r = 0,16 16% годовая ставка

k = 12, так как мы делаем ежемесячные платежи

N = 2 2 года до погашения

P0 = 3000, мы начинаем с кредита на 3000 долларов

Решите вопрос d, чтобы получить ежемесячные выплаты в размере 146 долларов США. 89

Два года до погашения означают 146,89 долларов (24) = 3525,36 долларов в общей сумме выплат. Это означает, что Джанин заплатит 3525,36 доллара — 3000 = 525,36 доллара в виде процентов.

Расчет баланса

В случае ссуды часто бывает желательно определить, какой будет остаток по ссуде через некоторое количество лет. Например, если вы покупаете дом и планируете продать его через пять лет, вы можете узнать, какую часть остатка по кредиту вы выплатите и сколько вам придется заплатить в результате продажи.

Чтобы определить остаток ссуды через некоторое количество лет, нам сначала нужно знать платежи по ссуде, если мы еще не знаем их. Помните, что только часть ваших платежей по кредиту идет на баланс ссуды; часть идет на проценты. Например, если ваши платежи составляли 1000 долларов в месяц, через год вы будете , а не , которые выплатят 12000 долларов из остатка ссуды.

Чтобы определить остаток ссуды, мы можем подумать, «сколько ссуды смогут погасить эти платежи по ссуде в оставшееся время по ссуде?»

Пример

Если по ипотеке с процентной ставкой 6% предусмотрены выплаты в размере 1000 долларов в месяц, сколько будет остаток по ссуде через 10 лет после окончания ссуды?

Решение:

Чтобы определить это, мы ищем сумму ссуды, которая может быть погашена ежемесячными платежами в размере 1000 долларов в течение 10 лет. Другими словами, мы ищем P ₀, когда

d = 1000 долларов США	ежемесячный платеж по кредиту
r = 0,06	6% годовых
к = 12	, так как мы делаем ежемесячные платежи, мы будем складывать ежемесячно
N = 10	, поскольку мы делаем ежемесячные платежи еще на 10 лет

(8)

Остаток кредита, оставшийся до 10 лет, составит 90 073 долларов.45.

Этот пример объясняется в этом видео:

Часто для ответа на вопросы об остатке баланса требуется два шага:

Расчет ежемесячных платежей по кредиту
Расчет остатка ссуды на основе оставшегося времени по ссуде

Пример

Пара покупает дом по ипотеке в размере 180 000 долларов под 4% на 30 лет с ежемесячными платежами. Какой будет остаток по ипотеке через 5 лет?

Решение:

Сначала посчитаем их ежемесячные выплаты.

Ищем d .

r = 0,04	4% годовых
к = 12	, поскольку они платят ежемесячно
N = 30	30 лет
P ₀ = 180000 долларов США	начальная сумма кредита

Мы составляем уравнение и решаем относительно d .

(9)

Теперь, когда мы знаем ежемесячные платежи, мы можем определить остаток.Нам нужен остаток через 5 лет, когда по ссуде останется 25 лет, поэтому мы рассчитываем остаток по ссуде, который будет выплачен ежемесячными платежами в течение этих 25 лет.

d = 858,93 долл. США	ежемесячный платеж по кредиту, рассчитанный нами выше
r = 0,04	4% годовых
к = 12	, поскольку они делают ежемесячные платежи
N = 25	, поскольку они будут производить ежемесячные выплаты еще 25 лет

(10)

Остаток ссуды через 5 лет, когда до конца ссуды осталось 25 лет, составит 155 793 доллара. 91.

За эти 5 лет пара выплатила 180 000 долларов — 155 793,91 доллара = 24 206,09 доллара из остатка по кредиту. В течение 5 лет (60 месяцев) они платили в общей сложности 858,93 доллара в месяц, что в сумме составляет 51 535,80 доллара, так что 51 535,80 доллара — 24 206,09 доллара = 27 329,71 доллара из того, что они заплатили до сих пор, были процентами.

Дополнительное объяснение этого примера доступно здесь:

FYI

Жилищные ссуды обычно выплачиваются в процессе амортизации, амортизация относится к погашению долга (часто по ссуде или ипотеке) с течением времени посредством регулярных платежей.График погашения представляет собой таблицу , в которой подробно описывается каждый периодический платеж по погашаемой ссуде , генерируемый калькулятором амортизации .

Если вы хотите узнать больше, нажмите на ссылку ниже, чтобы перейти на веб-сайт «Как рассчитывается график амортизации?» пользователя MyAmortizationChart. com. На этом веб-сайте представлен краткий обзор графиков амортизации.

Щелкните здесь, чтобы попробовать решить эту проблему.

Аннуитетный платеж | Формула, пример, заключение, калькулятор

Аннуитет — это финансовый продукт, который выплачивает серию денежных потоков с определенной периодичностью и в течение фиксированного периода времени.Период выплаты аннуитета может быть ежегодно, два раза в год, ежеквартально и ежемесячно. Зная процентную ставку и количество периодов времени, вы можете рассчитать как настоящую, так и будущую стоимость аннуитета.

Обычно существует два типа аннуитета: обычная аннуитетная и аннуитетная. Обычный аннуитет требует выплаты в конце каждого периода. Например, по прямым облигациям выплата купона обычно производится в конце каждых шести месяцев до погашения. Причитающиеся платежи по аннуитету требуются в начале каждого периода, например, ваша арендная плата считается подлежащей выплате, поскольку она выплачивается при первом въезде, а затем обычно в начале каждого месяца. {-n}} {r} \ bigg]

C = денежный поток за период
r = процентная ставка
n = количество платежей

Проще говоря, приведенная стоимость аннуитета — это текущая стоимость доход, который будет получен от инвестиций в будущем, и он основан на концепции временной стоимости денег, которая утверждает, что доллар сегодня более ценен, чем доллар, заработанный в будущем.

Если вы знаете, сколько вы можете инвестировать для каждого платежа в течение фиксированного периода времени, вы также можете рассчитать будущую стоимость (FV) аннуитета, чтобы узнать, сколько у вас будет в будущем.{n} — 1} {r} \ bigg]

Эта формула упрощает расчет будущей стоимости для большого количества денежных потоков и действует как ярлык для нахождения совокупной стоимости всех денежных потоков, полученных от аннуитета.

Пример аннуитета

Допустим, у вас есть аннуитет, который выплачивает денежный поток в размере 1000 долларов каждый год в течение следующих пяти лет, и вы вкладываете каждый платеж под 5% процентной ставки.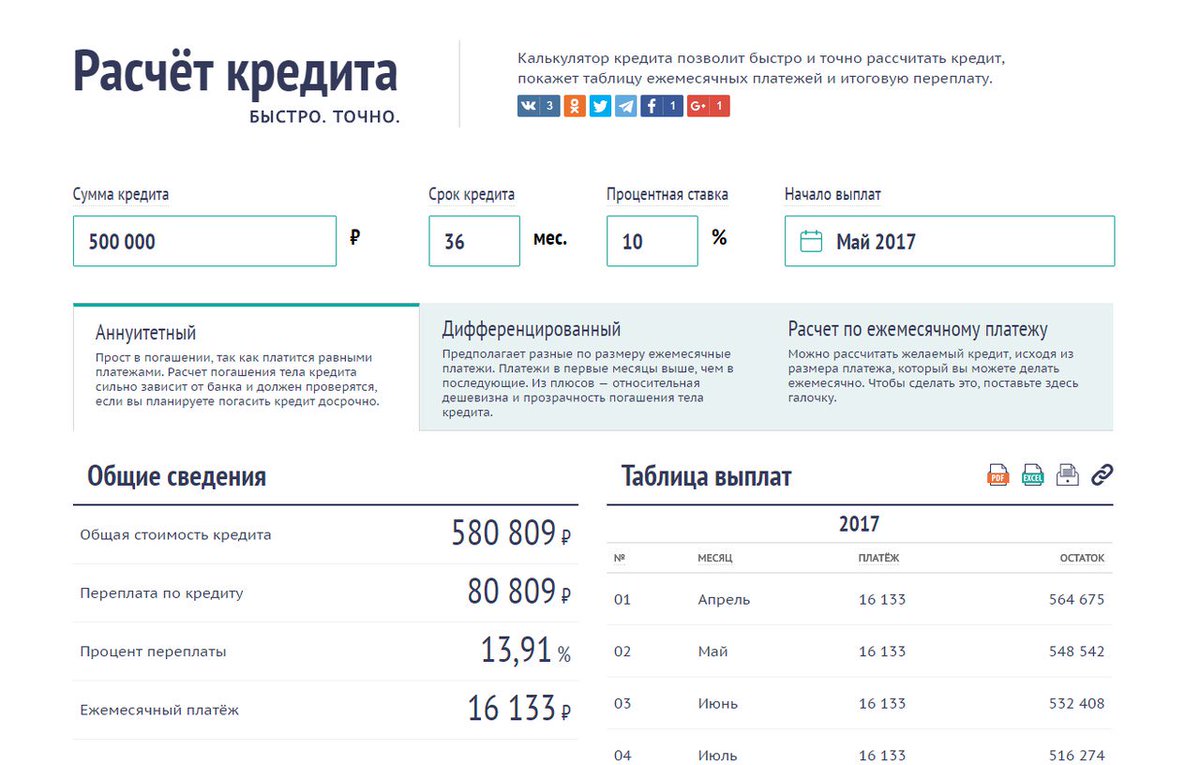 {- 5}} {5 \%} \ bigg] = \ $ 4 {,} 329.{5} — 1} {5 \%} \ bigg] = \ $ 5 {,} 525,63

Здесь мы видим, что будущая стоимость этого аннуитета составит 5 525,63 доллара после того, как все платежи денежного потока будут получены и инвестированы в 5 %.

Заключение по аннуитетному платежу

При расчете заключения по аннуитетному платежу следует иметь в виду следующие моменты, чтобы быстро понять, что это такое, для чего он используется и как его использовать:

Через равный интервал времени, существует серия денежных потоков, которая называется аннуитетом.
Очень важно знать процентную ставку и количество периодов.
Частота осуществления платежей отражает ставку за период и количество периодов.
Переставив PV формулы аннуитета, вы можете определить формулу аннуитета.
Чтобы найти аннуитетный платеж, вы можете использовать PV уравнения аннуитета.

Калькулятор аннуитетных платежей

Вы можете использовать приведенный ниже калькулятор аннуитетных платежей для расчета как текущей, так и будущей стоимости серии аннуитетных платежей.

Калькулятор немедленной ренты | Рассчитайте прогнозируемую выплату

Сколько ежемесячно выплачивается аннуитетная сумма в размере 100 000 долларов США?

Вы можете оценить ежемесячные выплаты аннуитета, если знаете цену аннуитета, фиксированную процентную ставку, частоту ваших выплат — ежемесячно, ежеквартально или ежегодно — и количество лет, в течение которых аннуитет будет приносить вам доход.

Например, 20-летний фиксированный аннуитет с основной суммой в 100 000 долларов и годовым темпом роста 2 процента принесет ежемесячный доход примерно в 505 долларов.

Мы подчеркиваем слово «примерно» в этом примере, потому что эта оценка не принимает во внимание пол получателя ренты или варианты ценообразования, такие как лимиты, спреды и уровни участия.

Все они уникальны для каждого контракта с покупателем аннуитета, и страховая компания учтет их в уравнении при установке вашей ставки. Кроме того, этот расчет точен только в том случае, если ставка аннуитета фиксирована.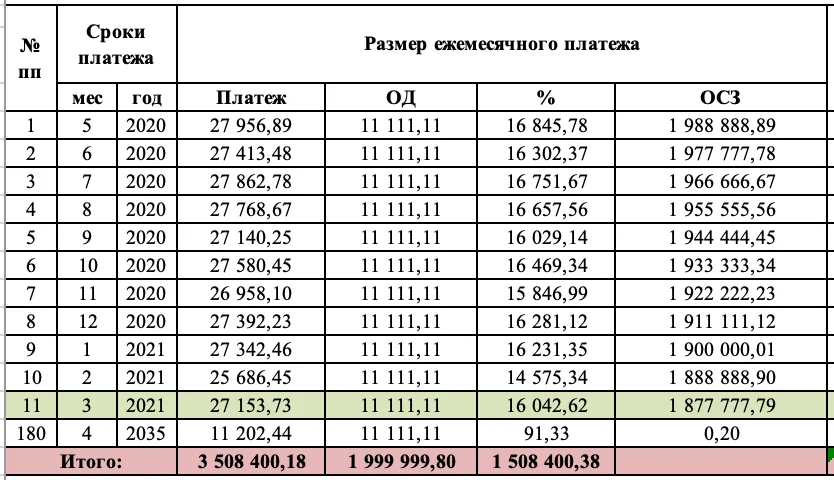 Это не сработает для переменных аннуитетов или других типов аннуитетов с поправкой на рынок или инфляцию.

Как вы рассчитываете аннуитетные выплаты?

Расчет аннуитетных платежей может быть сложной задачей, поскольку страховые компании имеют право устанавливать свои ставки и условия контрактов.

Чтобы получить наилучший результат от калькулятора аннуитета, полезно знать средние ставки аннуитета для того типа аннуитета, который вы планируете купить.

В нашем примере, используя основную сумму 100 000 долларов США при 2-процентной процентной ставке, мы пришли к расчетной сумме ежемесячного платежа, используя формулу, где:

P _O = Основной
PMT = Сумма ежемесячного платежа
r = Годовая процентная ставка
n = Количество платежей в год
t = Количество лет выплат

Используя данные из нашего примера, формула позволяет рассчитать ежемесячные платежи.

Таким образом, при 2-процентном росте ренты в размере 100 000 долларов выплачивается 505,88 долларов в месяц в течение 20 лет.

Помните: этот пример не включает все возможные переменные индивидуальных договоров аннуитета, но твердое понимание этой базовой формулы сделает вас более уверенным в разговоре с финансовым планировщиком или страховым агентом.

Пример MYGA на 500 000 долларов с процентной ставкой 2,85 процента

В случае многолетнего гарантированного аннуитета в размере 500000 долларов США с 2.Процентная ставка 85 процентов, ежемесячные платежи за 10-летний период составят примерно 4 795 долларов.

Поскольку MYGA имеют фиксированные ставки на определенное количество лет, в этом примере мы использовали ту же формулу, но мы подставили разные числа для основной суммы (500 000), процентной ставки (2,85) и количества лет (10).

Опять же, мы не приняли во внимание особенности контракта, такие как пол или количество пассажиров, потому что мы не знаем точно, как страховая компания это взвесит.Однако мы знаем, что женщины обычно получают более низкие выплаты, чем мужчины, потому что женщины имеют более продолжительная продолжительность жизни, и райдеры добавляют к цене аннуитета.

КАК РАССЧИТАТЬ РАССРОЧКИ ПО КРЕДИТУ С ГОДОВЫМИ ФАКТОРАМИ

Почти каждый крупный бизнес занимает деньги. Руководителем группы по займам обычно является казначей. Казначей должен постоянно охранять денежные потоки фирмы, а также понимать и управлять влиянием займов на процентные расходы и прибыль компании.Таким образом, казначеям необходимо глубокое и комплексное понимание влияния различных структур заимствования как на денежные потоки фирмы, так и на ее прибыль. Согласование цикличности равных платежей по кредиту может казаться заблудшим в лабиринте. Давайте посмотрим на практическое управление денежными средствами и прибылью.

НАЛИЧНЫЙ КОРОЛЬ

Допустим, мы занимаем 10 миллионов фунтов стерлингов единовременно, с выплатой ежегодными взносами. Очевидно, что кредитор требует полного погашения взятой в долг 10 млн фунтов стерлингов.Они тоже потребуют процентов.
Допустим, процентная ставка 5% годовых.
Проценты за первый год до погашения — это просто первоначальные 10 млн фунтов стерлингов x 5% = 0,5 млн фунтов стерлингов.
Расходы в отчете о прибылях и убытках, уменьшающие чистую прибыль за первый год, составляют 0,5 млн фунтов стерлингов.
Но следующий год может показаться сложным.

БИЗНЕС-ДИЛЕММА

Наша рассрочка погасит часть основной суммы долга, а также выплатит проценты. Это означает, что проценты за второй год будут меньше, чем за первый год из-за выплаты основной суммы долга.Но что, если в предыдущие годы мы не можем позволить себе более крупную рассрочку? Можем ли мы сделать так, чтобы наши общие денежные потоки были одинаковыми каждый год? Существует ли равный взнос, который будет погашать только правильную сумму основного долга в течение каждого года, чтобы к концу оставить первоначальный заем погашенным вместе со всеми уменьшающимися годовыми процентными сборами?

РЕШИТЕЛЬ КРУГОВ

Помощь всегда под рукой. Действительно, существует равный взнос, который делает именно это, иногда его называют равным взносом. Равные взносы выплачивают различные пропорции процентов и основной суммы в течение каждого периода, так что к концу ссуда была выплачена полностью.
Приравненные платежи хорошо решают нашу проблему с денежными потоками, но проценты по-прежнему кажутся сложными.

Равный взнос
Равный по стоимости взнос по сравнению с другими платежами.
Приравниваемый взнос = основной капитал ÷ коэффициент аннуитета

ДИНАМИЧЕСКИЙ БАЛАНС

Как мы видели, проценты начисляются только с уменьшающегося остатка основной суммы долга. Таким образом, процентная ставка за период вначале относительно велика, а затем становится меньше с каждым ежегодным погашением.

Расчет процентов потенциально сложен, даже цикличен, потому что наши выплаты по основной сумме также меняются. Поскольку процентный элемент
рассрочки уменьшается каждый год, остаток, доступный для выплаты основной суммы долга, каждый раз увеличивается.
Как мы можем вычислить различные годовые процентные ставки? Давайте посмотрим на этот пример:

Строительная компания

Southee Limited планирует приобрести новое землеройное оборудование стоимостью 10 млн фунтов стерлингов.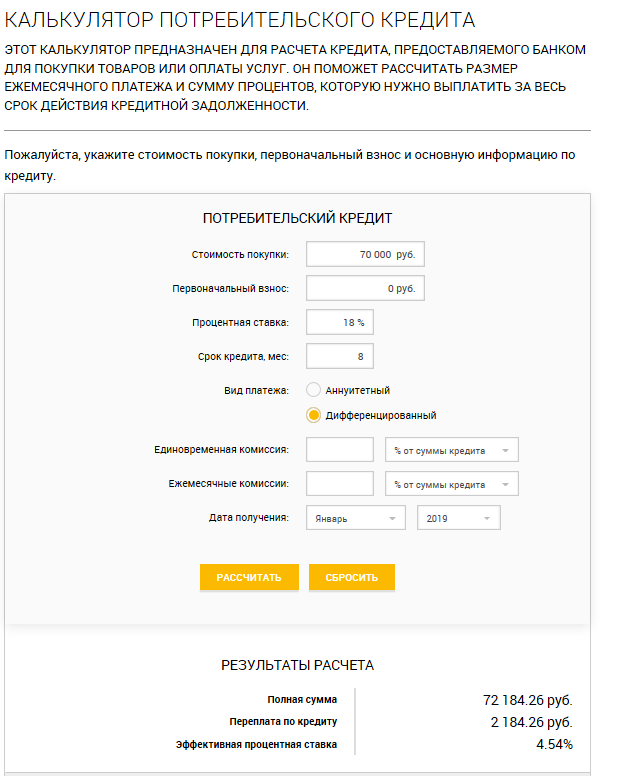 Southee рассматривает возможность получения банковской ссуды на полную стоимость оборудования со сроком погашения в течение четырех лет равными ежегодными платежами, включая проценты по ставке 5% годовых, первый взнос должен быть выплачен через год с даты получения кредита. .

Вы должны быть в состоянии рассчитать годовой взнос, который будет выплачиваться по банковской ссуде, вычислить, какая сумма будет представлять собой выплату основного долга, а также какая сумма будет представлять собой процентные платежи в каждый из четырех лет и в целом.

Другими словами, вам нужно уметь работать над этими пятью вещами:

(1) Ежегодный взнос
(2) Общая сумма выплат по основной сумме
(3) Общая сумма процентов
(4) Выплата процентов за каждый год
(5) Выплаты по основной сумме за каждый год

ГОДОВАЯ РАССРОЧКА

Лучше всего начать с годового взноса.Для расчета годового взноса нам понадобится коэффициент аннуитета. Коэффициент аннуитета (AF) — это отношение нашего приравненного к нему годового взноса к основной сумме в 10 миллионов фунтов стерлингов, взятой в начале.

Сам коэффициент аннуитета рассчитывается как:
AF = (1 — (1 + r) ^-n) ÷ r

Где:
r = процентная ставка за период = 0,05 (5%)
n = количество периодов = 4 (лет)
Применение формулы:
AF = (1 — 1,05 ^-4) ÷ 0,05 = 3,55

Теперь приравненный годовой взнос определяется как:
Рассрочка = основной капитал ÷ коэффициент аннуитета = 10 млн фунтов стерлингов ÷ 3.55 = 2,82 млн фунтов стерлингов

ИТОГО ОСНОВНЫЕ ВЫПЛАТЫ

Общая сумма погашения основной суммы долга — это просто общая сумма первоначально взятой суммы основного долга, то есть 10 миллионов фунтов стерлингов.

ИТОГО ПРОЦЕНТНЫЕ НАПРАВЛЕНИЯ

Общая сумма процентов — это сумма всех выплат за вычетом общей суммы погашения основной суммы долга. Мы выплачиваем только основную сумму долга и проценты, поэтому любая выплаченная сумма, не являющаяся основной суммой, должна быть процентами.

Есть четыре платежа по 2,82 миллиона фунтов каждый.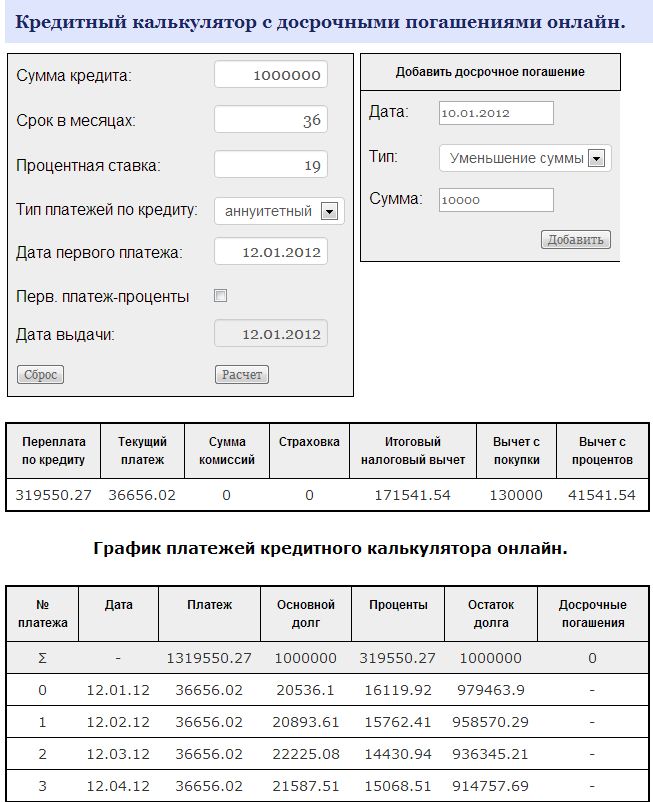

Таким образом, общая сумма выплат составляет: 2 фунта стерлингов.82 м x 4 = 11,3 млн фунтов стерлингов

И общие процентные расходы за четыре года составляют: 11,3 млн фунтов минус 10 млн = 1,3 млн фунтов стерлингов

Теперь нам нужно распределить эти 1,3 миллиона фунтов стерлингов на каждый из четырех лет.

ПРОЦЕНТОВ ЗА КАЖДЫЙ ГОД

Распределения легче вычислить в красивой таблице. Давайте потратим немного времени на один, заполнив уже известные цифры. (Все суммы указаны в млн фунтов стерлингов)

Конечное сальдо каждого года будет начальным сальдо на следующий год.

К тому времени, когда мы подойдем к концу четвертого года, мы выплатим все первоначально взятые 10 миллионов фунтов стерлингов вместе с процентами в размере 1,3 миллиона фунтов стерлингов.

ОСНОВНЫЕ ВЫПЛАТЫ В КАЖДЫЙ ГОД

Теперь мы можем вносить 5% годовых, и все наши цифры будут в порядке.

Мы уже рассчитали процентную ставку за первый год:
0,05 x 10 млн фунтов стерлингов = 0,5 млн фунтов стерлингов

Итак, наше итоговое сальдо за первый год составляет:
Начальное сальдо + проценты — взнос = 10. 00 + 0,5 — 2,82 = 7,68 млн фунтов стерлингов

Итак, мы можем продолжить заполнение остальной части нашей таблицы, как указано ниже:

(Есть небольшая разница в округлении в 0,01 млн фунтов стерлингов за четвертый год, о которой нам не нужно беспокоиться. Она исчезнет, если мы будем использовать больше десятичных знаков.)

____________________

Автор: Дуг Уильямсон

Источник: Журнал Казначей