Определение коэффициента неравномерности распределения
В случае отсутствия ПО «Аттестация вибростендов» все необходимые измерения можно произвести при помощи программного обеспечения ZETLAB.
Определение коэффициента неравномерности распределения проводится в номинальном диапазоне частот при постоянных значениях ускорения и (или) перемещения в контрольной точке не менее 0,3 верхних пределов номинальных диапазонов ускорения и (или) перемещения по результатам измерений ускорения и (или) перемещения при помощи программы «Вольтметр переменного тока».
На рабочей поверхности вибростенда устанавливаются несколько акселерометров (рисунок 1). Далее при помощи программы «Вольтметр переменного тока» оцениваются значения ускорения и (или) перемещения для каждого вибродатчика.
Рисунок 1
Рабочий стол оператора на экране анализатора спектра представлен на рисунке 2. В левой части экрана расположены окна программ «Генератор сигналов различной формы», «Формула», программы «Вольтметр переменного тока» и «Вольтметр постоянного тока». В правой части экрана — программы «Многоканальный осциллограф». Здесь датчик «BC 112 8099» является контрольным и располагается в центре стола, а остальные датчики измерительными и располагаются по краям. Значения с датчиков следует считывать с помощью программы «Вольтметр переменного тока».
Рисунок 2. Рабочий стол анализатора спектра на экране оператора
Рисунок 3. Измерение значения с контрольного датчика «ВС 112 8099»
Рисунок 4. Измерение значения с датчика «ВС 112 8090»
Рисунок 5. Измерение значения с датчика»ВС 112 8024″
Рисунок 6. Измерение значения с датчика»ВС 112 8021«
Коэффициент неравномерности распределения на данном режиме работы виброустановки в процентах определяется по формуле:
где ai — ускорение или перемещение в i-ой точке крепления; ak — ускорение или перемещение в контрольной точке.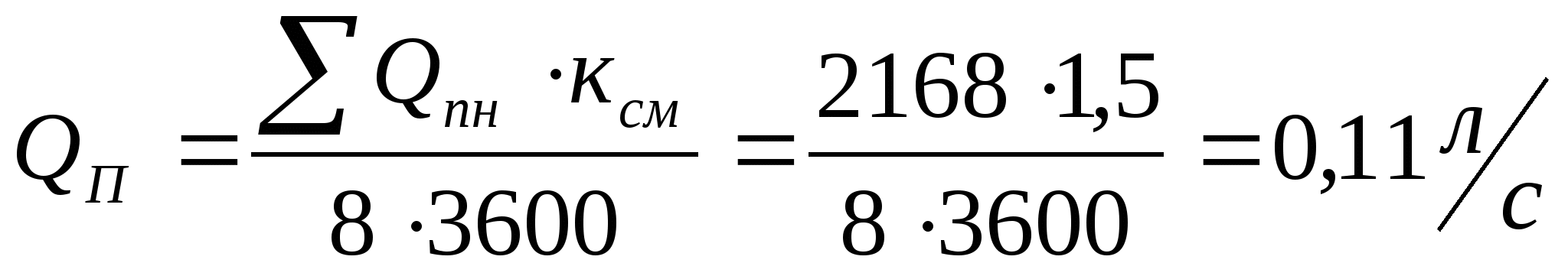
Рисунок 7. Программа «Формула» для автоматического расчета коэффициента неравномерности распределения
Для автоматического расчёта коэффициента неравномерности распределения по четырём датчикам необходимо запустить программу «Формула» и задать шесть формул:
1.Наименование формулы: «Модуль 1»; единицы измерения: «g»; формула: » (StdDev(, 1.0) — StdDev(, 1.0))| «.
3.Наименование формулы: „Модуль 3“; единицы измерения: „g“; формула: » (StdDev(, 1.0) — StdDev(, 1.0))| «.
4.Наименование формулы: „Больше 1“; единицы измерения: „g“; формула: » Greater(<Модуль 1>, <Модуль 2>) * (<Модуль 1> — <Модуль 2>) + <Модуль 2> «.
5.Наименование формулы: „Больше 2“; единицы измерения: „g“; формула: » Greater(<Больше 1>, <Модуль 3>) * (<Больше 1> — <Модуль 3>) + <Модуль 3> «.
6.Наименование формулы: „Коэффициент“; единицы измерения: „%“; формула: » <Больше 2> / StdDev(, 1.0) * 100 «.
Значения каналов программы «Формула» следует смотреть в программе «Вольтметр постоянного тока».
Рисунок 8. Измерение значения формулы»Модуль 1«
Рисунок 9. Измерение значения формулы «Модуль 2»
Рисунок 10.Измерение значения формулы «Модуль 3»
Рисунок 11. Измерение значения формулы «Больше 1»
Рисунок 12. Измерение значения формулы «Больше 2»
Рисунок 13. Измерение значения формулы «Коэффициент»
Используя программу «Многоканальный самописец», можно проследить за изменением ускорения в различных точках вибростола в течение длительного промежутка времени (рисунок 14).
Рисунок 14. Программа «Многоканальный самописец» для наблюдения изменения ускорения
См. также:
Коэффициент неравномерности подачи — Справочник химика 21
Неравномерность подачи насоса оценивается коэффициентом неравномерности подачи, который пр дста(вля т собой колебание подачи в долях средней подачи [c.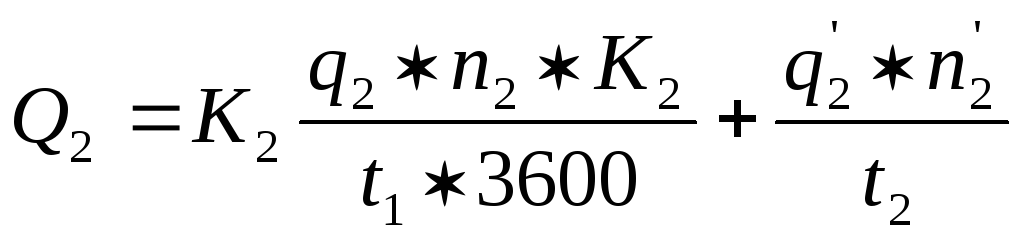 206]
206] Преимуществами зубчатых насосов являются отсутствие клапанов, легкость, компактность, реверсивность, непосредственное соединение с электродвигателем и сравнительно низкий коэффициент неравномерности подачи. К недостаткам Этих насосов относятся низкий коэффициент полезного действия (Лн 0>6—0,7), Небольшая производительность и высокие требования к чистоте перекачиваемой жидкости.
Неравномерность подачи жидкости насосом оценивают коэффициентом неравномерности подачи, представляющим собой отношение максимальной подачи жидкости за один рабочий цикл к среднему значению подачи д р. [c.112]
При гидравлическом расчете рассолопроводов принимаются плотность рассола — 1,2 г/см вязкость — 1,05—1,1 сП коэффициенты местного сопротивления трубопровода — 1,05—1,15 по сравнению с водой коэффициент неравномерности подачи рассола, связанный с восстановлением аварийного запаса и неравномерной работой потребителя,— 1,1—1,2.
Заметим, что влияние инерционного напора на величины гв1 Put в и Лн, значительное для насоса простого действия, сильно ослабляется по мере уменьшения коэффициента неравномерности подачи (увеличения кратности действия). [c.114]
Пренебрегая плош,адью штока, можно вычислить коэффициент неравномерности подачи такого насоса. Если иметь в виду, что (оо=я/ /г/30, то используя выражения (6.7) и (6.10), получаем а=я/2. [c.231]
Рабочую емкость камеры реакции подсчитывают умножением средней интенсивности подачи сточных вод на установленную продолжительность цикла. Подсчитанная таким образом рабочая емкость реакционной камеры соответствует лишь условиям средней подачи сточных вод, поэтому необходимо ее увеличить на значение коэффициента неравномерности подачи сточных вод за цикл. Этот коэффициент равен отношению максимального количества сточных вод, подаваемых за один цикл, к среднему значению.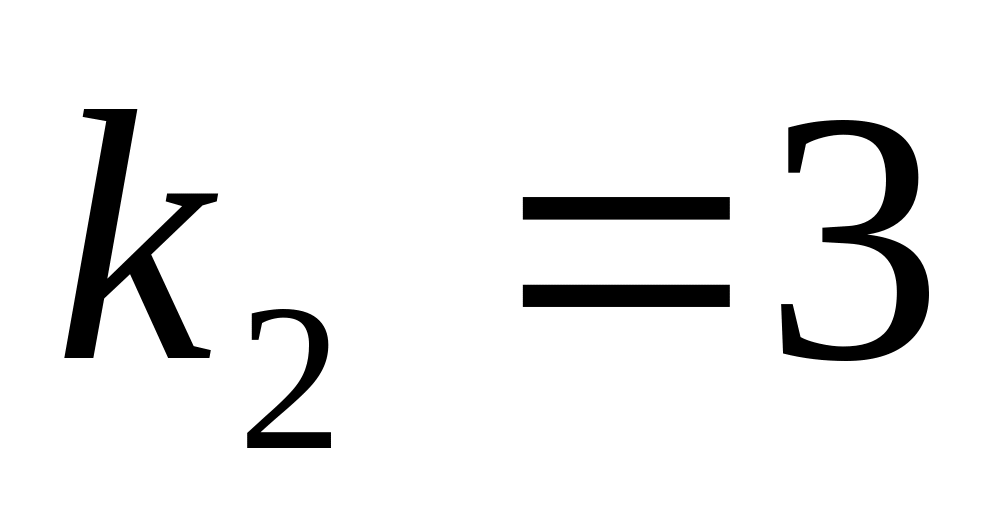
Поэтому при коэффициенте неравномерности подачи —, [c.203]
У четырехплунжерного насоса нодача менее равномерна, чем у трехплунжерного. Здесь коэффициент неравномерности подачи а = 0,342. У пятиплунжерного насоса коэффициент неравномерности подачи равен всего 0,05.
Если при работе насоса подача его колеблется от Qмш до Смаке, то неравномерность подачи характеризуют величиной коэффициента неравномерности подачи [c.277]
П — число подач вагонов в сутки принимаем Я = 4 гПп.в — коэффициент неравномерности подачи вагонов принимаем т ,е 1,25. [c.21]
Коэффициент неравномерности подачи, обусловленный пуль- [c.119]
Это выражение справедливо для положительного значения sin 7. Из сравнения его с выражением (49) следует, что коэффициент неравномерности подачи гидромашины с плоской напра-вляющей меньше коэффициента гидромашины с цилиндрической направляющей, особенно при больших подачах.
Большинству типов роторных насосов свойственна неравномерность подачи. Если при работе насоса подача его колеблется от (Эмин до Сманс, то неравномерность подачи характеризуют коэффициентом неравномерности подачи [c.289]
Соединив гри одноплунжерных насоса, получим трехплунжерный асос. Кривошипы трехплунжерного насоса располагаются под углами 120° друг к другу. Из рис. 12-4 видно, что диаграммы подач разных цилиндров частично перекрывают друг друга, т. е. в некоторые моменты имеет место одноеременная подача двумя цилиндрами. Для получения окончательного графика подачи надо сложить одновременно подаваемые мгновенные расходы. Получаем диаграмму подачи, изображенную на рис. 13-4 толстой линией. У трехплунжерного насоса коэффициент неравномерности подачи 0 = 0,141.
Минимальная мгновенная подача QJ = = 0. Коэффициент неравномерности подачи Р8пп [c.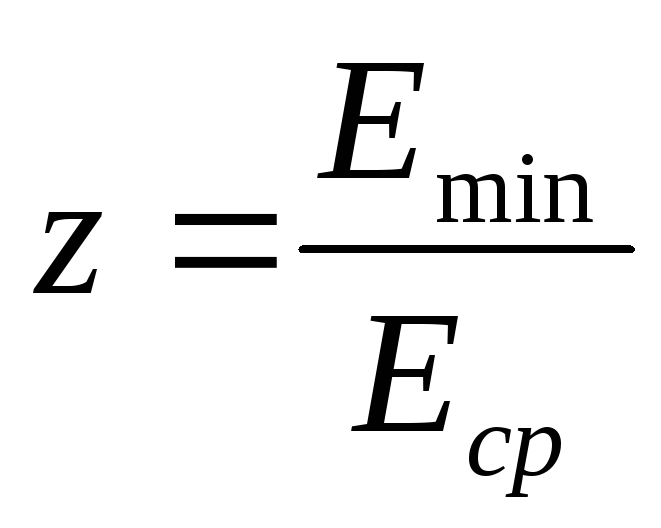 207]
207]
Если при работе пасоса подача е10 колеблепся от Смиа до Рмакс, то неравномерность подачи характери.зуют величиной коэффициента неравномерности подачи [c.274]
Коэффициент неравномерности потребления воды — Энциклопедия по машиностроению XXL
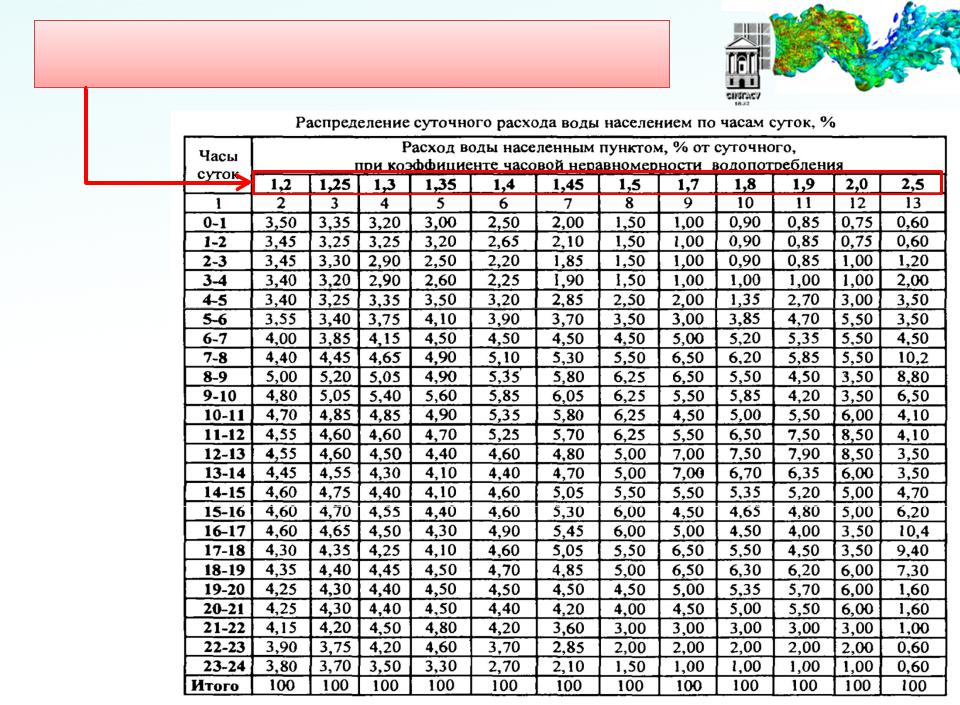
Зная среднесуточный расход воды и коэффициенты неравномерности потребления, можно рассчитать максимальный часовой расходКоэффициент часовой неравномерности водопотребления для населенных пунктов принимают в зависимости от нормы водопотребления. Коэффициент часовой неравномерности хозяйственно-питьевого водопотребления на промышленных предприятиях принимают равным 2,5 или 3 (см. табл. П.2). Коэффициент часовой неравномерности потребления воды для производственных нужд может быть различным и зависит от технологии. [c.86]
На промышленных предприятиях коэффициент суточной неравномерности хозяйственно-питьевого водопотребления принимают равным единице, т. е. считают, что водопотребление равномерно в течение года. Неравномерность потребления производственной воды зависит от принятой технологии, количества вырабатываемой продукции, а для некоторых производств — от времени года. Последнее относится прежде всего к производствам, расходующим воду на
Пример 9.8. Определить емкость водонапорного бака при хозяйственном расходе воды 20 л/с и 10%-ной неравномерности от суточного потребления воды. Расход на внутреннее пожаротушение составляет 7 л/с коэффициент неравномерности— 1,3. [c.169]
Кобщ—общий коэффициент неравномерности потребления воды на производственные нужды, равный 1,46—il,7. [c.478]
Кобщ — общий коэффициент неравномерности потребления воды в рабочих поселках, рааный 1,7—2,2. [c.478]
Потребление воды населением в течение года неравномерно. Так, летом ее расходуют больше, чем зимой, в предвыходные дни больше, чем в остальные дни недели. Отношение суточного расхода в дни наибольшего водопотребления Q ax yT среднему суточному расходу Q P.tyT называют коэффициентом суточной неравномерности водопотребления-.
[c.85]
Так, летом ее расходуют больше, чем зимой, в предвыходные дни больше, чем в остальные дни недели. Отношение суточного расхода в дни наибольшего водопотребления Q ax yT среднему суточному расходу Q P.tyT называют коэффициентом суточной неравномерности водопотребления-.
[c.85]
Коэффициент неравномерности — Энциклопедия по машиностроению XXL
Колебание угловой скорости звена приведения при установившемся движении оценивается либо коэффициентом неравномерности движения, имеющим I ид [c.159]Интервал Aq>, в течение которого скорость (О изменялась от наименьшего до наибольшего значений, равен п, поэтому динамический коэффициент неравномерности движения Артоболевского будет равен [c.166]
Определить, какой должна быть величина момента инерции маховика, устанавливаемого на валу А звена АВ, чтобы коэффициент неравномерности движения б был равен 0,08. [c.171]
Определить величину махового момента т Dh маховика, устанавливаемого на валу А звена АВ, при которой коэффициент неравномерности движения б будет равен 0,02. [c.173]
Найти величину момента инерции / маховика, при котором буд(. т обеспечен коэффициент неравномерности движения б = 0,25. [c.175]
Средняя скорость машины и ее коэффициент неравномерности движения [c.375]
Fi таблице 5 приводятся допустимые коэффициенты неравномерности хода для некоторых типов машин. Удобно среднюю скорость механизма или машины и коэффициент неравномерности движения выражать через углы поворота [c.376]
Из построения непосредственно следует, что чем меньше коэффициент неравномерности б, тем меньше разница между углами и н тем дальше, очевидно, от участка кривой Т = Т J ), [c.380]
Чтобы повысить тепловыделение в периферийной области активной зоны, необходимо использовать разное обогащение ядерного топлива. При этом по мере удаления от центра активной зоны обогащение свежих твэлов должно увеличиваться. Простейшим случаем является образование двух зон с разным обогащением. Размеры зон и обогащение в них выбираются из условия получения минимального коэффициента неравномерности Кг-
[c.21]
При этом по мере удаления от центра активной зоны обогащение свежих твэлов должно увеличиваться. Простейшим случаем является образование двух зон с разным обогащением. Размеры зон и обогащение в них выбираются из условия получения минимального коэффициента неравномерности Кг-
[c.21]
Объемный коэффициент неравномерно- 3,51 сти тепловыделения [c.22]
Коэффициент неравномерности теплоотдачи по поверхности шаров составляет 2,2—4,0 в зависимости от значения N, что практически совпадает с данными исследований из работ [41 и 42] и исследований В. К. Ламба и автора настоящей работы. [c.86]
И2/ д J 4) коэффициент неравномерности вращения кривошипа 6 = 0,01 5) расчетный модуль зубчатых колес т = 2 мм. [c.202]
Коэффициент неравномерности вращения кривошипа б [c.204]
Отношение выступа шатуна к радиусу кривошипа r jr Коэффициент неравномерности вращения кривошипа б [c.207]
Силы и массы машинного агрегата приведены к звену АВ. Движущий момент в течение трех первых (от начала движения) оборотов звена Л В меняется по закону прямой аЬ, а далее по периодическому закону, соответствуюш,ему ломаной линии bed. Момент сопротивления подключается в конце третьего оборота, считая от начала движения, и равен = 230 нм, оставаясь все время постоянным. Приведенный момент инерции постоянен и равен / 0,2кем . Выяснить, возможно ли установившееся движение звена АВ, и если возможно, то определить коэффициент неравномерности б этого движения. [c.155]
В установившемся движении машинного агрегата его диаграмма Виттенбауэра представляет собой отрезок прямой тп, параллельный оси Т диаграммы. Длина отрезка тп равна 50 мм. Коорди-иать точки т равны Хт = 50 мм, = ЮО мм. Определить коэффициент неравномерности движения установившегося режима, если масштабы по осям координат диаграммы Виттенбауэра равны Иг == 10 hmImm, = 1,0 кгм /мм.
 [c.155]
[c.155]С)пределить коэффициент неравномерности установившегося движения, если масштабы по осям координат диаграммы Виттенбауэра равны цт- = 20 hmImm, = 0,5 кг/мм. [c.155]
Если разность максимального и минимального значений скорости Уд точки В (рис. 19.1) разделить на среднюю скорость, ю получим так называемый коэффициент неравномерности deuoi -ния механизма или машины, обозначаемый через б н равный [c.376]
Коэффициент неравномерности движения характеризует только перепад угловой скорости начального звена в пределах от п до сошах, но не характеризует динамики двилсения этого звена [c.377]
Если принять (Оср = ( max + mln)/2, ТО, рСШЭЯ СОВМесТИО уравнения (19.5), (19.6) и (19.9), получаем, что коэффициент неравномерности хода б механизма равен [c.379]
Определить коэффициент неравномерности движения S мехн-низма можно и непосредственно, если построена диаграмма скоростей (например, по диаграмме скоростей, построенной на рис. 19.1). Для этого определяем у, ах и Umm по диаграмме и подставляем их значения в формулы (19.2) и (19.3). [c.379]
С помощью формул (19.16) можно для заданной угловой скорости Иср и для любого заданного значения коэффициента неравномерности движения б определить соответствующие углы 3тах [c.380]
Далее, при решении задачи о ма.ч овике задаются желательным для машикъ коэффициентом неравномерности движения (см. формулу (19.10)). Имея заданными и 6, можно определить по формулам (19.14) максимальную (й, ах и минимальную [c.384]
Если построить зависимость между моментом инерции маховика и коэффициентом неравномерности движения б, то можно обнаружить, что эта зависимость имеет приближенно гиперболический характер (рис, 19.11). Таким обра 1М, с приближением б к нулю момент инерции маховика быстро возрастает, и, следовательно, для незначительного умешзшения б в этой области необходимо значительное увеличение момента инерции махе-
[c. 392]
392]
На рис. 1.4 показано распределение тепловыделения по радиусу активной зоны, пронормироаанного к среднему значению, равному 1, для двух вариантов двухзонного профилирования. Как видно из рисунков, коэффициент неравномерности во втором варианте больше, чем в первом, что объясняется слишком большой разницей в обогащении топлива. Глубина выгорания в центральной зоне увеличивается, а в периферийной — [c.21]
Полученные выражения согласуются с критериальным уравнением (6-3). В отличие от последнего зависимости (6-7) и (6-8 ) непосредственно указывают (с учетом исходных допущений) по крайней мере на три важнейших обстоятельства 1) интенсивность теплообмена с потоком газовзвеси выше, чем с чисто газовым потоком 2) относительное приращение интенсивности ANun/Nu прямо пропорционально отношению коэффициентов аэродинамического трения т/ и отношению коэффициентов неравномерности (скольжения) компонентов по скорости и температуре если в общем случае то ANun/Nu пропорционально концентрации твердого компонента в степени л 1 3) относительное приращение интенсивности теплообмена прямо пропорционально отношению теплоемкостей компонентов Ст/с. [c.185]
Как рассчитать освещенность помещения – коэффициент неравномерности освещения
Правильно организованное освещение производственных помещений весьма благотворно отражается на работоспособности персонала и его здоровье. Недостаток света, наоборот, приводит к утомляемости и раздражительности человека. Кроме того, при длительном нахождении в плохого расчёта освещения в помещении от чрезмерного напряжения глаз падает уровень остроты зрения. Слишком яркий свет может привести к фотоожогам глаз, перевозбуждению нервной системы и прочим неприятностям. Поэтому вопрос рационального освещения рабочей зоны настолько важен, что для его нормирования разработаны санитарные и строительные нормативы. Соблюдение их требований обязательны для проектировщиков и руководителей предприятий.
Соблюдение их требований обязательны для проектировщиков и руководителей предприятий.
Правильное освещение производственного помещения
По видам производственное освещение помещения (как и любого другого) делится на естественное и искусственное. Естественный свет – наиболее ценен: человеческий глаз максимально к нему приспособлен. Он поступает внутрь здания через окна и прочие прозрачные строительные конструкции (например, аэрационные фонари).
Виды искусственного освещения: общим; местным; комбинированным. Местное освещение само по себе не используется, его применяют только в комбинации с общим. Подходящий для этого осветительный прибор может быть переносным или стационарным. Световое пятно от него не освещает даже прилегающие к нему площади.
Комбинированный метод освещенности здания
Комбинированное – требуется при выполнении рабочим высокоточных операций, не допускающих возникновения резких теней от каких-либо предметов.
Общее – организуется в цехах с однотипными работами (например, в литейных). Встречаются случаи, когда комбинированное освещение просто нет возможности организовать. Установленная освещенность для рабочих мест с мелкими работами соответствует 500-м Лк, постепенно снижаясь до 50 Лк в различных хранилищах. Для максимальной экономичности, можно осветить технические или уличные территории приборами с датчиками движения для включения света.
Общая методика расчета
Расчетом параметров осветительной системы занимается инженер-электрик (проектировщик). Он может выполнить эту работу одним из трех способов:
- через коэффициент использования потока света;
- установки удельной мощности;
- точечным.
Первым способом рассчитывается общее (равномерное) освещение рабочих поверхностей, расположенных в горизонтальной плоскости. В процессе работы вычисляется коэффициент для отдельно взятого помещения. В методике учитываются геометрические размеры производственного участка и степень светового отражения поверхностей.
Расчет через удельную мощность. Способ светотехнического расчета через удельную мощность используется только для предварительной прикидки установленной мощности осветительных установок, так как дает весьма приближенный результат. Такие данные часто требуются для заполнения опросных листов, которые используются при получении технических условий или при составлении сметной стоимости монтажа осветительной системы предприятия. Точечный метод. Такой способ пригоден для расчета освещения – локализованного и общего – при наличии осветительных приборах прямого света. На него не влияет пространственная ориентация анализируемой поверхности. Освещенность подсчитывают в каждой точке поверхности для каждого источника света в отдельности.
Реализация точечного метода представляет собой очень трудоемкий процесс, но и точность результата высокая. Правда, она зависит от добросовестности специалиста, выполняющего анализ.
Как рассчитать алгоритм
Расчет освещения участков производственных предприятий производится в следующей последовательности:
- выбирается система освещения;
- обосновывается нормированная освещенность каждого рабочего места;
- выбирается наиболее рациональный и экономичный светильник;
- оцениваются коэффициенты неравномерности освещения, запаса освещенности, отражения поверхностей, находящихся внутри помещения.
После этого рассчитываются: индекс помещения; коэффициент использования светового потока; необходимое количество светильников; На заключительном этапе выполняется чертеж или эскиз, на котором размечается расположение всех светильников.
Как рассчитывается норма КЕО
Естественный свет – величина непостоянная, потому и нормируется он не по освещенности, а по ее коэффициенту (КЕО). Он рассчитывается по формуле:
Е = (Ев/Ен) х 100, %, где:
Ев – естественная освещенность точки, расположенной внутри помещения;
Ен – наружная освещенность (горизонтальная) при небосводе, открытом полностью.
Очередность шагов
Первым делом выбирается система освещения. Оно может быть боковым, верхним или комбинированным. Выбор зависит от назначения производственного помещения с обязательным учетом особенностей технологического процесса.
Нормированное значение КЕО выбирается по таблице СНиП 23-05-95. Его величина зависит от разряда зрительной работы (а разряд определяется в зависимости от величины самого мелкого элемента, с которым приходится работать рабочему).
Величина Ен корректируется в зависимости от района расположения производственного объекта.
КЕО снижается из-за запыленности поверхностей, пропускающих свет. Для учета степени загрязненности остекления выбирается коэффициент запаса Кз.
Световая характеристика проемов определяется в соответствии с:
- соотношением длины и глубины помещения, глубины и высоты (от уровня рабочей поверхности до верхней границы окна) – при боковом освещении;
- соотношением длины и ширины помещения, его высоты и ширины и типа фонаря – при верхнем освещении.
При боковом освещении нормируется КЕО (его минимальное значение) для рабочего места, наиболее удаленного от окна. При верхнем или комбинированном – нормированный показатель является средним для пяти точек, равноудаленных друг от друга и расположенных на рабочей поверхности. Целью расчета естественного освещения является определение площади оконных проемов. Если рабочее место расположено менее чем в двенадцати метрах от окна, достаточно одностороннего освещения. При увеличении расстояния свыше 12 метров необходимо обеспечить рабочую точку двухсторонним боковым освещением.
Естественный свет
Имеется помещение длиной L = 10 м, шириной B – 10 м, высотой H -5 м. оконный проем имеет размеры 4х3,5 м с двойным остеклением.
По условиям задачи помещение расположено в третьем световом поясе. Точность зрительной работы персонала – высокая.
Нормированное значение КПО – 2%.
Окна ориентированы на север, они обеспечивают КЕО не менее 1,5%.
Для обеспечения КПО 2% необходимо наличие в помещении трех окон общей площадью 42 кв.м.
Искусственный свет
Дано помещение с геометрическими размерами 8х6х3,5 м.
Нормируемая освещенность для данного производства – 300 лк.
Напряжение в сети предприятия – 220 В, предполагается использовать светильники люминесцентные ЛПО (коэффициент использования светового потока – 49%).
Отражательная способность:
- потолка -0,7;
- стен – 0,5;
- рабочей поверхности – 0,3.
Коэффициенты:
- запаса Кз = 1,75;
- неравномерности освещения – 1,1.
Разряд зрительных работ, выполняемых персоналом в данном помещении – III.
Рабочая поверхность КРЛ размещена на высоте 0,8 м, высота свеса – 0,1 м.
Площадь участка составляет 48 кв. м. Индекс помещения (S/(h2 – h3) (L+B) = 48/(3,5 – 0,8) (8 + 6) = 1,26
Коэффициент использования (в соответствии с коэф. отражения поверхностями и индексом помещения) составляет 51. Количество светильников N = (500 х 48 х 100х1,75)/(51 х 4 х 1150) = 17,9 Округлив результат, получим необходимое количество светильников, равное 18 шт.
Расположение осветительных приборов и их количество
Светильники могут размещаться с учетом, либо без учета размещения рабочих мест.
Если выбирается за основу система равномерного освещения цеха, они располагаются высоко от рабочих поверхностей, могут оснащаться дополнительными отражателями.
Поток света иногда направляется не только вниз, но и вверх или в стороны.
При организации комбинированного освещения местные светильники устанавливаются на каждом рабочем месте. Световой поток от местного осветительного прибора не должен попадать в поле зрения работающего. В качестве источника света в производственных помещениях могут использоваться лампы различных типов: люминесцентные (наиболее часто применяемые), газоразрядные, накаливания.
Коэффициент KHbeta — Micro Express
По мере проворота зубчатых колёс в паре под нагрузкой точка контакта смещается по рабочей поверхности зуба. В идеальном случае (т.е. при абсолютно правильной геометрии и абсолютно жестких материалах колёс) напряжения, возникающие в точке контакта должны быть постоянны. Но на практике это далеко не так, и непостоянность возникающих напряжений в расчёте на прочность принято учитывать спрециальным коэффициентом – коэффициентом неравномерности распределения нагрузки по длине контактных линий KHβ.
Причинами неравномерного распределения нагрузки по длине контактных линий являются многие факторы: эквивалентная погрешность зубчатого зацепления в плоскости контакта зубчатых колес, упругие деформации зубчатых колес, упругие деформации корпусных деталей и валов, смещения опорных поверхностей валов из-за упругих деформаций подшипников, технологические отклонения и температурные деформации и так далее. Совместное действие таких факторов, как технологические отклонения корпуса и зубчатых колес, изгиб корпуса, смещение обойм радиально-упорных подшипников приводит к практически линейным отклонениям от теоретической плоскости зацепления. В тоже время упругие деформации зубчатых колес, корпуса и температурные деформации приводят к нелинейному отклонению в плоскости зацепления. В дополнение к этому на точность зацепления оказывают влияние неровности поверхности и отклонение формы зуба самих зубчатых колёс. Таким образом, неравномерность распределения нагрузки может быть выше расчётных допущений даже не смотря на фактор приработки контактирующих зубчатых колес после первоначальной обкатки изделия.
Различие расчётных методик при оценке коэффициента неравномерности распределения нагрузки по длине контактных линийПараметр коэффициента неравномерности KHβ по ГОСТ определяется по графику от отношения ширины колеса к диаметру, и компоновочной схемы зубчатого колеса.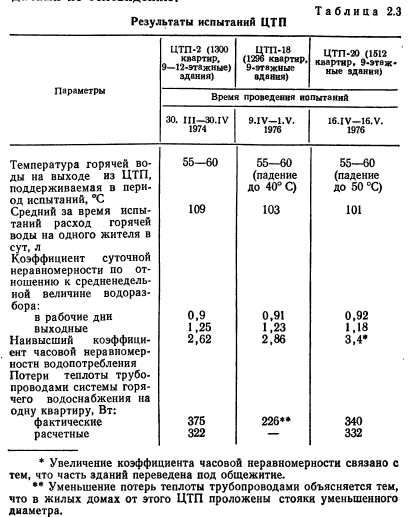
Параметр коэффициента KHβ по ISO – расчётная величина, зависящая от велечины деформации валов в местах установки зубчатых колес под нагрузкой, а также точности позиционирования и изготовления зубчатого колеса. Понятно, что чем выше KHβ, тем хуже качество зацепления. При расчете с учетом спектра нагружения, коэффициенты KHβ должны быть определены для каждой ступени нагружения индивидуально.
Далее мы приводим пример сравнения значений коэффициента KHβ для определённой зубчатой пары, рассчитаный и найденный по методике ГОСТ и ISO табличном и графическом виде:
синим – значения KHβ по методике ГОСТ
черным – значения KHβ по методике ISO при неоптимизированном пятне контакта
красным – значения KHβ по методике ISO при оптимизированном пятне контакта
На основании приведенных выше результатов расчета коэффициента KHβ (в модуле анализа пятна контакта KISSsoft), изображенных на картинке, следует что в данном примере KHβ = 1,46; Согласно рекомендациям ГОСТ 21354-87 специалист по расчетам должен был бы принять KHβ = 1,05 и эта неточность могла бы быть выявлена только в результате проведения определенного количества натурных испытаний.
Таким образом, из приведённых выше данных видно, что применение таблиц и графиков по ГОСТ может быть оправданно только при приблизительных расчётах зубчатых колес к которым не предъявляются особых требований по надежности. Если же речь идет о серийном производстве, необходимо иметь окончательные, максимально правдивые показатели, что требует учета большего количества исходных параметров. Для того, чтобы выполнить такой расчёт, необходимо мощная расчётная программа со встроенным конечноэлементным решателем, необходимым для точного определения параметров пятна контакта под нагрузкой. Лучшим решением для инженера в отрасли уже более 20 лет является програмный комплекс KissSoft/KissSys.
Лучшим решением для инженера в отрасли уже более 20 лет является програмный комплекс KissSoft/KissSys.
Наш опыт в проектировании отдельных элементов трансмиссии позволяет на стадии прочностного расчета задатся определенным значением коэффициента KHβ, которое будет достигнуто в процессе оптимизации пятна контакта зубчатых зацеплений. Например, при проектировании колесного редуктора трансмиссии карьерного самосвала грузоподъемностью 60тонн, на стадии оптимизации макрогеометрии планетарного ряда, после анализа исходных данных и проведения верификации исходной конструкции коэффициента KHβ был принят не хуже значения в 1,25 для критичных с точки зрения накопления усталостных повреждений ступеней нагружения. В результате оптимизации микрогеометрии планетарной передачи, были достигнуты значения KHβ намного лучшие по сравнению с целевым (1,25) во всем возможном диапазоне опасных режимов работы.
На графике ниже представленны полученные значения коэффициента неравномерности распределения нагрузки KHβ: по оси Х – момент на солнечной шестерне, Нм; по оси Y – Коэффициент KHbeta для пары солнечная шестерня-сателлит (красная линия), Коэффициент KHbeta для пары сателлит-коронная шестерня (синяя линия). При этом максимальное значение момента для самой тяжелонагруженной ступени нагружения из эксперементально измеренного и принятого в расчетах спектра нагружения – составляет 21000 Нм.
Таким образом, оптимизация как параметров макрогеометрии, так и параметров микрогеометрии зубчатых передач с учетом особенностей техпроцесса Вашего предприятия, позволяет обеспечить как теребуемую долговечность, так и необходимый запас прочности во всем диапазоне рабочих нагрузок и требуемые тактико-технические характеристики конечного изделия.
Scroll5. Неравномерность грузовых перевозок
Формулы для решения задач
1. Коэффициент
неравномерности перевозок грузов по
времени:
Коэффициент
неравномерности перевозок грузов по
времени:
а) для месяца пикового объема работы:
,
где – максимальный месячный объем перевозок грузов в году, т;
– среднемесячный объем перевозок грузов за год, т;
– общий объем перевозок за год, т;
б) для каждого месяца (индекс сезонности):
,
где –объем перевозок грузов в i-ом месяце, т;
в) максимальная внутригодовая неравномерность:
,
где – минимальный месячный объем перевозок грузов в году, т.
2. Коэффициент неравномерности перевозок грузов по направлению (коэффициент обратности):
,
при этом всегда ,
где – объем перевозок грузов в груженом направлении, т;
– объем перевозок грузов в порожнем направлении, т.
Задачи
5.1. В таблице приведена густота перевозок в млн. т. одного из грузов на участке. Определить коэффициент неравномерности перевозок данного груза.
№ ц/в | Месяц | Варианты | |||||
1 | 2 | 3 | 4 | 5 | 6 | ||
(1) | Январь | 40 | 60 | 58 | 50 | 45 | 45 |
(2) | Февраль | 35 | 55 | 54 | 48 | 40 | 40 |
(3) | Март | 30 | 50 | 60 | 52 | 47 | 45 |
(3) | Апрель | 41 | 60 | 61 | 56 | 50 | 50 |
(1) | Май | 43 | 70 | 72 | 58 | 53 | 51 |
(2) | Июнь | 50 | 73 | 75 | 60 | 56 | 53 |
(3) | Июль | 52 | 78 | 68 | 65 | 61 | 58 |
(3) | Август | 58 | 80 | 75 | 70 | 68 | 65 |
(1) | Сентябрь | 65 | 85 | 70 | 73 | 70 | 68 |
(2) | Октябрь | 55 | 70 | 68 | 64 | 68 | 72 |
(3) | Ноябрь | 40 | 68 | 50 | 60 | 64 | 70 |
(3) | Декабрь | 30 | 50 | 53 | 58 | 60 | 62 |
5. 2. Определить
неравномерность перевозок грузов во
времени и по направлению, если на участке
железной дороги был зафиксирован объем
перевозок, приведенный в таблице.
2. Определить
неравномерность перевозок грузов во
времени и по направлению, если на участке
железной дороги был зафиксирован объем
перевозок, приведенный в таблице.
№ ц/в | Показатель | Варианты | |||||
1 | 2 | 3 | 4 | 5 | 6 | ||
(1) | Перевозка в 1 квартале, млн. т. | 220 | 180 | 160 | 250 | 230 | 270 |
— в том числе в порожнем направлении | 95 | 75 | 60 | 120 | 75 | 110 | |
(2) | Перевозка
во 2 квартале, млн. | 300 | 310 | 330 | 290 | 280 | 320 |
— в том числе в порожнем направлении | 100 | 130 | 140 | 120 | 110 | 150 | |
(2) | Перевозка в 3 квартале, млн. т. | 270 | 240 | 250 | 260 | 280 | 290 |
— в том числе в порожнем направлении | 85 | 105 | 115 | 110 | 100 | 90 | |
(3) | Перевозка
в 4 квартале, млн. | 150 | 210 | 180 | 220 | 200 | 170 |
— в том числе в порожнем направлении | 70 | 85 | 60 | 90 | 65 | 75 | |
5.3. Определить, сколько дополнительных вагонов и локомотивов необходимо иметь на дороге в резерве для выполнения перевозок в напряженный период работы.
№ ц/в | Показатель | Вариант | |||||
1 | 2 | 3 | 4 | 5 | 6 | ||
(1) | Объем перевозок грузов, млн. т. в год | 55 | 70 | 75 | 85 | 50 | 65 |
(2) | Средняя дальность перевозки грузов, км | 800 | 900 | 600 | 700 | 1000 | 950 |
(3) | Производительность вагона, ткм/сутки | 9000 | 8500 | 9500 | 10000 | 12000 | 9000 |
(3) | Производительность
локомотива, млн. | 1,8 | 1,75 | 1,7 | 1,55 | 1,65 | 1,85 |
(1) | Коэффициент нерабочего парка вагонов и локомотивов, % | 1,25 | 1,20 | 1,15 | 1,22 | 1,16 | 1,18 |
(2) | Соотношение ткм брутто и нетто (коэффициент брутто) | 1,7 | 1,45 | 1,55 | 1,35 | 1,8 | 1,75 |
(3) | Коэффициент неравномерности грузовых перевозок для месяца пикового объема работы | 1,2 | 1,25 | 1,3 | 1,35 | 1,45 | 1,15 |
5. 4. Проанализировать
влияние неравномерности перевозок
грузов по направлениям на показатели
работы вагонного и локомотивного парка
(средний вес поезда брутто, динамическую
нагрузку рабочего вагона, число одиночно
следующих локомотивов в порожнем
направлении) при уменьшении густоты
перевозок в порожнем направлении на
участке. Вагонопотоки по направлениям
одинаковы.
4. Проанализировать
влияние неравномерности перевозок
грузов по направлениям на показатели
работы вагонного и локомотивного парка
(средний вес поезда брутто, динамическую
нагрузку рабочего вагона, число одиночно
следующих локомотивов в порожнем
направлении) при уменьшении густоты
перевозок в порожнем направлении на
участке. Вагонопотоки по направлениям
одинаковы.
№ ц/в | Показатель | Варианты | |||||
1 | 2 | 3 | 4 | 5 | 6 | ||
(1) | Длина участка, км | 800 | 600 | 750 | 820 | 680 | 500 |
(3) | Грузонапряженность участка в млн. ткм/км: в груженом направлении | 45 | 40 | 60 | 55 | 70 | 65 |
в порожнем направлении: до изменения после изменения | 30 20 | 32 25 | 45 35 | 43 40 | 55 40 | 50 35 | |
(3) | Вес груженого поезда брутто, т | 3200 | 3000 | 4000 | 3500 | 4000 | 3800 |
(3) | Состав порожнего поезда, вагонов | 80 | 90 | 100 | 85 | 110 | 70 |
(2) | Вес тары вагона, | 23 | 22 | 21 | 24 | 25 | 20 |
(1) | Динамическая нагрузка груженого вагона, т/вагон | 48 | 40 | 50 | 53 | 45 | 55 |
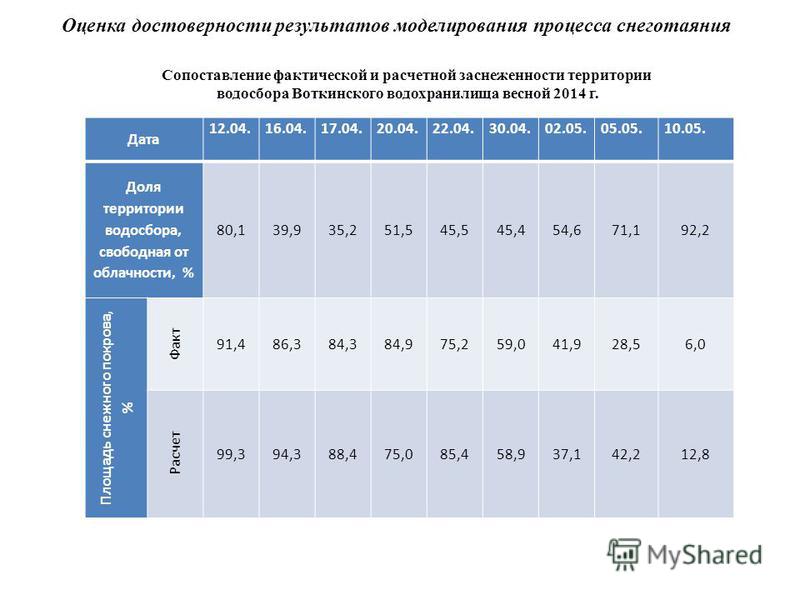
Коэффициент вариации неровности (CVm10%) на разных уровнях .
 ..
..Context 1
… коэффициенты вариации неровности (CVm% и CV10m%) кольцевой пряжи с линейной плотностью 20tex равны приведены в Таблице III. Влияние износа, размера проставки и твердости резиновой колыбели на коэффициент вариации неровности показано на Рисунках 3 и 4. Из Рисунков 3 и 4 видно, что размер проставки и твердость резиновой колыбели имеют одинаковый эффект. на CVm (%) и CV10m (%) как на неравномерности.Коэффициент вариации неровности уменьшается с увеличением размера проставки. Это может быть связано с изменением когезионных сил между волокнами, которые имеют тенденцию более плавно ослаблять узел волокон. CVm (%) и CV10m (%) также увеличиваются в результате увеличения твердости резиновой кроватки. Уравнения регрессии для коэффициента неравномерности приведены в таблице V. Значение R 2 уравнения регрессии для CVm (%) и CV10m (%) составляет 79,74 и 97,79 процентов. …
Контекст 2
… Коэффициенты вариации неровности (CVm% и CV10m%) кольцевой пряжи с линейной плотностью 20tex приведены в Таблице III. Влияние износа, размера проставки и твердости резиновой колыбели на коэффициент вариации неровности показано на Рисунках 3 и 4. Из Рисунков 3 и 4 видно, что размер проставки и твердость резиновой колыбели имеют одинаковый эффект. на CVm (%) и CV10m (%) как на неравномерности. Коэффициент вариации неровности уменьшается с увеличением размера проставки.Это может быть связано с изменением когезионных сил между волокнами, которые имеют тенденцию более плавно ослаблять узел волокон. CVm (%) и CV10m (%) также увеличиваются в результате увеличения твердости резиновой кроватки. Уравнения регрессии для коэффициента неравномерности приведены в таблице V. Значение R 2 уравнения регрессии для CVm (%) и CV10m (%) составляет 79,74 и 97,79 процентов. …
Context 3
… Коэффициенты вариации неровности (CVm% и CV10m%) кольцевой пряжи с линейной плотностью 20tex приведены в таблице III.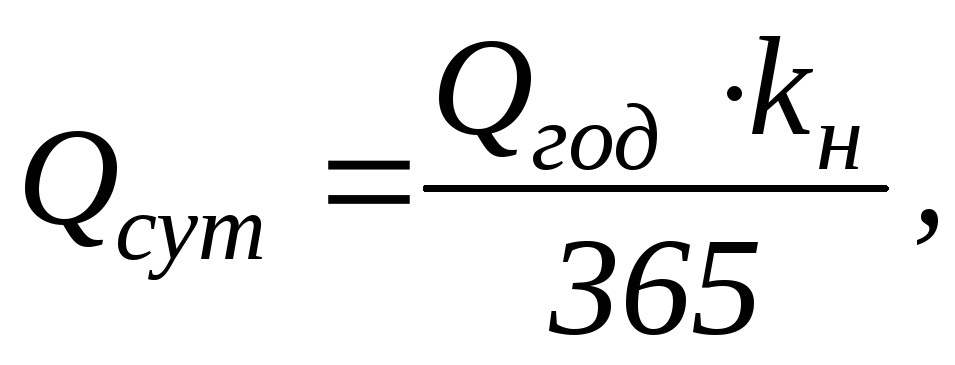 Влияние износа, размера проставки и твердости резиновой колыбели на коэффициент вариации неровности показано на Рисунках 3 и 4. Из Рисунков 3 и 4 видно, что размер проставки и твердость резиновой колыбели имеют одинаковый эффект. на CVm (%) и CV10m (%) как на неравномерности. …
Влияние износа, размера проставки и твердости резиновой колыбели на коэффициент вариации неровности показано на Рисунках 3 и 4. Из Рисунков 3 и 4 видно, что размер проставки и твердость резиновой колыбели имеют одинаковый эффект. на CVm (%) и CV10m (%) как на неравномерности. …
Контекст 4
… влияние разрыва, размера проставки и твердости резиновой колыбели на коэффициент вариации неровности показано на Рис. 3 и Рис. 4. Это видно из Рис. 3 и Рис. На рис. 4 видно, что размер проставки и твердость резиновой колыбели имеют такое же влияние на CVm (%) и CV10m (%), что и на неровность.Коэффициент вариации неровности уменьшается с увеличением размера проставки. …
Математическое выражение неровностей пряжи
Студент Университета текстиля Бангладеш (BUTEX) Отдел: Швейная инженерия
Последние сообщения Md Sohanur Rahman Sobuj (посмотреть все)
Неравномерность и коэффициент вариации пряжи
Ровность пряжи-1 Ровность пряжи-2 Ровность пряжи-3 Ровность пряжи-4
Математическое выражение неоднородности пряжи или вариации массы
Обычно используются два параметра, чтобы выразить неравномерность пряжи.Они…
- 1. Процент среднего отклонения (PMD) или неравномерности (U%)
- 2. Коэффициент вариации CV%
Процент среднего отклонения (PMD) или неравномерности (U%)
Среднее значение для всех отклонений от среднего, которое выражается в процентах от общего среднего, называется процентом среднего отклонения (PMD). Компания Uster называет это U m %.
Коэффициент вариации массы (CV%):
Коэффициент вариации массы CV% — это отношение стандартного отклонения вариации массы к средней вариации массы.Чем выше значение CV, тем неровнее пряжа.
Современный прибор, такой как тестер равномерности Uster, может измерять значения U и CV узла волокна на высокой скорости. Большие отклонения от среднего значения гораздо более интенсивно учитываются при вычислении CV%, а не U% (из-за возведения члена в квадрат). По этой причине коэффициент вариации CV% получил большее признание в современной статистике
Большие отклонения от среднего значения гораздо более интенсивно учитываются при вычислении CV%, а не U% (из-за возведения члена в квадрат). По этой причине коэффициент вариации CV% получил большее признание в современной статистике
, чем значение отклонения U%.
Связь между процентом среднего отклонения (PMD) и коэффициентом вариации CV%
Если требуется испытать узел волокна в с нормальным распределением в отношении изменения массы, то два параметра неоднородности связаны следующим уравнением:
| Тип волоконной сборки | Коэффициент преобразования |
► Нормальное распределение (содержит чисто случайные вариации, симметричное) ►Асимметричное распределение, периодические и случайные вариации (неверный тестовый материал e.грамм. с длинноволновыми вариациями счета, утолщениями и т. д.) ►Симметричное распределение с сильными периодическими вариациями | 1,25
<1,25 Виагра для здоровья |
(8220)
Студент Университета текстиля Бангладеш (BUTEX) Отдел: Швейная инженерия
Последние сообщения Md Sohanur Rahman Sobuj (посмотреть все)
Коэффициент неравномерности| Научный.Нетто
Расчет водной экологической емкости приливных участков в устьевых районах на основе неравномерного коэффициентаАвторы: Ци Чжоу, Юн Пан
Резюме: В связи с возвратно-поступательным течением приливных участков в устьевых зонах и неравномерным горизонтальным распределением в процессе переноса загрязняющих веществ в данной диссертации предлагается метод расчета водоемкости на основе модели возвратно-поступательного течения и метода неравномерности коэффициентов.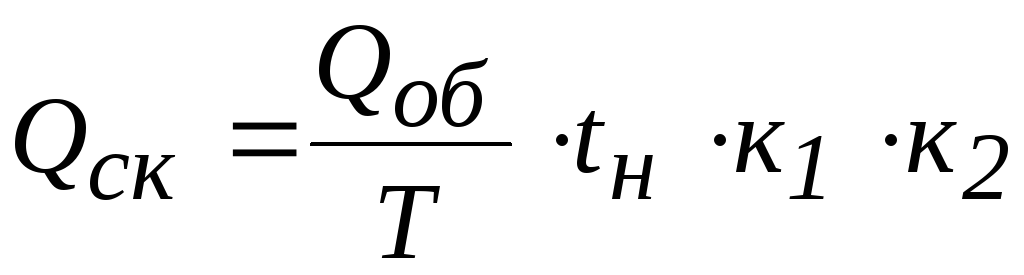 На примере Северного канала, ниже по течению реки Мин, установлена двухмерная модель качества воды в неустойчивом состоянии. В соответствии с его гидрологическими характеристиками и датой измерения моделируются поле стока и поле концентрации этого участка реки, а тем временем кривая зависимости отклика пропускной способности этих общих источников загрязняющих веществ в зависимости от протяженности зон загрязнения в моменты максимального паводка. прилив и отлив, построен. Кроме того, Северный канал разделен на два исследуемых участка, коэффициенты неравномерного распределения которых в указанные два момента рассчитываются соответственно.Учитывая надежность, неравномерные коэффициенты при приливе и отливе заменяются коэффициентами в момент максимального прилива и максимального прилива, и на основе модели возвратно-поступательного течения применяется метод неравномерных коэффициентов для расчета водоемкости окружающей среды. Северный канал. Полученные данные показывают, что, приняв двухмерную модель неустойчивого состояния качества воды, рассчитанные таким образом значения поля стока и поля концентрации на этом участке реки приближаются к измеренным значениям.Выбирается поверхностный поток с достоверностью 90% и берется образец в качестве пробы, емкость водной среды COD Mn в Северном канале составляет 16716,8 т / год. Этот метод вместе с моделью возвратно-поступательного потока и методом неравномерного коэффициента отражает влияние возвратно-поступательного потока. и сложная миграция и распространение загрязнений под действием приливов на водную среду приливных участков в устьевых районах.
На примере Северного канала, ниже по течению реки Мин, установлена двухмерная модель качества воды в неустойчивом состоянии. В соответствии с его гидрологическими характеристиками и датой измерения моделируются поле стока и поле концентрации этого участка реки, а тем временем кривая зависимости отклика пропускной способности этих общих источников загрязняющих веществ в зависимости от протяженности зон загрязнения в моменты максимального паводка. прилив и отлив, построен. Кроме того, Северный канал разделен на два исследуемых участка, коэффициенты неравномерного распределения которых в указанные два момента рассчитываются соответственно.Учитывая надежность, неравномерные коэффициенты при приливе и отливе заменяются коэффициентами в момент максимального прилива и максимального прилива, и на основе модели возвратно-поступательного течения применяется метод неравномерных коэффициентов для расчета водоемкости окружающей среды. Северный канал. Полученные данные показывают, что, приняв двухмерную модель неустойчивого состояния качества воды, рассчитанные таким образом значения поля стока и поля концентрации на этом участке реки приближаются к измеренным значениям.Выбирается поверхностный поток с достоверностью 90% и берется образец в качестве пробы, емкость водной среды COD Mn в Северном канале составляет 16716,8 т / год. Этот метод вместе с моделью возвратно-поступательного потока и методом неравномерного коэффициента отражает влияние возвратно-поступательного потока. и сложная миграция и распространение загрязнений под действием приливов на водную среду приливных участков в устьевых районах.
790
Интегральная корреляция для неоднородных и по-разному отобранных данных и ее применение к климатической записи Law Dome в Антарктике
Тестовые примеры
Мы рассматриваем несколько тестовых примеров для оценки производительности алгоритма SLICK по сравнению с корреляцией ядра Гаусса. Мы исключаем корреляцию Пирсона из тестовых примеров, поскольку было показано, что корреляция ядра Гаусса превосходит ее 4 . Первый тестовый пример предназначен для кусочно-линейных функций, вдохновленный одним из авторов, у которого возникли трудности с корреляцией ядра Гаусса при анализе данных радара проникающего льда с сигналами этой общей формы. Второй пример — корреляция между тригонометрическими функциями, которые распространены во многих областях исследования. Чтобы позволить прямое сравнение между нашим новым методом и корреляцией ядра Гаусса, мы затем рассмотрим два примера из Rehfeld et al. 4 с использованием функциональных форм, общих для климатических исследований, двух случаев авторегрессии и синусоид со случайной фазой, где корреляция ядра Гаусса хорошо работает по сравнению с другими методами.
Мы исключаем корреляцию Пирсона из тестовых примеров, поскольку было показано, что корреляция ядра Гаусса превосходит ее 4 . Первый тестовый пример предназначен для кусочно-линейных функций, вдохновленный одним из авторов, у которого возникли трудности с корреляцией ядра Гаусса при анализе данных радара проникающего льда с сигналами этой общей формы. Второй пример — корреляция между тригонометрическими функциями, которые распространены во многих областях исследования. Чтобы позволить прямое сравнение между нашим новым методом и корреляцией ядра Гаусса, мы затем рассмотрим два примера из Rehfeld et al. 4 с использованием функциональных форм, общих для климатических исследований, двух случаев авторегрессии и синусоид со случайной фазой, где корреляция ядра Гаусса хорошо работает по сравнению с другими методами.
Кусочно-линейная
Рассмотрим кусочно-линейную функцию линейного нарастания с шагом, происходящим в области длиной 0,1, заданной следующим образом:
$$ \ begin {align} f (x) = \ left \ {\ begin {array} {ll} 0 & {} \ hbox {if} 0 (5) Мы генерируем временные ряды путем повторной выборки вышеуказанной функции с использованием равномерной случайной выборки, всего с 11 точками, по крайней мере две из которых должны лежать в диапазоне [4.9,5.0]. Коэффициент корреляции для любых двух временных рядов должен быть 1. Чтобы собрать статистику о производительности SLICK, мы повторяем процесс для ансамбля из 100 членов и сравниваем результаты с корреляцией ядра Гаусса (рис.1а). Графики прямоугольных усов показывают крайние корреляции ансамбля и корреляции квартилей ансамбля. Теоретическая корреляция показана кружком. ( a ) Кусочно-линейный случай (обратите внимание, даже наихудшая корреляция SLICK лучше, чем более 75% результата ядра Гаусса). Рассмотрим коэффициент корреляции Пирсона между двумя функциями \ (\ cos (x) \) и \ (\ sin (x) \) на интервале \ ((0, \ pi / 2) \ ). Ожидаемый коэффициент корреляции Пирсона между этими двумя рядами можно оценить с помощью дискретной выборки в предельном случае бесконечного числа дискретных выборок: $$ \ begin {align} \ frac {1 / 2-2 / \ pi} {\ left (\ pi / 4-2 / \ pi \ right)} \ приблизительно -0,918. \ end {align} $$ (6) Мы оцениваем точность двух разных алгоритмов для неравномерно и по-разному отобранных данных и сравниваем с классическим алгоритмом для равномерно и идентично отобранных данных на рис.1b. Чтобы гарантировать результаты, соответствующие формуле. 6 мы явно включаем точки в крайних точках диапазона (т.е. 0 и \ (\ pi / 2 \)). Чтобы оценить надежность оценок, мы повторяем вычисления для 1000 членов ансамбля, используя равномерную случайную повторную выборку, и показываем среднее, стандартное отклонение и экстремальные значения для ансамблей (рис. 1b). Рассмотрим функцию авторегрессии AR (1), типичную для многих климатических процессов, следующим образом: $$ \ begin {align} X (t_ {i + 1}) = \ exp \ left (- \ frac { t_ {i + 1} -t_i} {\ ln \ phi} \ right) X (t_i) + \ epsilon _i, \ end {align} $$ (7) где \ (\ phi \) — коэффициент AR (1) и \ (\ epsilon _i \) некоррелированный гауссовский распределенный шум. Автокорреляция с опережением или запаздыванием на одну единицу времени должна равняться \ (\ phi \). Мы тестируем это, используя ансамбль из 100 членов, каждый из которых представляет собой временной ряд продолжительностью 1000 лет, выбранный по времени с интервалом 5 с распределением по гамме со средним значением один год и асимметрией 2,85. Результаты показаны на рис. 1c, d. Для меньшей автокорреляции лаг-1, равной 0,7, более 50% результатов SLICK находятся в пределах 0,026 от правильного результата, в то время как 50% результатов корреляции ядра Гаусса имеют ошибку более чем на 0.081. Для большей автокорреляции лаг-1, равной 0,9, SLICK по-прежнему превосходит корреляцию ядра Гаусса, причем более 75% результатов SLICK лучше, чем лучшие 25% корреляции ядра Гаусса. Однако результаты SLICK не так хороши, как для автокорреляции с более низким лагом-1. В этом случае правильный результат находится в наивысшем квартиле результатов SLICK, но это лучше, чем корреляция ядра Гаусса, когда диапазон результатов не охватывает правильное значение. Мы также показываем результаты BINCOR 2 для этого тестового примера.BINCOR выполняет повторную выборку двух авторегрессионных серий на идентичную и равномерно выбранную основу, а затем применяет стандартные методы для однородно выбранных данных. BINCOR переоценивает корреляцию для обоих тестовых случаев авторегрессии, при этом диапазон оценок ансамбля не включает правильное значение. Последний тестовый пример представляет собой сумму трех синусоид одинаковой амплитуды, со случайной фазой и периодами 18, 21 и 41 года соответственно. Эпоха составляет 1000 лет, а средняя частота дискретизации — четыре года с различной степенью перекоса по гамма-распределению.Мы снова используем ансамбль из 100 членов со случайной повторной выборкой, чтобы оценить эффективность корреляции SLICK. Ошибка автокорреляции как функция запаздывания для случайного синусоидального случая фазы, показывающего SLICK (темные сплошные и пунктирные линии и затенение) и ядро Гаусса (светлые сплошные и пунктирные линии и затемнение), медиана (сплошная линия ), межквартильный диапазон (штриховка) и крайний (пунктирные и штриховые линии) для ансамбля из 100 членов. Асимметрия составляет ( a ) 1,0, ( b ) 2. Чтобы убедиться, что предполагаемая скорость накопления снега на DE08 является разумной, мы используем метод корреляции SLICK для отслеживания внутренних слоев в данных радара прохождения льда в этом регионе. Известно, что внутренние слои в ледяном щите возникают из-за изменений химического состава льда, связанных с изменениями в составе атмосферы (такими как изменения содержания серы в атмосфере, связанные с извержениями вулканов), и поэтому могут представлять изохроны отложения снега на поверхности 10 .Последующая адвекция этих изохрон на глубину в первую очередь является функцией локальной скорости накопления снега и изменений в динамике ледникового покрова. Сильный внутренний отражатель на глубине примерно 435 м в DSS отслеживается (рис. 6) путем оптимизации корреляции SLICK относительно эталонного отражателя для небольших вертикальных окон (размером примерно 54 м), центрированных вокруг отражателя, для отдельных вертикальных срезов через радарограмма.Допускается малый масштабный коэффициент (0,98–1,02) и вертикальное смещение (от — 2,54 до 2,54 м на вертикальный срез). Локальная корреляция, превышающая пороговое значение (r = 0,85), приводит к «совпадению» и обновлению эталонного отражателя (обновляется до 95% текущего эталонного отражателя и 5% окна от текущего вертикального среза), в то время как локальная корреляция ниже этого приведет к пропуску этого вертикального среза и поиску по большему вертикальному смещению. Профиль радара между DSS (слева от изображения) и DE08 (справа от изображения).Прослеженный внутренний слой соответствует серии извержений вулканов 1257 г. н.э. Профили радара от 4 разных полетов сшиваются вместе (полетные сегменты отмечены вверху изображения). Расстояние по горизонтали составляет примерно 33,75 км, а масштаб по вертикали увеличен в 10 раз. Слой, выбранный на отметке около 435 м на DSS, соответствует извержению вулкана Самалас в 1257 году н.э. 8,15 , измеренному на глубине около 418 м в ледяном керне DSS относительно поверхности льда 1988 года.{-1} \) для DSS и DE08, соответственно, дает эффективный коэффициент линейного масштабирования 0,606. Из-за градиента накопления снега через Ло Доум и горизонтального движения льда от вершины купола, что приводит к более глубокому льду на DE08, берущему начало ближе к вершине купола (и, следовательно, в более низком месте скопления снега), мы могли бы ожидать накопления снега. Для рассмотрения случая, когда внутренние слои трудно отследить на всем расстоянии между двумя интересующими участками (возможно, из-за наклона самолета или особенностей поверхности снега), мы также оцениваем скорость накопления снега и скорость вертикальной деформации на DE08 с помощью оптимизация корреляции между профилями радара на этих двух участках.{-1} \) на DE08. Расчетная скорость накопления снега немного меньше, чем оценка по записям ледяных кернов, но включает более старый лед, который первоначально был отложен ближе к DSS (и со временем продвигался вниз по течению), поэтому мы ожидаем более низкой расчетной скорости накопления снега. на глубине. Профили отражения радара в DSS (черный) и DE08 (серый). Глубины были ограничены на обоих участках и масштабированы на DE08 с помощью обратного отношения скорости накопления снега (0.544). () (Институт сельскохозяйственной инженерии, Вроцлавский университет наук об окружающей среде и биологии, улица Chełmońskiego 37b, 51-630 Вроцлав, Польша) () (Институт сельскохозяйственной инженерии, Вроцлавский университет наук об окружающей среде и биологии, ул. Хелмоньского 37b, 51-630 Вроцлав, Польша) Целью исследования было определить влияние выбранных факторов на среднюю степень покрытия и равномерность покрытия жидкостью при помощи выбранных одинарных и двойных плоских форсунок.Было изучено влияние типа форсунки, давления распыления, скорости движения и угла распыления на среднюю степень покрытия и коэффициент неровности покрытия. Исследование проводилось с использованием специального оборудования для опрыскивания, спроектированного и сконструированного для контроля и изменения высоты штанги, угла опрыскивания, скорости движения и давления опрыскивания. Основываясь на результатах исследования, было обнаружено, что самый высокий средний охват был получен для одинарных стандартных плоских веерных форсунок и двойных плоских форсунок, предотвращающих снос. В то же время у этих насадок наблюдались самые высокие значения неравномерности.Обратные зависимости были получены для воздухозаборных сопел. Максимального покрытия с одновременной минимизацией неравномерности можно достичь, используя средний размер капель для одинарных плоских веерных форсунок (средний объемный диаметр (VMD) = 300 мкм) и крупный размер капель для двойных плоских веерных форсунок (VMD = 352 мкм), при этом низкая скорость движения (соответственно 1,1 м ∙ с −1 и 1,6 м ∙ с −1) и угол наклона сопла на 20 ° в направлении, противоположном направлению движения. Все материалы на этом сайте предоставлены соответствующими издателями и авторами. Вы можете помочь исправить ошибки и упущения.При запросе исправления укажите идентификатор этого элемента: RePEc: gam: jagris: v: 11: y: 2021: i: 2: p: 151-: d: 498490 . См. Общую информацию о том, как исправить материал в RePEc. По техническим вопросам, касающимся этого элемента, или для исправления его авторов, заголовка, аннотации, библиографической информации или информации для загрузки, обращайтесь: (Команда по преобразованию XML). Общие контактные данные провайдера: https://www.mdpi.com/ . Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь.Это позволяет связать ваш профиль с этим элементом. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которых мы не уверены. У нас нет ссылок на этот товар. Вы можете помочь добавить их, используя эту форму . Если вам известно об отсутствующих элементах, цитирующих этот элемент, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылочного элемента. Если вы являетесь зарегистрированным автором этого элемента, вы также можете проверить вкладку «Цитаты» в своем профиле RePEc Author Service, поскольку там могут быть некоторые цитаты, ожидающие подтверждения. Обратите внимание, что исправления могут занять пару недель, чтобы отфильтровать
различные сервисы RePEc. ИСТОРИЯ И ЦЕЛЬ: Диффузионно-взвешенная визуализация (DWI) позволяет раннее обнаружение и количественную оценку гипоксически-ишемических (HI) поражений головного мозга. Наша цель состояла в том, чтобы оценить прогностическую ценность измерений DWI и кажущегося коэффициента диффузии (ADC) для исходов у детей с перинатальной асфиксией. МАТЕРИАЛЫ И МЕТОДЫ: Доношенным новорожденным была проведена МРТ в течение 10 дней после рождения из-за асфиксии. МРТ-исследования были ретроспективно оценены на предмет повреждения головного мозга HI. ADC измеряли в 30 стандартизированных областях мозга и в областях с видимыми отклонениями на DWI. У выживших результаты развития до раннего школьного возраста классифицировались по следующим категориям: 1) нормальный, 2) умеренно ненормальный и 3) определенно ненормальный. Для анализа категория 3 и смерть (категория 4) были помечены как «неблагоприятные», 1 и 2 — «благоприятные», а 2–3 и смерть — «аномальный» исход.Различия в результатах между младенцами с аномалиями DWI и без них были проанализированы с использованием тестов χ 2 . Непараметрический тест Манна-Уитни U анализировал, коррелируют ли значения ADC в видимых отклонениях DWI с возрастом при визуализации. Логистический регрессионный анализ проверил прогностическую ценность результатов ADC в каждой стандартизированной области мозга. Анализ рабочих характеристик приемника использовался для нахождения оптимальных значений отсечки АЦП для каждой области для различных результатов. РЕЗУЛЬТАТЫ: Было включено 24 младенца (13 мальчиков). Средний возраст на МРТ составлял 4,3 дня (от 1 до 9 дней). Семь младенцев умерли. Не было различий в результатах между младенцами с видимыми аномалиями DWI и без них. Только ADC задней конечности внутренней капсулы коррелировал с возрастом. ADC в явно аномальных областях DWI не имел прогностической ценности для результата. Из всех выполненных измерений только ADC в базальных ганглиях и стволе мозга, которые выглядят нормально, достоверно коррелировали с исходом; низкие значения ADC были связаны с аномальным / неблагоприятным исходом, а более высокие значения ADC — с нормальным / благоприятным исходом (базальные ганглии: P =.03 для аномального, P = 0,01 для неблагоприятного исхода; ствол мозга: P = 0,006 для аномального, P = 0,03 для неблагоприятного исхода). ВЫВОДЫ. Значения ADC в базальных ганглиях и стволе мозга с нормальным внешним видом коррелировали с исходом, независимо от всех результатов МРТ, включая данные DWI. Значения ADC в явно аномальной мозговой ткани на DWI не показали прогностической ценности для результата. Описание структуры древостоя представляет большой интерес в современном лесоводстве, так как разновозрастные древостои большой сложности обладают полезными свойствами.В этой статье предлагается новый простой индекс, полученный на основе различий внутри пар соседних деревьев, который изучается путем моделирования. Индекс, названный «коэффициентом несходства», представляет собой отношение между разницей и суммой размеров в парах. Он варьируется от 0 до 1 и имеет значение 0,5, когда размеры отображаются независимо от экспоненциального распределения. Коэффициент используется для измерения пространственных вариаций в распределении размеров. На практическом примере показано, что стойка, которая в целом имеет большой разброс по диаметру, может иметь очень ограниченную общую локальную вариацию.В таких случаях этот коэффициент может быть использован для выявления пространственного распределения неровностей и агрегации. Коэффициент также может иметь значение для исследований экосистем, отличных от лесной. Журнал сельскохозяйственной, биологической и экологической статистики (JABES), публикуемый ежеквартально с 1996 года, является совместным изданием Американской статистической ассоциации и Международного биометрического общества. Журнал способствует развитию и использованию статистических методов в сельскохозяйственных науках, биологических науках (включая биотехнологии) и науках об окружающей среде (включая те, которые имеют дело с природными ресурсами).Опубликованные статьи имеют непосредственную практическую ценность для прикладных исследователей и статистических консультантов в этих областях, поскольку рассматриваются только статьи, посвященные прикладным статистическим проблемам. Настоятельно рекомендуется использовать междисциплинарные статьи, а также статьи, иллюстрирующие применение новых важных статистических методов с использованием реальных данных. Разъяснительные, обзорные и обзорные статьи, посвященные широким статистическим вопросам, считаются особенно ценным вкладом журнала в практических и прикладных статистиков.Отличительной особенностью JABES является то, что он требует от автора включения исходных данных, чтобы другие могли немедленно применить интересующий статистический метод (ы). Springer — одна из ведущих международных научных издательских компаний, издающая более 1200 журналов и более
3000 новых книг ежегодно, охватывающих широкий круг предметов, включая биомедицину и науки о жизни, клиническую медицину,
физика, инженерия, математика, компьютерные науки и экономика.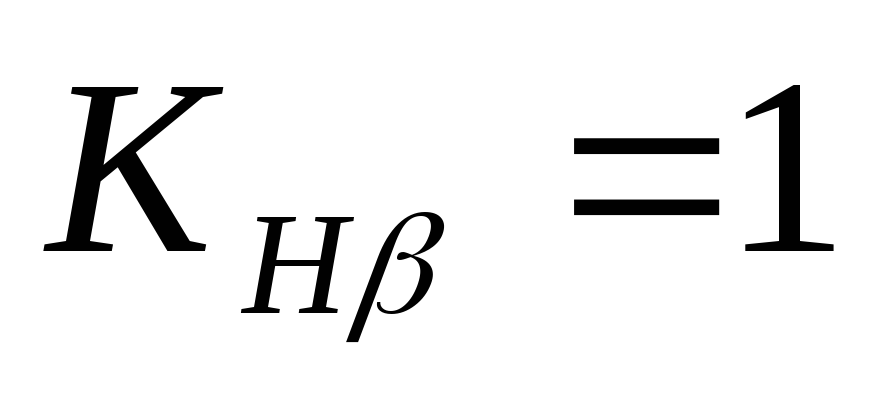 ( b ) Случай тригонометрических функций. ( c ) Случай авторегрессии для автокорреляции с лаг-1 0,7. ( d ) Случай авторегрессии для автокорреляции lag-1, равной 0.9.
( b ) Случай тригонометрических функций. ( c ) Случай авторегрессии для автокорреляции с лаг-1 0,7. ( d ) Случай авторегрессии для автокорреляции lag-1, равной 0.9. Тригонометрические функции
Авторегрессия

Синусоиды со случайной фазой
 {- 3} \)), и все глубины указаны как «глубины, эквивалентные льду» (IE).{18} \) O измерения до 25 мм по сравнению с глубиной соседних измерений. Чтобы оптимизировать линейную модель и мелкомасштабные поправки, мы систематически изменяем эти параметры, чтобы максимизировать коэффициент корреляции Пирсона (r = 0,827), рассчитанный с помощью SLICK. Поскольку SLICK не требует равной или одинаковой выборки между двумя сериями, применение линейной модели с мелкомасштабными поправками требует только пересчета глубины выборки, а не линейной интерполяции данных, которая может вызвать смещения 1 .{-1} \), основанный на записи за 2000 год 7 , и оценил скорость деформации DE08 путем оптимизации точной коррекции масштаба. В частности, когда поправки для скоростей деформации DSS и DE08 неверны (или не применяются вообще), в мелкомасштабной поправке будет крупномасштабная структура, в то время как последовательная комбинация скоростей деформации приведет к небольшим поправкам с немного большим масштабная структура. Например, на рис. 4 отчетливо видно влияние поправки на скорость вертикальной деформации.{18} \) O) запись для DSS (серый) и переназначенная глубина DE08 (черный). Корреляция между этими двумя записями составляет r = 0,827.
{- 3} \)), и все глубины указаны как «глубины, эквивалентные льду» (IE).{18} \) O измерения до 25 мм по сравнению с глубиной соседних измерений. Чтобы оптимизировать линейную модель и мелкомасштабные поправки, мы систематически изменяем эти параметры, чтобы максимизировать коэффициент корреляции Пирсона (r = 0,827), рассчитанный с помощью SLICK. Поскольку SLICK не требует равной или одинаковой выборки между двумя сериями, применение линейной модели с мелкомасштабными поправками требует только пересчета глубины выборки, а не линейной интерполяции данных, которая может вызвать смещения 1 .{-1} \), основанный на записи за 2000 год 7 , и оценил скорость деформации DE08 путем оптимизации точной коррекции масштаба. В частности, когда поправки для скоростей деформации DSS и DE08 неверны (или не применяются вообще), в мелкомасштабной поправке будет крупномасштабная структура, в то время как последовательная комбинация скоростей деформации приведет к небольшим поправкам с немного большим масштабная структура. Например, на рис. 4 отчетливо видно влияние поправки на скорость вертикальной деформации.{18} \) O) запись для DSS (серый) и переназначенная глубина DE08 (черный). Корреляция между этими двумя записями составляет r = 0,827. Отслеживание внутренних слоев антарктического ледяного щита
 {- 1} \) во льду и без учета эффектов фирна. .Чтобы дать возможность интерпретировать особенности радиолокационного сигнала с точки зрения химического состава ледяного ядра, мы преобразуем радиолокационный сигнал из временной области в глубинную. Поскольку SLICK не зависит от основы выборки (только относительное расстояние между выборками), это преобразование в область глубины не меняет корреляции.
{- 1} \) во льду и без учета эффектов фирна. .Чтобы дать возможность интерпретировать особенности радиолокационного сигнала с точки зрения химического состава ледяного ядра, мы преобразуем радиолокационный сигнал из временной области в глубинную. Поскольку SLICK не зависит от основы выборки (только относительное расстояние между выборками), это преобразование в область глубины не меняет корреляции.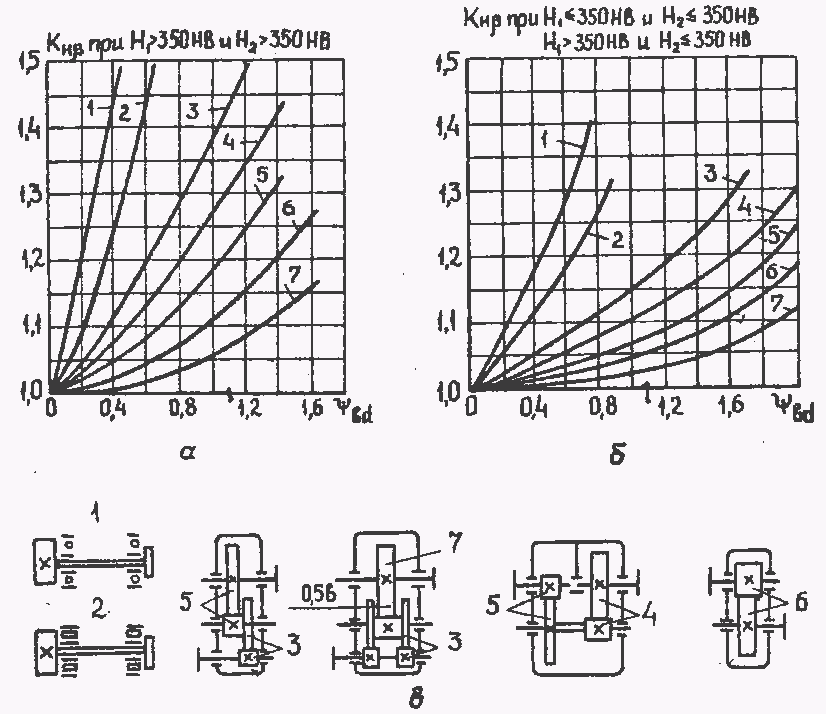 соотношение будет больше, чем мы нашли, используя записи ледяных кернов.
соотношение будет больше, чем мы нашли, используя записи ледяных кернов. Средняя степень покрытия и коэффициент неравномерности покрытия как параметры для оценки качества распыления
Автор
Перечислено: Abstract
Рекомендуемое цитирование
Скачать полный текст от издателя
Исправления
Предсказывают ли измерения кажущегося коэффициента диффузии исход у детей с неонатальной гипоксически-ишемической энцефалопатией?
Abstract
Коэффициент для описания разницы в размере между соседними деревьями в JSTOR
Реферат
 т.
т. т.
т. ткм брутто/сутки
ткм брутто/сутки