Создание дерева решений (блок-схемы) в Excel

 

Добрый день.
Как Вы наверняка знаете «Excel» —  это не только инструмент для математических расчетов и аналитики числовых данных, но и прекрасный инструмент для оформления документов и создания схем взаимодействия (бизнес-схем).
В поздних версиях программы «Excel» созданы специальные опции для создания и редактирования древовидных схем (план-схем, алгоритмов). Таких как, так называемое, дерево решений.
Дерево решений – это схема, представляющая собой набор связанных между собой в виде дерева блоков. Каждому из блоков в дереве решений присваивается действие (решение). Соответственно, при выполнении того или иного действия появляются несколько вариантов новых решений и т.д.

Пример дерева решений: «Поход в магазин за покупками»

Создать такое дерево решений довольно просто при помощи кнопки SmartArt («умное творчество»).

Кнопка  SmartArt находится во вкладке «Вставка». После клика по указанной кнопке появляется окно, в котором предложены десятки готовых решений (структур) схемы.

Для дерева решений оптимально подходят готовые структуры и раздела «Иерархия».

Выбрав понравившуюся структуру, при помощи опций из вкладки «Конструктор» можно сформировать необходимой дерево действия.

 

При помощи кнопки «Добавить фигуру» можно добавлять новые блоки.

Кнопками «повысить уровень» и «понизить уровень» можно менять место блока в структуре.

Кнопка «Область текста» открывает окно для работы с надписями в блоках.

Так же раздел «конструктор» позволяет редактировать внешний вид блоков:

 

Цвета схемы

 

Способ отображения блоков, в том числе и 3D вид дерева решений.

 

 

Программа для построения древо решений — Edraw

Деревья решений широко используются, чтобы помочь сделать правильный выбор во многих различных дисциплинах, включая медицинский диагноз, когнитивную науку, искусственный интеллект, теорию программ, инженерию и интеллектуальный анализ данных.

Введение для построения  древа решений

Деревья решений — отличные инструменты, которые помогут вам сделать выбор между несколькими способами действий. Они обеспечивают высокоэффективную структуру, в рамках которой вы можете выстраивать варианты и исследовать возможные результаты выбора этих вариантов. Они также помогут вам сформировать сбалансированную картину рисков и выгод.

Программа для построения  древа решений

У Edraw есть умные инструменты и символы для рисования, которые позволяют руководителю проекта, бизнес-аналитику или разработчику проекта создать древо решений с легкостью.

Узнайте, почему Edraw — идеальная программна для построения дерева решений: попробуйте БЕСПЛАТНО.

Системные Требования

Работает на Windows 7, 8, 10, XP, Vista и Citrix

Работает на 32-битных и 64-битных Windows

Работает на Mac OS X 10.2 или новее

Маркированы на: Матричный шаблон

Программные функции для разработки дерева решений

Создание дерева решений теперь так же просто, как 1, 2, 3.

1. Выберите шаблон, чтобы начать работу

1. Edraw имеет огромный банк готовых шаблонов дерева решений.
2. Создать персонализированные деревья решений, визуальные расписания, наградные графики, листовки и сертификаты.
3. Более 200 видов широко используемых коммуникационных устройств и шаблонов.
4. Добавьте свои собственные рисунки для создания мотивационных диаграмм или инфографики.

2. Добавить свое содержимое так же легко, как пирог

1. Выберите из наших подготовленных шаблонов и библиотек с более 8000 изображений. Поиск по ключевому слову, категории или по алфавиту с помощью нашей интеллектуальной поисковой системы.
2. Вставляйте текст в существующие текстовые поля или добавляйте текстовые поля в любое время в любом месте на полотне.
   
3. Или добавьте фотографию мгновенно с помощью функции «Вставка».
4. Вы также можете просматривать любую папку на своем компьютере, чтобы использовать свои собственные изображения. Добавьте их во встроенную библиотеку для быстрого поиска в будущем.

3. Распечатать/ Поелиться

1. Теперь легко напечатать свою работу с высокой четкостью. Или поделиться им в различных форматах. Если вам нужно отредактировать, есть простые интуитивные инструменты для использования.
2. Перетащите ваши фотографии на правое полотно.
3. Наведите и перетащите на прикрепленные кнопки, чтобы изменить их размер, перекрасить, повернуть и переместить фигуры.
4. Измените цвет изображений и фона с помощью встроенных тем.
5. Измените размер, цвет и положение текста.

Символы для построения дерева решений

Дерево решений имеет набор стандартных графических символов и условных обозначений для описания элементов. Обычно используемые символы дерева решений включают в себя узлы принятия решений, узлы случайных событий, конечные точки, ветви и метки с двойным штрихом.

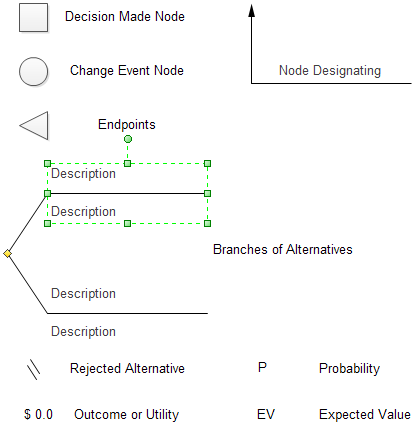
Пример дерева решений

Дополнительные примеры для управления проектов

Матрица схемы работы	Сроки Реализации Проекта	Диаграмма WBS

Вы полюбите эту идеальную программу для построения диаграмм!

Edraw Max — прекрасная программа создания блок-схемы, диаграммы связей, организационной диаграммы,сетевой диаграммы, плана этажей, потока работ, современного дизайа, UML-диаграммы, электрической схемы, научной иллюстрации и много другого!

Энтропия и деревья принятия решений / Habr

Деревья принятия решений являются удобным инструментом в тех случаях, когда требуется не просто классифицировать данные, но ещё и объяснить почему тот или иной объект отнесён к какому-либо классу.

Давайте сначала, для полноты картины, рассмотрим природу энтропии и некоторые её свойства. Затем, на простом примере, увидим каким образом использование энтропии помогает при создании классификаторов. После чего, в общих чертах сформулируем алгоритм построения дерева принятия решений и его особенности.

Комбинаторная энтропия

Рассмотрим множество разноцветных шариков: 2 красных, 5 зеленых и 3 желтых. Перемешаем их и расположим в ряд. Назовём эту операцию перестановкой:

Давайте посчитаем количество различных перестановок, учитывая что шарики одного цвета — неразличимы.

Если бы каждый шарик имел уникальный цвет, то количество перестановок было бы 10!, но если два шарика одинакового цвета поменять местами — новой перестановки не получится. Таким образом, нужно исключить 5! перестановок зеленых шариков между собой (а также, 3! желтых и 2! красных). Поэтому, в данном случае, решением будет:

Мультиномиальний коэффициент позволяет рассчитать количество перестановок в общем случае данной задачи: (Ni — количество одинаковых шариков каждого цвета).

Все перестановки можно пронумеровать числами от

0 до (W — 1). Следовательно, строка из log₂(W) бит однозначно кодирует каждую из перестановок.

Поскольку перестановка состоит из N шариков, то среднее количество бит, приходящихся на один элемент перестановки можно выразить как:

Эта величина называется комбинаторной энтропией:

Чем более однородно множество (преобладают шарики какого-то одного цвета) — тем меньше его комбинаторная энтропия, и наоборот — чем больше различных элементов в множестве, тем выше его энтропия.

Энтропия Шеннона

Давайте рассмотрим подробнее описанное выше выражение для энтропии:

Учитывая свойства логарифмов, преобразуем формулу следующим образом:

Предположим, что количество шариков достаточно велико для того чтобы воспользоваться формулой Стирлинга:

Применив формулу Стирлинга, получаем:

(где k — коэффициент перехода к натуральным логарифмам)

Учитывая что выражение можно преобразовать:

Поскольку общее количество шариков N, а количество шариков i-го цвета — Ni, то вероятность того, что случайно выбранный шарик будет именно этого цвета является: . Исходя из этого, формула для энтропии примет вид:

Данное выражение является энтропией Шенонна.

При более тщательном выводе можно показать, что энтропия Шенонна является пределом для комбинаторной энтропии, поэтому её значение всегда несколько больше значения комбинаторной энтропии.

Сравнение двух энтропий представлено на следующем рисунке, который рассчитан для множеств, содержащих два типа объектов — А и В (суммарное количество элементов в каждом множестве — 100):

Термодинамика

Аналогичные выражения для энтропии можно получить в термодинамике:

• Исходя из микроскопических свойств веществ: опираясь на постулаты статистической термодинамики (в данном случае оперируют неразличимыми частицами, которые находятся в разных энергетических состояниях).
  
• Исходя из макроскопических свойств веществ: путем анализа работы тепловых машин.
  

Понятие энтропии играет фундаментальную роль в термодинамике, фигурируя в формулировке Второго начала термодинамики:

если изолированная макроскопическая система находится в неравновесном состоянии, то наиболее вероятным является её самочинный переход в состояние с большим значением энтропии:

Демон Максвелла

Чтобы подчеркнуть статистическую природу Второго начала термодинамики в 1867 году Джеймс Максвелл предложил мысленный эксперимент: «Представим сосуд, заполненный газом определённой температуры, сосуд разделен перегородкой с заслонкой, которую демон открывает чтобы пропускать быстрые частицы в одну сторону, а медленные — в другую. Следовательно, спустя некоторое время, в одной части сосуда сконцентрируются быстрые частицы, а в другой — медленные. Таким образом, вопреки Второму началу термодинамики, демон Максвелла может уменьшать энтропию замкнутой системы»:

Позже, Лео Сциллард разрешил парадокс, но это обсуждение несколько выходит за рамки данной статьи.

Демон Максвелла == Классификатор

Если вместо «быстрых» и «медленных» частиц рассматривать объекты, принадлежащие к различным классам, тогда демона Максвелла можно рассматривать в качестве своеобразного классификатора.

Сама формулировка парадокса подсказывает алгоритм обучения: нужно находить правила (предикаты), на основе которых разбивать тренировочный набор данных, таким образом, чтобы уменьшалось среднее значение энтропии. Процесс деления множества данных на части, приводящий к уменьшению энтропии, можно рассматривать как производство информации.

Разбив исходный набор данных на две части по некому предикату, можно рассчитать энтропию каждого подмножества, после чего рассчитать среднее значение энтропии — если оно окажется меньшим чем энтропия исходного множества, значит предикат содержит некую обобщающую информацию о данных.

Для примера, рассмотрим множество двухцветных шариков, в котором цвет шарика зависит только от координаты х:
(из практических соображений, при расчётах удобно использовать энтропию Шеннона)

Из рисунка видно что если разделить множество на две части, при условии что одна часть будет содержать все элементы с координатой х ≤ 12, а другая часть — все элементы, у которых х > 12, то средняя энтропия будет меньше исходной на ∆S. Это значит, что данный предикат обобщает некоторую информацию о данных (легко заметить, что при х > 12 — почти все шарики жёлтые).

Если использовать относительно простые предикаты («больше», «меньше», «равно» и т.п.) — то, скорее всего, одного правила будет недостаточно для создания полноценного классификатора. Но процедуру поиска предикатов можно повторять рекурсивно для каждого подмножества. Критерием остановки является нулевое (или очень маленькое) значение энтропии. В результате получается древовидный набор условий, который называется Деревом принятия решений:

Листьями дерева принятия решений являются классы. Чтобы классифицировать объект при помощи дерева принятия решений — нужно последовательно спускаться по дереву (выбирая направление основываясь на значениях предикатов применяемых к классифицируемому объекту). Путь от корня дерева до листьев можно трактовать как объяснение того, почему тот или иной объект отнесён к какому-либо классу.

В рассмотренном примере, для упрощения, все объекты характеризуются только одним атрибутом — координатой х, но точно такой же подход можно применить и к объектам со множественными атрибутами.

Также, не накладывается ограничений на значения атрибутов объекта — они могут иметь как категориальную, так и числовую или логическую природу. Нужно только определить предикаты, которые умеют правильно обрабатывать значения атрибутов (например, вряд ли есть смысл использовать предикаты «больше» или «меньше» для атрибутов с логическими значениями).

Алгоритм построения дерева принятия решений

В общих чертах, алгоритм построения дерева принятия решений можно описать следующим образом:
(мне кажется, что алгоритм описанный «человеческим языком» легче для восприятия)

s0 = вычисляем энтропию исходного множества

Если s0 == 0 значит:
   Все объекты исходного набора, принадлежат к одному классу
   Сохраняем этот класс в качестве листа дерева

Если s0 != 0 значит:
   Ищем предикат, который разбивает исходное множество таким образом чтобы уменьшилось среднее значение энтропии
   Найденный предикат является частью дерева принятия решений, сохраняем его

   Разбиваем исходное множество на подмножества, согласно предикату
   Повторяем данную процедуру рекурсивно для каждого подмножества

Что значит «ищем предикат»?
Как вариант, можно считать, что на основе каждого элемента исходного множества можно построить предикат, который разбивает множество на две части. Следовательно, алгоритм можно переформулировать:

s0 = вычисляем энтропию исходного множества

Если s0 == 0 значит:
   Все объекты исходного набора, принадлежат к одному классу
   Сохраняем этот класс в качестве листа дерева

Если s0 != 0 значит:
   Перебираем все элементы исходного множества:
      На основе каждого элемента генерируем предикат, который разбивает исходное множество на два подмножества
      Рассчитываем среднее значение энтропии
      Вычисляем ∆S
   Нас интересует предикат, с наибольшим значением ∆S
   Найденный предикат является частью дерева принятия решений, сохраняем его

   Разбиваем исходное множество на подмножества, согласно предикату
   Повторяем данную процедуру рекурсивно для каждого подмножества

Как можно «на основе каждого элемента множества генерировать предикат»?
В самом простом случае, можно использовать предикаты, которые относятся только к значению какого-нибудь атрибута (например «x ≥ 12», или «цвет == жёлтый» и т.п.). Следовательно, алгоритм примет вид:

s0 = вычисляем энтропию исходного множества

Если s0 == 0 значит:
   Все объекты исходного набора, принадлежат к одному классу
   Сохраняем этот класс в качестве листа дерева

Если s0 != 0 значит:
   Перебираем все элементы исходного множества:
      Для каждого элемента перебираем все его атрибуты:
         На основе каждого атрибута генерируем предикат, который разбивает исходное множество на два подмножества
         Рассчитываем среднее значение энтропии
         Вычисляем ∆S
   Нас интересует предикат, с наибольшим значением ∆S
   Найденный предикат является частью дерева принятия решений, сохраняем его

   Разбиваем исходное множество на подмножества, согласно предикату
   Повторяем данную процедуру рекурсивно для каждого подмножества

На самом деле, если рассматривать классифицируемые объекты как точки в многомерном пространстве, то можно увидеть, что предикаты, разделяющие множество данных на подмножества, являются гиперплоскостями, а процедура обучения классификатора является поиском ограничивающих объёмов (в общем, как и для любого другого вида классификаторов).

Главным достоинством является, получаемая в результате, древовидная структура предикатов, которая позволяет интерпретировать результаты классификации (хотя в силу своей «жадности», описанный алгоритм, не всегда позволяет обеспечить оптимальность дерева в целом).

Одним из краеугольных камней описанного алгоритма является критерий остановки при построении дерева. В описанных выше псевдокодах, я прекращал построение дерева только при достижении множества, в котором все элементы принадлежат к одному классу (энтропия == 0). Такой подход позволяет полностью подогнать дерево принятия решений под обучающую выборку данных, но это не всегда эффективно с практической точки зрения (полученное дерево является переобученным).

Одним из возможных критериев остановки может быть небольшое значение ∆S. Но при таком подходе, всё же, невозможно дать универсальный совет: при каких значениях ∆S следует прекращать построение дерева.

Random forest

Чтобы не заморачиваться над критерием остановки при построении дерева, можно поступить следующим образом: выбирать случайные подмножества из обучающей выборки данных, и для каждого подмножества строить своё дерево принятия решений (в принципе, даже не важно какой критерий остановки будет использоваться):

Полученный в результате ансамбль деревьев (упрощённая версия Random forest) можно использовать для классификации, прогоняя классифицируемый объект через все деревья. Каждое дерево как будто «голосует» за принадлежность объекта к определённому классу. Таким образом, на основе того, какая часть деревьев проголосовала за тот или иной класс — можно заключить с какой вероятностью объект принадлежит к какому либо классу.

Данный метод позволяет достаточно адекватно обрабатывать пограничные области данных:

Можно заметить, что единичное дерево принятия решений описывает область, которая полностью содержит красные точки, в то время как ансамбль деревьев описывает фигуру, которая более близка к окружности.

Если есть желание поэкспериментировать

Я создал небольшое приложение, для сравнения дерева принятия решений и random forest. При каждом запуске приложения создаётся случайный набор данных, соответствующий красному кругу на зелёном фоне, а в результате выполнения приложения получается картинка, типа той, которая изображена выше.

• У Вас должна быть установлена среда выполнения Java
  
• Загрузите отсюда бинарник dec_tree_demo.jar
  
• Для запуска приложения наберите в командной строке: java -jar dec_tree_demo.jar out.png
  

Исходники есть на гитхабе.

Вместо заключения

Деревья принятия являются неплохой альтернативой, в тех случаях когда надоедает подстраивать абстрактные веса и коэффициенты в других алгоритмах классификации, либо, когда приходится обрабатывать данные со смешанными (категориальными и числовыми) атрибутами.

Дополнительная информация

1. Яцимирский В.К. Физическая химия (здесь довольно неплохо описано понятие энтропии, а также рассматриваются некоторые философские аспекты данного феномена)
   
2. Интересный тред про сжатие и энтропию на compression.ru
   
3. Ещё одна статья о деревьях принятия решений на Хабре
   
4. Toby Segaran, Programming Collective Intelligence (в данной книге есть глава посвящённая деревьям принятия решений, и вообще, если Вы ещё не читали этой книги — советую обязательно заглянуть туда 🙂
   
5. Такие библиотеки как Weka и Apache Mahout содержат реализацию деревьев принятия решений.
   

Деревья принятия решений

Деревья принятия решений

Простейшие деревья принятия решений хороши, пожалуй, только своей наглядностью. Они не оперируют вероятностями или весами. Для решения реальных задач часто используют усложнённые и дополненные модификации деревьев принятия решений.

Тем не менее, знакомство в деревьями принятия решений — это хороший первый шаг в машинном обучении. На их примере можно увидеть, какие бывают проблемы и подходы к решению этих проблем.

Задача деревьев принятия решений состоит в том, чтобы продлить булеву функцию, построенную по заданным точкам, на неизвестные точки.

Проще всего, оттолкнуться от примера.

Пример входных данных для построения дерева принятия решений

Пусть мы решаем задачу: мужчина перед нами или женщина. У нас есть несколько критериев:

• наличие юбки (S)
• длинные волосы (H)
• высокий голос (V)

Пусть у нас есть такие наблюдения:

S H V  sex
y y y  F
y y n  F
y n y  F
y n n  M
n y y  M
n n y  M

Это наши обучающие данные.

Построение дерева принятия решений (примитивный подход)

Дерево принятия решений состоит из

• узлов, в которых находятся атрибуты,
• рёбер, на которых находятся различные значения атрибутов,
• и листьев, которые содержат ответы.

Вы можете заглянуть в конец заметки и посмотреть на наше результирующее дерево.

Построение оптимального дерева принятия решений

В чём состоит оптимальность? Фактически, в том, чтобы первым же вопросом делать наибольший шаг к решению. То есть не начинать с несущественных вопросов. Оставить уточнения на потом.

Так мы, во-первых, можем придти к ответу быстрее (ответить на меньшее количество вопросов), и во-вторых, мы можем искусственно уменьшить дерево, чтобы избежать переобученности, и при этом дерево останется максимально точным и информативным.

Чтобы построить оптимальное дерево, мы должны оттолкнуться именно от информативности, нам понадобится энтропия.

Определение энтропии

Формально, можно дать такое определение: Пусть у нас есть множество из N элементов. Есть некое свойство S, которое может принимать два значения (значений может быть сколько угодно, но мы не будем здесь сильно углубляться; рассмотрим простейший случай). M этих элементов обладают свойством S=’y’. Соответственно, оставшиеся N-M элементов обладают свойством S=’n’. Тогда энтропия нашего множества по отношению к свойству S выражается формулой:

H(S) = -Σpᵢlog₂(pᵢ) = -( m/n * log₂(m/n) + (m-n)/n * log₂((m-n)/n) )

Формула с вероятностями pᵢ — это как раз общая формула, для случая, когда S может принимать несколько значений.

Чаще всего, логарифм берётся двоичный, но, строго говоря, основание логарифма не имеет большого значения. Если вы используете основание 2, то смысл энтропии в том, сколько надо бит для хранения вашей информации. Но если вы используете натуральный логарифм, то вы получаете «сколько нужно разрядов в системе счисления с основанием e». Может звучать странно, но именно это основание обеспечивает максимальную «вместимость» системы счисления. Это, — совершенная система счисления. Хотя, это уже немного другая история.

Не очень понятно? Давайте рассмотрим пример. Пусть у нас есть буквы русского алфавита (33 штуки). Есть какая-то их последовательность, где каждая буква встречается с равной вероятностью (1/33). Выберем свойство S. Допустим, будем считать свойством S гласность буквы. Тогда наша последовательность букв принимает вид гласная-гласная-негласная-гласная… Энтропия этого потока (не потока букв, а потока свойства S) вычисляется по формуле:

H(S) = - ( 10/33*log₂(10/33) + 23/33*log₂(23/33) ) = 0.885…

Это и есть энтропия нашего потока по отношению к свойству S.

То есть на запись одной буквы (вернее её признака S), при таких статистических свойствах последовательности, нам надо минимум 0.885 бит.

Здесь уместен вопрос, а что делать, если буквы в последовательности встречаются не с равной вероятностью? Этот вопрос будет рассмотрен применительно к Бейсовским классификаторам.

В наших задачах, «свойство» — это искомое свойство, которое должно определять дерево. То есть — пол.

Следующее, что нам понадобится — оценка информационного вклада атрибута.

Информационный вклад атрибута

Пусть у нас есть атрибут Q, который (для простоты) принимает два значения.

Тогда информационный вклад (gain) этого атрибута выражается такой разностью энтропий:

G(Q) = H(S) - p₁H₁(S) - p₂H₂(S)

где p₁ — доля данных с первым значение Q, p₂ — со вторым значением Q. Hᵢ — энтропия, рассчитанная на данном подмножестве.

Теперь мы можем оценить информационный вклад разных свойств:

Свойство            вклад
--------            -----
юбка (S)            0.553
длинные волосы (H)  0.057
высокий голос (V)   0

То есть, для ответа на наш вопрос (определение пола) больше всего информации даёт наличие юбки. С этого параметра и надо начинать систематизацию.

Кстати, обратите внимание, что голос не дал нам никакой новой информации. Действительно: с высоким голосом мы имеем двое мужчин и двое женщин, и с низким голосом одного мужчину и одну женщину. На основе этого параметра ничего сказать невозможно. (Пока.)

Начнём строительство дерева именно с признака «юбка». Мы получаем две подзадачи: построить два дерева для тех кто в юбке и тех, кто — нет.

Подзадача «есть»

Здесь у нас остаются только четыре обучающих случая:

S H V  sex
y y y  F
y y n  F
y n y  F
y n n  M

Даже просто глядя на эту табличку становится ясно, что оба параметра одинаково информативны (gain = 0.216). Действительно, вклад от y-случая и от n-случая одинаков. Посмотрите и посчитайте варианты.

То есть, нам всё равно, какой из атрибутов выбрать, давайте выберем «волосы».

Теперь мы получаем снова пару совсем простых подзадач:

S=y, H=y     S=y, H=n
----------   ----------
S H V  sex   S H V  sex
y y y  F     y n y  F
y y n  F     y n n  M

Тут уже всё однозначно: в H=y-случае мы можем только сказать — «женщина», а в случае H=n осталось проанализировать V (в этом контексте он уже может дать информацию).

Подзадача «нет»

Тут тоже осталось сделать одно действие:

S H V  sex
n y y  M
n n y  M

Тут видно, что ни V, ни даже H, не дают никакой информации.

Результирующее дерево принятия решений

           есть ли юбка?
           -+---------+-
            |         |
 .--  нет --'         `-- есть --.
 |                               v
 v                         длинные ли волосы?
 мужчина                   --+------------+--
                             |            |
                   .-- нет --'            да
                   |                      |
                   v                      v
            высокий ли голос?          женщина
            --+-----------+--
              |           |
    .-- нет --'           да
    |                     |
    v                     v
 мужчина               женщина

Видно, что так как мы располагали не полной информацией, то и некоторые ветки получились очень короткими. Но на самом деле, это не так уж плохо. На много хуже, если дерево переобучается. То есть, фактически, зазубривает большое количество ответов и начинает хорошо отвечать только на знакомые вопросы.

Что осталось за скобками

Мы тут только вскользь упомянули явление переобученности. Оно начинает играть очень большую роль, если данные зашумлены, а параметров много. Дерево начинает разрастаться, причём, длинные ветки становятся бесполезными.

То есть, дерево становится «занудой»: оно задаёт очень много вопросов, но качество ответов от этого не увеличивается.

Вкратце, чтобы этого избежать, дерево не простраивают до конца. Критерии остановки могут быть разными, но все они сводятся к тому, что если вы видите, что информации в этой ветке осталось не много, то пора прекращать её наращивать.

Второй вопрос, что делать, если обучающие патерны противоречивы? Например, у нас было два человека с одинаковым набором наших атрибутов, но одни — мужчина, а другой — женщина. В этом случае в ответе будет фигурировать или вероятность или (и это не редко) берётся просто ответ, правильно описывающий большее количество обучающих патернов.

И мы ничего не сказали о вероятностях. Решающие деревья с ними и не оперируют. Я постараюсь раскрыть этот вопрос отдельно.

Кроме того, когда вы начнёте сами делать решающие деревья, вы столкнётесь с рядом чисто практических проблем. Скажем, в наших данных могли быть не только одежда/волосы/голос, но и «рост в миллиметрах». Этот последний параметр оказался бы самым информативным (с точки зрения информационного вклада), но понятно, что на самом деле, он бесполезен.

Чтобы избежать таких проблем используется gain ratio, которое учитывает ещё и количество информации, требуемое для разделения по данному атрибуту. Используется так же индекс Гини. Про это же, возможно, расскажу отдельно.

---

---

Отправить

Как сделать правильный выбор используя метод дерева решений

Любое принятое человеком решение в условиях риска может иметь негативные последствия для финансового состояния предприятия. Чтобы этого не произошло, для прогнозирования результата рекомендуется применять метод дерева решений. Этот способ позволяет справиться практически с любой сложной задачей выбора таким образом, что выгода от совершенных действий будет максимальной.

Что такое дерево решений

Одной из самых эффективных математических моделей, в которой учитываются все факторы, влияющие на ситуацию, и выявляются закономерности между определенными явлениями, считается дерево решений. Поскольку усложнение социальных и экономических связей приводит к росту необоснованных решений, использование такого метода, позволяющего проанализировать состояние дел на текущий момент, является одним из самых лучших и выгодных вариантов выхода из сомнительной ситуации.

Основными элементами дерева принятия решений служат узлы событий, решений и исходов, которые соединяются между собой дугами. При создании модели на входе используются несколько переменных. Дерево строится таким образом, чтобы на основе входных данных, наиболее точно предсказать значение целевой переменной. Такой способ достаточно часто применяется для интеллектуального анализа данных в различных областях.

Все задачи, которые могут быть решены с использованием такой модели делятся на три типа:

1. Классификация. В результате применения метода выявляется принадлежность объектов к одному из нескольких классов, известных заранее.
2. Описание данных. Дерево решений позволяет выделить основную информацию об объектах и представить ее в наиболее компактном виде.
3. Регрессия. В случае, если значения целевой переменной непрерывные, дерево позволяет определить ее зависимость от входных данных. Характерными примерами деревьев решений такого типа считаются задачи численного прогнозирования, в которых с высокой точностью предсказывается значение целевой переменной.

Особенности построения дерева принятия решений и его анализ

Для решения серьезных стратегических задач используется специальное программное обеспечение, позволяющее построить дерево решений онлайн. При построении дерева решений вручную важно знать, что оно составляется сверху вниз. Первым шагом является выбор атрибута, который будет находится в корне дерева. При этом важно, чтобы он максимально подходил для классифицирования набора данных. Далее для каждого выбранного значения атрибута создается отдельная ветка. Последующее разделение данных происходит с учетом значения в указанной ветке. Аналогично процесс повторяется для каждой из имеющихся веток.

Основная трудность при построении дерева заключается в правильном выборе атрибута. Смысл метода заключается в том, чтобы во всех узлах (листьях) дерева находились наборы данных, минимально отличающихся друг от друга по классам (например, к классу Яблоко должно принадлежать преимущественное большинство объектов в наборе).

Построение дерева принятия решения производится с учетом следующих характеристик графической модели:

• наличие вершин событий, имеющих форму окружности;
• присутствие вершин конечных решений, называющихся листьями, которые изображаются в виде прямоугольников, окрашенных в цвет, отличный от всех вершин альтернативных решений;
• вилкой решений называют вершину альтернативных решений и все дуги, выходящие из нее;
• стохастической вилкой, отличающейся вероятностным характером, называют вершину событий и дуги, которые от нее отходят;
• для каждой из дуг вилки решений предусмотрены весы, которые отражают результат (убытки или приобретения) в случае реализации соответствующего решения;
• ко всем дугам стохастической вилки добавляют весы, характеризующие вероятность и степень выгоды данного события.

Чтобы проанализировать результаты, полученные путем составления дерева решений, необходимо совершить следующую последовательность действий:

1. Осуществить переход от атрибута к листу, значение в котором соответствует лучшему приобретению. При этом вероятность событий до принятия решения не учитывается.
2. Произвести оценку вероятности событий, предшествующих выбранному листу. При расчете всех приобретений, находящиеся на вершинах конечных решений, принимается во внимание соответствующая вероятность событий.

Чем граф отличается от дерева?

Графом называют множество вершин, попарно соединенных линиями, которые могут быть не только прямыми. Важной характеристикой графа является наличие связи между вершинами. От того, каким способом соединены два элемента, не зависит общая структура графа.

Часто при решении сложных задач возникает вопрос, чем граф отличается от дерева принятия решений. Разница заключается в том, что в этом алгоритме имеется логическая увязка метода декомпозиции поставленной задачи с синтезом наиболее подходящего варианта выбора.

Существует несколько типов математических моделей, построение которых осуществляется в виде графа:

1. Вершины обозначают физические объекты, ребра в графе связывают вершины друг с другом.
2. Вершины характеризуют как физические, так и нефизические объекты, связь ребер с вершинами зависит от функциональных и структурных особенностей последних.
3. Вершины – это нефизические либо физические объекты, которые могут находится в разных состояниях. Ребра отражают особенности причинно-следственной связи между вершинами графа.

Чтобы модель, построенная в виде графа, оказалась максимально эффективной, при ее создании рекомендуется соблюдать 2 условия:

• в вершинах графа должны отображаться самые важные состояния моделируемой системы;
• для обозначения отношений между вершинами должны быть выбраны важнейшие характеристики.

Основные типы моделей в виде графа

На практике используется множество математических моделей в виде графа, самыми распространенными являются следующие виды:

• блок-схема программного продукта, где вершинами служат команды, а ребра обозначают переходы между ними;
• системный граф, в котором вершины – это основные компоненты системы, а ребра – их взаимодействия;
• вычислительная сеть, где вершинами обозначаются основные компьютерные узлы, а ребрами – все линии связи;
• граф конфликтов, где в вершинах отражаются состояния рассматриваемой системы, а ребра указывают на конфликты между ними;
• граф транспортной сети, вершинами в котором являются разные города, а ребрами – дороги их связывающие.

Что такое дерево игры?

Одним из методов решения задач любой сложности в теории игр является дерево игры, которое имеет много схожих параметров с деревом принятия решений. Такая модель позволяет через определенные действия выразить все особенности столкновения интересов, характерные для салонных игр. Поскольку последовательность ходов во всех салонных играх устанавливается правилами, у игрока появляется большое количество альтернатив при каждом ходе.  

Победы в игре можно добиться только при условии, что на всех этапах будут учитываться все возможные ходы, а также те, которые за ними последуют. Исходя из этого следует, что абсолютно все ходы в игре взаимосвязаны. Дерево игры используется для формирования отвлечённого представления обо всех игровых ходах, а также наглядно показывает, какие выборы стали решающими и привели к результату.

Множество примеров дерева решений можно увидеть в повседневной жизни, причем проблема выбора может быть связана не только с серьезными жизненными решениями, но я самыми обыденными бытовыми нуждами. Благодаря продуманному алгоритму можно в любой ситуации структурировать имеющиеся данные и спрогнозировать исход событий.

Загрузка…

Древо решений — Decision tree

Традиционно, деревья решений были созданы вручную.

Дерево решений является поддержка принятия решений инструмент , который использует древовидную модель решений и их возможных последствий, в том числе случайных исходов событий, затрат ресурсов и полезности . Это один из способов , чтобы отобразить алгоритм , который содержит только условные операторы управления.

Деревья решений обычно используются в исследовании операций , в частности , в анализе решений , чтобы помочь определить стратегию , скорее всего , для достижения цели , но и популярным инструментом в области машинного обучения .

обзор

Дерево решений является блок — схемой , -как структура , в которой каждый внутренний узел представляет собой «тест» на атрибут (например , идет ли монета флип вверх головы или хвосты), каждая ветвь представляет собой результат теста, и каждый узел представляет собой лист класс этикетка (решение , принятое после вычисления всех атрибутов). Пути от корня до листа представляют собой правила классификации.

В анализе решений , дерево решений и тесно связано влияние диаграмма , используются в качестве визуального и аналитического инструмента поддержки принятия решений, где ожидаемые значения (или ожидаемой полезности ) конкурирующих альтернатив рассчитываются.

Дерево решений состоит из трех типов узлов:

1. Решение узлов — как правило, представлены квадратами
2. Chance узлы — как правило, представлены кружками
3. Конечные узлы — как правило, представлены треугольниками

Деревья решений обычно используются в исследовании операций и операций управления . Если на практике решение должно быть принято онлайн, без вызова при неполном знании, дерево решений должно быть параллельно с вероятностной моделью как лучшая моделью выбора или модель выбора онлайн — алгоритмом . Другое использование дерев решений является как описательным средством для вычисления условных вероятностей .

Деревья решений, влияние схемы , сервисные функции , а также другие аналитические решения инструменты и методы учат студентов в школах бизнеса, экономики здравоохранения и общественного здоровья, а также примеры исследования операций и управления научными методами.

Схема принятия решений строительных блоков

Элементы дерева принятия решений

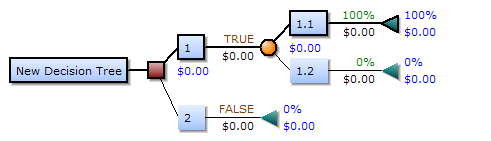
Нарисованные слева направо, дерево решений только лопнуть узлов (расщепление путей), но нет погружения узлов (сходящихся путей). Таким образом, используется вручную, они могут расти очень большой и затем часто трудно полностью рисовать от руки. Традиционно, деревья решений были созданы вручную — как в сторону пример показывает, — хотя все больше и больше, специализированное программное обеспечение используется.

правила принятия решений

Дерева решений могут быть линеаризованы в правила принятия решений , где результат является содержимым узла листа, а также условия вдоль пути образуют конъюнкции в пункте если. В целом правила имеют вид:

если condition1 и condition2 и condition3 затем результат.

Правила принятия решений могут быть получены путем построения ассоциативных правил с целевым переменным справа. Они также могут обозначать временные или причинно — следственные связи.

Схема принятия решений с использованием блок-схемы символов

Обычно дерево решений обращается с использованием блок — схемы символов , как это проще для многих , чтобы прочитать и понять.

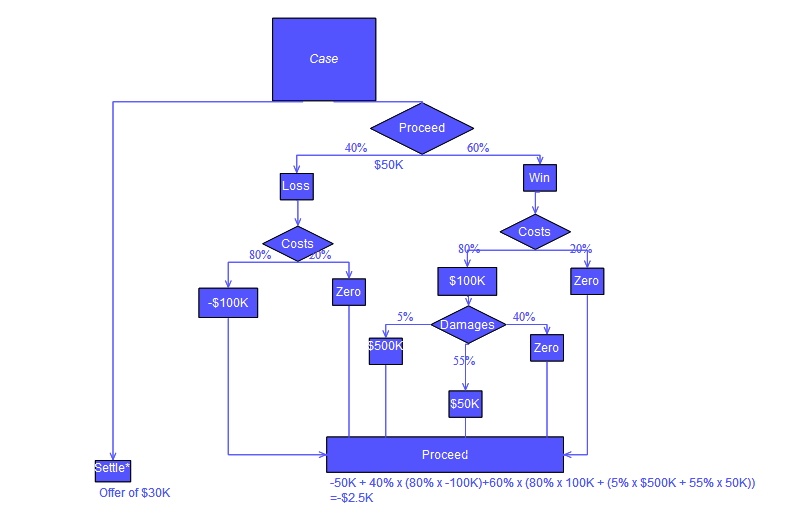
пример анализа

Анализ может принять во внимание , принимающее решение (например, компании) предпочтение или функции полезности , например:

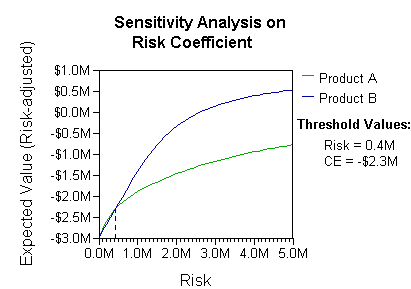
Основное толкование в этой ситуации является то, что компания предпочитает риск и выигрыши в реальных предпочтениях риски коэффициентов Б (больше, чем $ 400K в этом диапазоне неприятия риска, компания должна будет моделировать третью стратегию, «Ни А, ни Б») ,

Другой пример, который обычно используется в операциях исследовательских курсов, является распределением спасателей на пляжах (он же «Жизнь это пляж» , например). Пример описывает два пляжа с спасателями , которые будут распределены на каждом пляже. Существует максимальный бюджет B , которые могут быть распределены между двумя пляжами (в общей сложности), и с помощью таблицы предельного дохода, аналитики могут решить , сколько спасателя выделить каждый пляж.

Спасателей на каждом пляже	Утопление предотвращены в целом, пляж # 1	Утопление предотвращены в целом, пляж # 2
1	1	3
2	4	0

В этом примере, дерево решений можно сделать , чтобы проиллюстрировать принципы убывающих на пляж # 2.

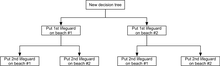Пляж Дерево принятия решений

Дерево решений показывает, что, когда последовательно распределяя спасатель, поставив первый спасатель на пляже # 1 будет оптимальным, если есть только бюджет на 1 спасатель. Но если есть бюджет на два охранников, а затем размещение как на пляж # 2 предотвратил бы больше общего утопление.

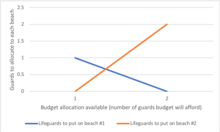
диаграмма Влияние

Большая часть информации в дереве решений можно представить в более компактной форме, как влияние диаграмма , сосредоточив внимание на вопросах и отношениях между событиями.

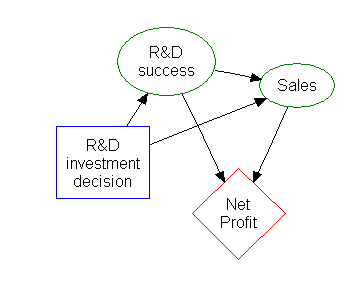
Прямоугольник слева представляет собой решение, овалы представляют собой действие, и алмаз представляет результаты.

индукционная правило Ассоциация

Деревья решений также можно рассматривать в качестве порождающей модели индукционных правил из эмпирических данных. Оптимальное решение дерево затем определяется как дерево, которое составляет большую часть данных, минимизируя при этом количество уровней (или «вопросы»). Некоторые алгоритмы, чтобы генерировать такие оптимальные дерева были разработаны, например, ID3 / 4/5, CLS, помощник и CART.

Преимущества и недостатки

Среди инструментов поддержки принятия решений, дерева решений (и влияние диаграмма ) имеют ряд преимуществ. Деревья решений:

• Просты для понимания и интерпретации. Люди могут понять модели дерева решений после краткого объяснения.
• Иметь значение, даже с небольшими твердыми данными. Важные идеи могут быть сформированы на основе экспертов, описывающих ситуацию (его альтернативы, вероятность и затраты) и их предпочтения в отношении результатов.
• Помогите определить худшие, лучшие и ожидаемые значения для различных сценариев.
• Используйте белую коробку модель. Если данный результат обеспечивается моделью.
• Может сочетаться с другими методами решения.

Недостатки деревьев решений:

• Они неустойчивы, а это означает, что небольшое изменение данных может привести к большим изменениям в структуре оптимального дерева решений.
• Они часто являются относительно неточными. Многие другие предсказатели работать лучше с аналогичными данными. Это может быть исправлено путем замены одного дерева решений с случайным лесом дерев решений, но случайный лес не так легко интерпретировать как единое дерево решений.
• Для данных , включая категориальные переменные с разным числом уровней, усиление информации в процессе принятия дерев смещено в пользу этих атрибутов с большим количеством уровней.
• Расчеты могут быть очень сложными, особенно если много значений являются неопределенными и / или, если многие результаты связаны между собой.

Смотрите также

Рекомендации

внешняя ссылка

Монте-Карло

Надстройка MS Excel «Дерево решений» предназначена для построения и анализа древа решений и событий для ситуаций неопределенности и риска.

Древо решений и событий строится в обычном листе Excel. При построении автоматически добавляются стандартные формулы для выбора, оценки среднеожидаемого результата и расчета вероятности.

Основная версия надстройки работает в 32-bit и 64-bit версиях MS Excel начиная с MS Office 2007. Более старые версии MS Excel не поддерживаются.

Рабочий лист с построенным деревом решений форматируется специальным образом, но остается обычным листом Excel и после построения дерева может свободно редактироваться.

Файл надстройки имеет название: «Decision Tree  уу. mm. xlam» (в зависимости от версии) и может либо запускаться как обычный файл MS Excel (при этом нужно согласиться с запуском макросов надстройки), либо подключаться автоматически как любая надстройка (для этого нужно записать файл в папку надстроек MS Excel C:\Users\_{Пользователь}\AppData\Roaming\Microsoft\AddIns\). После запуска появляется новый пункт в меню Excel «Дерево решений».

Для принятия решений в ситуации неопределенности широко используется метод «таблиц выигрышей и потерь». Однако в сложных случаях приходится выбирать между альтернативами, каждая из которых представляет собой «многошаговый» процесс принятия решений. Такие шаги могут быть разнесены во времени, на каждом шаге может возникать новый набор альтернатив и сценариев будущего, усложняется расчет вероятностей различных событий.

В этом случае визуализировать процесс выбора из рассматриваемых альтернатив удобно с помощью схемы или графа, называемых деревом (древом) решений. Дерево решений — это необходимый инструмент при стратегическом планировании и инвестиционном анализе.

Краткая справка к надстройке

(смотрите актуальную версию справки в меню надстройки)

Начало работы.

Дерево решений строится с помощью команд интерфейсного окна надстройки. Это окно может быть закрыто и открыто снова для продолжения работы на любом этапе построения дерева решений.

Дерево решений должно иметь строго определенную структутру для того, чтобы автоматически генерируемые формулы работали правильно, и чтобы надстройка могла правильно определить строение дерева при внесении изменений в дерево решений.

Поэтому все изменения дерева, за исключением добавления численных данных и расчетных формул, нужно делать только через интерфейс надстройки (!!!).

1. Начинать построение дерева нужно кнопкой «Создать дерево», по нажатии которой будет создана новая страница со стандартным началом дерева («стволом»). Ствол (начало дерева) показан коричневой линией. Красная звездочка здесь и далее — возможная точка «роста» дерева, т. к. в ячейку, содержащую звездочку, можно вставить продолжение дерева. Часть ячеек скрыта, чтобы не отягощать схему служебной информации.

2. Чтобы продолжить конструирование дерева решений нужно определиться, из скольких вариантов действий придется выбирать главное решение. Число вариантов указывается в окне «Количество ветвей» с помощью стрелок больше\меньше справа от окна. Невозможные варианты числа ветвей блокированы. По умолчанию в панели «Добавить развилку» событий отмечен пункт «Выбор решения», означающий, что решение можно выбрать из определенного числа вариантов. Если оставить число ветвей равным 2 и нажать кнопку «Добавить дерево» прирастет развилкой зеленого цвета с комментарием Решение 1, 2…. В каждой из двух появившихся звездочек дерево может быть продолжено.

В корневой ячейке развилки автоматически записывается формула =МАКС(L2:L6), с помощью которой позднее будет сделан выбор, какое из решений наиболее привлекательно.

Иногда дерево может начинаться развилкой «Варианты будущего». В этом случае решение выбрать нельзя — тут с определенной вероятностью и независимо от вашей воли реализуется одно из возможных будущих. Но в подавляющем большинстве случаев развилкой «Варианты будущего» дерево в какой-то момент продолжается, что и реализует наше неполное знание о будущем.

Для того, чтобы вставить такую развилку нужно щелкнуть мышкой радиокнопку «Варианты будущего», выбрать число ветвей (допустим, 3), выделить (щелкнуть мышкой) одну из ячеек со звездочкой и нажать кнопку «Добавить». В результате к дереву решений добавится развилка оранжевого цвета с тремя ветками и дополнительной информацией о вероятности каждой ветви.

Автоматически сгенерированная формула =СУММПРОИЗВ(N2:N4;Q2:Q4) позволяет оценить средневзвешенный результат для этой вероятностной развилки событий.

Манипуляции с деревом решений.

1. Команды Undo и Redo. Две кнопки со стрелками в панели «Операции» в левом нижнем углу окна интерфейса служат для отката последних изменений или возврата к более новой версии дерева. Следует иметь ввиду, что встроенный в MS Excel механизм Undo\Redo не поддерживает изменения, которые делают надстройки. Поэтому при работе надстройки возникают два независимых набора последних изменений: версия Excel и версия надстройки «Дерево решений». Если требуется откатить назад изменения, сделанные вне интерфейса надстройки, следует пользоваться меню Правка — Отменить\Повторить. Состояние дерева решений после каждой операции через интерфейс надстройки так же запоминается и может быть возвращено. Однако при этом будут потеряны изменения, сделанные вне интерфейса после последней операции. К сожалению, это может запутать пользователя при возврате больше чем на один-два шага.

После закрытия окна интерфейса история операций уничтожается, даже если сам файл остается открытым.

2. Команда «Удалить» панели «Продолжение дерева от узла». С помощью этой кнопки можно удалить все продолжение дерева со всеми разветвлениями начиная от выделенного узла. Если выделена ячейка, не являющаяся узлом дерева, никакой реакции не последует.

3. Команды «Копировать» и «Вставить» панели «Продолжение дерева от узла». Если выделить ячейку с узлом дерева и нажать кнопку «Копировать», все продолжение дерева от заданного узла и до конца ветвей скопируется в специальный буфер. Скопированное продолжение дерева решений можно вставить в любую ячейку со звездочкой. Это удобно, когда часть дерева нужно повторить в другом месте. Копия сохраняется до тех пор, пока не последует другая команда «Копировать».

4. Команда «Выровнять» панели «Дерево».

Если дерево решений построено, но концы ветвей оказываются в разных столбцах бывает удобно выровнять их для лучшего представления дерева.

Для этого можно использовать команду «Выровнять». При нажатии этой кнопки все открытые ветви дерева доращиваются до самой длинной ветки путем добавлений одиночных веток, повторяющих предшествующую информацию.

Такую одиночную ветку можно вставить и добавляя «развилку».

5. С помощью операции «Добавить» панели «Добавить развилку событий» можно вставить дополнительную развилку в существующий узел дерева решений, если в результате анализа дерева нужно, скажем, предоставить дополнительную возможность выбора. Для этого следует выделить узел дерева (например, L2), задать тип узла и количество ветвей и нажать кнопку «Добавить». Старое продолжение дерева решений от текущего узла будет перенесено в конец первой ветки вновь вставленного узла Q2.

Переменные и вычисления.

Для расчетов по дереву решений используются данные, отражаемые в дереве под именем «Переменные». По умолчанию (по соображениям техники программирования) в дереве используется одна переменная (столбец озаглавлен «_1»).

1. Число переменных можно изменить с помощью панели «Переменные».

Если установить с помощью стрелки вверх у окна числа переменных величину 3 и нажать расположенную тут же кнопку «Добавить», число переменных увеличится на 3 (не забудьте отметить кнопку «Показать», иначе никаких изменений не увидите).

Если нужно уменьшить количество переменных, следует стрелкой вниз выбрать отрицательное число, показывающее, сколько переменных нужно ликвидировать. При этом надпись на кнопке измениться на «Удалить». Так как меньше одной переменной оставить нельзя, при выборе невозможного уменьшения окно подсвечивается розовым, а кнопка «Добавить\Удалить» деактивируется.

Изменить количество переменных можно на любой стадии работы с деревом решений.

2. После завершения ввода данных или на этапе построения дерева бывает удобно видеть дерево в возможно более компактном виде. Для этого используют команду «Скрыть» переменные. При этом к столбцам, содержащим переменные, применяется команда Excel «Скрыть столбцы». Кнопка «Показать» возвращает столбцам с переменными видимость.

3. При вводе значений переменных достаточно записать их в той развилке, после которой значения переменных становятся определенными. В более поздних развилках введенные значения переменных будут воспроизведены автоматически, так как ячейки переменных содержат формулы-ссылки на предшествующую ветвь.

4. В завершенном дереве решений все оконечные звездочки всех веток должны быть заменены на численные значения или формулы, рассчитывающие эти значения по переменным. Это — плоды (иногда нелогично говорят — листья) дерева, т.е. численные (финансовые) характеристики ситуаций, к которым привели описанные в дереве цепочки событий.

 

Замечание. В узлах «Выбор решения» записана формула =МАКС(….), выбирающая наибольшее значение в следующих узлах данной развилки. Очевидно, это правильно только если чем больше, тем лучше. Если лучшим является минимальное значение, следует заменить формулы =МАКС(….) на =МИН(….) (это можно сделать и через меню «Правка\Заменить»).