Расход жидкости при истечении через отверстие — МегаЛекции
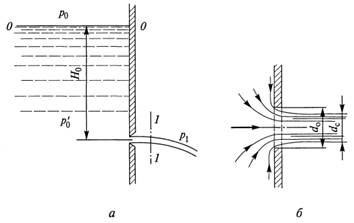
При работе с жидкостью возникает необходимость расчета истечения жидкости из отверстий и щелей, предусмотренных конструкцией аппарата или появившихся при аварии. Для анализа такого течения рассмотрим истечение жидкости из резервуара через малое круглое отверстие, в тонкой стенке в атмосферу или в пространство, заполненное газом или той же жидкостью. Пусть отверстие расположено на достаточно большой глубине Н под уровнем свободной поверхности жидкости и через него жидкость вытекает в воздушное пространство (рис. 1.12, а).
Это классическая задача, которую исследовал еще Ньютон. В этом течении потенциальная энергия жидкости в поле тяготения Земли превращается в кинетическую энергию струи жидкости. Нас интересует величина скорости, которую достигает жидкость и ее объемный расход. Пусть отверстие имеет острую кромку с внутренней стороны. Частицы жидкости втекают в отверстие по плавным траекториям из всего объема резервуара. Никакая линия тока не имеет нулевого радиуса кривизны, потому что жидкость обладает инерционной массой и для очень малого радиуса поворота необходим очень большой перепад давления. Крайние линии тока отрываются от стенок и струя несколько сжимается, получив площадь сечения S
V=φ(2gH)1
где 
— коэффициент скорости, φ=0,97 ч-0,98. Объемный расход жидкости, вытекающей из отверстия,
Q = μS0(2gH)1‘2,
где ц — коэффициент расхода, который в широком диапазоне значений числа Рейнольдса можно считать равным μ=0,62: μ=φε
Такая же закономерность получается для отверстия, расположенного на боковой вертикальной стенке сосуда (см. рис. 1.12, б). Здесь под величиной Н следует понимать расстояние от свободной поверхности до центра тяжести площади сечения малого отверстия.
В случае больших отверстий, вертикальный размер сечения которых сравним с высотой Н, уже нельзя считать, что напор H остается постоянным для всех точек сечения. Рассмотрим случай прямоугольного отверстия шириной сечения Ь и высотой H, меняющейся от значения h2 до Нг. Элементарный слой жидкости с высотой dh, находящийся ниже свободной поверхности на величину h, будет иметь объемный расход
dQ=μb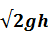 
dh
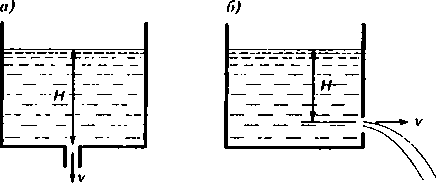
рис 1.12
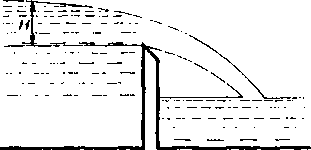Рис. 1.13. Схема течения воды через не затопленный водослив с тонкой стенкой
|
2g [h33‘2-h23‘2].Если струя жидкости переливается через вырез в стенке, расположенной перпендикулярно потоку, то такое течение называется водосливом. Одним из наиболее простых является водослив с тонкой стенкой, приведенный на рис. 1.13.
Высота превышения поверхности воды верхней кромки стенки, обозначенная на рис. 1.13 через H, называется статическим напором водослива. Ширину водослива, измеряемую в направлении, перпендикулярном плоскости рисунка, обозначим через Ь. Нижним бьефом называется часть потока, расположенная ниже стенки по течению.
Будем рассматривать водослив с тонкой стенкой, в котором уровень жидкости в нижнем бьефе расположен ниже ребра стенки. Такой водослив называется незатопленным.
Основной величиной, интересующей инженера, является объемный расход жидкости через водослив. Он определяется по теории истечения жидкости из отверстия, если в последней формуле для прямоугольного отверстия положить h2 = 0, H
Q = (2/3)μb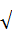 
2gH3‘2.
Обозначая через т величину (2/3)д, получим основную зависимость теории водосливов
Q=mb(2g)ll2H312,
где т — коэффициент расхода водослива. Эксперименты дают значения т в пределах 0,42 — 0,50 для течений воды в водосливе метровых размеров.
4 Гидравлический удар в трубопроводах
Называя жидкость несжимаемой или капельной, мы обычно имеем в виду малую ее сжимаемость сравнительно с газами, при изменении давления на 0,1 МПа объем жидкости изменяется всею на сотые доли процента. Есть однако процессы, при которых или изменения объема существенны и ими нельзя пренебрегать. К их числу относится большая группа динамических процессов, связан с распространением волн давления в трубопроводах, в частности, явление гидравлического удара. Гидравлический удар (гидроудар) в трубопроводе – это мгновенный скачок давления воды в водонапорных трубах, связанный с резким изменением скорости движения потока воды. В зависимости от направления скачка давления гидроудар разделяют на:
1 Положительное давление в трубопроводе возрастает из-за резкого перекрытия трубы или включения насоса;
Для систем водоснабжения и отопления опасен первый вариант. Слишком большой скачок давления может повредить водопроводные трубы, вызывая продольные трещины и раскол, нарушить герметичность запорной арматуры, вывести из строя водопроводное оборудование (насосы, теплообменники). Поэтому гидравлический удар нужно предотвращать и/или уменьшать его силу.
Причина гидроудара
В автономной системе водоснабжения загородного дома, когда давление в водопроводе создаётся, например, скважинным насосом, гидроудар возникает при резком прекращении потребления воды, когда перекрывается кран. Поток воды, который двигался к трубопроводу, не может мгновенно остановиться и по инерции «ударяется» в образовавшийся при закрытии крана водопроводный «тупик». Реле давление в этом случае не спасает от гидроудара, а только реагирует на него, отключая насос уже после того, как кран перекрыт и давление превысило максимальное значение. Выключение насоса тоже не происходит мгновенно, так же как и остановка потока воды в трубопроводе.
Защита от гидроудара
Сила гидроудара зависит от скорости потока воды в трубе до и после перекрытия трубы: чем выше скорость потока, тем сильнее будет удар при его резкой остановке. В свою очередь сама скорость потока зависит от диаметра трубопровода: чем больше диаметр трубы, тем ниже скорость потока воды в ней при одинаковом расходе воды. Таким образом, использование труб большего диаметра ослабляет гидроудар.
Второй способ ослабить силу гидравлического удара – это увеличить время перекрытия трубопровода (или включения насоса). Для постепенного перекрытия трубы можно использовать запорные краны вентильного типа.
Для насосов есть комплекты плавного пуска, которые не только позволяют избежать гидроударов при включении, но и продлевают срок службы самого насоса.
Наконец, третий способ защиты от гидроудара – это использование демпферного устройства – мембранного расширительного бака, который будет «гасить» скачки давления.
ЗАКЛЮЧЕНИЕ
Данная мне тема является очень актуальной при проектировании водоснабжения и водоотведения жилых и промышленных зданий и сооружений, правильного подбора сечений труб и отводов а так же защиту от гидравлического удара.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Истечние жидкости из отверстий, насадков и из-под затворов
5.4. Истечение через насадки при постоянном напоре
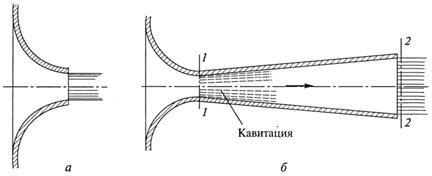
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.
Первый режим — безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рис.5.7).
Рис. 5.7. Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле:
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и преобразовать его, то можно получить падение давления внутри насадка
P2 — P1 0,75HgρПри некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому
Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого режима ко второму (рис.5.8).
Рис. 5.8. Второй режим истечения через насадок
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме — большое сопротивление и недостаточно высокий коэффициент расхода, а на втором — очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих коэффициентов.
Рис. 5.9. Истечение жидкости через насадки а — расширяющиеся конические; б — сужающиеся конические; в — коноидальные; г — внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
5.5. Истечения через отверстия и насадки при переменном напоре (опорожнение сосудов)
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
Рис. 5.10. Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:
где dh — изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
Истечение жидкости через отверстие » СтудИзба
4 ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
4.1 Истечение через отверстие в тонкой стенке
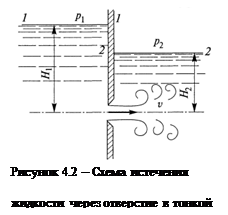
Рассмотрим истечение жидкости через отверстие диаметром d0 в стенке бака, расположенное на глубине Н0, в газовую среду с некоторым давлением р1 (рисунок 4.1, a). При этом предполагается, что если отверстие мало по сравнению с размерами бака и глубиной Н0, то другие стенки бака и свободная поверхность жидкости не влияют на приток жидкости к отверстию.
Характер истечения в этом случае показан на рисунке 4.1, б. Частицы жидкости приближаются к отверстию из всего близлежащего объема, двигаясь по различным траекториям. Некоторые из них при попадании в отверстие должны изменить направление своего движения на 90°. Так как каждая частица имеет массу, то мгновенно изменить направление своего движения она не может. Следствием этого является сжатие струи жидкости при истечении. Процесс сжатия струи практически завершается на расстоянии, равном примерно одному диаметру отверстия, и после этого струя приобретает цилиндрическую форму с диаметром поперечного сечения dc. Точно такими же будут условия истечения, если отверстие выполнено в толстой стенке со снятием фаски с внешней стороны.
|
Степень сжатия струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия
. (4.1)
Определим расход Q жидкости через рассматриваемое отверстие. Для этого запишем уравнение Бернулли для двух сечений (см. рисунок 4.1, а): сечения 0-0 и сечения 1-1. Сечение 0-0 — это открытая поверхность жидкости в баке, следовательно, в нем давление р0, а скорость жидкости можно считать равной нулю. Сечение 1-1 струи должно быть выбрано в той ее части, где струя уже приняла цилиндрическую форму; тогда в этом сечении давление равно давлению р1 окружающей среды. Если в качестве плоскости сравнения выбрать горизонтальную плоскость, проходящую через ось отверстия, то получим
,
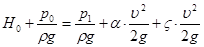где α — коэффициент Кориолиса, учитывающий неравномерность распределения скорости по сечению 1—1 струи;
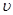— средняя скорость жидкости в сечении 1—1;
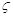— коэффициент сопротивления отверстия, учитывающий торможение частиц жидкости о входную кромку отверстия.
Перенесем первое слагаемое правой части уравнения в левую часть и обозначим ее как расчетный напор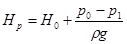 
, тогда
;
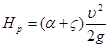отсюда средняя скорость истечения жидкости
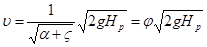, (4.2)
где 
— безразмерная величина, получившая название коэффициент скорости и определяемая по формуле
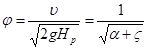. (4.3)
В случае истечения идеальной жидкости (α = 1 и 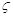= 0) из формулы (4.3) следует, что = 1, т.е. скорость истечения идеальной жидкости
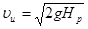. (4.4)
Таким образом, на основании сравнения формул (4.3) и (4.4) можно сформулировать физический смысл коэффициента скорости . Это величина, равная отношению средней скорости истечения реальной жидкости к скорости истечения идеальной жидкости в тех же условиях. Очевидно, что при истечении реальной жидкости коэффициент всегда меньше единицы.
Расход Q при истечении определим как произведение средней скорости истечения реальной жидкости и фактической площади живого сечения струи. Используя формулы (4.1) и (4.3), получим
.
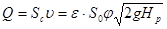Произведение двух безразмерных коэффициентов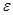 
и принято называть коэффициентом расхода и обозначать
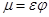. (4.5)
Тогда
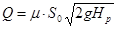. (4.6)
Из (4.6) следует, что
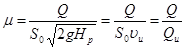
Таким образом, физический смысл коэффициента расхода 
состоит в том, что он численно равен отношению действительного расхода Q при истечении жидкости к тому расходу Qu, который имел бы место при отсутствии сжатия струи и сопротивления истечению.
Следует обратить внимание на то, что Qu не является расходом при истечении идеальной жидкости, так как идеальная жидкость отличается от реальной только отсутствием вязкости. Эффект же сжатия струи при истечении идеальной жидкости, связанный с инерционными свойствами частиц жидкости, в условиях отсутствия трения проявляется в еще большей степени.
На практике формула (4.6) используется достаточно редко из-за сложностей, возникающих при определении расчетного напора Hр, особенно в закрытых гидросистемах. Поэтому сделаем следующие преобразования. Обозначим внутри бака на уровне оси отверстия на некотором удалении от него (где скорость жидкости можно принять равной нулю) давление 
(см. рисунок 4.1, а), тогда перепад давления Δр, под действием которого происходит истечение жидкости через отверстие, запишется в виде
.
Выразив из этой формулы напор Hp и подставив его в формулу (4.6), получим
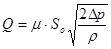. (4.7)
При помощи формулы (6.7) решается основная задача — определение расхода жидкости при истечении. Она широко применяется при расчетах элементов машиностроительных гидросистем.
Таким образом, нами введены в рассмотрение три коэффициента — 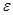, и , характеризующие процесс истечения жидкости. Все они являются функцией числа Рейнольдса Re. Однако для маловязких жидкостей (воды, бензина и др.), истечение которых, как правило, происходит при больших значениях Re, эти коэффициенты практически постоянны: 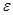= 0,64; = 0,97; = 0,62. При истечении минеральных масел через круглые отверстия в области квадратичного сопротивления можно принять = 0,65.
4.2 Истечение под уровень
При течении жидкости в закрытых руслах часто приходится иметь дело с истечением жидкости не в газовую среду, а в пространство, заполненное этой же жидкостью (рисунок 4.2). Такое истечение называется истечением под уровень или истечением через затопленное отверстие.
Здесь, так же как и в предыдущем случае, при определении расхода Q следует составить уравнение Бернулли. Запишем его для сечений 1-1 и 2-2, в которых скорости движения жидкости принимаются равными нулю:
,
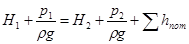где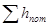 
— потери напора при движении жидкости между сечениями 1-1 и 2-2.
При определении потерь напора в этом случае необходимо учитывать, что они складываются из двух составляющих:
,
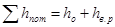где ho — потери напора на торможение частиц жидкости о входную кромку отверстия;
hв.р — потери напора на внезапное расширение в баке после прохождения жидкости через отверстие.
Потери ho практически равны потерям при истечении через отверстие в газовую среду:
.
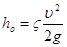Следует иметь в виду, что при истечении под уровень вся кинетическая энергия струи, приобретенная частицами жидкости в отверстии, при попадании в покоящуюся жидкость теряется на вихреобразование так же, как при внезапном расширении. Поэтому потери hв.р численно равны соответствующему скоростному напору, посчитанному по средней скорости жидкости в струе с учетом коэффициента Кориолиса α:
.
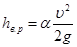Таким образом, суммарные потери напора
.
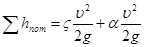Подставив полученное выражение в уравнение Бернулли, получим
.
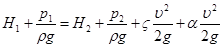Если в этом уравнении за расчетный напор принять выражение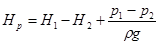 
, то после преобразований можно получить формулу, определяющую значение средней скорости жидкости в сжатом сечении струи:
,
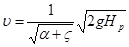которая совпадает с формулой (4.2). Это значит, что, проводя дальнейшие преобразования, необходимые для получения формулы, определяющей расход Q при истечении, можно получить формулы (4.6) и (4.7).
Таким образом, как при истечении в газовую среду, так и при истечении под уровень расчетные формулы, определяющие расход Q, имеют один и тот же вид. Кроме того, как показала практика, коэффициенты 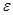, и , использующиеся в этих формулах, в обоих случаях истечения имеют одинаковые значения при равенстве соответствующих чисел Рейнольдса.
4.3 Истечение через насадки
Анализ полученных формул (4.6) и (4.7) позволяет заключить, что увеличение расхода Q при истечении через отверстие с неизменными So и Hр, возможно при увеличении коэффициента расхода . Решению этой задачи служат насадки различной конструкции. Различают следующие типы насадков: цилиндрические (внешний и внутренний), конические (сходящийся и расходящийся), коноидальные и комбинированные.
Внешним цилиндрическим насадком называется короткая трубка или сверление в толстой стенке без обработки входной кромки (рисунок 4.3). Его длина l = (3…5) d, где d — диаметр отверстия.
На практике при истечении в газовую среду можно наблюдать два режима истечения жидкости через цилиндрический насадок: безотрывный (см. рисунок 4.3, а) и с отрывом потока от стенок (см. рис. 4.3, б).
Безотрывный режим истечения характеризуется тем, что внутри насадка поток жидкости вначале сжимается до некоторого минимального поперечного сечения, площадь которого можно определить по значению коэффициента сжатия струи 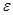, взятого для случая истечения жидкости через отверстие в тонкой стенке, а затем расширяется до размеров отверстия в насадке. В итоге при таком режиме истечения из насадка на его выходе сжатие струи отсутствует ( 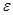= 1) и площадь сечения струи равна площади проходного сечения отверстия в насадке. Поэтому в данном случае при определении расхода Q по формуле (4.7) коэффициент расхода = .
Для этого случая при турбулентном режиме течения жидкости внутри насадка (α = 1) и коэффициенте потерь 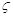= 0,5 (потери напора определяются как потери при внезапном сужении) коэффициент расхода
.
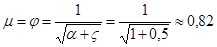Сравнение полученных коэффициентов скорости и расхода со значениями этих коэффициентов при истечении жидкости через отверстие в тонкой стенке ( = 0,97, = 0,62) показывает, что при безотрывном истечении через цилиндрический насадок расход Q получается больше, чем при истечении через такое же отверстие в тонкой стенке. Средняя скорость 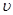жидкости в потоке на выходе из насадка при этом получается меньше. Уменьшение скорости вызвано большими потерями напора в насадке по сравнению с потерями, которые возникают на входной кромке отверстия в тонкой стенке.
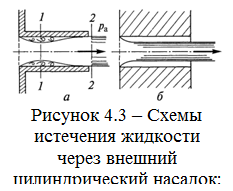Увеличение расхода Q при этом является следствием отсутствия сжатия струи на выходе из насадка. Кроме того, при безотрывном истечении на входе в насадок поток сжимается, а значит, в соответствии с законом Бернулли скорость движения жидкости увеличивается, а давление в этом месте уменьшается по сравнению с давлением среды, куда происходит истечение. Причем степень сжатия потока, а следовательно, и степень уменьшения давления в узком сечении потока тем больше, чем больше расчетный напор Hр. При этом на входной кромке отверстия создается больший перепад давления, чем при истечении жидкости через отверстие в тонкой стенке при одном и том же Hр. В результате этого обеспечиваются дополнительный приток жидкости из бака в насадок и увеличение расхода Q.
Со сжатием потока на входе в насадок, а также с зависимостью степени сжатия от расчетного напора Нр связано внезапное изменение режима истечения через насадок. Это происходит при определенном критическом расчетном напоре Hкр, который при истечении воды в атмосферу составляет около 14 м водяного столба. Внешне эта смена режима истечения заключается в том, что поток жидкости отрывается от стенок насадка и жидкость истекает в атмосферу, не касаясь их. Этот режим истечения получил название истечение с отрывом потока от стенок насадка (см. рисунок 4.3, б).
При истечении до отрыва потока от стенок давление в узком сечении потока приближается к давлению насыщенных паров. Как известно, в потоке при таком давлении следует ожидать возникновения кавитации. Однако кавитационный режим течения при истечении в газовую среду не успевает сформироваться. Возникающая начальная стадия кавитации способствует проникновению газовой среды внутрь насадка. Начиная с этого момента струя жидкости после сжатия теряет взаимодействие со стенками насадка и уже не расширяется, а перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится таким же, как и при истечении через отверстие в тонкой стенке (см. подраздел 4.1), с теми же значениями коэффициентов 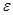, и . Таким образом, при смене режима истечения происходит скачкообразное уменьшение расхода приблизительно на 20 % за счет существенного сокращения площади сечения потока.
Следует также отметить, что если после отрыва потока от стенок напор Hр начать снижать, то режим истечения с отрывом сохраняется вплоть до самых малых значений напора, пока не произойдет самопроизвольное смачивание внутренней поверхности насадка. Это значит, что режим истечения с отрывом через цилиндрический насадок возможен и при Hр < Hкр. Следовательно, при Hр < Hкр возможны оба режима истечения.
Если жидкость истекает через цилиндрический насадок под уровень, то отрыва потока от стенок не происходит. Начиная с момента, когда в узком сечении потока внутри насадка давление становится близким к давлению насыщенных паров жидкости, на входе в насадок возникает кавитация и происходит связанное с ней увеличение сопротивления насадка.
Итак, использование внешнего цилиндрического насадка вместо отверстия в тонкой стенке обеспечивает в режиме безотрывного истечения при тех же значениях расчетного напора и поперечных размеров отверстия увеличение расхода через насадок.
Однако внешний цилиндрический насадок имеет и недостатки:
— в режиме безотрывного истечения — большое сопротивление и недостаточно высокий коэффициент расхода;
— в режиме истечения с отрывом — низкий коэффициент расхода;
— двойственность режима истечения в газовую среду при Hр < Hкр;
— возможность возникновения кавитации при истечении под уровень.
Это необходимо учитывать при использовании цилиндрического насадка в качестве жиклера, дросселя или форсунки. Улучшить внешний цилиндрический насадок можно за счет скругления входной кромки насадка. Для жиклеров рекомендуется снятие фаски на входе в отверстие с углом конусности около 60°.
Чем больше радиус закругления входной кромки насадка, тем ниже его коэффициент сопротивления и тем выше коэффициент расхода. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический насадок приближается к коноидальному насадку, или соплу.
|
Коноидалъный насадок (сопло) (рисунок 4.4, а) очерчивается по форме естественно сжимающейся струи, поэтому поток жидкости на выходе насадка получается безотрывным, параллельно-струйным и устойчивым к возникновению кавитации. Для этого насадка коэффициент сжатия струи 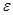= 1, а коэффициент = = 0,96…0,99.
Диффузорный насадок (рисунок 4.4, б) представляет собой комбинацию сопла и диффузора. Установка диффузора с оптимальным углом на выходе позволяет, не меняя проходного сечения отверстия (сечение 1-1) и расчетного напора, повысить расход жидкости почти в 2,5 раза по сравнению с расходом через сопло. Недостатком диффузорного насадка является склонность его к возникновению кавитации в узком сечении 1-1.
4.4 Истечение жидкости через проходные сечения в гидравлических устройствах
При определении расхода Q через проходные сечения, образованные взаимным расположением деталей в гидравлических устройствах, кроме оценки коэффициента расхода необходимо, как правило, определять площадь S проходного сечения отверстия в функции смещения х одной из деталей относительно другой. Обычно величина х и определяет степень открытия проходного сечения.
Для расчетов рекомендуется использовать формулу
,
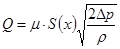где S(x) — расчетная площадь проходного сечения, определяемая по значению смещения х перекрывающей детали;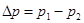
— перепад давления на проходном сечении.
Таблица 4.1 — Основные величины, характеризующие истечения
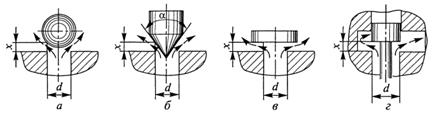
Тип детали, перекрывающей отверстие | Коэффициент расхода | Расчетная формула площади проходного сечения S(x) |
Шарик | 0,6…0,62 | πdx∙sin 45o |
Конус | 0,8…0,85 | πdx∙sin 45o |
Плоскость (x < d/4) | 0,8…0,85 | πdx |
Плунжер | 0,71…0,79 | πdx |
|
В таблице 4.1 и на рисунке 4.5 приведены основные варианты расчетных схем, полученные в результате анализа наиболее часто встречающихся случаев при решении задач определения расхода. В основном эти варианты отличаются формой детали, перекрывающей круглое проходное сечение диаметром d, и соотношением поперечных размеров отверстия и перекрывающей детали. Для каждого из них даются рекомендуемые значения коэффициента расхода в области квадратичного сопротивления и формула, позволяющая оценить площадь S(x) соответствующего проходного сечения.
14. Истечение жидкости через отверстия и насадки. Расчет скорости истечения и расхода жидкости при постоянном напоре.
Истечение жидкости через отверстие может происходить при постоянном и переменном напоре. Если истечение жидкости через отверстие происходит в атмосферу или другую газовую среду, то такое отверстие называется незаполненным. Если же истечение жидкости идет под уровень, а не в атмосферу -заполненным.
Сжатие называют неполным, если при подходе к отверстию поток с одной или нескольких сторон не испытывает сжатие.
Сжатие называют полным(совершенным), если расстояние от любой стороны контура до свободной поверхности жидкости или края стенки, в которой расположено отверстие, не будет меньше устроенного поперечного размера отверстия.
Отверстие
в тонкой стенке- это отверстие, диаметр
которого минимум в 3 раза больше толщины
стенки, т.е. d0>3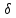
Насадком называется короткая труба длиной от 3 до 5 его диаметров, присоединенная к отверстию. При расчете насадков потерями напора по длине обычно пренебрегают.
Скорость истечения и вытекающий расход рассчитываются по общим формулам для отверстия и насадка, выведенным на основе уравнения Бернулли. Общими являются гидравлические характеристики: коэффициенты расхода, скорости, сжатия, сопротивления. Однако коэффициенты расхода для отверстия и насадка различны по величине, что связанно с различной картиной движения жидкости в них (рис.28 стр 55)
При истечении жидкости, через отверстие в тонкой стенке на некотором расстоянии от стенки, происходит сжатие струи. Площадь сечения струи будет меньше площади отверстия.(рис 27 а стр.55)
При истечении жидкости через насадок после входа в насадок жидкость сжимается примерно так же, как и при истечении через отверстие в тонкой стенке, а затем струя постепенно расширяется до размеров отверстия, и из насадка выходит полным сечением(рис.27 б, стр.55)
Сжатие струи характеризуется коэффициентом сжатия -отношение площади сечения струи в месте наибольшего сжатия к площади сечения отверстия.
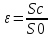
Где
Sc-площадь
живого сечения струи 
S0-площадь
отверстия
Коэффициент
сжатия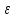 
для круглых отверстий равен 0,64, а для
цилиндрических насадков равен 1.
Для вывода уравнений расхода и скорости истечения через отверстие и насадок при постоянном уровне запишем уравнение Бернулли для идеальной жидкости для двух живых сечений 1-1 и 2-2, за плоскость сравнения примем сечение 2-2(рис.29. на стр.56)
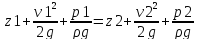
Тогда Z1=H, z2=0.
Скорость в сечении 1-1 v1=0, скорость в сечении 2-2 v2=vт (vт- теоретическая скорость истечения жидкости.)
Тогда 
Пусть у поверхности жидкости в резервуаре, давление равно атмосферному и истечение через отверстие происходит в пространство с атмосферным давлением, т.е p1=p2=pатм.
И теоретическая скорость истечения в этом случае рассчитывается:
Для реальной жидкости учитываются потери напора в сечении 2-2. Они обусловлены потерей напора hп на местном сопротивлении и определяется по формуле:
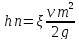
-коэффициент
местного сопротивления
Тогда формула для расчета действительной скорости истечения через отверстие будет выглядеть следующим образом:
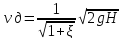
Величина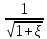 
называется коэффициентом скорости и
обозначается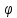
.
Коэффициент
скорости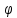 
представляет собой отношение действительной
скорости истечения к теоретической,
определяется опытным путем.
Зная скорость истечения жидкости можно определить расход жидкости через отверстие:
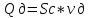
Где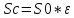 
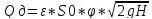
Где -коэффициент сжатия струи,
S0-площадь отверстия, м;
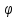-коэффициент
скорости
Произведение
коэффициента сжатия струи на коэффициент
скорости назыавается коэффициентом
расхода и обозначается 
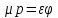
Коэффициентом
расхода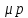 
называется отношение действительного
расхода к теоретическому:
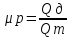
Тогда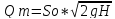 
Онлайн-калькулятор потерь напора в зависимости от расхода жидкости и сечения трубопровода
Эта версия статьи создана: 14.07.2020. Дата первой публикации: 28.08.2019
Зачем нужен этот калькулятор?
Калькулятор умеет рассчитывать потери напора в метрах в зависимости от длины и диаметра вашего трубопровода, а также объемного расхода жидкости. Зная потери напора, вы сможете более точно подобрать нужный насос под вашу задачу.
Наш калькулятор использует формулу расчета одного немецкого института гидродинамики. Из всех протестированных нами формул эта в наибольшей степени соотносится с нашим собственным опытом.
Чтобы воспользоваться калькулятором, введите исходные данные, потом нажмите кнопку «Рассчитать».
Ниже этой кнопки будут показаны результаты расчета.
Введите исходные данные
Внутренний диаметр трубопровода
мм
Длина трубопровода
м
Расход жидкости
л/мин
м³/ч
Перекачиваемая жидкость
==Другая жидкость==
Вода
Бензин
Нефть
Керосин
Масло И-20
Масло И-50
==Другая жидкость==
Кинематическая вязкость
м²/с
Введите значение вязкости вручную
Материал внутренней стенки трубопровода
==Указать шероховатость вручную==
Сталь
Чугун
Медь
Алюминий
Резина
Бетон
Полипропилен
==Указать шероховатость вручную==
Шероховатость внутренней поверхности трубы
мм
Введите данные вручную
Ускорение свободного падения в точке измерения
м/с²
Введите корректное ускорение, оно варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах.
Рассчитать
Результаты
Площадь сечения трубопровода: 0 мм²
Относительная шероховатость трубопровода: 0 мм
Скорость течения жидкости: 0 м/с
Число Рейнольдса: 0
Режим течения: 0
Коэффициент гидравлического трения: 0
Потери напора по длине: 0 м.в.ст
Подробнее о заполнении полей калькулятора
Поясним чуть подробнее как заполнить исходные данные.
-
Внутренний диаметр трубопровода
Измеряется в миллиметрах. Лучше измерять диаметр труб непосредственно штангенциркулем, а не ориентироваться на справочные данные. Также обратите внимание на то, что диаметр требуется именно внутренний. В каталогах труб часто указывают номинальный диаметр труб, который чуть больше, чем внутренний. -
Длина трубопровода
Измеряется в метрах. Длина трубопровода — это сумма длин всех прямых участков трубы, а не расстояние между начальной и конечной точкой. К примеру, если у вас труба идет 10 метров по земле, а затем поднимается на 3 метра вверх, и идет 2 метра в обратном направлении, то в калькулятор нужно занести число 15. Это важно учитывать на предприятиях, где трубы часто обходят препятствия и имеют технологические изгибы. -
Расход жидкости
В этом пункте вы самостоятельно можете выбрать единицы измерения: литры в минуту или кубометры в час. Расход жидкости — это количество жидкости, которое протекает через трубу за определенное время. Например, если 60 литровая бочка наполняется водой за 1 час, значит расход воды составляет 60 литров в час или 1 литр в минуту. -
Перекачиваемая жидкость
Для удобства в калькулятор уже занесены данные по кинематической вязкости некоторых жидкостей при температуре 20 °C. Если ваша жидкость присутствует в перечне, то просто выберите ее из выпадающего списка. Данные кинематической вязкости в поле ниже заполнятся автоматически. Если вашей жидкости в списке нет, то выберите пункт «Другая жидкость», после чего у вас появится возможность редактировать поле «Кинематическая вязкость» вручную. Кроме того, если температура перекачиваемой жидкости меньше 15 °С или больше 25 °С, то значение кинематической вязкости тоже лучше ввести вручную. -
Кинематическая вязкость
Измеряется в квадратных метрах в секунду. В большинстве случаев это поле заполняется автоматически. Однако если у вас есть данные по вязкости, лучше укажите это значение вручную. Для этого нужно выбрать в поле выше пункт «Другая жидкость», после чего откроется возможность ручного редактирования кинематической вязкости. Данные о кинематической вязкости можно взять из специализированных таблиц или измерить непосредственно при помощи вискозиметра. Обратите внимание, что вязкость сильно зависит от температуры жидкости — измеряйте ее при той же температуре, при которой она будет находиться в трубах. В данном калькуляторе используется система СИ, поэтому вводите данные именно в квадратных метрах в секунду. В таблицах данные часто указывают в сантистоксах: 1 сСт = 0.000001 м²/с. Не запутайтесь в количестве нулей! -
Материал внутренней поверхности трубопровода
Калькулятор содержит справочник материалов, из которых надо выбрать материал внутренней стенки трубопровода. Это нужно для определения шероховатости внутренней поверхности трубы. Если вы знаете шероховатость, то лучше указать ее вручную, выбрав пункт списка «Указать шероховатость вручную». После чего вам станет доступно для редактирования поле «Шероховатость внутренней поверхности». -
Шероховатость внутренней поверхности
Измеряется в условных миллиметрах. Эти данные можно взять из специализированных справочников.
Результаты расчёта
После того, как вы заполните данные, нажмите кнопку «Рассчитать». Калькулятор отобразит следующие показатели:
-
Площадь поперечного сечения трубопровода
Рассчитывается в квадратных миллиметрах. Этот показатель полезен для дальнейших расчетов. - Относительная ш
Истечение жидкости через отверстия и насадки — Студопедия
Истечение жидкости через отверстие может происходить при постоянном и переменном напоре. Если истечение жидкости через отверстие происходит в атмосферу или другую газовую среду, то такое отверстие называется незатопленным. Если же истечение идет под уровень, а не в атмосферу – затопленным.
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи. Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
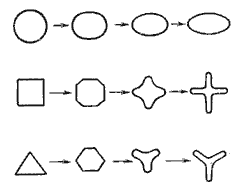
Рисунок – Инверсия струй
Рассмотрим истечение жидкости через отверстие в тонкой стенке при постоянном напоре. Отверстие в тонкой стенке – это отверстие, диаметр которого минимум в 3 раза больше толщины стенки, т.е. do> 3δ.
При истечении жидкости, через отверстие в тонкой стенке на некотором расстоянии от стенки (l = do), происходит сжатие струи. Площадь живого сечения струи будет меньше площади отверстия. Это объясняется тем, что частицы жидкости при входе в отверстие имеют скорости различных направлений.
Струя отрывается от стенки у кромки отверстия и затем несколько сжимается. Цилиндрическую форму струя принимает на расстоянии, равном примерно одному диаметру отверстия. Сжатие струи обусловлено необходимостью плавного перехода от различных направлений движения жидкости в резервуаре, в том числе от радиального движения по стенке, к осевому движению струи.
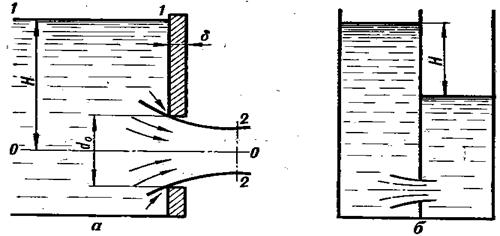
а – в атмосферу; б – под уровень жидкости
Рисунок — Истечение жидкости через отверстие в тонкой стенке
Сжатие струи характеризуется коэффициентом сжатия – отношение площади сечения струи в месте наибольшего сжатия к сечению отверстия.
,
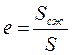где Scж — площадь живого сечения струи; S — площадь отверстия.
Коэффициент сжатия e определяется опытным путем и для круглых отверстий равен 0,64.
Задачей расчета истечения жидкостей является определение скорости и расхода при истечении. Скорость истечения определим по уравнению Бернулли. Для этой цели запишем уравнение Бернулли для реальной жидкости для двух живых сечений 1–1 и 2–2, проведя плоскость сравнения через ось отверстия:
В сечении 1-1 геометрический напор z1 = H, а в сечении 2-2 z2 = 0. Сосуд открыт, истечение через отверстие происходит в пространство с атмосферным давлением, следовательно p1 = p2 = pа. скоростью в поперечном сечении сосуда по сравнению со скоростью в отверстии можно пренебречь, т.е. принять w1 = 0. скорость в сечении 2-2 w2 = wс.
Сделав соответствующие подстановки и сокращения, получим:
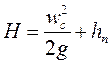
В выражении потери напора hп называются местным сопротивлением и определяются по формуле:
,
где ζ (зета) — коэффициент местного сопротивления (для входа в трубу без закругленных кромок ζ = 0,5, а с закругленными кромками ζ = 0,1).
Таким образом:
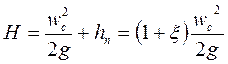
откуда окончательно получаем:
Величина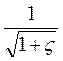 
называется коэффициент скорости и обозначается через φ. Коэффициент φ представляет собой отношение действительной скорости истечения к теоретической, определяется опытным путем.
Таким образом скорость истечения реальной жидкости:
,
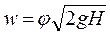Зная скорость истечения жидкости можно определить расход жидкости через отверстие:
,
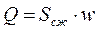Подставляя значения, для скорости и коэффициента сжатия получаем:
,
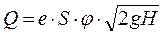где е – коэффициент сжатия струи,
S – площадь отверстия,
φ – коэффициент скорости,
Произведение коэффициента сжатия струи на коэффициент скорости называется коэффициентом расхода и обозначается μ. Следовательно:
,
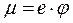И уравнение расхода через отверстие получает окончательный вид:
В практике часто приходится иметь дело с истечением жидкости не в атмосферу и не в газовую среду, а в пространство, заполненное этой жидкостью. Такой случай называется истечением под уровень или истечением через затопленное отверстие.
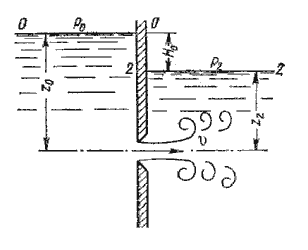 | В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении. |
| Рисунок — Истечение по уровень |
При истечении под уровень расчетные формулы для скорости и расхода остаются прежними, только H принимается как разность уровней.
При истечении через отверстие в боковой стенке напор не будет одинаковым для всех точек по сечению отверстия, в этом случае расход жидкости может быть определен путем суммирования, т.е. интегрирования элементарных расходов по всему сечению отверстия.
При истечении жидкости через короткий цилиндрический патрубок (насадок) происходит дополнительная потеря энергии, главным образом вследствии внезапного расширения струи в патрубке.
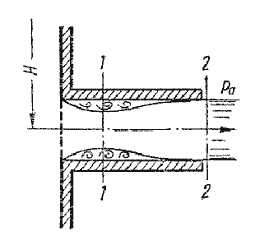
Рисунок — Истечение через насадок
Поэтому скорость истечения жидкости через патрубок меньше скорости ее истечения через отверстие в тонкой стенке. Вместе с тем, расход жидкости, вытекающей через патрубок больше, чем при истечении через отверстие. Так как струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке, а затем струя постепенно расширяется до размеров отверстия и из насадка выходит полным сечением. Поэтому коэффициент сжатия струи на выходе из патрубка е = 1, что приводит к повышению значения коэффициента расхода μ и соответственно расхода жидкости.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа.
Рисунок — Истечение жидкости через насадки а — расширяющиеся конические; б — сужающиеся конические; в — коноидальные; г — внутренние цилиндрические.
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
1.6 Расход жидкости через отверстия
1.6.1 Расход масла через отверстие или щель любой формы малой длины вычисляется по формуле:
,
л/мин,
где 
– коэффициент расхода; в диапазоне
Re=40-40000
=0,6-0,65
для отверстий с острыми кромками и
=0,8-0,9
для отверстий с притуплёнными или
закруглёнными кромками;
f
– площадь отверстия, мм2;
g = 9,81 м/с2; 
,
Н/м3; 
,
кг/м3;
–расчётная
разность давлений, под действием которой
происходит истечение, МПа.
Коэффициент расхода есть отношение действительного расхода к тому расходу, который имел бы место при отсутствии сжатия струи и сопротивления. Вследствие влияния этих двух факторов коэффициент расхода всегда меньше единицы.
Для масел, применяемых в станочных гидроприводах, расход через отверстие в тонкой стенке (диафрагме) можно принять равным:
,
л/мин (f,
мм2; 
р,
МПа).
1.6.2 Расход масла через капилляры – длинные каналы малого диаметра (l / d >20) – при ламинарном потоке
л/мин,
где d – диаметр канала, мм;
–перепад
давлений, МПа;
–коэффициент
динамической вязкости, Пас;
–коэффициент
кинематической вязкости, сСт; 
,
кг/м3;
l – длина канала, мм.
1.7 Гидравлический удар
Гидравлическим ударом обычно называют резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока жидкости. Точнее говоря, гидравлический удар представляет собой колебательный процесс, возникающий в упругом трубопроводе с жидкостью при внезапном изменении её скорости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления. Изменение давления при этом тесно связано с упругими деформациями жидкости и стенок трубопровода.
Гидравлический удар чаще всего возникает при быстром закрытии или открытии крана или иного устройства управления потоком. Однако могут быть и другие причины его возникновения.
Теоретическое и экспериментальное исследование гидравлического удара в трубах было впервые выполнено Н.Е.Жуковским и опубликовано в его фундаментальной работе «О гидравлическом ударе», вышедшей в свет в 1898 г.
1.8 Утечки
Наличие утечек масла в гидросистеме уменьшает его подачу и увеличивает потери мощности. Утечки оказывают значительное влияние на характеристики работы гидросистемы, снижают равномерность скорости рабочих движений и ограничивают диапазон регулирования скоростей.
Утечки
обычно происходят через зазоры,
представляющие узкие (капиллярные)
щели. Для них Reкр = 1000-1200. Число Рейнольдса зависит от
величины щели×
,
а поскольку размеры щели в гидроагрегатах
не превышают 10-15мкм, поток жидкости для
распространенных условий работы
(давлений и вязкости жидкостей) носит
обычно ламинарный характер.
1.8.1 Утечки через кольцевой зазор
Утечки масла через концентричный кольцевой зазор (рис. А4,а) между поршнем или плунжером и корпусом аппарата определяется по формуле:
где d – внутренний диаметр кольцевого зазора (диаметр поршня, золотника, плунжера), мм;
–радиальный
зазор, мкм;
=
p1 –
p2 — перепад давления в зазоре, МПа;
–абсолютная
вязкость масла, Па·с;
l – длина зазора вдоль оси, мм.
Если на поверхности поршня (плунжера) имеются кольцевые проточки (канавки), то в расчёт принимается длина поршня за вычетом длины кольцевых проточек (для примера по рис. А5 l = L – 2с).
Рис. А4 Рис. А5
Утечки в эксцентричной кольцевой щели (рис. А4,б) больше, чем в концентричной. При максимальном эксцентриситете е: Qут.э.к.з = 2,5 × Q ут.к.к.з.
% PDF-1.4 % 20 0 объект > endobj 23 0 объект (Содержание) endobj 24 0 объект > endobj 27 0 объект (Список рисунков) endobj 28 0 объект > endobj 31 0 объект (Номенклатура) endobj 32 0 объект > endobj 35 0 объект (Введение в Fluid Flow) endobj 36 0 объект > endobj 39 0 объект (Введение) endobj 40 0 объект > endobj 43 0 объект (Флюиды) endobj 44 0 объект > endobj 47 0 объект (Что такое жидкость?) endobj 48 0 объект > endobj 51 0 объект (Механика жидкости) endobj 52 0 объект > endobj 55 0 объект (Поток жидкости в приложениях химической инженерии) endobj 56 0 объект > endobj 59 0 объект (Свойства жидкостей) endobj 60 0 объект > endobj 63 0 объект (Гидростатика) endobj 64 0 объект > endobj 67 0 объект (Введение) endobj 68 0 объект > endobj 71 0 объект (Давление) endobj 72 0 объект > endobj 75 0 объект (Изменение давления в зависимости от положения в жидкости в состоянии покоя) endobj 76 0 объект > endobj 79 0 объект (Принцип Архимеда) endobj 80 0 объект > endobj 83 0 объект (Принцип Паскаля) endobj 84 0 объект > endobj 87 0 объект (Устройства измерения давления) endobj 88 0 объект > endobj 91 0 объект (Барометр) endobj 92 0 объект > endobj 95 0 объект (Манометры) endobj 96 0 объект > endobj 99 0 объект (Датчик Бурдона) endobj 100 0 объект > endobj 103 0 объект (Напор) endobj 104 0 объект > endobj 107 0 объект (Проблемы) endobj 108 0 объект > endobj 111 0 объект (Динамика потока \ 204 Идеальные жидкости) endobj 112 0 объект > endobj 115 0 объект (Введение) endobj 116 0 объект > endobj 119 0 объект (Режимы течения и число Рейнольдса) endobj 120 0 объект > endobj 123 0 объект (Баланс масс в трубе) endobj 124 0 объект > endobj 127 0 объект (Streamlines и Streamtubes) endobj 128 0 объект > endobj 131 0 объект (Уравнение непрерывности) endobj 132 0 объект > endobj 135 0 объект (Энергетический баланс) endobj 136 0 объект > endobj 139 0 объект (Потенциальная энергия) endobj 140 0 объект > endobj 143 0 объект (Кинетическая энергия) endobj 144 0 объект > endobj 147 0 объект (Энергия давления) endobj 148 0 объект > endobj 151 0 объект (Работай) endobj 152 0 объект > endobj 155 0 объект (Тепловые потери) endobj 156 0 объект > endobj 159 0 объект (Уравнение Бернулли) endobj 160 0 объект > endobj 163 0 объект (Приложения уравнения Бернулли) endobj 164 0 объект > endobj 167 0 объект (Поток из бака) endobj 168 0 объект > endobj 171 0 объект (Резервуары с постоянной высотой) endobj 172 0 объект > endobj 175 0 объект (Бак с переменной высотой) endobj 176 0 объект > endobj 179 0 объект (Измерение расхода) endobj 180 0 объект > endobj 183 0 объект (Измерение профиля скорости \ 205 Трубка Пито) endobj 184 0 объект > endobj 187 0 объект (Измеритель отверстия) endobj 188 0 объект > endobj 191 0 объект (Измеритель Вентури) endobj 192 0 объект > endobj 195 0 объект (Проблемы) endobj 196 0 объект > endobj 199 0 объект (Баланс моментума) endobj 200 0 объект > endobj 203 0 объект (Вывод уравнения импульса) endobj 204 0 объект > endobj 207 0 объект (Применение уравнения импульса) endobj 208 0 объект > endobj 211 0 объект (Поток через сужающийся участок трубопровода или через сопло) endobj 212 0 объект > endobj 215 0 объект (Обтекание сужающегося изгиба трубы) endobj 216 0 объект > endobj 219 0 объект (Резюме) endobj 220 0 объект > endobj 223 0 объект (Проблемы) endobj 224 0 объект > endobj 227 0 объект (Потери на трение — идеальные жидкости) endobj 228 0 объект > endobj 231 0 объект (Баланс сил на элементе жидкости) endobj 232 0 объект > endobj 235 0 объект (Прочие фитинги) endobj 236 0 объект > endobj 239 0 объект (Проблемы) endobj 240 0 объект > endobj 249 0 obj> поток x3T0
.Измерители расхода с отверстием, соплом и трубкой Вентури
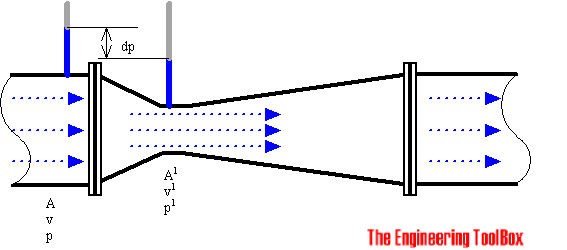
В расходомере, основанном на уравнении Бернулли, давление ниже по потоку после препятствия будет ниже, чем давление выше по потоку до него. Для понимания расходомеров с отверстиями, соплами и Вентури необходимо изучить уравнение Бернулли.
Уравнение Бернулли
Предполагая горизонтальный поток (пренебрегая незначительной разницей высот между точками измерения), уравнение Бернулли может быть изменено на:
p 1 + 1/2 ρ v 1 2 = p 2 + 1/2 ρ v 2 2 (1)
где
p = давление (Па, фунт / кв. дюйм)
ρ = плотность (кг / м 3 , снарядов / фут 3 )
v = скорость потока (м / с, дюйм / с)
Уравнение можно адаптировать для вертикального потока с помощью сложение высот :
p 1 + 1/2 ρ v 1 2 + γ h 1 = p 2 + 1/2 ρ v 2 2 + γ ч 2 9 0023 (1b)
, где
γ = удельный вес жидкости (кг / м 3 , пробок / дюйм 3 )
h = высота (м, дюйм)
Предполагая однородные профили скорости в верхнем и нижнем потоке — уравнение непрерывности может быть выражено как
q = v 1 A 1 = v 2 A 2 (2)
где
q = расход (м 3 / с, дюйм 3 / с)
A = проходное сечение (м 2 , в 2 )
Объединение (1) и (2) , при условии, что A 2 1 , дает «идеальное» уравнение:
900 08q = A 2 [2 (p 1 — p 2 ) / ρ (1 — (A 2 / A) 1 ) 2 )] 1/2 (3)
Для данной геометрии (A) расход может быть определен путем измерения разницы давлений p 1 — с 2 .
Теоретический расход q на практике будет меньше ( 2 — 40% ) из-за геометрических условий.
Идеальное уравнение (3) может быть изменено с помощью коэффициента расхода:
q = c d A 2 [2 (стр. 1 — p 2 ) / ρ (1 — (A 2 / A 1 ) 2 )] 1/2 (3b)
где
c d = Коэффициент расхода
Коэффициент расхода c d является функцией размера жиклера — или отверстия отверстия —
Соотношение площадей = A vc / A 2
где
A vc = площадь в «вене контракта» (м 2 , дюйм 90 015 2 )
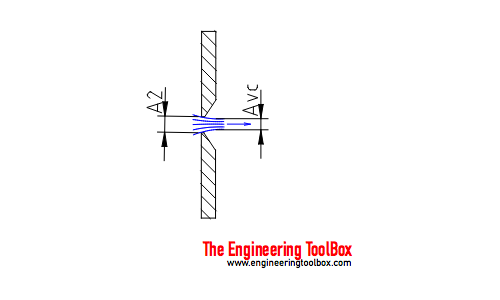
« Vena Contracta » — это минимальная площадь струи, которая появляется сразу после ограничения.Эффект вязкости обычно выражают через безразмерный параметр числа Рейнольдса — Re .
В соответствии с уравнением Бенулли и уравнением непрерывности скорость жидкости будет максимальной, а давление — минимальной в « Vena Contracta ». После дозатора скорость снизится до того же уровня, что и до препятствия. Давление восстанавливается до уровня ниже, чем давление перед препятствием, и добавляет потерю напора к потоку.
Уравнение (3) может быть изменено диаметрами на:
q = c d (π / 4) D 2 2 [2 (p 1 — p 2 ) / ρ (1 — d 4 )] 1/2 (4)
где
D 2 = внутренний диаметр сопла, Вентури или сопла (м, дюйм)
D 1 = диаметр трубы до и после трубы (м, дюйм)
d = D 2 / D 1 Отношение диаметров
π = 3.14 …
Уравнение (4) может быть преобразовано в массовый расход для жидкостей путем простого умножения на плотность:
m = c d (π / 4) D 2 2 ρ [2 (p 1 — p 2 ) / ρ (1 — d 4 )] 1/2 (5)
где
m = массовый расход (кг / s)
При измерении массового расхода в газах необходимо учитывать снижение давления и изменение плотности жидкости.Приведенная выше формула может использоваться с ограничениями для приложений с относительно небольшими изменениями давления и плотности.
Диафрагма
Диафрагма состоит из плоской диафрагмы с просверленным в ней круглым отверстием. Перед диафрагмой есть штуцер давления, а сразу после него — другой. Обычно существует три метода размещения кранов. Коэффициент метра зависит от положения кранов.
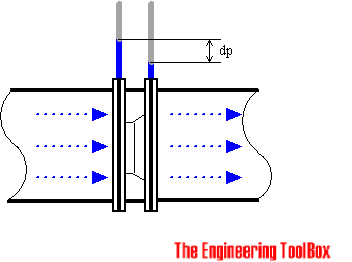
- Расположение фланца — Расположение штуцера давления 1 дюйм вверх по потоку и 1 дюйм вниз по потоку от торца отверстия
- Расположение « Vena Contracta » — Расположение штуцера давления 1 диаметр трубы (фактический внутри) перед и 0.От 3 до 0,8 диаметр трубы за лицевой стороной диафрагмы
- Расположение трубы — место отбора давления 2,5 раз больше номинального диаметра трубы до и в 8 раз больше номинального диаметра трубы за лицевой стороной диафрагмы
Коэффициент нагнетания — c d — значительно меняется в зависимости от соотношения площадей и числа Рейнольдса. Коэффициент расхода c d = 0,60 можно принять за стандартный, но его значение заметно меняется при малых значениях числа Рейнольдса.
| Коэффициент нагнетания — c d | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Отношение диаметров d = D 2 / D 1 | Число Рейнольдса — Re | 10 5 | 10 6 | 10 7 | |||||||
| 0,2 | 0,60 | 0,595 | 0.594 | 0,594 | |||||||
| 0,4 | 0,61 | 0,603 | 0,598 | 0,598 | |||||||
| 0,5 | 0,62 | 0,608 | 0,62 | 0,608 | 0,602 9050 9050 9050 | 0,608 | 0,608 | ||||
| 0,7 | 0,64 | 0,614 | 0,609 | 0,609 | |||||||
Восстановление давления ограничено для диафрагмы и степени постоянной потери давления в первую очередь.Для соотношения площадей 0,5 потеря напора составляет примерно 70–75% от перепада диафрагмы.
- Дроссельный расходомер рекомендуется для чистых и грязных жидкостей, а также для работы с некоторыми растворами.
- Диапазон изменения: 4–1
- Потеря давления средняя
- Типичная точность 2–4% полной шкалы
- Требуемый диаметр перед входом составляет 10–30
- Влияние вязкости высота
- Относительная стоимость низкая
Пример — расход через отверстие
Отверстие диаметром D 2 = 50 мм вставлено в стальную трубу 4 «Sch 40 с внутренним диаметром D 1 = 102 мм .Отношение диаметров может быть рассчитано как
d = (50 мм) / (102 мм)
= 0,49
Из приведенной выше таблицы коэффициент расхода можно оценить примерно как 0,6 для широкого диапазона число Рейнольдса.
Если жидкость представляет собой воду с плотностью 1000 кг / м 3 и перепад давления над отверстием составляет 20 кПа (20000 Па, Н / м 2 ) — массовый расход по трубе может быть рассчитывается из (5) как
m = 0.6 (π / 4) (0,05 м) 2 (1000 кг / м 3 ) [2 (20000 Па) / (1000 кг / м 3 ) (1 — 0,49 4 )] 1 / 2
= 7,7 кг / с
Калькулятор диафрагмы
Калькулятор диафрагмы основан на уравнении. 5 и может использоваться для расчета массового расхода через отверстие.
c d — коэффициент расхода
D 2 — диаметр отверстия (м)
D 1 — диаметр трубы (м)
p 1 — давление на входе ( Па)
p 2 — давление на выходе (Па)
ρ — плотность жидкости (кг / м 3 )
Типовая диафрагма K v Значения
| Размер диафрагмы (мм) | K v (м 3 / ч) | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.8 | 0,02 | |||||||||||||||||||||||||||||||||||||||||||||
| 1,2 | 0,05 | |||||||||||||||||||||||||||||||||||||||||||||
| 1,6 | 0,08 | |||||||||||||||||||||||||||||||||||||||||||||
| 2,4 | 0,17 | |||||||||||||||||||||||||||||||||||||||||||||
| 3,2 | 0,26 | 3,2 | 0,26 | 3,2 | 0,26 | 0,45 | ||||||||||||||||||||||||||||||||||||||||
| 6,4 | 0,60 | |||||||||||||||||||||||||||||||||||||||||||||
| 8 | 1,5 | |||||||||||||||||||||||||||||||||||||||||||||
| 9 | 1,7 | |||||||||||||||||||||||||||||||||||||||||||||
| 13 | 3 | ,5 | ||||||||||||||||||||||||||||||||||||||||||||
| 19 | 6,5 | |||||||||||||||||||||||||||||||||||||||||||||
| 25 | 11 | |||||||||||||||||||||||||||||||||||||||||||||
| 32 | 15 | |||||||||||||||||||||||||||||||||||||||||||||
| 38 | 22 | |||||||||||||||||||||||||||||||||||||||||||||
| 51 | ||||||||||||||||||||||||||||||||||||||||||||||
| 51 | ||||||||||||||||||||||||||||||||||||||||||||||
| 76 | 86 | |||||||||||||||||||||||||||||||||||||||||||||
| 80 | 99 | |||||||||||||||||||||||||||||||||||||||||||||
| 100 | 150 | |||||||||||||||||||||||||||||||||||||||||||||
| 125 | 264 | |||||||||||||||||||||||||||||||||||||||||||||
| 150 | ||||||||||||||||||||||||||||||||||||||||||||||
| 150 | 9045 инженеров-механиков (ASME).2001. Измерение расхода жидкости с помощью прецизионных расходомеров малого диаметра. ASME MFC-14M-2001.||||||||||||||||||||||||||||||||||||||||||||||
| Коэффициент нагнетания — c d | |||||||
|---|---|---|---|---|---|---|---|
| Соотношение диаметров d = D 2 / D 1 | Число Рейнольдса — Re | ||||||
| 10 5 | 10 6 | 10 7 | |||||
| 0.2 | 0,968 | 0,988 | 0,994 | 0,995 | |||
| 0,4 | 0,957 | 0,984 | 0,993 | 0,995 | |||
| 0,950 | 0,8 | 0,94 | 0,978 | 0,991 | 0,995 | ||
- Проточная форсунка рекомендуется как для чистых, так и для грязных жидкостей
- Диапазон изменения: от 4 до 1
- Относительная потеря давления составляет
- Типичная точность составляет 1-2% от полного диапазона
- Требуемая длина трубы перед входом составляет От 10 до 30 диаметров
- Влияние вязкости высокая
- Относительная стоимость средняя
Ссылки
- Американское общество инженеров-механиков neers ASME FED 01 января 1971 г.Расходомеры жидкости, их теория и применение — шестое издание
- Международная организация стандартов — ISO 5167-1: 2003 Измерение расхода жидкости с помощью устройств перепада давления, Часть 1: Диафрагмы, сопла и трубки Вентури, вставленные в круглое поперечное сечение трубопроводы заполнены. Ссылочный номер: ISO 5167-1: 2003.
Пример — расход керосина через расходомер Вентури
Перепад давления dp = p 1 — p 2 между входом и выходом составляет 100 кПа (1 10 5 Н / м 2 ) .Удельный вес керосина 0,82 .
Диаметр на входе 0,1 м и на выходе 0,06 м .
Плотность керосина может быть рассчитана как:
ρ = 0,82 (1000 кг / м 3 )
= 820 (кг / м 3 )
Площадь до и после можно рассчитать как:
A 1 = π ((0.1 м) / 2) 2
= 0,00785 (м 2 )
A 2 = π ((0,06 м) / 2) 2
= 0,002826 (м 2 )
Теоретический расход можно рассчитать по формуле (3):
q = A 2 [2 (p 1 — p 2 ) / ρ (1 — (A 2 / A 1 ) 2 )] 1/2
q = (0.002826 м 2 ) [2 (10 5 Н / м 2 ) / (820 кг / м 3 ) (1 — ((0,002826 м 2 ) / (0,00785 м 2 )) 2 )] 1/2
= 0,047 (м 3 / с)
Для перепада давлений 1 кПа (0,01×10 5 Н / м 2 ) — теоретический расход может быть рассчитан:
q = (0,002826 м 2 ) [2 (0,01 10 5 Н / м 2 ) / (820 кг / м 3 ) (1 — ((0.002826 м 2 ) / (0,00785 м 2 )) 2 )] 1/2
= 0,0047 (м 3 / с)
Массовый расход можно рассчитать как :
м = q ρ
= (0,0047 м 3 / с) (820 кг / м 3 )
= 3,85 (кг / с)
Расход Скорость и изменение перепада давления
Примечание! — Расход зависит от квадратного корня из разности давлений.
Из приведенного выше примера:
- для десятикратного увеличения расхода требуется стократное увеличение перепада давления!
Датчики и система управления
Нелинейная зависимость влияет на рабочий диапазон датчиков давления и требует, чтобы электронные датчики давления имели возможность линеаризовать сигнал перед его передачей в систему управления.
Точность
Из-за нелинейности скорость отклонения ограничена.Точность сильно возрастает в нижней части рабочего диапазона.
.Основы потока жидкости — AAPG Wiki
| Справочное руководство по геологии разработки | |
| серии | Методы разведки |
|---|---|
| Деталь | Методы разработки месторождений |
| Глава | Основы движения жидкости |
| Автор | Майкл Голан |
| Ссылка | Веб-страница |
| Магазин | Магазин AAPG |
Расчеты потока в скважине в основном сосредоточены на двух аспектах потока жидкости: профиле давления вдоль пути потока и зависимости дебита от давления в ключевых точках интереса (узлах), как показано на рисунке 1.Основные интересующие параметры (все в фунтах на квадратный дюйм):
- p R = пластовое давление
- p wf = давление потока в стволе (забое)
- p wh = устьевое давление
- p sp = давление в сепараторе
- p ST = давление в резервуаре
Соответствующие ставки
- q o = дебит нефти (баррелей резервуара STB / день)
- q г = дебит газа (стандартных кубических футов в сутки)
Перепад давления ( p R — p wf ) называется депрессией коллектора .Это основная сила, заставляющая пластовые флюиды поступать в ствол скважины. Как правило, производительность увеличивается с увеличением просадки. Как в ствол скважины, вызванной депрессией, называется приток .
Взаимосвязь между дебитом дебита, измеренным в резервуаре для хранения, q o , и забойным давлением потока, p wf , называется отношением производительности притока (1PR) . IPR скважины может быть определен непосредственно по данным производственного испытания или может быть спрогнозирован по данным коллектора.Независимо от того, представлен ли он графически или выражен формулой, IPR является заявлением о производственной мощности и широко используется для проектирования и анализа производительности скважин.
Хорошие общие ссылки на поток в коллекторах и скважинах включают Golan and Whitson, [1] Bradley, [2] и Craft et al. [3]
Эмпирические уравнения ПИС
Рисунок 1 Условия давления в простой производственной системе. ,Численное исследование потока жидкости в трубе, изогнутой под углом 90 градусов с большой степенью кривизны РецензентамДля редакцииОглавлениеСпециальные выпускиПодатьМатематические проблемы в технике / 2015 / СтатьяСтатья Разделы
На этой странице
АннотацияВведениеМодель ,