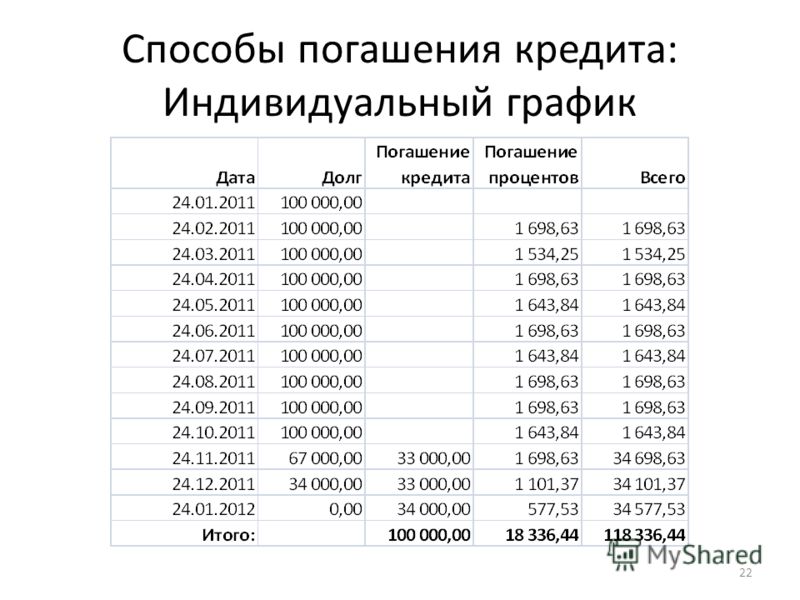
Заемщики смогут сами выбрать способ погашения долга

Согласно инициативе, банк должен будет предоставить гражданину возможность выбрать вид ежемесячного платежа для погашения займа, не связанного с предпринимательской деятельностью. Как отмечается в пояснительной записке, в настоящее время большинство банков не представляет потребителю права выбора, что вызывает раздражение и социальную напряженность в среде заемщиков. Заемщикам на рассмотрение будут предоставлены два вида платежа: аннуитетный либо дифференцированный. 

Считается, что погашение задолженности аннуитетным платежом удобнее, т. к. все платежи равны. Но при этом переплата значительно больше. В свою очередь дифференцированный платеж дает возможность заемщику потратить существенно меньше средств на оплату процентов. Однако первый платеж при этом больше, чем при аннуитетном. Кроме того, в зависимости от дохода заемщика отличается сумма доступного кредита: при дифференцированном платеже доход должен быть ощутимо выше (20–25%).

Достаточно распространены случаи, когда заемщик оплачивает первоначальный взнос, в течение нескольких лет производит погашение, а по суду, с учетом начисленных процентов и пени, его долг больше полученной от кредитора суммы. По мнению заемщиков, основной причиной возникновения подобной ситуации является отсутствие права выбора вида ежемесячного платежа.

Ожидается, что в результате реализации законопроекта граждане смогут самостоятельно оценить положительные и отрицательные стороны двух способов погашения долга и нести ответственность за собственный выбор.

Законодательная инициатива внесена в Государственную Думу Андреем Барышевым Барышев
Андрей Викторович Депутат Государственной Думы избран по избирательному округу 0189 (Челябинский – Челябинская область) .

Аннуитетный платеж — это равный по сумме вид ежемесячного платежа, который включает в себя сумму начисленных процентов за кредит и сумму основного долга.

Дифференцированный платеж — это вид ежемесячного платежа, который включает в себя сумму основного долга, выплачиваемого равными долями и проценты, начисляются на остаток основного долга.

Банк | Часто задаваемые вопросы

Есть ли лимит на снятие наличных денежных средств?

Да, есть. Лимит устанавливается в месяц в зависимости от валюты счета Карты. Лимиты указаны в Тарифах Банка по обслуживанию банковских расчетных карт для физических лиц.

Что такое дебетовая (расчетная) карта?

Банковская карта одной из международных платежных систем, например, «Visa», «Mastercard Worldwide», предназначенная для совершения операций ее держателем в пределах установленного платежного лимита карты, расчеты по которой осуществляются за счет денежных средств клиента, размещенных на его Карточном счете.

Можно ли самостоятельно изменить ПИН-код по Карте?

Да, можно в банкоматах Банка. Комиссия будет взиматься в соответствии с Тарифами Банка.

Можно ли изменить номер мобильного телефона для предоставления услуги SMS-информирования?

Да, можно в банкоматах Банка. Данная услуга оказывается бесплатно.

Начисляются ли проценты на остаток на Карточном счете?

Нет, не начисляются.

Куда звонить при утере, краже Карты?

Держателю Карты необходимо немедленно сообщить в Банк для блокировки Карты по телефонам: в службу круглосуточной поддержки по телефону +7 (495) 785-15-15 или +7 (495) 228-12-44 в часты работы Банка

Что делать, если Клиент не согласен с транзакцией?

При несогласии с транзакцией по Карте клиенту необходимо обратиться по данному вопросу в Банк или его отделение для формирования выписки и подачи заявления о несогласии с транзакцией.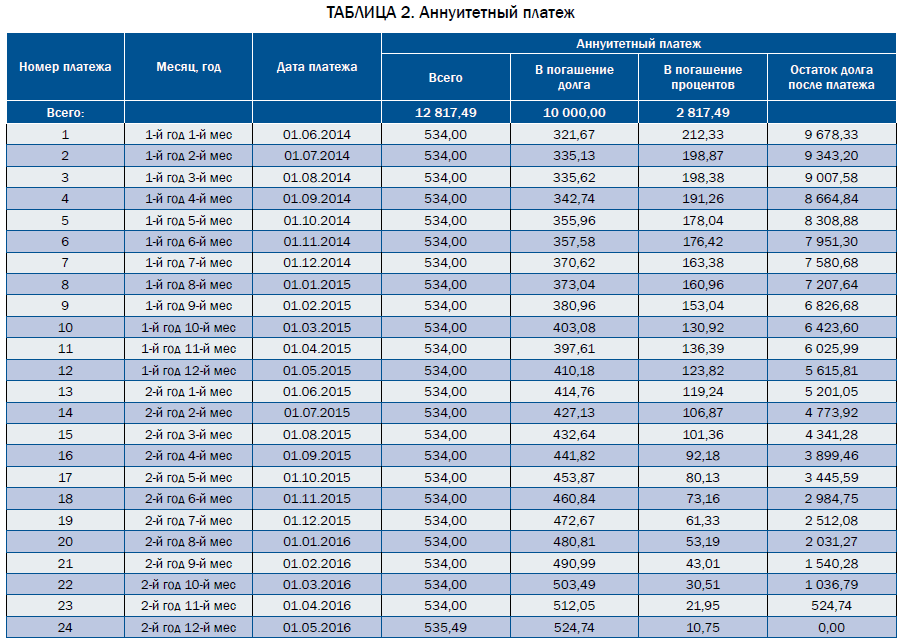

Какие операции относятся к валютным?

Для целей  Федерального закона   от 10.12.2003 г. № 173-ФЗ «О валютном регулировании и валютном контроле».     используются следующие основные понятия:
Валютными операциями для резидента являются:

а) приобретение резидентом у резидента и отчуждение резидентом в пользу резидента валютных ценностей на законных основаниях, а также использование валютных ценностей в качестве средства платежа;

Резиденты и нерезиденты- кто попадает под данное понятие?

Определение  резидентов и  нерезидентов определяется Федеральным Законом от 10. 12.2003 г. № 173-ФЗ «О валютном регулировании и валютном контроле».

      Резиденты:
а) физические лица, являющиеся гражданами Российской Федерации;
б) постоянно проживающие в Российской Федерации на основании вида на жительство, предусмотренного законодательством Российской Федерации, иностранные граждане и лица без гражданства;

Валютные операции между резидентами запрещены. Есть ли исключения из данного правила?

Расчеты в иностранной валюте между резидентами запрещены, за исключением операций, указанных в статье 9 Федерального Закона от 10.12.2003 г. № 173-ФЗ «О валютном регулировании и валютном контроле».

Какие виды кредитов выдает КБ «Крокус-Банк» (ООО)?

Кредиты физическим лицам:
— на потребительские нужды;
— ипотечные кредиты – на приобретение жилья, другой недвижимости;
— на потребительские нужды под залог недвижимости;
— автокредиты.
Кредитные продукты для юридических лиц:
— на пополнение оборотных средств;
— инвестиционные кредиты – на приобретение основных средств, недвижимости;
— кредиты в форме овердрафта;
— кредиты под инкассируемую выручку;
— тендерные кредиты – на обеспечение конкурсной заявки, на исполнение контрактов;
— банковские гарантии.

Что такое полная стоимость кредита (ПСК) и почему она больше процентной ставки по кредиту?

При предоставлении кредита физическому лицу или изменении условий по нему банк обязан проинформировать клиента о полной стоимости кредита (ПСК). Полная стоимость кредита учитывает все возможные платежи заемщика, платежи в пользу третьих лиц (например, услуги по страхованию), определенные договором. ПСК вычисляется в процентах годовых и рассчитывается с учетом суммы, срока и процентной ставки за пользование кредитом.

Что такое аннуитетный способ погашения (аннуитетный платеж)?

Аннуитетный способ погашения кредита — это такой способ, при котором вы погашаете кредит, ежемесячно равными платежами. Исключение составляет последний платеж, который может отличаться от ежемесячного платежа, поскольку является остаточным. Аннуитетный платеж включает в себя сумму основного долга и начисленные проценты по кредиту. В настоящее время подавляющее большинство банков использует именно такую схему расчета ежемесячного платежа. Такая схема удобна, потому что вы всегда знаете, сколько нужно заплатить по кредиту.

Где и как я могу получить кредит наличными?

Оформить заявку на получение кредита наличными вы можете легко и удобно прямо на сайте Крокус-Банка, а также, обратившись в любое дополнительный офис Банка.

Где и как я могу погашать кредит наличными?

Кредит необходимо погашать ежемесячно равными платежами не позднее даты, указанной в вашем графике погашения. Крокус-Банк предлагает много способов погашения кредита: узнать подробнее и выбрать подходящий именно вам способ вы можете на сайте. Также способы погашения кредита описаны в вашем кредитном договоре.

Каким образом я могу выразить свое согласие заключить Договор страхования жизни на случай потери трудоспособности?

Если вы желаете обезопасить себя от непредвиденных жизненных обстоятельств и хотите присоединиться к Коллективному договору страхования от несчастных случаев и болезней, то просто сообщите об этом при заполнении заявки в отделении Банка.

Могу ли я досрочно погасить задолженность по кредиту?

Кредит можно погасить досрочно: частично или полностью без каких либо штрафов и комиссий при условии заполнения заявления на досрочное гашение.

Что будет, если я забыл погасить кредит в срок?

Если вы забыли внести ежемесячный платеж, сделайте это как можно скорее любым из возможных способов погашения кредита. Потому что за неуплату ежемесячного платежа в срок, указанный в графике погашения, взимается неустойка согласно индивидуальным условиям кредитования.

Я получаю зарплату на карту Крокус-Банка. Есть ли для меня специальное предложение?

Да. Вы можете рассчитывать на персональное предложение по кредиту наличными с пониженной процентной ставкой.

Если я проживаю и работаю в Москве/Московской области, а регистрация у меня в другом городе, могу ли я оформить кредит в КБ «Крокус-Банк» (ООО)?

В вашем случае КБ «Крокус-Банк» (ООО) может рассмотреть вашу кредитную заявку при условии предоставления поручительства физического лица с регистрацией в Москве или Московской области.

Способы погашения кредита | Платежи по кредитам

Способы погашения кредита

Когда вы берете кредит у банков вам обязательно нужно вносить ежемесячные выплаты.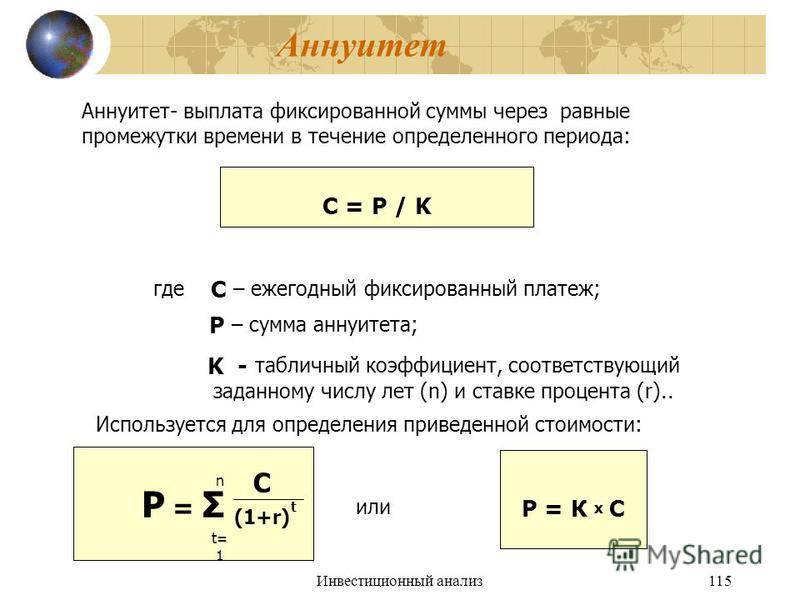 Ежемесячные выплаты по кредиту могут быть осуществлены двумя способами: равными или разделенными по сумме платежами. Называются они аннуитетный или дифференцированный способы погашения кредита. Разберем подробно каждый из них.

Аннуитетный способ погашения кредита – это такой способ выплаты по кредиту, когда нужно перечислять в банк одинаковую сумму согласно графику выплат по кредиту. Когда вы берете кредит, предусматривающий большой срок, то большую часть платежей в первые месяцы составят проценты. Основной долг по кредиту будет уменьшаться постепенно.

Рассмотрим пример с помощью кредитного калькулятора Finlit.uz:

Предположим, вы хотите взять кредит в размере 10 000 000 сумов на 6 месяцев по ставке 23% годовых.

Сумма ежемесячных выплат составит 1 780 240,71 сумов

В каждом месяце соотношение суммы погашения кредита и суммы процентов будет изменяться. В первом месяце вы выплатите 1& 588& 574,05 сумов основного долга и 191 666,67 сумов процентов. В последнем месяце сумма основного долга будет 1 746 761,13 сумов, а процентная часть из выплаты составит всего лишь 33 479,59 сумов.

Общая сумма кредита, которую вы выплатите банку составит 10681444,29 сумов.

Если срок кредита более длительный, то при погашении соотношение суммы основного долга и суммы процентов изменится.

Рассмотрим тот же пример, но с измененными условиями:

Предположим, вы хотите взять кредит в размере 10 000 000 сумов,
но уже не на 6 месяцев, а на 2 года (24 месяца) по ставке 23% годовых. При данных условиях:

Сумма ежемесячных выплат составит 523 733,06 сумов.

В первом месяце вы выплатите 332 066,39 сумов основного долга и 191 666,67 сумов процентов – первый платеж состоит примерно наполовину из процентной части, а в последнем месяце процентная часть из выплаты составит всего лишь 9 849,44 сумов.

Общая сумма кредита, которую вы выплатите банку составит 12 569 593,45 сумов.

Дифференцированный способ погашения кредита – это способ погашения кредита, при котором каждый месяц выплачивается равная сумма основного долга, а проценты постепенно убывают одновременно с уменьшением остатка кредита.

Первые месяцы выплат являются самыми большими и снижаются с каждым месяцем. В последний месяц сумма выплат значительно меньше суммы первого месяца.

Рассмотрим пример с такими же условиями и с помощью кредитного калькулятора Finlit.uz

Кредит в размере 10 000 000 сумов на 6 месяцев по ставке 23% годовых. При дифференцированном способе погашения кредита размер ежемесячных выплат будет такой:

Сумма ежемесячных выплат различается.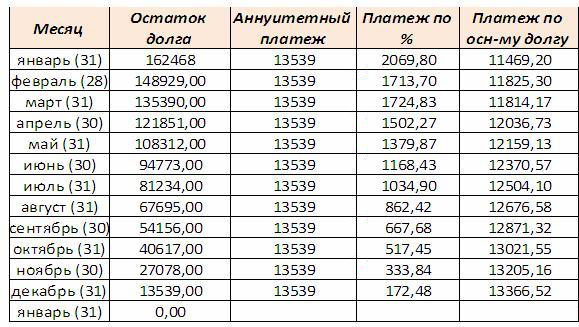 Так платеж первого месяца составит 1 55 707,76 сумов – из них 189 041,10 процентов. Платеж последнего (6) месяца составит 1 698 173,52 сумов – из них 31 506,85 процентов.

Общая сумма кредита, которую вы выплатите банку составит 10 672 146,12 сумов.

В случае увеличения срока, предположим до 24 месяцев, первый платеж будет в размере 605 707,76 сумов из которых 189 041,10 сумов составят проценты. Платеж последнего (24) месяца составит 424 805,94 сумов – из них 8 139,27 процентная часть.

При условии, что срок кредита составляет 2 года, общая сумма выплат по кредиту составит 12 398 721,46 сумов.

Сопоставив примеры выплат по кредиту на 10 000 000 сумов, можно заметить, что дифференцированный способ погашения выгоднее аннуитетного на 9 298,17 сумов и на 170 871,99 сумов для кредитов сроком 6 месяцев и 2 года соответственно.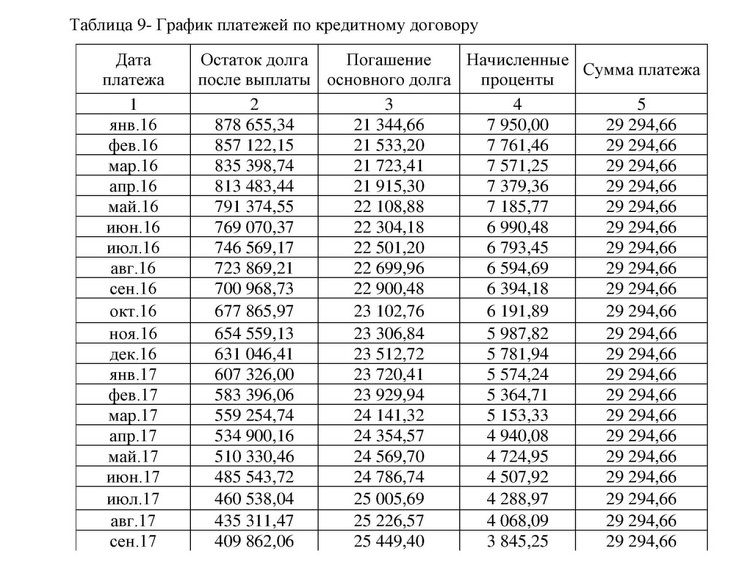

Если сравнить погашение кредита аннуитетными и дифференцированными способами, то при одинаковых условиях кредита выплата в первом случае оказывается несколько больше.

Преимущества и недостатки данных способов погашения:

Аннуитетный способ погашения кредита:

+ вы точно знаете какую сумму нужно платить каждый месяц. Зная свои расходы по кредитным обязательствам, вы более тщательно сможете планировать свой бюджет.

— первые платежи включают большую долю процентов и только малую часть основного долга.

Дифференцированный способ погашения кредита:

+ расходы по кредиту будут уменьшаться к концу срока, так как основная сумма, и проценты будут намного меньше, чем при первых платежах.

— большая финансовая нагрузка при первых выплатах по кредиту.

Помните! Проценты начисляются на остаток основной суммы кредита. Погашая платежи по кредиту большей суммой, чем указано в графике погашения, вы уменьшаете сумму начисленных процентов в следующем месяце

Аннуитет, подлежащий выплате

Сколько причитается аннуитет?

Аннуитет — это аннуитет, выплата которого производится немедленно в начале каждого периода. Распространенным примером причитающейся выплаты аннуитета является арендная плата, поскольку домовладельцы часто требуют уплаты в начале нового месяца, а не взыскания после того, как арендатор пользовался льготами от квартиры в течение всего месяца.

Ключевые выводы

• Аннуитетный платеж — это аннуитет, выплата которого производится немедленно в начале каждого периода.
• Причитающийся аннуитет можно сравнить с обычным аннуитетом, когда выплаты производятся в конце каждого периода.
• Типичный пример причитающейся аннуитета — арендная плата, выплачиваемая в начале каждого месяца.
• Пример обычного аннуитета включает ссуды, такие как ипотека.
• Формулы текущей и будущей стоимости подлежащего выплате аннуитета немного отличаются от формул для обычного аннуитета, поскольку они учитывают разницу в сроках осуществления платежей.

Как работает аннуитет

Для выплаты аннуитета требуются выплаты в начале, а не в конце каждого периода аннуитета.Причитающиеся аннуитетные платежи, полученные физическим лицом, по закону представляют собой актив. Между тем, лицо, выплачивающее аннуитет, имеет юридическое долговое обязательство, требующее периодических выплат.

Поскольку серия причитающихся платежей по аннуитету отражает ряд будущих притоков или оттоков денежных средств, плательщик или получатель средств может пожелать рассчитать полную стоимость аннуитета с учетом временной стоимости денег. Этого можно добиться, используя расчеты приведенной стоимости.

В таблице приведенной стоимости подлежащего выплате аннуитета прогнозируемая процентная ставка указана в верхней части таблицы, а количество периодов — в крайнем левом столбце. Пересекающаяся ячейка между соответствующей процентной ставкой и количеством периодов представляет множитель приведенной стоимости. Нахождение продукта между одним причитающимся платежом по аннуитету и множителем приведенной стоимости дает текущую стоимость денежного потока.

Причитающийся пожизненный аннуитет — это финансовый продукт, продаваемый страховыми компаниями, который требует выплаты аннуитета в начале каждого ежемесячного, ежеквартального или годового периода, а не в конце периода. Это тип аннуитета, который будет обеспечивать держателя выплат в течение периода распределения на протяжении всей его жизни.После того, как аннуитет переходит, страховая компания удерживает оставшиеся средства.

Доходные выплаты по аннуитету облагаются налогом как обычный доход.

Аннуитетная задолженность по сравнению с обычной аннуитетом

Причитающаяся аннуитетная выплата — это повторяющаяся выдача денег в начале периода. В качестве альтернативы, обычная аннуитетная выплата представляет собой повторяющуюся выдачу денег в конце периода. Контракты и деловые соглашения определяют этот платеж, и он зависит от того, когда была получена выгода.При оплате расходов получатель уплачивает причитающуюся аннуитетную выплату до получения выплаты, в то время как получатель производит обычные причитающиеся платежи после выплаты пособия.

Время выплаты аннуитета имеет решающее значение с учетом альтернативных издержек. Сборщик платежа может инвестировать аннуитетный платеж, полученный в начале месяца, для получения процентов или прироста капитала. Вот почему аннуитет более выгоден для получателя, поскольку у него есть возможность быстрее использовать средства.В качестве альтернативы, люди, выплачивающие аннуитет, теряют возможность использовать средства в течение всего периода. Таким образом, выплачивающие аннуитеты, как правило, предпочитают обычные аннуитеты.

Примеры аннуитета

Аннуитет может возникнуть в связи с любыми повторяющимися обязательствами. Многие ежемесячные счета, такие как аренда, ипотека, оплата автомобиля и сотового телефона, являются аннуитетами, поскольку получатель должен оплатить в начале расчетного периода.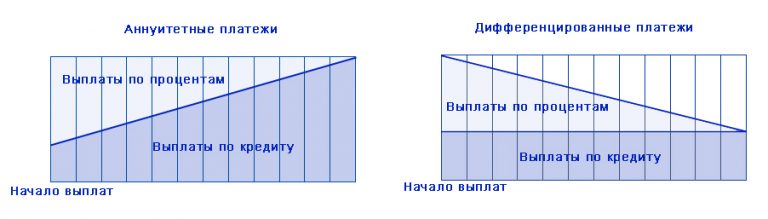 Расходы на страхование обычно представляют собой аннуитетные выплаты, поскольку страховщик требует выплаты в начале каждого периода страхового покрытия.Ситуации, связанные с выплатой аннуитета, также обычно возникают в связи с накоплением на пенсию или отложением денег на определенную цель.

Как рассчитать размер аннуитета

Настоящая и будущая стоимость причитающейся аннуитета может быть рассчитана с использованием небольших изменений текущей стоимости и будущей стоимости обычной аннуитета.

Приведенная стоимость аннуитета

Приведенная стоимость причитающейся аннуитета показывает нам текущую стоимость ряда ожидаемых аннуитетных платежей.Другими словами, он показывает, сколько сейчас стоит будущая сумма, подлежащая выплате.

Расчет приведенной стоимости причитающейся аннуитета аналогичен расчету приведенной стоимости обычной аннуитета. Однако есть тонкие различия, которые необходимо учитывать при наступлении срока выплаты аннуитета.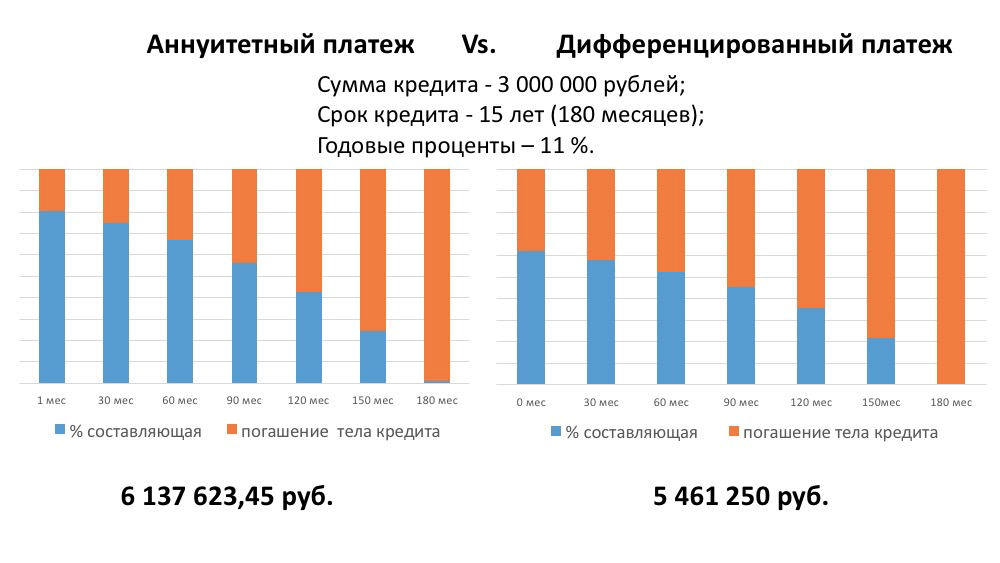 Для причитающегося аннуитета выплаты производятся в начале интервала, а для обычного аннуитета выплаты производятся в конце периода. Формула для определения текущей стоимости причитающегося аннуитета:

С участием:

• C = Денежные потоки за период
• i = процентная ставка
• n = количество платежей

Давайте посмотрим на пример приведенной стоимости подлежащего выплате аннуитета. Предположим, вы являетесь бенефициаром, которому назначено немедленное получение 1000 долларов США в год в течение 10 лет с годовой процентной ставкой 3%. Вы хотите знать, сколько стоит для вас поток платежей сегодня. Исходя из формулы приведенной стоимости, приведенная стоимость составляет 8 786 долларов.11.

Будущая стоимость аннуитета

Будущая стоимость подлежащего выплате аннуитета показывает нам конечную стоимость ряда ожидаемых платежей или стоимость в будущем.

Подобно тому, как существуют различия в том, как рассчитывается приведенная стоимость для обычного аннуитета и аннуитета к выплате, существуют также различия в том, как рассчитывается будущая стоимость денег для обычного аннуитета и подлежащего выплате аннуитета. Будущая стоимость аннуитета рассчитывается как:

Используя тот же пример, мы вычисляем, что будущая стоимость потока выплат дохода будет 11 807,80 долларов США.

Часто задаваемые вопросы о выплате аннуитета

Что лучше: обычная рента или рента с уплатой?

Что лучше — обычная аннуитет или аннуитет, зависит от того, являетесь ли вы получателем или плательщиком. Как получатель платежа, аннуитет часто предпочтительнее, потому что вы получаете аванс на определенный срок, что позволяет вам использовать средства немедленно и получать более высокую приведенную стоимость, чем у обычного аннуитета. Для плательщика обычная рента может быть выгодной, поскольку вы вносите платеж в конце срока, а не в начале. Вы можете использовать эти средства в течение всего периода до оплаты.

Часто вам не предоставляется возможность выбора. Например, страховые взносы являются примером подлежащего уплате аннуитета, при этом страховые взносы подлежат уплате в начале страхового периода. Плата за автомобиль является примером обычного аннуитета, при котором платежи подлежат оплате в конце периода покрытия.

Что такое немедленная рента?

Немедленный аннуитет — это счет, финансируемый за счет единовременного депозита, который генерирует немедленный поток выплат дохода.Доход может составлять заявленную сумму (например, 1000 долларов в месяц), заявленный период (например, 10 лет) или всю жизнь.

Как рассчитать будущую стоимость аннуитета?

Будущая стоимость аннуитета рассчитывается по формуле:

где

• C = Денежные потоки за период
• i = процентная ставка
• n = количество платежей

Что означает аннуитет?

Аннуитет — это страховой продукт, предназначенный для получения платежей сразу или в будущем владельцу аннуитета или назначенному получателю. Владелец счета производит либо единовременную выплату, либо серию платежей в аннуитет и может либо получать немедленный поток дохода, либо отложить получение платежей до некоторого времени в будущем, обычно после периода накопления, когда на счете начисляются отсроченные по налогу на прибыль проценты. .

Что происходит по истечении срока годности?

По истечении срока годности договор прекращается, и будущие платежи не производятся. Обязательства по контракту выполнены, и ни одна из сторон не возьмет на себя никаких дальнейших обязательств.

Итог

Аннуитет — это аннуитет, причитающийся или производимый в начале платежного интервала. Напротив, при обычном аннуитете выплаты производятся в конце периода. В результате методы расчета настоящей и будущей стоимости различаются. Типичный пример причитающейся аннуитета — это арендная плата, выплачиваемая домовладельцу, а типичный пример обычного аннуитета включает выплаты по ипотеке, выплачиваемые кредитору. В зависимости от того, плательщик вы или получатель, аннуитет может быть лучшим вариантом.

6.4: Приведенная стоимость аннуитета и выплаты в рассрочку

НАСТОЯЩАЯ СТОИМОСТЬ ГОДА

В Разделе 6.2 мы научились определять будущую стоимость единовременной выплаты, а в Разделе 6.3 мы научились определять будущую стоимость аннуитета. Имея в руках эти две концепции, мы теперь научимся амортизировать ссуду и определять приведенную стоимость аннуитета.

Приведенная стоимость аннуитета — это сумма денег, которая нам понадобится сейчас, чтобы иметь возможность производить платежи аннуитета в будущем.Другими словами, текущая стоимость — это текущая стоимость будущего потока платежей.

Мы начнем с разбивки этого шага за шагом, чтобы понять концепцию приведенной стоимости аннуитета. После этого примеры предоставляют более эффективный способ выполнения расчетов, работая с концепциями и расчетами, которые мы уже исследовали в разделах 6.2 и 6.3.

Предположим, Карлос владеет малым бизнесом и нанимает помощника менеджера, который помогает ему управлять бизнесом. Предположим, сейчас 1 января.Карлос планирует выплатить своему помощнику менеджера премию в размере 1000 долларов в конце этого года и еще одну премию в размере 1000 долларов в конце следующего года. В этом году у Карлоса была хорошая прибыль, поэтому он хочет сейчас положить деньги на будущие бонусы своего помощника на сберегательный счет. Деньги, которые он вкладывает сейчас, будут приносить проценты по ставке 4% в год, начисляемые ежегодно на сберегательном счете.

Сколько денег Карлосу следует положить на сберегательный счет сейчас, чтобы он мог снять 1000 долларов через год и еще 1000 долларов через два года?

Сначала это звучит как фонд погашения.Но это другое. В фонде погашения мы вкладываем деньги в фонд с периодическими выплатами для накопления до определенной единовременной суммы, которая является будущей стоимостью в конце определенного периода времени. {1} \ text {so} P_ {1} = \ $ 961.{2} \ text {so} P_ {2} = \ $ 924.56 \ nonumber \]

Чтобы произвести платежи в размере 1000 долларов США в указанное время в будущем, сумма, которую Карлос должен внести сейчас, представляет собой текущую стоимость \ (P = P_ {1} + P_ {2} = \ 961,54 доллара США + \ 924,56 доллара США = \ $ 1886.10 \)

Приведенный выше расчет был полезен, чтобы проиллюстрировать значение приведенной стоимости аннуитета.
Но это не эффективный способ расчета приведенной стоимости. Если бы у нас было большое количество аннуитетных платежей, пошаговый расчет был бы долгим и утомительным.

Example \ (\ PageIndex {1} \) исследует и разрабатывает эффективный способ расчета текущей стоимости аннуитета, связывая будущую (накопленную) стоимость аннуитета и его текущую стоимость.

Пример \ (\ PageIndex {1} \)

Предположим, вы выиграли лотерею, по которой выплачивается 1000 долларов в месяц в течение следующих 20 лет. Но вы предпочитаете получить всю сумму сейчас.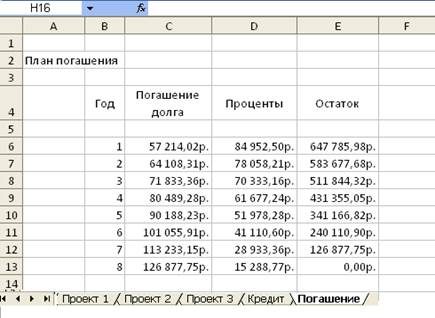 Если процентная ставка 8%, сколько вы примете?

Решение

Рассмотрим для целей аргумента, что два человека, мистер Кэш и мистер Кредит, выиграли одну и ту же лотерею на 1000 долларов в месяц в течение следующих 20 лет. Г-н Кредит доволен своим ежемесячным платежом в 1000 долларов, но г-н Кэш хочет получить всю сумму сейчас.

Наша задача — определить, сколько должен получить мистер Кэш. Мы рассуждаем так:

Если мистер Кэш принимает P-доллары, то P-доллары, депонированные под 8% на 20 лет, должны принести ту же сумму, что и ежемесячные платежи в размере 1000 долларов в течение 20 лет.{240} -1 \ right]} {. 08/12} \\
\ mathrm {P} (4.9268) = \ $ 1000 (589.02041) \\
\ mathrm {P} (4.9268) = \ $ 589020.41 \\
\ mathrm {P} = \ 119 554,36 долл. США
\ end {array} \ nonumber \]

Приведенная стоимость обычной ренты в размере 1000 долларов США в месяц в течение 20 лет под 8% составляет 119 554,36 долларов США

Читателю следует также отметить, что если мистер Кэш возьмет свою единовременную выплату в размере \ (\ mathrm {P} \) = 119 554,36 долларов США и вложит ее в размере 8% ежемесячно, его совокупная стоимость составит \ (\ mathrm {A} \) = 589 020 долларов.41 за 20 лет.

РАССРОЧКА ПО КРЕДИТУ

Если физическому или юридическому лицу необходимо купить или заплатить за что-то сейчас (автомобиль, дом, обучение в колледже, оборудование для бизнеса), но у него нет денег, они могут занять деньги в качестве ссуды.

Они получают сумму ссуды, называемую основной суммой (или приведенной стоимостью) сейчас, и обязаны выплатить основную сумму в будущем в течение установленного периода времени (срока ссуды) в виде регулярных периодических платежей с процентами.

Пример \ (\ PageIndex {2} \) исследует, как рассчитать платеж по ссуде, используя рассуждения, аналогичные Примеру \ (\ PageIndex {1} \).

Пример \ (\ PageIndex {2} \)

Найдите ежемесячный платеж за автомобиль стоимостью 15 000 долларов, если ссуда погашается в течение пяти лет по процентной ставке 9%.

Решение

Два человека, мистер Кэш и мистер Кредит, идут, чтобы купить одну и ту же машину, которая стоит 15 000 долларов. Мистер Кэш платит наличными и уезжает, но мистер Кэш уезжает.Кредит хочет производить ежемесячные выплаты сроком на пять лет.

Наша задача — определить размер ежемесячного платежа. Мы рассуждаем так:

Если г-н Кредит платит m долларов в месяц, то платеж в m долларов, вносимый каждый месяц под 9% на 5 лет, должен дать ту же сумму, что и единовременная выплата в размере 15 000 долларов, депонируемая на 5 лет.

Опять же, мы сравниваем будущие значения для Mr. Cash и Mr. Credit, и мы хотели бы, чтобы они были одинаковыми.

Так как г.{60} -1 \ right]} {. 09/12} \\
\ 15 000 долларов США (1,5657) = m (75,4241) \\
\ 311,38 долларов США = m
\ end {array} \ nonumber \]

Таким образом, ежемесячный платеж, необходимый для погашения ссуды, составляет 311,38 доллара США за пять лет.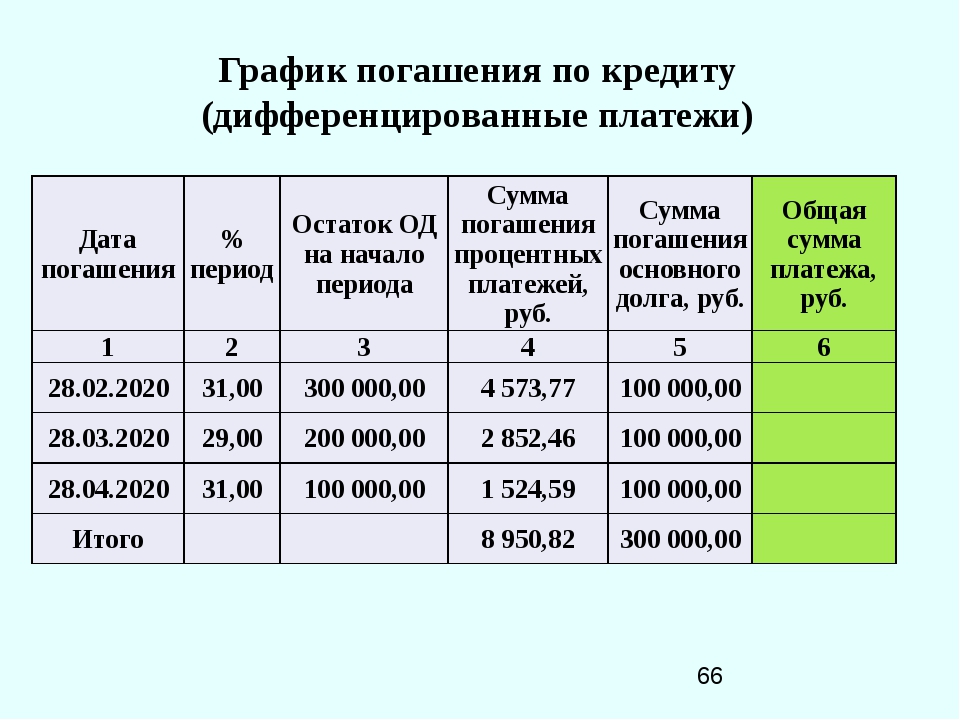 {\ mathrm {nt}} — 1 \ right]} {\ mathrm {r} / \ mathrm {n}} \ label {6.4.1} \]

и решая для текущего значения \ (\ mathrm {P} \) после замены числовых значений для других элементов в формуле, многие учебники сначала решают формулу для \ (\ mathrm {P} \), чтобы разработать новая формула приведенной стоимости. Затем числовая информация может быть подставлена ​​в формулу приведенной стоимости и оценена без необходимости алгебраического решения для \ (\ mathrm {P} \).

Альтернативный метод определения текущей стоимости ренты

Начиная с формулы \ ref {6.{-n t} \ right]} {r / n} \ label {6.4.2} \]

Авторы этой книги считают, что проще использовать формулу \ ref {6.4.1} в верхней части этой страницы и решать для \ (\ mathrm {P} \) или \ (m \) по мере необходимости. При таком подходе нужно понимать меньше формул, и многим студентам легче усваивать. В задачах, оставшихся до конца этой главы, когда проблема требует расчета текущей стоимости аннуитета, будет использоваться формула \ ref {6.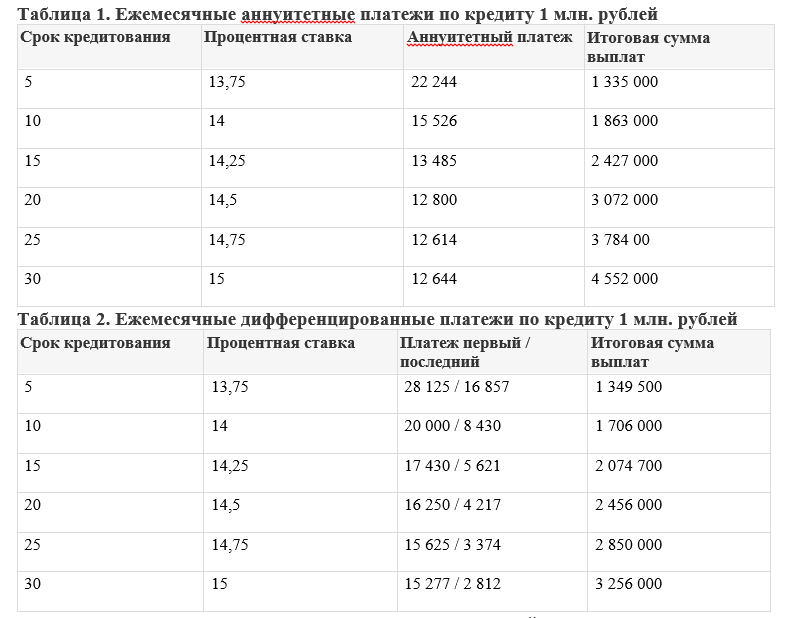 4.1}.

Однако некоторые люди предпочитают формулу \ ref {6.4.2}, и использование этого метода математически корректно. Обратите внимание, что если вы решите использовать формулу \ ref {6.4.2}, вам нужно быть осторожным с отрицательными показателями в формуле. И если вам нужно найти периодический платеж, вам все равно нужно будет выполнить алгебру, чтобы найти значение m.

Было бы неплохо проконсультироваться с вашим инструктором, чтобы узнать, есть ли у него предпочтения. Фактически, вы обычно можете сказать, что предпочитает ваш инструктор, заметив, как он объясняет и демонстрирует эти типы задач в классе.

Аннуитетов

Аннуитет — это фиксированный доход за период времени .

Пример: вы получаете 200 долларов в неделю в течение 10 лет.

Как вы получаете такой доход? Вы покупаете!

Итак:

• вы платите одну большую сумму, затем
• они выплачивают вам обратно серию небольших платежей в течение долгого времени

Пример: вы покупаете аннуитет

Это стоит вам $ 20,000

А взамен вы получаете 400 долларов в месяц на 5 лет

Это хорошая сделка?

Пример (продолжение):

400 долларов в месяц на 5 лет = 400 долларов × 12 × 5 = 24000 долларов

Похоже, хорошая сделка. .. вы получите больше, чем вложили.

Почему вы получаете на больше дохода на (24 000 долларов США) , чем первоначальная стоимость аннуитета (20 000 долларов США) ?

Потому что денег сейчас дороже денег позже.

Люди, получившие ваши 20 000 долларов, могут инвестировать их и получать проценты или делать другие умные вещи, чтобы заработать больше денег.

Итак, сколько должно стоить аннуитета?

Размер аннуитета

Во-первых: давайте посмотрим, как действует процентная ставка в размере 10% (представьте себе банковский счет, который приносит 10% годовых):

Пример: 10% годовых на 1000 долларов

1000 долларов сейчас может заработать 1000 долларов x 10% = 100 долларов в год.

1000 долларов сейчас становится 1100 долларов через год .

Итак, 1100 долларов в следующем году — это те же , что и 1000 долларов сейчас (под 10% годовых).

Приведенная стоимость в размере 1100 долларов в следующем году составит 1000 долларов

Итак, под 10%:

• для перехода с сейчас на в следующем году : умножить на 1,10
• , чтобы перейти с в следующем году на сейчас : разделить на 1.10

Теперь представим аннуитет в размере 4 годовых платежа в размере 500 долларов.

Ваш первый платеж в размере 500 долларов будет в следующем году … сколько это стоит сейчас ?

$ 500 ÷ 1,10 = 454,55 $ сейчас (с точностью до цента)

Ваш второй платеж будет через 2 года. Как это рассчитать? Верните его на один год, затем верните на другой год:

$ 500 ÷ 1,10 ÷ 1,10 = 413,22 $ сейчас

Третий и четвертый платеж также можно вернуть к сегодняшним значениям:

$ 500 ÷ 1.10 ÷ 1.10 ÷ 1.10 = 375.66 $ сейчас

$ 500 ÷ 1,10 ÷ 1,10 ÷ 1,10 ÷ 1,10 = 341,51 $ сейчас

Наконец, складываем 4 платежа (в сегодняшнем значении):

Аннуитетная стоимость = 454,55 долл. США + 413,22 долл. США + 375,66 долл. США + 341,51 долл. США

Аннуитетная стоимость = 1584,94 долларов США

Мы сделали первый расчет аннуитета!

4 ежегодных платежа в размере 500 долларов США под 10% составляют 1584,94 доллара сейчас

Как насчет другого примера:

Пример: аннуитет в размере 400 долларов в месяц в течение 5 лет.

Используйте ежемесячную процентную ставку в размере 1%.

12 месяцев в году, 5 лет, то есть 60 платежей … и МНОГО расчетов.

Нам нужен более простой способ. К счастью, есть отличная формула:

Текущая стоимость аннуитета: PV = P × 1 — (1 + г) ⁻ⁿ r

• P — стоимость каждого платежа
• r — процентная ставка за период в десятичном формате, поэтому 10% равно 0.10
• n — количество периодов

Во-первых, давайте попробуем это на нашем примере за 500 долларов в течение 4 лет.

Годовая процентная ставка составляет 10%, поэтому r = 0,10

Есть 4 платежа, поэтому n = 4 , и каждый платеж составляет 500 долларов, поэтому P = 500 долларов

ЛС = 500 $ × 1 — (1,10) ⁻⁴ 0,10

ЛС = 500 $ × 1-0.68301 … 0,10

ЛС = 500 $ × 3,169865 …

ЛС = 1584,93 долл. США

Соответствует нашему ответу выше (и на 1 цент точнее)

Теперь давайте попробуем это на нашем примере за 400 долларов на 60 месяцев:

Процентная ставка составляет 1% в месяц, поэтому r = 0,01

Есть 60 ежемесячных платежей, поэтому n = 60 , и каждый платеж составляет 400 долларов, поэтому P = 400 долларов

ЛС = 400 $ × 1 — (1.01) ⁻⁶⁰ 0,01

ЛС = 400 $ × 1 — 0,5 5045 … 0,01

ЛС = 400 $ × 44,95504 …

ЛС = 17 982,02 долл. США

Конечно проще, чем 60 отдельных вычислений.

Примечание: используйте процентную ставку за период : для ежемесячных платежей используйте ежемесячную процентную ставку и т. Д.

Другим путем

Что делать, если вы знаете размер аннуитета и хотите рассчитать выплаты?

Допустим, у вас есть 10000 долларов и вы хотите получать ежемесячный доход в течение 6 лет, сколько вы получаете каждый месяц (предположим, что ежемесячная процентная ставка равна 0.5%)

Нам нужно изменить предмет формулы выше

Начать с: PV = P × 1 — (1 + г) ⁻ⁿ r

Поменять местами стороны: P × 1 — (1 + г) ⁻ⁿ r =

Умножаем обе стороны на r : P × (1 — (1 + r) ⁻ⁿ ) = PV × r

Разделим обе части на 1 — (1 + r) ⁻ⁿ : P = PV × г 1 — (1 + г) ⁻ⁿ

И получаем это:

P = PV × г 1 — (1 + г) ⁻ⁿ

• P — стоимость каждого платежа
• PV — текущая стоимость аннуитета
• r — процентная ставка за период в десятичном формате, поэтому 10% равно 0. 10
• n — количество периодов

Допустим, у вас есть 10000 долларов и вы хотите получать ежемесячный доход в течение 6 лет, сколько вы можете получать каждый месяц (предположим, что ежемесячная процентная ставка составляет 0,5%)

Ежемесячная процентная ставка 0,5%, поэтому r = 0,005

Есть 6×12 = 72 ежемесячных платежа, поэтому n = 72 и PV = 10 000 долларов

P = PV × г 1 — (1 + г) ⁻ⁿ

P = 10 000 долл. США × 0.005 1 — (1.005) ⁻⁷²

P = 10 000 долл. США × 0,016572888 …

P = 165,73 долл. США

Что ты предпочитаешь? $ 10,000 сейчас или 6 лет $ 165,73 в месяц

Сноска:

Вам не нужно это запоминать, но вам может быть любопытно, как возникает формула:

При n платежей в размере P и процентной ставке r складывается так:

P × 1 1 + р + P × 1 (1 + г) × (1 + г) + P × 1 (1 + г) × (1 + г) × (1 + г) +. .. (п термины)

Мы можем использовать экспоненты, чтобы помочь. 1 1 + р на самом деле (1 + r) ⁻¹ и 1 (1 + г) × (1 + г) является (1 + r) ⁻² и т. Д .:

P × (1 + r) ⁻¹ + P × (1 + r) ⁻² + P × (1 + r) ⁻³ + … (n членов)

И мы можем поставить букву «П» перед всеми терминами:

P × [(1 + r) ⁻¹ + (1 + r) ⁻² + (1 + r) ⁻³ +… (п термины)]

Еще немного сложнее упростить! Нам нужна умная работа с использованием геометрических последовательностей и сумм b но поверьте мне, это можно сделать … и мы получаем следующее:

PV = P × 1 — (1 + г) ⁻ⁿ r

MyEducator — начисление и дисконтирование аннуитетов

Аннуитет — это равномерно распределенная последовательность равных денежных потоков. Аннуитеты особенно распространены в кредитных отношениях, таких как автокредиты, ипотека и облигации, а также в финансовых договорах, таких как договоры страхования и договоры аренды. Все эти договоренности основаны на равномерно распределенных (например, ежемесячных, ежегодных) платежах одинаковой суммы в долларах. Рисунок 1.3 показывает типичный аннуитет. Обратите внимание, что хотя первый платеж , рис. 1.3, выпадает на момент 1, аннуитеты могут начаться в любой момент времени и продолжаться в течение любого периода времени.Например, поток денежных потоков, показанный на рис. 1.4 , также является аннуитетом, хотя он начинается в момент времени 5 и продолжается до момента 8 (так называемый отсроченный аннуитет).

Рисунок 1.3: Аннуитет с первым платежом в момент 1

Рисунок 1.4: Отсроченный аннуитет

Чтобы рассчитать будущую или текущую стоимость аннуитета, мы можем просто использовать уравнения, приведенные в предыдущем разделе, для сложения или дисконтирования каждого отдельного платежа. Однако при длительных аннуитетах, таких как 30-летняя ипотека с 360 ежемесячными выплатами, это был бы довольно длительный и трудоемкий процесс.Чтобы сократить этот процесс, мы можем вместо этого использовать коэффициент дисконтирования, умноженный на размер аннуитета. Для расчетов будущей стоимости это уравнение:

FV = PMT × {(1 + i) n − 1i}

, где PMT — аннуитетный платеж, n — количество платежей, а две другие переменные, FV и i, определены ранее.

Обратите внимание, что часть уравнения в квадратных скобках определяется исключительно значениями n и i.Этот термин в квадратных скобках иногда называют процентным коэффициентом будущей стоимости аннуитета (FVIFA). Итак, хотя уравнение выглядит более сложным, обратите внимание, что здесь у нас все еще есть только четыре переменных (хотя i появляется дважды в уравнении, каждый раз это одна и та же переменная) и одно уравнение. Следовательно, чтобы найти какую-либо одну переменную, мы должны знать значения трех других. Следовательно, будущая стоимость аннуитета — это игра «3 на 4», точно так же, как расчет настоящей и будущей стоимости для единичных сумм.Следовательно, мы можем использовать наши финансовые калькуляторы для выполнения того же трехэтапного процесса, описанного выше.

Определение приведенной стоимости аннуитета включает аналогичный процесс. Еще раз, у нас есть возможность найти приведенную стоимость каждого отдельного денежного потока в аннуитете и затем суммировать. В качестве альтернативы мы можем использовать следующее уравнение для расчета приведенной стоимости:

PV = PMT × {1− (11 + i) ni}

Часть в квадратных скобках в этом случае называется процентным коэффициентом приведенной стоимости для аннуитета (PVIFA).Концептуально приведенная стоимость аннуитета является сегодняшним скорректированным по времени эквивалентом потока будущих денежных потоков.

Пример: будущая стоимость аннуитета

Давайте посмотрим на пример. Если вы инвестируете 1000 долларов в конце каждого из следующих трех лет под 8%, сколько у вас будет через три года?

Если начиная с сегодняшнего дня, в момент времени 0, мы инвестируем наличные в конце каждого года, наш первый депозит будет в момент времени 1 (в течение одного года), за которым последуют еще два, временами 2 и 3.Если мы зарабатываем 8% от наших вложенных денежных средств, мы хотим знать, сколько всего денег у нас будет в момент 3. Обратите внимание, что время 3 также является моментом, когда мы делаем наш третий и последний депозит — таким образом, концептуально это как если бы мы вносим последнюю тысячу долларов в банк, а затем сразу же спрашиваем у кассира остаток на нашем счете. Этот баланс является будущей стоимостью этого аннуитета и является числом, которое мы хотим вычислить. Как уже упоминалось, мы могли бы рассчитать будущую стоимость, индивидуально сложив каждый из трех денежных потоков, используя уравнение одной суммы, а затем взяв сумму трех отдельных будущих значений.Однако при любом значительном размере аннуитета такая тактика была бы непрактичной и чрезвычайно утомительной. Вместо этого мы можем использовать уравнение аннуитета следующим образом:

FV = 1 000 × {(1 + 0,08) 3−10,08} = 3 246,40 долл. США

Используя финансовый калькулятор в режиме одного платежа в год, мы вводим три известных значения и решаем их будущую стоимость.

Настройка: I = 8

N = 3

PMT = — 1000 долларов США

Решение: FV = 3 246 долларов США.40

Пример: приведенная стоимость аннуитета

Что такое PV в 1000 долларов в конце каждого из следующих трех лет, если альтернативные издержки составляют 8%?

Мы хотим найти текущую стоимость этого потока денежных средств в момент времени 0. Наше уравнение с n = 3, i = 8% и PMT = 1000 долларов дает следующее:

PV = 1000 × {1− (11 + 0.08) 30.08} = 2 577,10

В противном случае мы вводим три известных значения в финансовый калькулятор и решаем для PV:

Настройка: P / Y = 1

I = 8

N = 3

PMT = — 1000 долларов США

Решить: PV = 2 577,10 $

Как мы интерпретируем приведенную стоимость 2 577 долларов.10? Эта стоимость представляет собой сегодняшнюю стоимость трех будущих денежных потоков в 1000 долларов. Предполагая, что у нас действительно 8% альтернативных издержек, нам должно быть безразлично получение трех будущих денежных потоков на конец года в размере 1000 долларов США и 2 577,10 доллара США сегодня. Другой способ интерпретировать приведенную стоимость — представить, что сегодня мы вносим в банк 2 577,10 доллара. Если денежные средства будут расти ежегодно на 8%, мы сможем снимать ровно 1000 долларов каждый год в течение следующих трех лет, не оставляя ничего в банке после третьего вывода.Последним применением приведенной стоимости аннуитета является случай ссуды. Предположим, что сегодня мы занимаем у банка 2 577,10 доллара под 8% на 3 года. Если мы делаем ежегодные платежи, то для погашения кредита до конца третьего года нам придется платить ровно 1000 долларов в год.

Все аннуитеты, которые мы видели в этом разделе, были обычными аннуитетами. Обычный аннуитет имеет задержку в один период между началом периода аннуитета и моментом первого платежа.Например, в нашем предыдущем примере трехлетний аннуитет, начинающийся в момент 0, не производил свой первый платеж до момента 1. Многие потребительские аннуитеты являются обычными. Когда вы подписываете договор о ссуде, например, об автокредите или ипотеке, вы не будете вносить платеж до следующего месяца. Задержка составляет один месяц. При расчете приведенной стоимости обычного аннуитета не забывайте, что вы рассчитываете текущую стоимость за один период до первого денежного потока. Многие студенты здесь, как правило, не справляются с экзаменами по финансам.

Периоды начисления процентов

Если вы зайдете в банк и запросите информацию об автокредите, вам могут сказать что-то вроде «трехлетние ссуды имеют процентную ставку 12% годовых» (годовая процентная ставка означает годовую процентную ставку). Однако, как только вы подадите заявку на получение кредита, вам необходимо будет вносить ежемесячные платежи. Эта разница между частотой выплат и периодом, в течение которого устанавливается процентная ставка, вызывает проблему сложного процента. Если бы мы посчитали выплаты по автокредиту на сумму 10000 долларов США на три года под 12%, у нас может возникнуть соблазн ввести следующие данные:

ЛС = 10 000

N = 3

I / Y = 12

Решить: PMT = — 4 163 долл. США.49

Это, конечно, правильно, если мы хотим рассчитать годовые выплаты. Поскольку кредитный договор предусматривает ежемесячные платежи, расчет годового платежа не подходит. Ключевой момент, который следует помнить в этих сложных задачах, — это то, что все переменные должны быть указаны для одного и того же периода времени. Ранее мы рассчитывали годовые выплаты с использованием годовых процентных ставок — без проблем. Однако теперь нам нужно рассчитать ежемесячные платежи и получить годовую процентную ставку.Чтобы справиться с этим, мы должны скорректировать процентную ставку, чтобы отразить ежемесячный характер выплат. В этом случае мы получаем не трехлетний заем под 12% годовых, а 36-месячный заем (3 года × 12 месяцев в год) со ставкой 1% в месяц (годовая ставка 12%). ÷ 12 месяцев в году). Итак, чтобы рассчитать наши ежемесячные платежи, мы должны ввести в наш финансовый калькулятор следующее:

ЛС = 10 000

N = 3 × 12 = 36

I / Y = 12 ÷ 12 = 1

Решить: pmt = — 332 $.14

Кроме того, обратите внимание, что ежемесячный платеж в размере 332,14 доллара НЕ равен годовому платежу (4 163,49), разделенному на 12, или 346,96 доллара. Почему нет? Потому что, когда вы делаете первый платеж через месяц после предоставления ссуды, часть платежа представляет собой проценты, а часть — основную сумму. Таким образом, в течение второго месяца у вас будет меньший остаток по кредиту, по которому начисляются проценты; это означает, что сумма процентов, начисленных в течение второго месяца, меньше. По сути, ежемесячные платежи, а не ежегодные, сокращают основную сумму быстрее, что приводит к снижению общих процентных расходов, в результате чего ежемесячный платеж оказывается меньше, чем годовой платеж, деленный на 12.

Та же самая логика может применяться к любым различиям во времени между частотой платежей и процентной ставкой. Например, многие бизнес-ссуды включают ежеквартальные платежи (т. Е. Четыре раза в год). Давайте попробуем пример.

Пример: годы до выплаты

Предположим, вы являетесь финансовым директором фирмы, которая взяла взаймы 10 миллионов долларов под 8% (помните, если не указано иное, процентные ставки всегда указываются как годовые).Ежеквартальные выплаты составляют 365 557,48 долларов США. Сколько лет пройдет до погашения кредита?

Решение: Это простая приведенная стоимость задачи аннуитета, когда мы знаем процентную ставку, выплаты и приведенную стоимость, поэтому все, что нам нужно сделать, это вычислить количество периодов, а затем правильно интерпретировать расчет. Следующие нажатия клавиш обеспечивают решение:

ЛС = 10 000 000

I / Y = 8 ÷ 4 = 2 (помните, в году четыре квартала)

PMT = –365,557.48

Решить: N = 40

Толкование: 10 лет до погашения кредита.

Поскольку мы вводили данные (как процентную ставку, так и выплаты) ежеквартально, это решение подразумевает, что ссуда будет погашена в течение 40 кварталов. Однако в исходном вопросе задается количество лет до погашения ссуды. Поскольку в году четыре квартала, мы просто делим 40 на 4, чтобы получить 10 лет.

Возможно, вы заметили, что в приведенном выше упражнении мы ввели платеж как отрицательное число, тогда как в некоторых из наших предыдущих примеров мы проигнорировали знаки движения денежных средств. В этой задаче очень важно следить за приметами. Если вы снова решите проблему и введете как текущую стоимость, так и платеж как положительные числа, ваш калькулятор скажет «Нет решения». Как обсуждалось выше, причина этого в том, что положительный знак указывает на то, что введенная сумма в долларах является притоком.Невозможно получить сегодня приток в размере 10 миллионов долларов, а затем получать приток в размере 365 557,48 долларов каждый квартал без оттока, если только вы не имеете дело с очень необычным банкиром. Следовательно, когда вы вводите несколько долларовых сумм в любую проблему TVM, вам нужно быть осторожным, чтобы решить, какие из них являются притоками, а какие — оттоками. Если введены только две суммы в долларах, обычно не имеет значения, какая из них положительная, а какая отрицательная, если у них разные знаки. Как мы увидим в разделе, посвященном облигациям, когда мы вводим трехдолларовые суммы, отслеживание денежных потоков становится более важным.

Эффективная доходность

Когда вы занимаете деньги в США, федеральный закон требует раскрытия ряда сведений. К ним относятся процентная ставка, срок ссуды, общая сумма процентов, подлежащих выплате, и годовая процентная доходность (APY). В этом контексте APY часто называют эффективной доходностью. Вернитесь к нашему обсуждению сложных процентов в начале этой темы. По сути, мы отметили, что если мы инвестируем в течение нескольких периодов, мы получаем проценты по процентам после первого периода.Что ж, тот же принцип действует, если мы «усложняем» наши процентные платежи, производя более одного платежа в год. Между прочим, та же самая логика является причиной того, что ежемесячные платежи за автомобиль, рассчитанные в предыдущем разделе, были меньше, чем годовые платежи, разделенные на 12.

Чтобы понять эффективную доходность, давайте рассмотрим пример, когда банк предлагает программу сбережений, по которой ежеквартально выплачивается 8% -ная ставка процента. Что именно это означает? По сути, это означает, что после первого квартала вам будут «выплачены» проценты, которые вы заработали к этому моменту (в данном случае 2%).Это, конечно, означает, что проценты, полученные в конце первого квартала, будут приносить проценты за оставшуюся часть года. Точно так же вы получите еще одну выплату процентов в конце второго квартала и так далее. Возможность получать проценты по процентам в течение года — вот что отличает указанную ставку (в данном случае 8% годовых) от эффективной ставки.

Итак, если мы инвестируем в течение одного года по ставке 8% ежеквартально, какова эффективная ставка? Есть два способа подойти к этому вопросу.Во-первых, мы могли бы использовать небольшую алгебру для решения уравнения эффективной ставки, в результате чего получаем

Эффективная доходность = {1 + im} m − 1

где:

i = годовая процентная ставка

м = количество соединений в год

Для нашего примера это дает эффективную ставку

Эффективная доходность = {1 + 0,084} 4−1 = 0.0824 = 8,24%

Следовательно, эти 8% -ные квартальные выплаты дают эффективную доходность 8,24%. Другими словами, если бы вам предлагали 8% комбинированных ежеквартально или 8,24% годовых, вам было бы безразлично, поскольку оба предлагают одинаковую доходность.

Есть другой способ решения этой проблемы. Вместо запоминания формулы вы можете использовать уже изученные навыки TVM и немного интуиции, чтобы получить тот же ответ.Предположим, мы вкладываем 100 долларов на счет, выплачивая 8% начисленных процентов ежеквартально. Сколько у нас будет в конце года? На вашем финансовом калькуляторе это эквивалентно инвестированию на четыре периода (N = 4) под 2% за период, или

PV = –100

N = 4

I / Y = 2

Решить: FV = 108,24 $

Понимая, что это означает, что вложенные сегодня 100 долларов вырастут до 108 долларов.24 через год означает, что эффективная доходность (т. Е. Годовая ставка, которая приведет к росту 100 долларов до 108,24 доллара за один период) в конечном итоге будет следующей:

$$ \ textrm {Эффективная доходность} = (108,24 \ div 100) — 1 = 8,24% $$

Расчет и понимание эффективной доходности — важный навык во многих финансовых ситуациях.

Расчет и понимание эффективной доходности — важный навык во многих финансовых ситуациях.

Хотите попробовать наши встроенные тесты?

Pmt Функция — Доступ

Возвращает значение типа Double, указывающее размер аннуитета, основанный на периодических фиксированных платежах и фиксированной процентной ставке.

Синтаксис

Pmt ( оценка, nper , пв [ , fv ] [ , тип ] )

Синтаксис функции Pmt имеет следующие аргументы:

Замечания

Аннуитет — это серия фиксированных денежных выплат, производимых в течение определенного периода времени. Аннуитет может быть ссудой (например, ипотека на дом) или инвестицией (например, ежемесячным планом сбережений).

Ставка и nper аргументы должны быть рассчитаны с использованием периодов платежей, выраженных в тех же единицах. Например, если ставка рассчитывается с использованием месяцев, nper также необходимо рассчитывать с использованием месяцев.

Для всех аргументов выплаченные денежные средства (например, вклады в сбережения) представлены отрицательными числами; полученные денежные средства (например, чеки на дивиденды) представлены положительными числами.

Пример запроса

Пример VBA

Примечание. Приведенные ниже примеры демонстрируют использование этой функции в модуле Visual Basic для приложений (VBA). Для получения дополнительных сведений о работе с VBA выберите Справочник разработчика в раскрывающемся списке рядом с Поиск и введите один или несколько терминов в поле поиска.

В этом примере используется функция Pmt для возврата ежемесячного платежа по ссуде за фиксированный период.Даны процентная ставка за период (APR / 12), общее количество платежей (TotPmts), приведенная стоимость или основная сумма ссуды (PVal), будущая стоимость ссуды (FVal) и число, указывающее должен ли платеж быть произведен в начале или в конце платежного периода (PayType).

 Dim Fmt, FVal, PVal, APR, TotPmts, PayType, Payment 
 'Когда платежи производятся. 
 Const ENDPERIOD = 0, BEGINPERIOD = 1 
 Fmt = "###, ###, ## 0.00 "'Определите денежный формат. 
 FVal = 0' Обычно 0 для ссуды. 
 PVal = InputBox (" Сколько вы хотите занять? ") 
 APR = InputBox (" Каков годовой "& _ 
" процент ставка вашего кредита? ") 
 Если APR> 1, то APR = APR / 100 'Убедитесь в правильности формы. 
 TotPmts = InputBox (" Сколько ежемесячных "& _ 
" платежей вы сделаете? ") 
 PayType = MsgBox (" Выполняете ли вы платежи «& _ 
» в конце месяца? », VbYesNo) 
 Если PayType = vbNo, то 
 PayType = BEGINPERIOD 
 Else PayType = ENDPERIOD 
 End If 
 Payment = Pmt (APR / 12, TotPmts, -PVal , FVal, PayType) 
 MsgBox "Ваш платеж будет" & _ 
 Format (Payment, Fmt) & "в месяц."
 

будущей стоимости аннуитета | Малый бизнес

Автор Chron Contributor Обновлено 20 октября 2020 г.

Аннуитеты — это инвестиционные контракты, заключенные финансовыми учреждениями, такими как страховые компании и банки. Приобретая аннуитет, вы вкладываете деньги единовременно или постепенно в течение «периода накопления». В указанное время эмитент должен начать регулярные выплаты вам наличными в течение определенного периода времени.”Означает, что N — показатель степени). F — будущая стоимость аннуитета.

Основы аннуитета

Когда вы покупаете аннуитет, эмитент инвестирует ваши деньги для получения дохода. Соглашение представляет собой контракт, который передает риск от физического лица страховой компании или эмитенту аннуитета, сообщает U.S. News. Эмитенты аннуитета зарабатывают деньги, удерживая часть инвестиционного дохода, которая называется ставкой дисконтирования.

Однако по мере того, как вам производится каждый платеж, доход эмитента аннуитета уменьшается.Для эмитента общие затраты на выплату аннуитета равны сумме произведенных вам денежных выплат плюс общее уменьшение дохода, которое эмитент получает по мере совершения платежей. Эмитенты рассчитывают будущую стоимость аннуитетов, чтобы помочь им решить, как планировать выплаты и насколько велика их доля (ставка дисконтирования), чтобы покрыть расходы и получить прибыль.

Формула будущей стоимости аннуитета

Формула будущей стоимости аннуитета незначительно варьируется в зависимости от типа аннуитета.10 — 1) /0.06. Будущая стоимость составит 6 590,40 долларов. Это означает, что по истечении 10 лет общие затраты эмитента составят 6 590,40 долларов (5 000 долларов в виде платежей плюс 1 590,40 долларов в виде невыплаченных процентов).

Периоды выплат

Чтобы использовать уравнение для будущей стоимости аннуитета, когда интервал выплаты составляет менее одного года, необходимо внести две корректировки. Сначала разделите ставку дисконтирования (I) на количество платежей в год, чтобы найти процентную ставку, выплачиваемую каждый месяц.Используйте эту ежемесячную ставку в качестве значения I. Во-вторых, умножьте количество ежегодных платежей (N) на количество платежей каждый год, чтобы найти общее количество платежей, и используйте это значение для N.

Аннуитетный платеж

Поскольку платежи для аннуитета, подлежащего выплате в начале периода выплаты, будущая стоимость аннуитета увеличивается на проценты, полученные за один период времени. Начните с расчета будущей стоимости, используя уравнение для обычной ренты за соответствующий период времени.Затем умножьте результат на 1 + I, где I равно учетной ставке за период.

Формула приведенной стоимости причитающейся аннуитета — AccountingTools

Какова формула приведенной стоимости причитающейся аннуитета?

Текущая стоимость причитающегося аннуитета используется для определения текущей стоимости серии денежных выплат, которые, как ожидается, будут произведены в заранее определенные даты в будущем и в заранее определенных суммах. Расчет обычно производится для того, чтобы решить, следует ли вам получить единовременную выплату сейчас или вместо этого получить серию денежных выплат в будущем (что может быть предложено, если вы выиграете в лотерею).

Расчет приведенной стоимости производится с использованием ставки дисконтирования, которая примерно равна текущей норме прибыли на инвестиции. Чем выше ставка дисконтирования, тем ниже будет приведенная стоимость аннуитета. И наоборот, низкая ставка дисконтирования означает более высокую приведенную стоимость аннуитета.

Формула для расчета приведенной стоимости аннуитета к оплате (когда платежи происходят в начале периода):

P = (PMT [(1 — (1 / (1 + r) n)) / r]) x (1 + r)

Где:

P = текущая стоимость аннуитетного потока, подлежащего выплате в будущем
PMT = сумма каждого аннуитета
r = процентная ставка
n = Количество периодов, в течение которых производятся платежи

Это та же формула, что и для приведенной стоимости обычного аннуитета (где платежи происходят в конце периода), за исключением того, что крайняя правая часть формулы добавляет доплата; это объясняет тот факт, что каждый платеж по существу происходит на один период раньше, чем при обычной модели аннуитета.

Коэффициент, используемый для расчета приведенной стоимости аннуитета, может быть получен из стандартной таблицы коэффициентов приведенной стоимости, в которой соответствующие коэффициенты представлены в матрице по периоду времени и процентной ставке.