| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Оборудование — стандарты, размеры / / Элементы трубопроводов. Фланцы, резьбы, трубы, фитинги…. / / Трубы, трубопроводы. Диаметры труб и другие характеристики. / / Выбор диаметра трубопровода. Скорости потока. Расходы. Прочность. Таблицы выбора, Падение давления. / / Максимальные скорости воды в трубопроводе (трубе) в зависимости от применения принятые в Европе.
| |||||||||||||||||||||||||||||||
| Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||
Вопрос знатокам физики (1) | Не верь стереотипам
Гидравлика. Вопрос о причине снижения манометрического (внутреннего) давления воды при движении по трубе постоянного сечения.
Петр Иванович Дубровский, добросовестный инженер – исследователь, честный и непредвзятый частный научный детектив.
Итак, смотрим видео:
Сделаем стоп-кадр:
Пояснения и объяснения преподавателя (курсив, лишние фразы не воспроизвожу, но дополняю — plain text):
Вы видите, что чем ближе к входу, тем выше уровень воды в манометрических трубках. Соответственно, тем больше давление воды в этом сечении.
Соответственно, тем больше давление воды в этом сечении.
В чём причина?
Дело в том, что, когда течёт вода по трубе, то при этом существует трение между водой и поверхностью трубы, а также между отдельными слоями воды.В центре трубы вода течёт с большей скоростью, чем рядом с трубой, где, по утверждению преподавателя, скорость воды равна нулю. Не знаю, откуда он почерпнул такие потрясающие познания про нулевую скорость, мне трудно бороться с буйным полётом фантазии многих физико-теоретиков, но допустим, что непосредственно у трубы скорость потока равна нулю, хотя на самом деле это определяется шероховатостью внутренней поверхности трубы и, что немаловажно — смачиваемостью материала, из которого изготовлена труба.
Вот, в текущей жидкости совершается работа против сил трения и поэтому кинетическая энергия (видимо, кинетическая энергия потока, состоящая из суммы кинетических энергий всех молекул воды, задействованных в потоке) будет тем меньше, чем ближе мы будем находиться (видимо, чем ближе то или иное сечение трубы) к сливному отверстию.
Ага, вон оно как, оказывается. Правда, после этого я внезапно услышал более-менее здравые слова: По мере приближения к сливному отверстию уменьшается напор жидкости, уменьшается и давление в жидкости.
А теперь давайте не спеша разбираться в том, что именно наговорил этот чудик физико-педагог.
Итак, величина потока, как принято считать, в трубе постоянного диаметра постоянная — то есть за один и тот же интервал через разные сечения трубы (в начале трубы, в середине в конце) проходит одинаковое количество молекул воды.
Так вот, я, как человек, слегка знакомый с гидравликой и занимавшийся испытаниями машин и механизмов, которые работали на гидравлическом приводе, а также, как инженер-мостовик — с распределением скоростей течения потока в реках по глубине и при сужении и расширении русла, с размывом грунта у свайных фундаментов при сооружении опор в русле, что отрицает «нулевую скорость течения», то есть я не по-наслышке знаком с реальной гидравликой, я хотел бы задать этому горе-физику несколько вопросов. 2/2 тоже потрясающим, невероятным образом увеличивается — без какого-либо дополнительного воздействия извне. А это, други мои, позволяет призадуматься тем гражданам, которые истово веруют в энергию, выдуманную Лейбницем и в нынешний закон сохранения энергии, над созданием вечного двигателя.
2/2 тоже потрясающим, невероятным образом увеличивается — без какого-либо дополнительного воздействия извне. А это, други мои, позволяет призадуматься тем гражданам, которые истово веруют в энергию, выдуманную Лейбницем и в нынешний закон сохранения энергии, над созданием вечного двигателя.
Смотрим. Уменьшение диаметра трубы в 2 раза приводит к увеличению скорости молекул (при постоянстве величины потока) аж в 4 раза. Таким образом, не напрягаясь и без каких-либо затрат можно увеличить кинетическую энергию имени Лейбница аж в 16 раз. Каково? Тем, кому этого мало, может уменьшить диаметр трубы в 5 раз. Скорость молекул увеличится тогда в 25 раз, а кинетическая энергия имени Лейбница — невероятно, причем без каких-либо затрат — в 625 раз. Затем адептам энергии имени Лейбница останется лишь придумать, как лучше реализовать эту дармовую кинетическую энергию. Пускай даже КПД устройства для этой реализации будет всего 10%, но при уменьшении диаметра трубы в 5 раз всё равно можно будет получить более чем 60-кратную дармовщинку.
Так что, верующие в непогрешимость и гений РАН, профессоров вузов и Министерств просвещения, высшего образования и науки — дерзайте. Дармовая энергия прямо под вашим носом — так возьмите её.
А я, бедолага, лучше этим заниматься не стану, так как уже уяснил для себя дебилизм кое-каких общепризнанных догматов. И поэтому я сейчас просто ищу АДЕКВАТНОЕ ИЗДАТЕЛЬСТВО для ЗАДУМАННОЙ МНОЙ КНИГИ.
Эта статья, как планируется, может стать одной из глав этой книги, одной из демонстраций глупости нынешнего закона сохранения энергии.
Ну а по поводу истинных причин падения давления в трубе постоянного сечения я бы хотел услышать тех, кто считает себя физиком-профессионалом.
Да, забыл предупредить: тупые посты малограмотных остолопов буду стирать не задумываясь. Если Вы написали пост и потом не увидели его, это означает лишь одно — Вам следует вновь вернуться к школьным учебникам физики, рекомендую «Элементарный учебник физики» под редакцией академика Г. С. Ландсберга. Но при этом не надо слепо и безоговорочно верить всему, что там написано.
С. Ландсберга. Но при этом не надо слепо и безоговорочно верить всему, что там написано.
Закон Бернулли : Помогите решить / разобраться (Ф)
Скорость потока частично гасится на заслонке.
Если сечение трубы остаётся после крана тем же самым, то и скорость потока после крана неизменно будет равна скорости потока до крана. Потому что поток воды сохраняется. А гасится не скорость, а энергия, переносимая потоком воды в трубе в единицу времени, и, соответственно, давление. До крана поток энергии в трубе оказывается выше, чем после крана.
В сплошной среде, такой, как жидкость, поток энергии связан не только с переносом кинетической или потенциальной энергии частиц среды, но часть потока энергии также связана с работой сил давления при перемещении среды. Рассмотрите немного другой пример из механики. Вы поднимаете тяжелое ведро при помощи верёвки. Скорость ведра постоянна, его кинетическая энергия не изменяется. Но ведро поднимается вверх, значит, его потенциальная энергия возрастает. Откуда берётся эта энергия? Она передаётся ведру от ваших мышц, совершающих работу. Но как она передаётся ведру, если вы тянете только за верёвку? Она передаётся при перемещении натянутой верёвку. И она не связана ни с кинетической, ни с потенциальной энергией верёвки, так как верёвка очень лёгкая. А энергия от ваших мышц передаётся ведру при перемещении этой натянутой верёвки как работа силы натяжения верёвки.
Точно так же и в трубе. Поток воды, кроме кинетической и потенциальной энергии переносимой воды, также, переносит часть энергии вдоль трубы за счёт работы сил давления. Изначально эта энергия поставляется в трубу насосом, создающим давление. Частично эта энергия расходуется на подъём воды от насоса до уровня потребителя, т. е. вашего крана, частично она расходуется на преодоление вязкостных потерь в трубах. Но всё, что осталось, оно вам не нужно, так как вам из крана нужен спокойный поток воды, который будет течь без разбрызгивания. И избыток переносимой водой в трубе энергии вы гасите в кране, который снижает давление и, следовательно, энергию вытекающей из крана воды до приемлемого для вас уровня.
Уравнение Бернулли — это закон сохранения энергии для потока воды, в котором игнорируются потери. Оно применимо для эжекторов, которые проектируются таким образом, чтобы минимизировать потери энергии в них. Но оно неприменимо для кранов, так как краны — это устройства, которые гасят избыточную энергию потока, попутно регулируя поток вытекающей у потребителя воды.
Гидроудар в трубе — причины, защита, компенсаторы
Защита от гидроудара
Чтобы защитить трубопровод от гидравлических ударов, нужно:
- Плавно открывать/закрывать запорные элементы
При плавном закрывании крана давление в трубопроводе будет постепенно выравниваться. При этом ударная волна будет иметь незначительную силу, а следовательно, мощность гидравлического удара будет минимальной. Но не во всех случаях возможно обеспечить плавное закрывание крана. Далеко не у всех моделей вентильная конструкция, многие современные краны имеют шаровую систему – достаточно одного неосторожного резкого поворота и кран придёт в положение «закрыто».
- Использовать трубы большого диаметра
В трубопроводах большого диаметра рабочая среда движется с меньшей скоростью, чем в системах с более маленьким диаметром. А чем скорость перемещения потока жидкости меньше, тем слабее сила гидроудара. Однако данный способ гораздо затратнее. Расходы увеличиваются за счёт более высокой стоимости труб и теплоизоляции.
- Установить амортизирующее устройство
Данное устройство располагается по направлению движения рабочей жидкости. В качестве амортизатора используется отрезок трубы из эластичного пластик либо каучука, которым заменяется часть жёсткой трубы перед термостатом. При возникновении гидравлического удара происходит растяжение эластичного отрезка и частичное гашение силы удара.
- Использовать компенсаторное оборудование
Для сбрасывания лишней жидкости до момента нормализации давления в трубопроводе используется гидравлический аккумулятор.
- Использовать автоматику насосов
Одной из причин появления гидравлических ударов в трубопроводе является насосное оборудование. Движение рабочей среды зависит от того, насколько быстро вращаются насосные валы. Следовательно, плавное снижение/увеличение скорости вращения позволяет уменьшить силу воздействия и снизить риск появления гидроударов.
На производствах для управления насосным оборудованием используются специальные регуляторы, частотные преобразователи и прочие подобные приборы. Данное оборудование также подходит для использования в бытовых условиях.
Гидравлические удары в коммуникациях появляются при остановке насосного оборудования, например, при исчезновении сети питания. На производствах и в сфере коммунального хозяйства резервные источники используются давно и не раз доказали свою эффективность. Предупреждение аварийных ситуаций и сокращение расходов на ремонтные работы приводят к существенной экономии средств. Включение домашнего насосного оборудования через устройство защиты от гидроударов (стабилизаторы и источники резервного питания) поможет обезопасить внутренние коммуникационные системы.
- Использовать байпас
Байпас представляет собой дополнительный участок трубопровода, который используется в качестве обходного канала и служит для регулирования пропускной способности сети отопления. Такие устройства можно монтировать, как в новые системы, так и в уже существующие.
- Гаситель гидроударов
Это простое, но эффективное изобретение, работающее по принципу расширительного бака отопительных коммуникаций. При резком перепаде давления жидкость перемещается в мембранный гаситель. После того, как давление в трубопроводе упадёт до рабочей величины, произойдёт выталкивание жидкости обратно в систему.
- Защитный клапан
Клапан защиты от гидроудара располагается в трубопроводной системе рядом с наносом. Он реагирует на скачки давления, принимая обратную волну и предотвращая гидравлические удары. Клапан оснащён специальным регулятором, который при перепаде давления плавно открывает его. Таким образом, когда обратный поток рабочей среды доходит до насосного агрегата, клапан уже находится в открытом состоянии. В результате этого происходит сбрасывание воды, а следовательно, снижение давления до допустимой величины. После нормализации давления регулятор закрывает клапан, чтобы предотвратить опустошение системы.
аэродинамика — Как давление жидкости изменяется в зависимости от площади в соответствии с уравнением неразрывности и уравнением Бернулли?
Я не согласен с ответом, получившим наибольшее количество голосов от CAGT. Он говорит «Эта область полностью отличается от той, что указана выше» , но это ничего не значит. Упомянутое автором уравнение $ p = {F \ over A} $ действительно выполняется, и в нем нет противоречия или парадокса.
Фактически, уравнение $ p = {F \ over A} $ выполняется не только здесь, но и везде в физике.2 \ более 2} + gz = \ text {constant} $$
Итак, ваша проблема связана с $ p = {F \ over A} $. Что ж, с этим проблем нет. Что на самом деле
Давайте вспомним, что происходит в вашей ситуации:
- Произошло изменение площади поперечного сечения: $ A_2
- Благодаря сохранению массы , (1) подразумевает $ v_2> v_1 $
- Благодаря Бернулли , (2) подразумевает $ p_2
Хорошо, теперь посмотрим на это.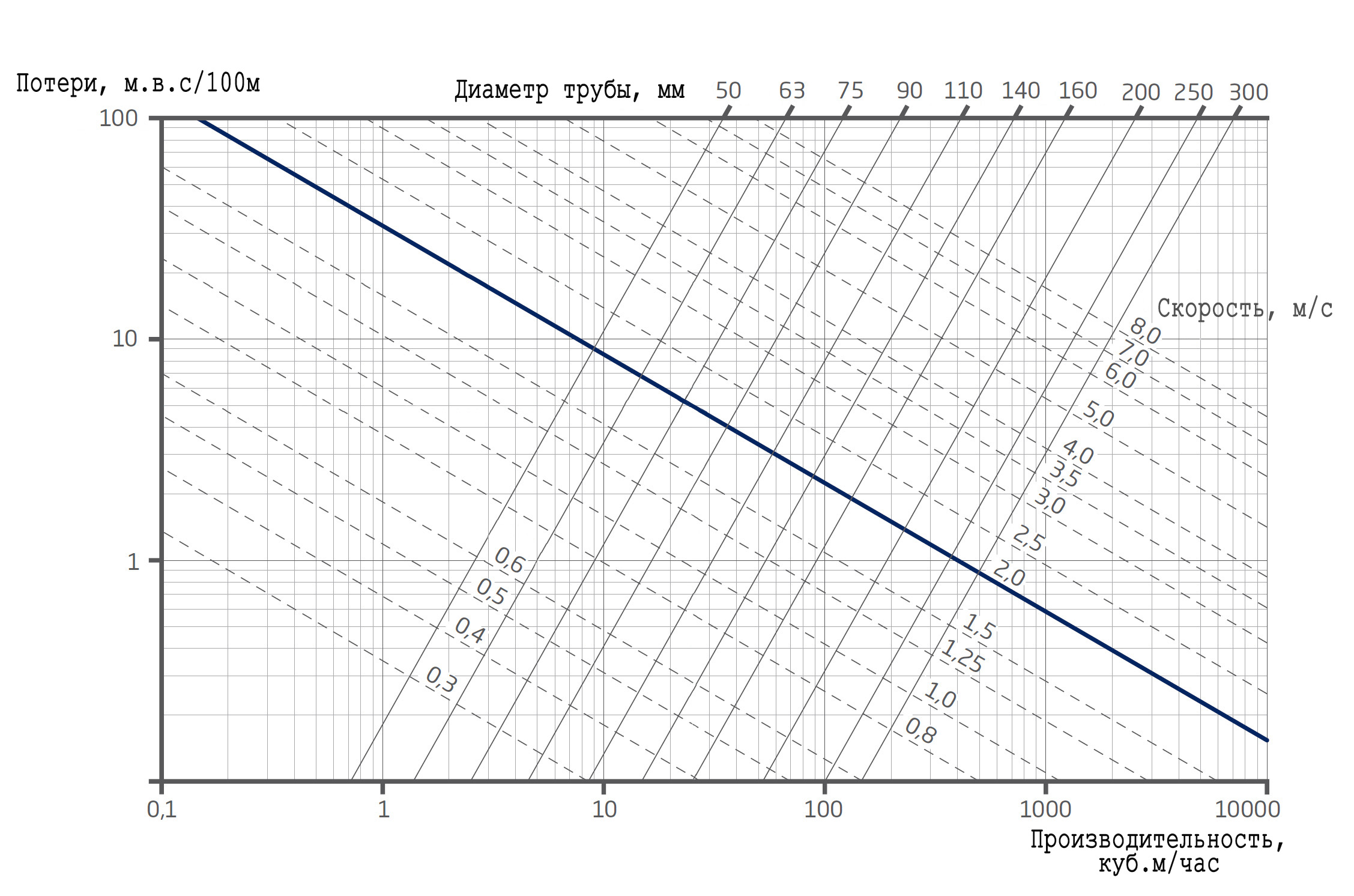
Темно-синий прямоугольник слева — это то, что мы называем элементом
Теперь перейдем к элементу меньшего участка, который течет быстрее. Площадь его поперечного сечения меньше.Давление слева и справа также меньше. В результате сжимающие его силы, $ F_2 = p_2 A_2 $, также меньше.
Итак, $ p = {F \ over A} $ по-прежнему выполняется. Да, когда ситуация изменится, $ A $ станет меньше, что само по себе сделало бы $ p $ больше. Однако, как мы видели выше, новый $ F $ тоже меньше старого, что само по себе сделало бы $ p $ меньше. Чистый эффект от $ p_2 К концу этого раздела вы сможете: вязкость и ламинарный поток; Закон Пуазейля
Цели обучения
Ламинарный поток и вязкость
Когда вы наливаете себе стакан сока, жидкость течет свободно и быстро.Но когда вы поливаете блины сиропом, эта жидкость медленно течет и прилипает к кувшину. Разница заключается в трении жидкости как внутри самой жидкости, так и между жидкостью и окружающей средой. Мы называем это свойство жидкостей вязкостью . Сок имеет низкую вязкость, тогда как сироп имеет высокую вязкость. В предыдущих разделах мы рассматривали идеальные жидкости с небольшой вязкостью или без нее. В этом разделе мы исследуем, какие факторы, включая вязкость, влияют на скорость потока жидкости. Точное определение вязкости основано на ламинарном или нетурбулентном потоке. Прежде чем мы сможем определить вязкость, нам нужно определить ламинарный поток и турбулентный поток. На рисунке 1 показаны оба типа потока. Ламинарный поток характеризуется плавным течением жидкости слоями, которые не смешиваются. Турбулентный поток, или турбулентность , характеризуется завихрениями и завихрениями, которые смешивают слои жидкости вместе.
Точное определение вязкости основано на ламинарном или нетурбулентном потоке. Прежде чем мы сможем определить вязкость, нам нужно определить ламинарный поток и турбулентный поток. На рисунке 1 показаны оба типа потока. Ламинарный поток характеризуется плавным течением жидкости слоями, которые не смешиваются. Турбулентный поток, или турбулентность , характеризуется завихрениями и завихрениями, которые смешивают слои жидкости вместе.
Рис. 1. Дым плавно поднимается на некоторое время, а затем начинает образовывать завихрения и водовороты.Плавный поток называется ламинарным потоком, тогда как завихрения и водовороты типичны для турбулентного потока. Если вы посмотрите на дым (стараясь не дышать на него), вы заметите, что при плавном течении он поднимается быстрее, чем после того, как он становится турбулентным, что означает, что турбулентность оказывает большее сопротивление потоку. (кредит: Creativity103)
На рис. 2 схематически показано, чем отличаются ламинарный и турбулентный потоки. Слои текут без перемешивания, когда поток ламинарный. Когда есть турбулентность, слои перемешиваются, и есть значительные скорости в направлениях, отличных от общего направления потока.Линии, показанные на многих иллюстрациях, представляют собой пути, по которым проходят небольшие объемы жидкости. Эти линии называются . Линии тока плавные и непрерывные, когда поток является ламинарным, но разделяются и перемешиваются, когда поток является турбулентным. У турбулентности есть две основные причины. Во-первых, любое препятствие или острый угол, например, в кране, создает турбулентность, сообщая скорости, перпендикулярные потоку. Во-вторых, высокие скорости вызывают турбулентность. Сопротивление как между соседними слоями жидкости, так и между жидкостью и окружающей средой образует завихрения и водовороты, если скорость достаточно велика.В оставшейся части этого раздела мы сконцентрируемся на ламинарном потоке, оставив некоторые аспекты турбулентности для последующих разделов.
Рис. 2. (a) Ламинарное течение происходит слоями без перемешивания. Обратите внимание, что вязкость вызывает сопротивление между слоями, а также с неподвижной поверхностью. (b) Препятствие в судне вызывает турбулентность. Турбулентный поток перемешивает жидкость. Здесь больше взаимодействия, больше нагрева и больше сопротивления, чем в ламинарном потоке.
Установление соединений: эксперимент на вынос: спуститься к рекеПопробуйте одновременно бросить две палки в текущую реку: одну у края реки, а другую — у середины.Какой из них путешествует быстрее? Почему?
На рисунке 3 показано, как измеряется вязкость жидкости. Между двумя параллельными пластинами находится определенная жидкость. Нижняя пластина зафиксирована, а верхняя пластина перемещается вправо, увлекая за собой жидкость. Слой (или пластинка) жидкости, контактирующий с любой пластиной, не перемещается относительно пластины, поэтому верхний слой перемещается со скоростью v , в то время как нижний слой остается в покое. Каждый последующий слой сверху вниз оказывает силу на слой под ним, пытаясь увлечь его, создавая непрерывное изменение скорости от v до 0, как показано.Необходимо следить за тем, чтобы поток был ламинарным; то есть слои не смешиваются. Движение на Рисунке 3 похоже на непрерывное режущее движение. Жидкости имеют нулевую прочность на сдвиг, но скорость , с которой они сдвигаются, связана с теми же геометрическими факторами A и L , как и деформация сдвига для твердых тел.
Рис. 3. На графике показан ламинарный поток жидкости между двумя пластинами области A. Нижняя пластина закреплена. Когда верхняя пластина сдвигается вправо, она увлекает за собой жидкость.
Сила F требуется, чтобы верхняя пластина на Рисунке 3 двигалась с постоянной скоростью v , и эксперименты показали, что эта сила зависит от четырех факторов. Во-первых, F прямо пропорционально v (пока скорость не станет настолько высокой, что возникает турбулентность — тогда требуется гораздо большая сила, и она имеет более сложную зависимость от v ). Во-вторых, F пропорционально площади A пластины.Это соотношение кажется разумным, поскольку A прямо пропорционально количеству перемещаемой жидкости. В-третьих, F обратно пропорционально расстоянию между пластинами L . Эти отношения также разумны; L похож на плечо рычага, и чем больше плечо рычага, тем меньше силы требуется. В-четвертых, F прямо пропорционально коэффициенту вязкости , η .Чем больше вязкость, тем больше требуется сила. Эти зависимости объединены в уравнение
Во-первых, F прямо пропорционально v (пока скорость не станет настолько высокой, что возникает турбулентность — тогда требуется гораздо большая сила, и она имеет более сложную зависимость от v ). Во-вторых, F пропорционально площади A пластины.Это соотношение кажется разумным, поскольку A прямо пропорционально количеству перемещаемой жидкости. В-третьих, F обратно пропорционально расстоянию между пластинами L . Эти отношения также разумны; L похож на плечо рычага, и чем больше плечо рычага, тем меньше силы требуется. В-четвертых, F прямо пропорционально коэффициенту вязкости , η .Чем больше вязкость, тем больше требуется сила. Эти зависимости объединены в уравнение
[латекс] F = \ eta \ frac {{vA}} {L} \\ [/ latex],
, что дает нам рабочее определение вязкости жидкости η . Решение относительно η дает
[латекс] \ eta = \ frac {FL} {vA} \\ [/ latex],
, который определяет вязкость с точки зрения ее измерения. Единица вязкости в системе СИ: Н · м / [(м / с) м 2 ] = (Н / м 2 ) с или Па · с.В таблице 1 приведены коэффициенты вязкости для различных жидкостей.
Вязкость варьируется от одной жидкости к другой на несколько порядков. Как и следовало ожидать, вязкость газов намного меньше вязкости жидкостей, и эта вязкость часто зависит от температуры. Вязкость крови можно снизить, употребляя аспирин, что позволяет ему легче циркулировать по телу. (При длительном применении в низких дозах аспирин может помочь предотвратить сердечные приступы и снизить риск свертывания крови.)
| Жидкость | Температура (ºC) | Вязкость η (мПа · с) |
|---|---|---|
| Газы | ||
| Воздух | 0 | 0,0171 |
| 20 | 0,0181 | |
| 40 | 0,0190 | |
| 100 | 0,0218 | |
| Аммиак | 20 | 0. 00974 00974 |
| Двуокись углерода | 20 | 0,0147 |
| Гелий | 20 | 0,0196 |
| Водород | 0 | 0,0090 |
| Меркурий | 20 | 0,0450 |
| Кислород | 20 | 0,0203 |
| Пар | 100 | 0,0130 |
| Жидкости | ||
| Вода | 0 | 1.792 |
| 20 | 1,002 | |
| 37 | 0,6947 | |
| 40 | 0,653 | |
| 100 | 0,282 | |
| Цельная кровь | 20 | 3,015 |
| 37 | 2,084 | |
| Плазма крови | 20 | 1,810 |
| 37 | 1,257 | |
| Этиловый спирт | 20 | 1.20 |
| Метанол | 20 | 0,584 |
| Масло (тяжелая машина) | 20 | 660 |
| Масло (моторное, SAE 10) | 30 | 200 |
| Масло (оливковое) | 20 | 138 |
| Глицерин | 20 | 1500 |
| Мед | 20 | 2000–10000 |
| Кленовый сироп | 20 | 2000–3000 |
| Молоко | 20 | 3.0 |
| Масло (Кукурузное) | 20 | 65 |
Ламинарный поток, ограниченный трубками — закон Пуазейля
Что вызывает поток? Ответ, что неудивительно, — разница в давлении. Фактически, существует очень простая взаимосвязь между горизонтальным потоком и давлением. Расход Q находится в направлении от высокого давления к низкому. Чем больше перепад давления между двумя точками, тем больше расход.Это отношение может быть указано как
Чем больше перепад давления между двумя точками, тем больше расход.Это отношение может быть указано как
[латекс] Q = \ frac {{P} _ {2} — {P} _ {1}} {R} \\ [/ latex],
, где P 1 и P 2 — это давления в двух точках, например, на обоих концах трубы, а R — сопротивление потоку. Сопротивление R включает все, кроме давления, которое влияет на скорость потока. Например, R больше для длинной трубки, чем для короткой.Чем больше вязкость жидкости, тем больше значение R . Турбулентность сильно увеличивается R , тогда как увеличение диаметра трубы уменьшает R . Если вязкость равна нулю, жидкость не имеет трения, и сопротивление потоку также равно нулю. Сравнивая поток без трения в трубе с вязким потоком, как показано на рисунке 4, мы видим, что для вязкой жидкости скорость максимальна в середине потока из-за сопротивления на границах. Мы можем видеть эффект вязкости в пламени горелки Бунзена, даже если вязкость природного газа мала.{4}} \\ [/ латекс].
Это уравнение называется закон Пуазейля для сопротивления в честь французского ученого Ж. Л. Пуазейля (1799–1869), который вывел его в попытке понять поток крови, часто турбулентной жидкости.
Рис. 4. (a) Если поток жидкости в трубке имеет незначительное сопротивление, скорость по всей трубке одинакова. (b) Когда вязкая жидкость течет через трубку, ее скорость у стенок равна нулю, постоянно увеличиваясь до максимума в центре трубки.(c) Форма пламени горелки Бунзена обусловлена профилем скорости в трубе. (кредит: Джейсон Вудхед)
Давайте исследуем выражение Пуазейля для R , чтобы увидеть, имеет ли оно хороший интуитивный смысл. Мы видим, что сопротивление прямо пропорционально вязкости жидкости η и длине трубки л . В конце концов, оба эти фактора напрямую влияют на величину возникающего трения — чем оно больше, тем больше сопротивление и меньше поток.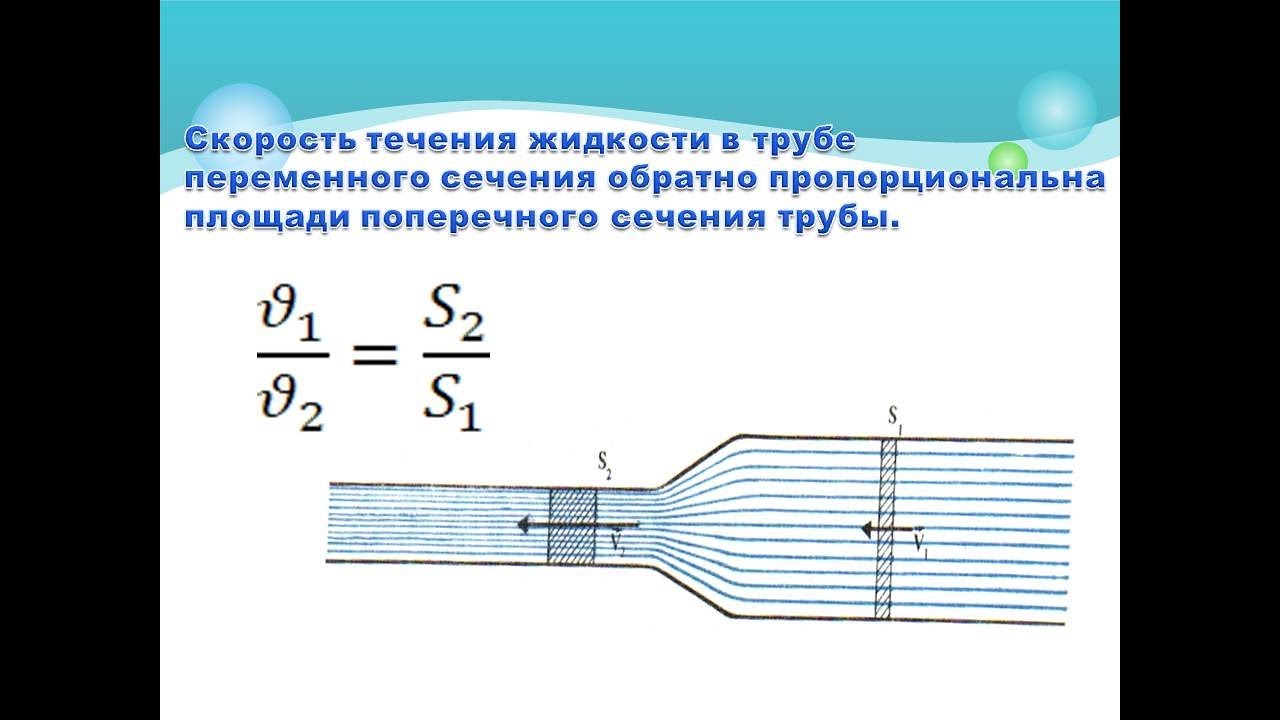 {4}} {8 \ eta l} \\ [/ latex] .{4} \\ [/ латекс].
{4}} {8 \ eta l} \\ [/ latex] .{4} \\ [/ латекс].
Следовательно, r 2 = (0,5) 0,25 r 1 = 0,841 r 1 , уменьшение радиуса артерии на 16%.
ОбсуждениеЭто уменьшение радиуса на удивление мало для данной ситуации. Для восстановления кровотока, несмотря на это накопление, потребуется увеличение разницы давлений ( P 2 — P 1 ) в два раза с последующей нагрузкой на сердце.
Система кровообращения дает множество примеров действия закона Пуазейля — кровоток регулируется изменениями размера сосудов и кровяного давления. Кровеносные сосуды не жесткие, а эластичные. Регулировка кровотока в основном осуществляется путем изменения размера сосудов, поскольку сопротивление очень чувствительно к радиусу. Во время интенсивных упражнений кровеносные сосуды выборочно расширяются до важных мышц и органов, и повышается кровяное давление. Это создает как больший общий кровоток, так и повышенный приток к определенным областям.И наоборот, уменьшение радиуса сосудов, возможно, из-за бляшек в артериях, может значительно уменьшить кровоток. Если радиус судна уменьшается всего на 5% (до 0,95 от исходного значения), расход уменьшается примерно до (0,95) 4 = 0,81 от исходного значения. Уменьшение расхода на 19% вызвано уменьшением радиуса на 5%. Организм может компенсировать это повышением артериального давления на 19%, но это представляет опасность для сердца и любых сосудов с ослабленными стенками. Другой пример — автомобильное моторное масло.Если у вас есть автомобиль с манометром масла, вы можете заметить, что давление масла высокое, когда двигатель холодный. Вязкость моторного масла в холодном состоянии выше, чем в теплом, поэтому давление должно быть выше, чтобы перекачивать такое же количество холодного масла.
Рис. 5. Закон Пуазейля применяется к ламинарному течению несжимаемой жидкости с вязкостью η через трубку длиной l и радиусом r. Направление потока — от большего к меньшему давлению. Расход Q прямо пропорционален разности давлений P 2 — P 1 и обратно пропорционален длине l трубки и вязкости η жидкости.Расход увеличивается с r 4 , четвертой степени радиуса.
Направление потока — от большего к меньшему давлению. Расход Q прямо пропорционален разности давлений P 2 — P 1 и обратно пропорционален длине l трубки и вязкости η жидкости.Расход увеличивается с r 4 , четвертой степени радиуса.
Пример 2. Какое давление создает этот расход?
Внутривенная (IV) система подает физиологический раствор пациенту со скоростью 0,120 см 3 / с через иглу радиусом 0,150 мм и длиной 2,50 см. Какое давление необходимо на входе иглы, чтобы вызвать этот поток, если считать, что вязкость физиологического раствора такая же, как у воды? Манометрическое давление крови в вене пациента — 8.{2} \ end {array} \\ [/ latex].
Обсуждение
Это давление может быть обеспечено с помощью баллона для внутривенного вливания с поверхностью физиологического раствора на 1,61 м над входом в иглу (это оставлено вам для решения в Задачах и упражнениях этой главы), при условии, что перепад давления в игле пренебрежимо мал. трубка, ведущая к игле.
Поток и сопротивление как причины падений давления
Возможно, вы заметили, что давление воды в вашем доме может быть ниже обычного в жаркие летние дни, когда больше используется.Это падение давления происходит в водопроводе еще до того, как оно достигнет вашего дома. Давайте рассмотрим поток через водопровод, как показано на рисунке 6. Мы можем понять, почему давление в доме P 1 падает во время интенсивного использования, переставив
[латекс] Q = \ frac {{P} _ {2} — {P} _ {1}} {R} \\ [/ latex]
Спо
[латекс] {P} _ {2} — {P} _ {1} = RQ \\ [/ latex],
, где в данном случае P 2 — давление на водопроводной станции, а R — сопротивление водопровода.Во время интенсивного использования расход Q велик. Это означает, что P 2 — P 1 также должны быть большими. Таким образом, P 1 должно уменьшиться. Правильно считать, что поток и сопротивление вызывают падение давления с P 2 до P 1 . P 2 — P 1 = RQ действительно как для ламинарных, так и для турбулентных потоков.
Это означает, что P 2 — P 1 также должны быть большими. Таким образом, P 1 должно уменьшиться. Правильно считать, что поток и сопротивление вызывают падение давления с P 2 до P 1 . P 2 — P 1 = RQ действительно как для ламинарных, так и для турбулентных потоков.
Рис. 6. Во время интенсивного использования в водопроводе наблюдается значительный перепад давления, и P 1 , подаваемое пользователям, значительно меньше, чем P 2 , созданное на гидротехнических сооружениях. Если расход очень мал, перепад давления незначителен, и P 2 ≈ P 1 .
Мы можем использовать P 2 — P 1 = RQ для анализа перепадов давления, возникающих в более сложных системах, в которых радиус трубы не везде одинаков.Сопротивление будет намного выше в узких местах, таких как закупорка коронарной артерии. Для заданного расхода Q перепад давления будет наибольшим там, где труба наиболее узкая. Так водопроводные краны управляют потоком. Кроме того, R сильно увеличивается из-за турбулентности, а сужение, которое создает турбулентность, значительно снижает давление ниже по потоку. Зубной налет в артерии снижает давление и, следовательно, поток, как за счет сопротивления, так и за счет создаваемой турбулентности.
На рисунке 7 схематически изображена кровеносная система человека, показывающая среднее артериальное давление в ее основных частях для взрослого человека в состоянии покоя. Давление, создаваемое двумя насосами сердца, правым и левым желудочками, снижается за счет сопротивления кровеносных сосудов, когда кровь течет через них. Левый желудочек увеличивает артериальное давление, что приводит к току крови через все части тела, кроме легких. Правый желудочек получает кровь с более низким давлением из двух основных вен и перекачивает ее через легкие для газообмена с атмосферными газами — удаления углекислого газа из крови и пополнения запасов кислорода.Схематически показан только один крупный орган с типичным разветвлением артерий на все более мелкие сосуды, самые маленькие из которых являются капиллярами, и соединением мелких вен с более крупными. Подобное разветвление происходит во множестве органов тела, и система кровообращения обладает значительной гибкостью в регулировании потока к этим органам за счет расширения и сужения артерий, ведущих к ним, и капилляров внутри них. Чувствительность потока к радиусу трубки делает эту гибкость возможной в большом диапазоне скоростей потока.
Правый желудочек получает кровь с более низким давлением из двух основных вен и перекачивает ее через легкие для газообмена с атмосферными газами — удаления углекислого газа из крови и пополнения запасов кислорода.Схематически показан только один крупный орган с типичным разветвлением артерий на все более мелкие сосуды, самые маленькие из которых являются капиллярами, и соединением мелких вен с более крупными. Подобное разветвление происходит во множестве органов тела, и система кровообращения обладает значительной гибкостью в регулировании потока к этим органам за счет расширения и сужения артерий, ведущих к ним, и капилляров внутри них. Чувствительность потока к радиусу трубки делает эту гибкость возможной в большом диапазоне скоростей потока.
Рисунок 7. Схема кровеносной системы. Перепад давления создается двумя насосами в сердце и уменьшается за счет сопротивления сосудов. Разветвление сосудов в капилляры позволяет крови достигать отдельных клеток и обмениваться с ними веществами, такими как кислород и продукты жизнедеятельности. Система обладает впечатляющей способностью регулировать поток к отдельным органам, в основном за счет изменения диаметра сосудов.
Каждое разветвление более крупных сосудов на более мелкие увеличивает общую площадь поперечного сечения трубок, по которым течет кровь.Например, артерия с поперечным сечением 1 см 2 может разветвляться на 20 меньших артерий, каждая с поперечным сечением 0,5 см 2 , всего 10 см 2 . Таким образом уменьшается сопротивление разветвлений, так что давление полностью не теряется. Более того, поскольку [латекс] Q = A \ overline {v} \\ [/ latex] и A увеличивается за счет ветвления, средняя скорость кровотока в меньших сосудах снижается. Скорость крови в аорте (диаметр = 1 см) составляет около 25 см / с, в то время как в капиллярах (диаметром 20 мкм м) скорость составляет около 1 мм / с.Эта пониженная скорость позволяет крови обмениваться веществами с клетками капилляров и, в частности, альвеол.
Сводка раздела
- Ламинарный поток характеризуется плавным течением жидкости слоями, которые не смешиваются.
- Турбулентность характеризуется вихрями и завихрениями, которые смешивают слои жидкости вместе.
- Вязкость жидкости [латекс] \ эта [/ латекс] обусловлена трением внутри жидкости. Типичные значения приведены в таблице 1.{4}} {8 \ eta l} \\ [/ латекс].
- Падение давления, вызванное потоком и сопротивлением, определяется по формуле
[латекс] {P} _ {2} — {P} _ {1} = RQ [/ латекс].
Концептуальные вопросы
1. Объясните, почему вязкость жидкости уменьшается с температурой, то есть как повышение температуры может уменьшить влияние сил сцепления в жидкости? Также объясните, почему вязкость газа увеличивается с температурой, то есть как повышение температуры газа приводит к большему количеству столкновений между атомами и молекулами?
2.При гребле на каноэ вверх по течению разумнее всего плыть как можно ближе к берегу. Во время плавания на каноэ вниз по течению лучше держаться посередине. Объяснить, почему.
3. Почему в душе уменьшается поток, когда кто-то смывает воду из унитаза?
4. Сантехника обычно включает заполненные воздухом трубы возле водопроводных кранов, как показано на рисунке 8. Объясните, зачем они нужны и как они работают.
Рис. 8. Вертикальная трубка рядом с водопроводным краном остается наполненной воздухом и служит полезной цели.
Задачи и упражнения
1. (a) Рассчитайте тормозящую силу, обусловленную вязкостью слоя воздуха между тележкой и ровной воздушной дорожкой, учитывая следующую информацию: температура воздуха 20º C, тележка движется со скоростью 0,400 м / с, площадь ее поверхности составляет 2,50 × 10 -2 м 2 , а толщина воздушного слоя составляет 6,00 × 10 -5 м. б) Каково отношение этой силы к весу тележки весом 0,300 кг?
2. Какое усилие необходимо, чтобы натянуть одно предметное стекло микроскопа на другое со скоростью 1?00 см / с, если между ними находится слой воды толщиной 20,0º толщиной 0,500 мм и площадь контакта 8,00 см 2 ?
Какое усилие необходимо, чтобы натянуть одно предметное стекло микроскопа на другое со скоростью 1?00 см / с, если между ними находится слой воды толщиной 20,0º толщиной 0,500 мм и площадь контакта 8,00 см 2 ?
3. Раствор глюкозы, вводимый внутривенно, имеет скорость потока 4,00 см 3 / мин. Какой будет новый расход, если глюкозу заменить цельной кровью, имеющей такую же плотность, но вязкость в 2,50 раза больше, чем у глюкозы? Все остальные факторы остаются неизменными.
4. Перепад давления по длине артерии 100 Па, радиус 10 мм, поток ламинарный.Средняя скорость кровотока 15 мм / с. а) Какова суммарная сила, действующая на кровь в этом участке артерии? б) Какая сила расходуется на поддержание потока?
5. Маленькая артерия имеет длину 1,1 × 10 -3 и радиус 2,5 × 10 -5 . Если перепад давления в артерии составляет 1,3 кПа, какова скорость потока через артерию? (Предположим, что температура 37ºC.)
6. Изначально жидкость течет по трубке со скоростью 100 см 3 / с.Чтобы проиллюстрировать чувствительность расхода к различным факторам, рассчитайте новый расход для следующих изменений, оставив все остальные факторы такими же, как в исходных условиях. (a) Перепад давления увеличивается в 1,50 раза. (b) Заменяется новая жидкость с вязкостью в 3,00 раза большей. (c) Трубку заменяют на трубку, длина которой в 4 раза больше. (d) Используется другая трубка с радиусом в 0,100 раза больше исходного. (e) заменяется еще одна трубка с радиусом в 0,100 раза больше исходного и половиной длины, и , перепад давления увеличивается в 1 раз.50.
7. Артериолы (маленькие артерии), ведущие к органу, сужаются, чтобы уменьшить приток к органу. Чтобы выключить орган, кровоток естественным образом снижается до 1,00% от исходного значения. Насколько уменьшились радиусы артериол? Пингвины делают это, когда стоят на льду, чтобы уменьшить кровоток к ногам.
8. Ангиопластика — это метод, при котором артерии, частично заблокированные бляшками, расширяются для увеличения кровотока. В какой степени необходимо увеличить радиус артерии, чтобы увеличить кровоток в 10 раз?
Ангиопластика — это метод, при котором артерии, частично заблокированные бляшками, расширяются для увеличения кровотока. В какой степени необходимо увеличить радиус артерии, чтобы увеличить кровоток в 10 раз?
9.(a) Предположим, что радиус кровеносного сосуда уменьшился до 90,0% от его первоначального значения из-за отложений зубного налета, и организм компенсирует это увеличением разницы давлений вдоль сосуда, чтобы поддерживать постоянную скорость потока. Во сколько раз должен увеличиваться перепад давления? (b) Если препятствие создает турбулентность, какой дополнительный эффект это может оказать на скорость потока?
10. Сферическая частица, падающая с конечной скоростью в жидкости, должна иметь гравитационную силу, уравновешенную силой сопротивления и выталкивающей силой.{2} g} {9 \ eta} \ left ({\ rho} _ {\ text {s}} — {\ rho} _ {1} \ right) \\ [/ latex],
, где R — радиус сферы, ρ s — ее плотность, ρ 1 — плотность жидкости и η коэффициент вязкости.
11. Используя уравнение предыдущей задачи, найдите вязкость моторного масла, в которое стальной шарик радиусом 0,8 мм падает с конечной скоростью 4,32 см / с. Плотность шара и масла 7.{\ text {2}} \\ [/ latex] и установив это значение равным весу человека, найдите предельную скорость для человека, падающего «распростертым орлом». Найдите формулу и число для v t с предположениями относительно размера.
13. Между двумя предметными стеклами микроскопа помещен слой масла толщиной 1,50 мм. Исследователи обнаружили, что сила 5,50 × 10 -4 Н требуется для скольжения друг над другом со скоростью 1,00 см / с, когда их контактная площадь составляет 6,00 см 2 . Какая вязкость масла? Что это за масло?
14.(a) Убедитесь, что уменьшение ламинарного потока через трубу на 19,0% вызвано уменьшением радиуса на 5,00%, при условии, что все другие факторы остаются постоянными, как указано в тексте. (b) Какое увеличение потока получается при увеличении радиуса на 5,00%, опять же при условии, что все другие факторы остаются постоянными?
(b) Какое увеличение потока получается при увеличении радиуса на 5,00%, опять же при условии, что все другие факторы остаются постоянными?
15. Пример 1 выше относится к потоку физиологического раствора в системе IV. (a) Убедитесь, что давление 1,62 × 10 4 Н / м 2 создается на глубине 1,61 м в солевом растворе, предполагая, что его плотность соответствует плотности морской воды.(b) Рассчитайте новый расход, если высота солевого раствора уменьшится до 1,50 м. (c) На какой высоте направление потока изменится на противоположное? (Этот поворот может стать проблемой, когда пациенты встают.)
16. Когда врачи диагностируют артериальную закупорку, они указывают снижение скорости потока. Если скорость потока в артерии была снижена до 10,0% от своего нормального значения из-за сгустка крови, а средняя разница давления увеличилась на 20,0%, в какой степени сгусток уменьшил радиус артерии?
17.Во время марафонского забега кровоток бегуна увеличивается в 10 раз от ее частоты отдыха. Вязкость ее крови упала до 95,0% от нормального значения, а разница артериального давления в кровеносной системе увеличилась на 50,0%. Во сколько раз увеличился средний радиус ее кровеносных сосудов?
18. Вода, подаваемая в дом по водопроводу, имеет давление 3,00 × 10 5 в начале летнего дня, когда потребление по соседству мало. Это давление создает поток 20.0 л / мин через садовый шланг. Позже днем давление на выходе из водопровода и входе в дом падает, и через тот же шланг получается расход всего 8,00 л / мин. а) Какое давление сейчас подается в дом, если сопротивление постоянное? (b) На какой фактор увеличился расход в водопроводной магистрали, чтобы вызвать это снижение подаваемого давления? Давление на входе в водопровод составляет 5,00 × 10 5 Н / м, а исходный расход составлял 200 л / мин.(c) Сколько еще пользователей, если предположить, что каждый будет потреблять 20,0 л / мин утром?
19. Нефтяной фонтан выбрасывает сырую нефть на 25,0 м в воздух по трубе диаметром 0,100 м. Пренебрегая сопротивлением воздуха, но не сопротивлением трубы, и предполагая ламинарный поток, рассчитайте манометрическое давление на входе в вертикальную трубу длиной 50,0 м. Примем плотность масла 900 кг / м 3 и вязкость 1,00 (Н / м 2 ) с (или 1,00 Па с).Учтите, что необходимо учитывать давление из-за 50-метрового столба масла в трубе.
Нефтяной фонтан выбрасывает сырую нефть на 25,0 м в воздух по трубе диаметром 0,100 м. Пренебрегая сопротивлением воздуха, но не сопротивлением трубы, и предполагая ламинарный поток, рассчитайте манометрическое давление на входе в вертикальную трубу длиной 50,0 м. Примем плотность масла 900 кг / м 3 и вязкость 1,00 (Н / м 2 ) с (или 1,00 Па с).Учтите, что необходимо учитывать давление из-за 50-метрового столба масла в трубе.
20. Бетон перекачивается из бетономешалки к месту укладки, а не в тачках. Скорость потока составляет 200,0 л / мин через шланг длиной 50,0 м и диаметром 8,00 см, а давление в насосе составляет 8,00 × 10 6 Н / м 2 . (а) Рассчитайте сопротивление шланга. б) Какова вязкость бетона, если предположить, что поток ламинарный? (c) Какая мощность подается, если предположить, что точка использования находится на том же уровне, что и насос? Вы можете пренебречь мощностью, подаваемой для увеличения скорости бетона.
21. Создай свою проблему Рассмотрим коронарную артерию, суженную артериосклерозом. Постройте задачу, в которой вы вычисляете величину уменьшения диаметра артерии на основе оценки уменьшения скорости потока.
22. Представьте себе реку, которая протекает в районе дельты на пути к морю. Постройте задачу, в которой вы вычисляете среднюю скорость, с которой вода движется в районе дельты, на основе скорости, с которой она движется вверх по реке.Среди вещей, которые следует учитывать, — размер и скорость течения реки до того, как она расширится, и ее размер после того, как она расширится. Вы можете построить задачу для реки, которая переходит в одну большую реку или на несколько меньших рек.
Глоссарий
- ламинарный:
- Тип потока жидкости, в котором слои не смешиваются
- турбулентность:
- Поток жидкости, в котором слои смешиваются вместе посредством завихрений и завихрений
- вязкость:
- трение в жидкости, определяемое как трение между слоями
- Закон Пуазейля для сопротивления:
- сопротивление ламинарному течению несжимаемой жидкости в трубке: R = 8 ηl / πr 4
- Закон Пуазейля:
- скорость ламинарного течения несжимаемой жидкости в трубке: Q = ( P 2 — P 1 ) πr 4 /8 ηl
Избранные решения проблем и упражнения
1. (а) 3.02 × 10 -3 N (б) 1.03 × 10 -3
(а) 3.02 × 10 -3 N (б) 1.03 × 10 -3
3. 1.60 см 3 / мин
5. 8,7 × 1o -11 м 3 / с
7. 0,316
9. (a) 1,52 (b) Турбулентность снизит скорость кровотока, что потребует еще большего увеличения разницы давлений, что приведет к повышению артериального давления.
11,225 мПа с
13. 0,138 Па с или оливковое масло.
15. (а) 1,62 × 10 4 Н / м 2 (б) 0.111 см 3 / с (в) 10,6 см
17. 1,59
19. 2,95 × 10 6 Н / м 2 (избыточное давление)
ПОСОБИЕ ДАВЛЕНИЯ В ТРУБОПРОВОДНЫХ СИСТЕМАХ
Скачок давления в системе трубопроводов, известный как гидравлический или гидравлический удар, происходит всякий раз, когда линейный расход жидкости в трубе быстро изменяется — при запуске или остановке насосов клапаны открываются или закрываются с быстрым действующих исполнительных устройств, или захваченный воздух перемещается внутри системы.Чем длиннее трубопровод и чем быстрее движется жидкость, тем выше вероятность удара.
Скачки давления создают нагрузку на материалы и соединения трубопроводов и могут вызвать физическое перемещение трубопроводной системы. Инженерные проекты должны включать средства управления, которые могут поддерживать скачки давления в пределах возможностей системы трубопроводов и устранять или минимизировать физическое движение системы. Вполне возможно, что импульсное давление будет вдвое выше нормального рабочего давления. На долговременную работу системы трубопроводов могут повлиять повторяющиеся ударные волны, что может привести к утечкам и другим дорогостоящим повреждениям.
Некоторые проблемы с импульсным давлением возникают из-за плохой конструкции системы трубопроводов — независимо от того, какой материал используется для системы. Например, слишком быстрое уменьшение размера трубы может привести к проблемам с импульсным давлением. Система может включать 8-дюймовую трубу при входе в тройник и сокращать до двух 3-дюймовых труб, выходящих из тройника. В такой ситуации внутри тройника создается скачок давления, поскольку линейная скорость жидкости должна значительно увеличиваться, чтобы протолкнуть тот же объемный расход через меньшее поперечное сечение потока.
Система может включать 8-дюймовую трубу при входе в тройник и сокращать до двух 3-дюймовых труб, выходящих из тройника. В такой ситуации внутри тройника создается скачок давления, поскольку линейная скорость жидкости должна значительно увеличиваться, чтобы протолкнуть тот же объемный расход через меньшее поперечное сечение потока.
Различные материалы по-разному действуют в условиях импульсного давления в зависимости от их прочности и эластичности. Понимание материала, используемого в системе трубопроводов, и разработка системы для регулирования давления и скорости потока жидкости в соответствии с ее возможностями важны для долгосрочной работы системы. Правильный выбор размера трубы по всей системе, регулирование скорости, с которой срабатывают клапаны и насосы, а также включение устройств для демпфирования гидроудара могут ограничить воздействие гидравлического удара и сохранить общее давление в системе в пределах проектных параметров.
Расчет импульсного давленияКонструкторы и инженеры могут управлять некоторыми факторами, относящимися к импульсному давлению, такими как диаметр трубы и скорость жидкости, в то время как такие факторы, как свойства жидкости, зависят от области применения. Инженеры могут использовать следующее уравнение для расчета максимального импульсного давления в трубопроводной системе:
Пульсирующее давление всегда следует рассчитывать как добавку к рабочему давлению в системе.Комбинированное импульсное давление и рабочее давление никогда не должны превышать в 1,5 раза максимальное рабочее давление системы.
Значения в таблицах, связанных ниже, основаны на приведенной выше формуле при 73 ° F и предположении, что вода, текущая с заданной скоростью галлонов в минуту, внезапно и полностью прекратится. Пульсирующее давление примерно на 15 процентов меньше при 180 ° F. Значения для жидкостей, отличных от воды, могут быть рассчитаны путем умножения квадратного корня из удельного веса жидкости.
В следующих таблицах показана несущая способность и потери на трение для трубопроводов по Графику 80 и включены как независимые, так и зависимые переменные.
Пропускная способность и потери на трение для трубы Corzan CPVC Schedule 80 (PDF)
Конструкция для минимизации скачков давления У инженеровесть несколько вариантов при проектировании систем трубопроводов, которые помогут минимизировать негативное влияние скачков давления. Например, правильный выбор размеров труб — самый эффективный способ контролировать скорость жидкости. Чем больше диаметр трубы, тем меньше скорость жидкости для данного объемного расхода. Эту переменную следует отрегулировать для поддержания требуемого расхода при поддержании давления помпажа ниже 1.В 5 раз превышающее максимальное рабочее давление материала трубопровода.
Линейная скорость потока жидкости в системе трубопроводов обычно должна быть ограничена до 5 футов / с для промышленных применений, особенно для труб диаметром шесть дюймов или больше. Ни в коем случае нельзя допускать скопления воздуха в системе во время ее работы. Во время запуска скорость жидкости в системе должна быть ограничена до 1 фут / с при заполнении или до тех пор, пока весь воздух не будет удален, а давление не будет доведено до рабочих условий. Кроме того, нельзя позволять насосам всасывать воздух.
Можно использовать дополнительные средства защиты для предотвращения скачков давления или гидравлических ударов в трубопроводах. Такое оборудование может включать клапаны сброса давления, амортизаторы, ограничители перенапряжения и клапаны сброса вакуума воздуха. Клапаны быстрого действия всегда следует регулировать, чтобы предотвратить гидравлический удар.
Сочетание качественных трубопроводов и надлежащей конструкции для надежной и долгосрочной работы Чрезмерное импульсное давление создает дополнительную нагрузку на материалы и соединения и может со временем утомить систему до точки отказа. Различные материалы по-разному работают в ситуациях импульсного давления в зависимости от их прочности и эластичности, поэтому важно понимать материал, который будет использоваться для системы трубопроводов, и правильно спроектировать систему, чтобы избежать дорогостоящих проблем с импульсным давлением.
Различные материалы по-разному работают в ситуациях импульсного давления в зависимости от их прочности и эластичности, поэтому важно понимать материал, который будет использоваться для системы трубопроводов, и правильно спроектировать систему, чтобы избежать дорогостоящих проблем с импульсным давлением.
При правильной конструкции и установке система трубопроводов Corzan из CPVC обеспечит годы надежной и продуктивной службы с минимальными затратами в течение жизненного цикла. За более чем 60 лет успешной работы в различных сложных промышленных условиях, Corzan CPVC предлагает превосходный баланс свойств для удовлетворения конкретных потребностей применения.
Узнайте больше о трубопроводах Corzan из CPVC и о том, как минимизировать импульсное давление в промышленных приложениях. Обратитесь к консультанту по трубопроводным системам Corzan или к производителю-партнеру для получения бесплатной консультации.
Подробная информация для этого блога частично взята из следующих ресурсов:
https://www.corzan.com/en-us/piping-systems/specification/fluid-handling
https://www.corzan.com/blog/how-to-optimize-a-piping-system-to-protect-against-surge-pressure-damage
http: // www.corzan.com/hubfs/Corzan%20CPVC%20Engineering%20Design%20Manual.pdf?t=1500573170875
Как жидкость течет в трубах — Accendo Reliability
Жидкость — это жидкость или газ. В промышленности они перекачиваются от хранилища к месту использования. Правильная конструкция и установка системы трубопроводов сводят к минимуму потери давления и улучшают характеристики оборудования и процессов.
В этой статье кратко объясняется, что происходит с жидкостями, протекающими по трубам.
Стенка трубы
Жидкость, протекающая по трубе, контактирует со стенкой трубы. Стенка трубы имеет шероховатость поверхности. Степень шероховатости влияет на сопротивление жидкости. Шероховатость измеряется высотой выступов, выступающих из стенки трубы.
В ложбинах между выступами жидкость движется медленно. Выше проекций он движется быстрее. Сопротивление между слоями разрывает или разрывает их, и каждый слой движется с разной скоростью. Скорость сдвига уменьшается по мере удаления от стены.Скорость у стены равна нулю и самая высокая в центре. Это означает, что центральная сердцевина жидкости выходит из трубы первой.
Рисунок 1: Скорость потока через трение трубыи ламинарный подслой
Из-за трения, вызываемого стенкой трубы, жидкость движется к стенке медленнее. Эта медленно движущаяся жидкость известна как ламинарный подслой. В этом слое жидкость скользит по себе. Толщина подслоя может варьироваться от десятых долей миллиметра до нескольких миллиметров в зависимости от скорости потока, высоты выступов стенок и физических свойств жидкости.Подслой развивается только в турбулентных (быстрых) потоках. При медленных потоках подслой сливается с пластинчатым (медленным) потоком в трубе. На рисунке 1 показано влияние на скорость потока поверхности стенки трубы.
Вдали от стенки трубы поток турбулентный. В этой области есть водовороты и вихри, беспорядочно перемещающиеся по трубе из стороны в сторону и сверху вниз. Это область, где беспорядочные комки жидкости «болтают» по трубе. Между ламинарной и турбулентной областями находится короткая переходная зона, поскольку поток меняется на турбулентный.
Влияние вязкости и плотности
Не все жидкости ведут себя одинаково. Кровь имеет другие характеристики потока, чем вода. Краска течет иначе, чем бензин. Жидкости классифицируются по их поведению при сдвиге. Те жидкости, которые имеют постоянную скорость сдвига с изменением скорости (например, вода), называются ньютоновскими (Ньютон первым разработал математическое объяснение этого явления). Те, у которых скорость сдвига меняется с изменением скорости (например, краска и кровь), являются неньютоновскими.Скорость сдвига является мерой вязкости или скользкости жидкости.
Плотность жидкости влияет на ее вязкость. Жидкости с большей массой на единицу объема тяжелее и требуют больше энергии для их перемещения и менее легкого сдвига. Повышение температуры снижает вязкость и плотность жидкостей.
Жидкости с большей массой на единицу объема тяжелее и требуют больше энергии для их перемещения и менее легкого сдвига. Повышение температуры снижает вязкость и плотность жидкостей.
Чем более вязкая или менее скользкая жидкость, тем труднее добиться сдвига между слоями. Высокая вязкость предотвращает резкие изменения скорости между слоями. Подслой в вязких жидкостях толще, чем в жидкостях с низкой вязкостью.
Эффекты скорости
На низких скоростях весь поток через трубу ламинарный, и жидкость скользит по самой себе. По мере того, как скорость увеличивается, начинают формироваться водовороты, пересекающие слои жидкости. Развивается переход от ламинарного течения к турбулентному. При еще более высоких скоростях поток в сердцевине трубы становится турбулентным с закрученными вихрями повсюду. На рисунке 2 показано, где возникают различные области потока на сопле резервуара.
Рисунок 2 Режимы обтекания на патрубке резервуара.Ламинарный подслой всегда присутствует у стенки трубы.Но по мере того, как скорость увеличивается, энергетические закрученные водовороты начинают воздействовать более глубоко, и подслой начинает истончаться. При еще более высоких скоростях подслой утончается еще больше, и более высокие пики шероховатости остаются в турбулентной области. Если подслой покрывает выступы шероховатостей, стена считается «гладкой». Когда шероховатость стены выходит из подслоя, стена считается «шероховатой». Это означает, что одна и та же стенка может быть как гладкой, так и шероховатой, в зависимости от скорости жидкости.
Эксперименты доказали, что потеря давления в трубе с ламинарным потоком пропорциональна скорости (p ∝ V), тогда как для турбулентного потока потеря давления пропорциональна квадрату скорости (p ∝ V2).Более медленный поток позволяет получить более толстый подслой и создает «гладкую» стенку трубы. Это сводит к минимуму потери по трубе. В турбулентном потоке потеря давления намного больше.
Проектировщик трубопроводной системы должен найти практический баланс между увеличением диаметра трубы для снижения потерь энергии и сохранением небольшого диаметра для снижения затрат на установку.
Незначительные потери в фитингах Piper
Колена, отводы, переходники, тройники и фланцы — все это вызывает отдельные незначительные потери давления.Когда жидкость вынуждена менять направление или обходить разрушение, образуются водовороты. Эти новые закручивающиеся вихри нарушают структуру потока и создают дополнительные потери давления.
Наибольшие потери давления происходят при резких изменениях диаметра и направления. Большая часть потерь приходится на вихревой след ниже по потоку. При проектировании участка трубопровода постепенное изменение схемы потока.
Расход газа
В отличие от жидкости газ сжимаем и его можно сжать.Когда газ сжимается, его плотность увеличивается — по мере сброса давления плотность уменьшается. Газ, поступающий в трубу, начинается при определенном давлении, температуре и соответствующей плотности. Потери на трение по трубе вызывают потерю давления. Если теперь газ находится под более низким давлением, он должен иметь соответственно меньшую плотность. (Он меньше сдавлен, чем был в начале.) Это означает, что плотность текущего газа изменяется по длине трубы. Эффект сильнее при высоких скоростях.
Для того, чтобы масса газа попала в трубу, такая же масса должна покинуть трубу. Мы знаем, что плотность постоянно уменьшается по мере падения давления в трубе. Один килограмм менее плотного газа требует больше места (объема), чем такой же вес более сжатого газа. Чтобы получить один килограмм расширяющегося газа, который занимает больше объема, из конца трубы он должен идти быстрее, чем когда он входил в трубу. Газ, протекающий по трубе, расширяется при падении давления и ускоряется по мере продвижения по трубе.
Расширяющийся газ охлаждается. Этот принцип используется в холодильниках и кондиционерах. Газ, текущий в трубе, расширяется при падении плотности. Вот почему трубопроводы сжатого воздуха холодные на ощупь, а капли воды собираются в приводах пневматических клапанов. Температура упала достаточно низко, чтобы конденсировать водяной пар.
Майк Сондалини — инженер по техническому обслуживанию
Мы (Accendo Reliability) опубликовали эту статью с любезного разрешения Feed Forward Publishing, дочерней компании BIN95.com
Интернет: trade-school.education
Эл. Почта: [email protected]
Если вам это показалось интересным, вам может понравиться электронная книга Process Control Essentials.
Справка по викторине: Поток жидкости | EZ-pdh.com
Используйте поиск, чтобы быстро найти ответы на вопросы — откройте окно поиска (ctrl + f), затем введите ключевое слово из вопроса, чтобы перейти к этим терминам в материале курса
ВведениеПоток жидкости — важная часть большинства промышленных процессов; особенно те, которые связаны с передачей тепла.Часто, когда требуется отвести тепло из точки, в которой оно генерируется, в процессе теплопередачи участвует какой-либо тип жидкости. Примерами этого являются охлаждающая вода, циркулирующая через бензиновый или дизельный двигатель, поток воздуха, проходящий через обмотки двигателя, и поток воды через активную зону ядерного реактора. Системы подачи жидкости также обычно используются для смазки.
Течение жидкости в ядерной области может быть сложным и не всегда подлежит строгому математическому анализу.В отличие от твердых тел, частицы жидкости движутся по трубопроводу и компонентам с разной скоростью и часто подвергаются разным ускорениям.
Несмотря на то, что подробный анализ потока жидкости может быть чрезвычайно трудным, основные концепции, связанные с проблемами потока жидкости, довольно просты. Эти базовые концепции могут быть применены при решении проблем потока жидкости путем использования упрощающих допущений и средних значений, где это необходимо. Несмотря на то, что такого типа анализа было бы недостаточно при инженерном проектировании систем, он очень полезен для понимания работы систем и прогнозирования приблизительной реакции жидкостных систем на изменения рабочих параметров.
Основные принципы потока жидкости включают три концепции или принципа; первые два из которых студент был представлен в предыдущих руководствах. Первый — это принцип количества движения (приводящий к уравнениям сил жидкости), который был рассмотрен в руководстве по классической физике. Второй — это сохранение энергии (ведущее к первому закону термодинамики), которое изучалось в термодинамике. Третий — это сохранение массы (приводящее к уравнению неразрывности), которое будет объяснено в этом модуле.
Свойства жидкостейЖидкость — это любое вещество, которое течет, потому что его частицы не прикреплены жестко друг к другу. Сюда входят жидкости, газы и даже некоторые материалы, которые обычно считаются твердыми телами, например стекло. По сути, жидкости — это материалы, которые не имеют повторяющейся кристаллической структуры.
Некоторые свойства жидкостей обсуждались в разделе «Термодинамика» этого текста. К ним относятся температура, давление, масса, удельный объем и плотность. Температура была определена как относительная мера того, насколько горячий или холодный материал. Его можно использовать для прогнозирования направления передачи тепла. Давление определялось как сила на единицу площади. Обычными единицами измерения давления являются фунты силы на квадратный дюйм (psi). Масса определяется как количество вещества, содержащегося в теле, и его следует отличать от веса, который измеряется силой тяжести на теле. Удельный объем вещества — это объем на единицу массы вещества.Типичные единицы: футы 3 / фунт. Плотность — это масса вещества на единицу объема. Типичные единицы — фунт / фут 3 . Плотность и удельный объем противоположны друг другу. И плотность, и удельный объем зависят от температуры и в некоторой степени от давления жидкости. По мере увеличения температуры жидкости плотность уменьшается, а удельный объем увеличивается. Поскольку жидкости считаются несжимаемыми, увеличение давления не приведет к изменению плотности или удельного объема жидкости.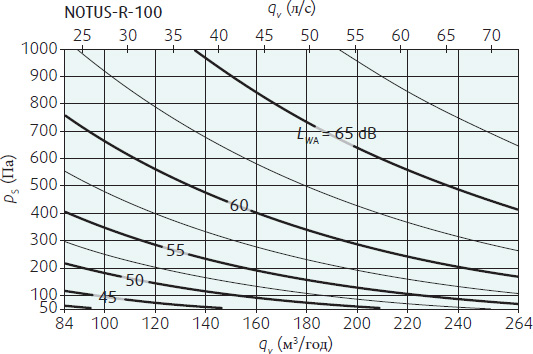 На самом деле жидкости можно слегка сжимать при высоких давлениях, что приводит к небольшому увеличению плотности и небольшому уменьшению удельного объема жидкости.
На самом деле жидкости можно слегка сжимать при высоких давлениях, что приводит к небольшому увеличению плотности и небольшому уменьшению удельного объема жидкости.
Плавучесть определяется как тенденция тела плавать или подниматься при погружении в жидкость. У всех нас было множество возможностей наблюдать плавучие эффекты жидкости. Когда мы идем плавать, наши тела почти полностью поддерживаются водой. Дерево, лед и пробка плавают на воде.Когда мы поднимаем камень с русла ручья, он внезапно кажется тяжелее, выходя из воды. Лодки полагаются на эту плавучую силу, чтобы оставаться на плаву. Величина этого плавучего эффекта была впервые вычислена и указана греческим философом Архимедом. Когда тело помещается в жидкость, оно поддерживается силой, равной весу вытесняемой им воды.
Если тело весит больше, чем жидкость, которую оно вытесняет, оно тонет, но будет казаться, что теряет вес, равный весу вытесненной жидкости, как наша скала.Если тело весит меньше, чем вес вытесненной жидкости, тело поднимется на поверхность, в конце концов, плавая на такой глубине, которая вытеснит объем жидкости, вес которой будет равен его собственному весу. Плавающее тело вытесняет текучую среду, в которой оно плавает, под собственным весом.
СжимаемостьСжимаемость — это мера изменения объема, которому подвергается вещество, когда на вещество оказывается давление. Жидкости обычно считаются несжимаемыми.Например, давление 16 400 фунтов на квадратный дюйм приведет к уменьшению данного объема воды всего на 5% от его объема при атмосферном давлении. С другой стороны, газы очень сжимаются. Объем газа можно легко изменить, оказав на газ внешнее давление.
Взаимосвязь между глубиной и давлением Любой, кто ныряет под поверхность воды, замечает, что давление на его барабанные перепонки даже на глубине несколько футов заметно больше атмосферного давления.Тщательные измерения показывают, что давление жидкости прямо пропорционально глубине, и для данной глубины жидкость оказывает одинаковое давление во всех направлениях.
Как показано на Рисунке 1, давление на разных уровнях в резервуаре меняется, и это заставляет жидкость покидать резервуар с разными скоростями. Давление определялось как сила на единицу площади. В случае этого резервуара сила возникает из-за веса воды выше точки, в которой определяется давление.
Давление = Сила / Площадь
= Вес / Площадь
P = (мг) / (A g c )
= (ρ V g) / (A g c )
Где:
m = масса в фунтах / м
g = ускорение свободного падения 32,17 фут / сек 2
g c = 32 фунт-фут / фунт-сила-сек 2
A = площадь в футах 2
V = объем в футах 3
ρ = плотность жидкости в фунтах / фут 3
Объем равен площади поперечного сечения, умноженной на высоту (h) жидкости.Подставляя это в приведенное выше уравнение, получаем:
P = (ρ A hg) / (A g c )
P = (ρ hg) / (g c )
Это уравнение говорит нам, что давление оказываемое водяным столбом прямо пропорционально высоте столба и плотности воды и не зависит от площади поперечного сечения столба. Давление на тридцать футов ниже поверхности стояка диаметром один дюйм такое же, как давление на тридцать футов ниже поверхности большого озера.
Пример 1:Если резервуар на Рисунке 1 заполнен водой с плотностью 62,4 фунта / фут3, рассчитайте давление на глубинах 10, 20 и 30 футов.
Решение:
P = (ρhg) / g c
P 10 футов = (62,4 фунт / фут 3 ) (1o ft) (32,17 фут / с 2 / (32,17 фунт-м- фут / фунт-сила / дюйм 2 )
= 624 фунт-сила / фут 2 (1 фут 2 /144 дюйм 2 )
= 4,33 фунт-силы / дюйм 2
P 20 = ( 624 фунт / фут 3 ) (20 футов) (32.17 футов / с 2 / (32,17 фунт-фут / фунт-сила-с 2 )
= 1248 фунт-сила / фут 2 (1 фут 2 /144 дюйма 2 )
= 8,67 фунт-фут / дюйм
P 30 футов = (62,4 фунта / фут3) (30 футов) (32,17 фут / сек 2 / 32,17 фунт-фут / фунт-сила-сек 2 )
= 1872 фунт-сила / фут 2 (1 футов 2 /144 дюймов 2 )
= 13,00 фунт-сил / дюйм 2
Пример 2: Цилиндрический резервуар для воды высотой 40 футов и диаметром 20 футов заполнен водой с плотностью из 61.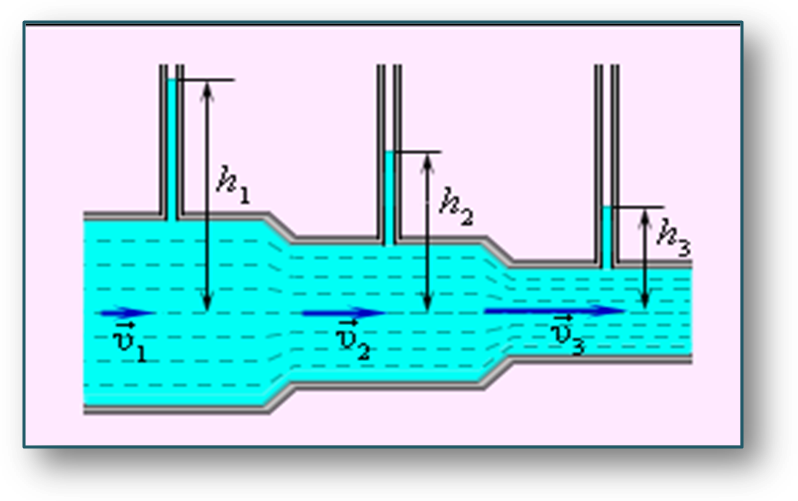 9 фунт / фут 3 .
9 фунт / фут 3 .
(а) Какое давление воды на дне резервуара?
(b) Какая средняя сила действует на дно?
Решение:
(a) P = (phg) / g c
P = (61,9 фунт / фут 3 ) (40 футов) (32,17 фут / сек 2 / 32,17 фунт-фут / фут) фунт-сила-сек 2 )
= 2476 фунт-сила / фут 2 (1 фут 2 /144 дюйм 2 )
= 17,2 фунт-сила / дюйм 2
(b) Давление = сила / площадь
Сила = (Давление) (Площадь)
Площадь = πr 2
F = (17.2 фунта-силы / дюйм 2 ) π (10 футов) 2 (144 дюйма 2 /1 фут 2 )
= 7,78 x 10 5 фунт-сила
Закон Паскаля
Давление жидкостей в каждом из ранее упомянутых случаев было связано с весом жидкости. Давление жидкости также может быть результатом приложения внешних сил к жидкости. Рассмотрим следующие примеры. На рисунке 2 изображен контейнер, полностью заполненный жидкостью. A, B, C, D и E представляют собой поршни одинаковой площади поперечного сечения, вставленные в стенки резервуара.На поршни C, D и E будут действовать силы из-за давления, вызванного разной глубиной жидкости. Предположим, что силы, действующие на поршни из-за давления, вызванного весом жидкости, следующие: A = 0 фунтов-силы, B = 0 фунтов-силы, C = 10 фунтов-силы, D = 30 фунтов-силы и E = 25 фунтов-силы. Теперь позвольте приложить к поршню А внешнюю силу в 50 фунтов-силы. Эта внешняя сила вызовет повышение давления во всех точках контейнера на такую же величину. Поскольку все поршни имеют одинаковую площадь поперечного сечения, увеличение давления приведет к тому, что силы, действующие на поршни, увеличатся на 50 фунтов-силы.Таким образом, если к поршню A приложена внешняя сила в 50 фунтов-силы, сила, оказываемая жидкостью на другие поршни, теперь будет следующей: B = 50 фунтов-силы, C = 60 фунтов-силы, D = 80 фунтов-силы и E = 75 фунтов-силы. . »
. »
Этот эффект внешней силы на замкнутый флюид был впервые заявлен Паскалем в 1653 году.
Давление, приложенное к замкнутому флюиду, передается в неизменном виде по замкнутому сосуду системы
.
Контрольный объем
В термодинамике контрольный объем был определен как фиксированная область в пространстве, где изучаются массы и энергии, пересекающие границы области.Эта концепция контрольного объема также очень полезна при анализе проблем потока жидкости. Граница контрольного объема для потока жидкости обычно принимается за физическую границу части, через которую протекает поток. Концепция контрольного объема используется в приложениях гидродинамики с использованием принципов непрерывности, импульса и энергии, упомянутых в начале этой главы. После того, как контрольный объем и его граница установлены, различные формы энергии, пересекающие границу с жидкостью, могут быть рассмотрены в форме уравнения для решения проблемы жидкости.Поскольку в задачах потока жидкости обычно рассматривается жидкость, пересекающая границы контрольного объема, подход контрольного объема упоминается как «открытый» системный анализ, аналогичный концепциям, изучаемым в термодинамике. В ядерной области есть особые случаи, когда жидкость не пересекает контрольную границу. Подобные случаи изучаются с использованием «закрытого» системного подхода.
Независимо от природы потока, все ситуации, связанные с потоком, подчиняются установленным основным законам природы, которые инженеры выразили в форме уравнений.Сохранение массы и сохранение энергии всегда выполняются в задачах с жидкостью, наряду с законами движения Ньютона. Кроме того, каждая задача будет иметь физические ограничения, называемые математически граничными условиями, которые должны быть выполнены, прежде чем решение проблемы будет согласовано с физическими результатами.
Объемный расход Объемный расход расход расход (V˙) системы — это мера объема жидкости, проходящей через точку в системе за единицу времени. Объемный расход можно рассчитать как произведение площади поперечного сечения (A) потока и средней скорости потока (v).
Объемный расход можно рассчитать как произведение площади поперечного сечения (A) потока и средней скорости потока (v).
V˙ = A v (3-1)
Если площадь измеряется в квадратных футах, а скорость — в футах в секунду, уравнение 3-1 приводит к объемному расходу, измеренному в кубических футах в секунду. Другие распространенные единицы объемного расхода включают галлоны в минуту, кубические сантиметры в секунду, литры в минуту и галлоны в час.
Пример:Труба с внутренним диаметром 4 дюйма содержит воду, которая течет со средней скоростью 14 футов в секунду.Рассчитайте объемный расход воды в трубе.
Решение:
Используйте уравнение 3-1 и замените площадь.
V˙ = (π r 2) v
V˙ = (3,14) (2/12 фута) 2 (14 футов / сек)
V˙ = 1,22 фута 3 / сек
Масса РасходМассовый расход (м²) системы — это мера массы жидкости, проходящей через точку в системе за единицу времени. Массовый расход связан с объемным расходом, как показано в уравнении 3-2, где ρ — плотность жидкости.
м˙ = ρV˙ (3-2)
Если объемный расход выражен в кубических футах в секунду, а плотность выражена в фунтах массы на кубический фут, уравнение 3-2 приводит к массовому расходу, измеренному в фунтах: масса в секунду. Другие распространенные единицы измерения массового расхода включают килограммы в секунду и фунты массы в час.
Замена V˙ в уравнении 3-2 соответствующими членами из уравнения 3-1 позволяет напрямую рассчитать массовый расход.
м˙ = ρ A v (3-3)
Пример:Вода в трубе из предыдущего примера имела плотность 62.44 фунт / фут3. Рассчитайте массовый расход.
Решение:
м˙ = ρ V˙
м˙ = (62,44 фунта / фут 3 ) (1,22 фута 3 / сек)
м˙ = 76,2 фунта / сек
Сохранение массы В термодинамике вы узнали, что энергия не может быть ни создана, ни уничтожена, а только изменена по форме. То же самое и с массой. Сохранение массы — это инженерный принцип, который гласит, что все массовые расходы в контрольном объеме равны всем массовым расходам из контрольного объема плюс скорость изменения массы в контрольном объеме.Математически этот принцип выражается уравнением 3-4.
То же самое и с массой. Сохранение массы — это инженерный принцип, который гласит, что все массовые расходы в контрольном объеме равны всем массовым расходам из контрольного объема плюс скорость изменения массы в контрольном объеме.Математически этот принцип выражается уравнением 3-4.
м˙
дюйм = м˙ выход + ∆m / ∆t (3-4)где:
∆m / ∆t = увеличение или уменьшение массы в пределах контрольного объема за ( указанный период времени)
Устойчивый потокУстойчивый поток относится к состоянию, при котором свойства жидкости в любой отдельной точке системы не меняются с течением времени. Эти свойства жидкости включают температуру, давление и скорость.Одним из наиболее важных свойств, которое является постоянным в системе с установившимся потоком, является массовый расход системы. Это означает, что в каком-либо компоненте системы не происходит накопления массы.
Уравнение неразрывностиУравнение неразрывности — это просто математическое выражение принципа сохранения массы. Для контрольного объема с одним входом и одним выходом принцип сохранения массы гласит, что для установившегося потока массовый расход в объеме должен равняться массовому расходу на выходе.Уравнение неразрывности для этой ситуации выражается уравнением 3-5.
м˙
вход = м˙ выход (3-5)(ρAv) вход = (ρAv) выход
Для контрольного объема с несколькими входами и выходами принцип сохранения масса требует, чтобы сумма массовых расходов в контрольном объеме была равна сумме массовых расходов из контрольного объема. Уравнение неразрывности для этой более общей ситуации выражается уравнением 3-6.
∑ м˙
входов = м˙ выходов (3-6) Одним из простейших приложений уравнения неразрывности является определение изменения скорости жидкости
из-за расширения или сжатия диаметра трубка.
Установившийся поток существует в трубе, которая постепенно расширяется с диаметра 6 дюймов до диаметра 8 дюймов. Плотность жидкости в трубе постоянна и равна 60 .8 фунт / фут3. Если скорость потока составляет 22,4 фута / сек в секции 6 дюймов, какова скорость потока в секции 8 дюймов?
Плотность жидкости в трубе постоянна и равна 60 .8 фунт / фут3. Если скорость потока составляет 22,4 фута / сек в секции 6 дюймов, какова скорость потока в секции 8 дюймов?
Решение:
Из уравнения неразрывности мы знаем, что массовый расход в секции 6 дюймов должен равняться массовому расходу в секции 8 дюймов. Пусть нижний индекс 1 представляет 6-дюймовую секцию, а 2 — 8-дюймовую секцию, мы получаем следующее.
m˙ 1 = m˙ 2
ρ 1 A 1 v 1 = ρ 2 A 2 v 2
v 904 2 = v (ρ 1/ ρ 2 ) (A 1 / A 2 )
v 2 = v 1 (π / r 1 2 ) (π / r 2 2 )
v 2 = (22.4 фута / сек) [(3 дюйма) 2 / (4 дюйма) 2 ]
v 2 = 12,6 фута / сек
Таким образом, используя уравнение неразрывности, мы увеличиваем диаметр трубы от От 6 до 8 дюймов скорость потока снизилась с 22,4 до 12,6 футов / сек.
Уравнение неразрывности также может использоваться, чтобы показать, что уменьшение диаметра трубы приведет к увеличению скорости потока.
Пример: уравнение непрерывности — центробежный насос Рисунок 3: Уравнение непрерывностиВходной диаметр насоса охлаждающей жидкости реактора, показанный на рисунке 3, составляет 28 дюймов.в то время как поток на выходе через насос составляет 9200 фунтов / м3. Плотность воды составляет 49 фунтов на кубический метр. Какая скорость на входе в насос?
Решение:
Вход = πr 2 = (3,13) (14 дюймов ((1 фут / 12 дюймов)) 2
= 4,28 фута 2
м˙ вход = м ˙ на выходе = 9200 фунтов / с
(ρAv) на входе = 9200 фунтов / с
на входе = 9200 фунтов / с / Aρ
= (9200 фунтов / с) / [(4. 28 футов 2) (49 фунтов / фут 3 )]
28 футов 2) (49 фунтов / фут 3 )]
v на входе = 43,9 футов / сек
Приведенный выше пример показывает, что скорость потока в систему такая же, как и вне системы. Та же самая концепция верна, даже если более одного пути потока могут входить или выходить из системы одновременно. Баланс массы просто регулируется, чтобы указать, что сумма всех потоков, входящих в систему, равна сумме всех потоков, покидающих систему, если существуют установившиеся условия. Пример этого физического случая включен в следующий пример.
Пример: уравнение непрерывности — несколько выходов Рисунок 4: Y-образная конфигурация для примера задачиТрубопроводная система имеет Y-образную конфигурацию для разделения потока, как показано на рисунке 4. Диаметр входной ветви составляет 12 дюймов, а диаметры выпускных колен составляют 8 и 10 дюймов. Скорость в 10-дюймовых опорах составляет 10 футов / сек. Поток через основную часть составляет 500 фунтов / м3. Плотность воды 62,4 фунта / фут3. Какова скорость на участке трубы диаметром 8 дюймов?
Решение:
A 8 = π [4 дюйм.(1 фут / 12 дюймов)] 2
= 0,349 фута 2
A 10 = π [5 дюймов (1 фут / 12 дюймов)] 2
= 0,545 фута 2
Σm˙ входов = Σm˙ выходов
м˙ 12 = m˙ 10 + m˙ 8
м˙ 8 = m˙ 12 10 — m˙
(ρAv) 8 = м˙ 12 — (ρAv) 10
v 8 = (m˙ 12 — (ρAv) 10 ) / (ρA) 8
= [(500 фунт / сек) — (62.4 фунта / фут3) (0,545 фут2) (10 фут / сек)] / (62,4 фунта / фут3) (0,349 фут 2 )
v 8 = 7,3 фут / сек
Основные положения данной главы кратко изложены на следующей странице.
- Изменения плотности жидкости обратно пропорциональны изменениям температуры.

- Плавучесть — это тенденция тела плавать или подниматься при погружении в жидкость.
- Давление , оказываемое водяным столбом, прямо пропорционально высоте столба и плотности воды.
P = ρ h г / г c
- Закон Паскаля гласит, что давление, приложенное к замкнутой жидкости, передается в неизменном виде по замкнутому сосуду системы.
- Объемный расход — это объем жидкости в единицу времени, проходящий через точку в жидкостной системе.
- Массовый расход — это масса жидкости в единицу времени, проходящая через точку в жидкостной системе.
- Объемный расход рассчитывается как произведение средней скорости жидкости и площади поперечного сечения потока.
V˙ = A v
- Массовый расход рассчитывается как произведение объемного расхода и плотности жидкости.
m˙ = ρ A v
- Принцип сохранения массы гласит, что все массовые расходы в контрольном объеме равны всем массовым расходам из контрольного объема плюс скорость изменения масса в контрольном объеме.
- Для контрольного объема с одним входом и выходом уравнение неразрывности может быть выражено следующим образом:
м˙ на входе = м˙ на выходе
- Для контрольного объема с несколькими входами и выходов уравнение непрерывности:
m входов = m выходов
Режимы потока
Весь поток жидкости подразделяется на одну из двух широких категорий или режимов.Эти два режима потока — ламинарный поток и турбулентный поток. Режим потока, будь то ламинарный или турбулентный, важен при проектировании и работе любой жидкостной системы.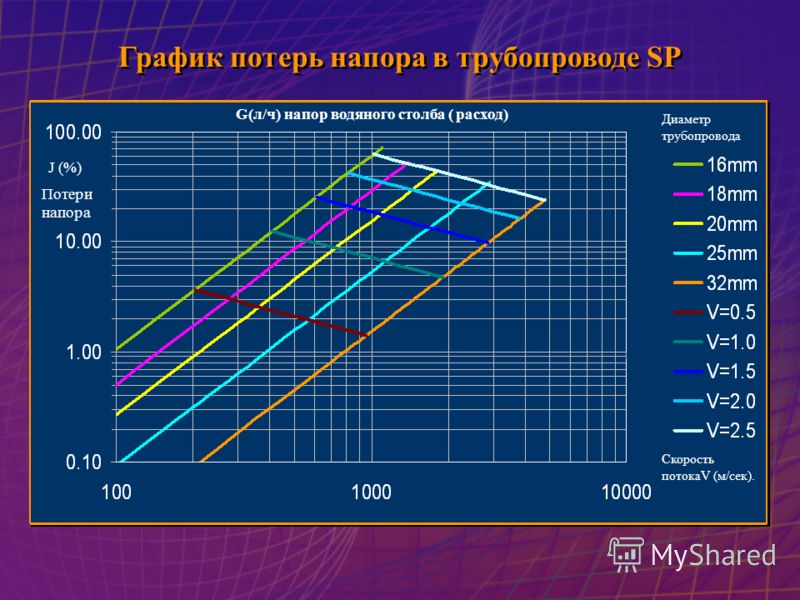 Величина гидравлического трения, которая определяет количество энергии, необходимое для поддержания желаемого потока, зависит от режима потока. Это также является важным соображением в некоторых приложениях, связанных с теплопередачей жидкости.
Величина гидравлического трения, которая определяет количество энергии, необходимое для поддержания желаемого потока, зависит от режима потока. Это также является важным соображением в некоторых приложениях, связанных с теплопередачей жидкости.
Ламинарный поток
Ламинарный поток также называют обтекаемым или вязким потоком.Эти термины описывают поток, потому что в ламинарном потоке (1) слои воды текут друг над другом с разными скоростями практически без перемешивания между слоями, (2) частицы жидкости движутся по определенным и наблюдаемым траекториям или линиям тока и (3) ) течение характерно для вязкой (густой) жидкости или является тем потоком, в котором вязкость жидкости играет значительную роль.
Турбулентный поток
Турбулентный поток характеризуется неравномерным движением частиц жидкости. Нет определенной частоты, как в волновом движении.Частицы движутся по неправильным путям, без видимого рисунка и определенных слоев.
Профили скорости потока
Не все частицы жидкости движутся по трубе с одинаковой скоростью. Форма кривой скорости (профиль скорости на любом заданном участке трубы) зависит от того, является ли поток ламинарным или турбулентным. Если поток в трубе ламинарный, распределение скорости в поперечном сечении будет параболическим по форме с максимальной скоростью в центре, примерно вдвое превышающей среднюю скорость в трубе.В турбулентном потоке существует довольно равномерное распределение скорости по сечению трубы, в результате чего вся жидкость течет с заданным единственным значением. Рисунок 5 помогает проиллюстрировать изложенные выше идеи. Скорость жидкости, контактирующей со стенкой трубы, по существу равна нулю и увеличивается по мере удаления от стенки.
Рисунок 5: Профили скорости ламинарного и турбулентного потока Обратите внимание на рисунок 5, что профиль скорости зависит от состояния поверхности стенки трубы. Более гладкая стенка дает более равномерный профиль скорости, чем грубая стенка трубы.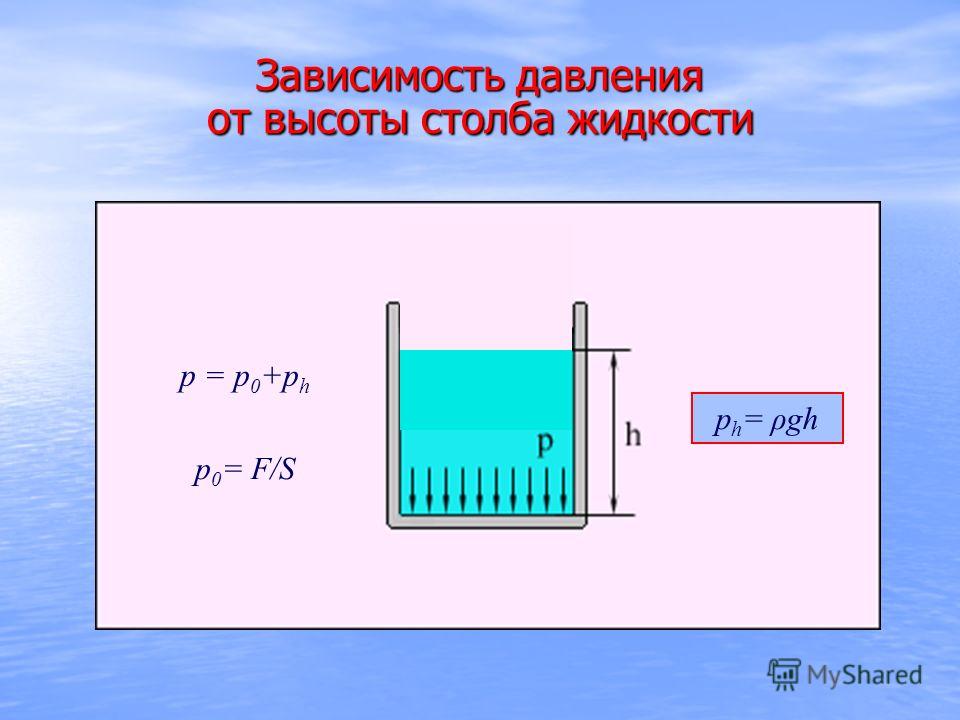
Средняя (объемная) скорость
Во многих задачах потока жидкости вместо определения точных скоростей в разных местах в одном и том же поперечном сечении потока достаточно позволить одной средней скорости представлять скорость всей жидкости в этой точке в трубе. Это довольно просто для турбулентного потока, поскольку профиль скорости плоский по большей части поперечного сечения трубы. Разумно предположить, что средняя скорость равна скорости в центре трубы.
Если режим потока ламинарный (профиль скорости параболический), все еще существует проблема попытки представить «среднюю» скорость в любом заданном поперечном сечении, поскольку среднее значение используется в уравнениях потока жидкости. Технически это делается с помощью интегрального исчисления. На практике ученик должен использовать среднее значение, равное половине значения средней линии.
Вязкость
Вязкость — это свойство жидкости, которое измеряет сопротивление жидкости деформации из-за силы сдвига.Вязкость — это внутреннее трение жидкости, которое заставляет ее сопротивляться протеканию мимо твердой поверхности или других слоев жидкости. Вязкость также можно рассматривать как меру сопротивления жидкости течению. Густое масло имеет высокую вязкость; вода имеет низкую вязкость. Единица измерения абсолютной вязкости:
µ = абсолютная вязкость жидкости (фунт-сила-сек / фут2).
Вязкость жидкости обычно существенно зависит от температуры жидкости и относительно не зависит от давления.Для большинства жидкостей, когда температура жидкости увеличивается, вязкость жидкости уменьшается. Пример этого можно увидеть в смазочном масле двигателей. Когда двигатель и его смазочное масло холодные, масло очень вязкое или густое. После запуска двигателя и повышения температуры смазочного масла вязкость масла значительно снижается, и масло кажется намного более жидким.
Идеальная жидкость
Идеальная жидкость — это несжимаемая жидкость без вязкости. Идеальных жидкостей на самом деле не существует, но иногда полезно рассмотреть, что случилось бы с идеальной жидкостью в конкретной задаче потока жидкости, чтобы упростить задачу.
Идеальных жидкостей на самом деле не существует, но иногда полезно рассмотреть, что случилось бы с идеальной жидкостью в конкретной задаче потока жидкости, чтобы упростить задачу.
Число Рейнольдса
Режим потока (ламинарный или турбулентный) определяется путем оценки числа Рейнольдса потока (см. Рисунок 5). Число Рейнольдса, основанное на исследованиях Осборна Рейнольдса, представляет собой безразмерное число, состоящее из физических характеристик потока. Уравнение 3-7 используется для расчета числа Рейнольдса (N R ) для потока жидкости.
N
R = PvD / мкг c (3-7)где:
N R = число Рейнольдса (без единицы измерения)
v = средняя скорость (фут / сек)
D = диаметр трубы (футы)
µ = абсолютная вязкость жидкости (фунт-сила-сек / фут2)
ρ = массовая плотность жидкости (фунт / фут3)
г c = гравитационная постоянная (32,2 фут-фунт-сила / фунт-сила-сек2) )
Для практических целей, если число Рейнольдса меньше 2000, поток является ламинарным.Если оно больше 3500, поток турбулентный. Потоки с числами Рейнольдса от 2000 до 3500 иногда называют переходными. Большинство жидкостных систем на ядерных установках работают с турбулентным потоком. Числа Рейнольдса можно удобно определить с помощью диаграммы Moody Chart; пример которого приведен в Приложении B. Дополнительные сведения об использовании диаграммы Moody Chart представлены в последующем тексте.
Основные положения этой главы кратко изложены ниже.
• Ламинарный поток Слои воды текут друг над другом с разной скоростью, практически без перемешивания между слоями.Профиль скорости потока для ламинарного потока в круглых трубах имеет параболическую форму с максимальным потоком в центре трубы и минимальным потоком на стенках трубы. Средняя скорость потока составляет примерно половину максимальной скорости.
• Турбулентный поток Поток характеризуется неравномерным движением частиц жидкости. Профиль скорости турбулентного потока довольно плоский в центральной части трубы и быстро падает очень близко к стенкам.Средняя скорость потока примерно равна скорости в центре трубы.
Профиль скорости турбулентного потока довольно плоский в центральной части трубы и быстро падает очень близко к стенкам.Средняя скорость потока примерно равна скорости в центре трубы.
• Вязкость — это свойство жидкости, которое измеряет сопротивление жидкости деформации из-за силы сдвига. Для большинства жидкостей температура и вязкость обратно пропорциональны.
• Идеальная жидкость — это несжимаемая жидкость без вязкости.
• Увеличение числа Рейнольдса указывает на усиление турбулентности потока.
Общее уравнение энергии
Принцип сохранения энергии гласит, что энергия не может быть ни создана, ни разрушена.Это эквивалентно Первому закону термодинамики, который использовался для разработки общего уравнения энергии в модуле по термодинамике. Уравнение 3-8 представляет собой формулировку общего уравнения энергии для открытой системы.
Q + (U + PE + KE + PV) в =
W + (U + PE + KE + PV)
из + (U + PE + KE + PV) сохранено (3-8 )где:
Q = тепло (британские тепловые единицы)
U = внутренняя энергия (британские тепловые единицы)
PE = потенциальная энергия (фут-фунт-сила)
KE = кинетическая энергия (фут-фунт-сила)
P = давление ( фунт-сила / фут 2 )
V = объем (фут 3 )
W = работа (фут-фунт-сила)
Упрощенное уравнение Бернулли
Уравнение Бернулли является результатом применения общего уравнения энергии и первого закона термодинамики к системе с установившимся потоком, в которой никакая работа не выполняется с флюидом или с помощью текучей среды, тепло не передается к текучей среде или от нее, и не происходит никаких изменений внутренней энергии (т.е., без изменения температуры) жидкости. В этих условиях общее уравнение энергии упрощается до уравнения 3-9.
(PE + KE + PV)
1 = (PE + KE + PV) 2 (3-9) Подставив соответствующие выражения для потенциальной энергии и кинетической энергии, уравнение 3-9 можно переписать как Equation 3-10.
mgz
1/ g c + mv 1 2/ 2g c + P 1 V 1 = mgz 904 + mv 2 2/ 2g c + P 2 V 2 (3-10)где:
m = масса (фунт-метр)
z = высота над ссылка (фут)
v = средняя скорость (фут / сек)
g = ускорение свободного падения (32.17 фут / сек 2 )
gc = гравитационная постоянная, (32,17 фут-фунт / фунт-сила-сек 2 )
Примечание: коэффициент g c требуется только при использовании английской системы измерения и Масса измеряется в фунтах массы. По сути, это коэффициент преобразования, необходимый для непосредственного вывода единиц измерения. Нет необходимости в множителе, если масса измеряется в пробках или если используется метрическая система измерения.
Каждый член в уравнении 3-10 представляет форму энергии, которой обладает движущаяся жидкость (потенциальная, кинетическая энергия и энергия, связанная с давлением).По сути, уравнение физически представляет собой баланс энергий KE, PE, PV, так что если одна форма энергии увеличивается, одна или несколько других уменьшаются, чтобы компенсировать, и наоборот.
Умножение всех членов в уравнении 3-10 на коэффициент gc / mg дает форму уравнения Бернулли, показанного уравнением 3-11.
z
1 + v 1 2 / 2g + P 1 ν 1 g c / g = z 2 + v 2 2 / 2g + P 2 ν 2 г c / г (3-11)Напор
Поскольку единицы для всех различных форм энергии в уравнении 3-11 измеряются в единицах расстояния, эти термины иногда называют «Напоры» (напор, напор скорости и напор).Термин «напор» используется инженерами применительно к давлению. Это ссылка на высоту, обычно в футах, водяного столба, который будет выдерживать данное давление. Каждую из энергий, которыми обладает жидкость, можно выразить через голову. Высота напора представляет потенциальную энергию жидкости из-за ее возвышения над контрольным уровнем. Скоростной напор представляет собой кинетическую энергию жидкости. Это высота в футах, на которую текущая жидкость поднялась бы в столбе, если бы вся ее кинетическая энергия была преобразована в потенциальную.Напор представляет собой энергию потока столба жидкости, вес которой эквивалентен давлению жидкости.
Каждую из энергий, которыми обладает жидкость, можно выразить через голову. Высота напора представляет потенциальную энергию жидкости из-за ее возвышения над контрольным уровнем. Скоростной напор представляет собой кинетическую энергию жидкости. Это высота в футах, на которую текущая жидкость поднялась бы в столбе, если бы вся ее кинетическая энергия была преобразована в потенциальную.Напор представляет собой энергию потока столба жидкости, вес которой эквивалентен давлению жидкости.
Сумма подъемного напора, скоростного напора и напора жидкости называется общим напором. Таким образом, уравнение Бернулли утверждает, что общий напор жидкости постоянен.
Преобразование энергии в жидкостных системах
Уравнение Бернулли позволяет легко исследовать, как происходит передача энергии между вертикальным, скоростным и напорным напором.Можно исследовать отдельные компоненты трубопроводных систем и определить, какие свойства жидкости изменяются и как это влияет на энергетический баланс.
Если труба, содержащая идеальную жидкость, подвергается постепенному расширению в диаметре, уравнение неразрывности говорит нам, что по мере увеличения диаметра и площади проходного сечения скорость потока должна уменьшаться, чтобы поддерживать тот же массовый расход. Поскольку скорость на выходе меньше скорости на входе, скоростной напор потока должен уменьшаться от входа к выходу.Если труба лежит горизонтально, напор не меняется; следовательно, уменьшение скоростного напора должно быть компенсировано увеличением напора. Поскольку мы рассматриваем идеальную несжимаемую жидкость, удельный объем жидкости не изменится. Единственный способ увеличения напора несжимаемой жидкости — это увеличение давления. Таким образом, уравнение Бернулли показывает, что уменьшение скорости потока в горизонтальной трубе приведет к увеличению давления.
Если труба постоянного диаметра, содержащая идеальную жидкость, подвергается уменьшению отметки, результат будет таким же, но по разным причинам. В этом случае скорость потока и скоростной напор должны быть постоянными, чтобы удовлетворять уравнению неразрывности массы.
В этом случае скорость потока и скоростной напор должны быть постоянными, чтобы удовлетворять уравнению неразрывности массы.
Таким образом, уменьшение напора можно компенсировать только увеличением напора. Опять же, жидкость несжимаема, поэтому увеличение напора должно приводить к увеличению давления.
Несмотря на то, что уравнение Бернулли имеет несколько ограничений, существует множество задач с физической жидкостью, к которым оно применяется.Как и в случае сохранения массы, уравнение Бернулли может применяться к задачам, в которых более одного потока могут одновременно входить в систему или выходить из нее. Особо следует отметить тот факт, что задачи последовательной и параллельной системы трубопроводов решаются с помощью уравнения Бернулли.
Пример: уравнение БернуллиПредположим, что поток без трения в длинной горизонтальной конической трубе. Диаметр составляет 2,0 фута на одном конце и 4,0 фута на другом. Напор на меньшем конце составляет 16 футов водяного столба.Если вода течет через этот конус со скоростью 125,6 фут3 / сек, найдите скорости на двух концах и напор на большем конце.
Решение:
V˙ 1 = A 1 v 1
v 1 = V˙ 1 / A 1 v 2 = 904 2 / A 2
v 1 = 125.6 футов 3 / сек / π (1 фут) 2 v 2 = 125,6 футов 3 / сек / π (2 фута) 2
v 1 = 40 футов / с v 2 = 10 футов / с
z 1 + v 1 2 / 2g + P 1 ν 1 g c / g = z 2 + v 2 2 / 2g + P 2 ν 2 g c / g
P 2 ν 2 g c / g = P 1 ν 1 g c / g + (z 1 — z 2 ) + (v 1 2 — v 2 2 ) / 2g
= 16 футов + 0 футов + [(40 футов / сек) 2 — (10 футов / сек) 2 /2 (32.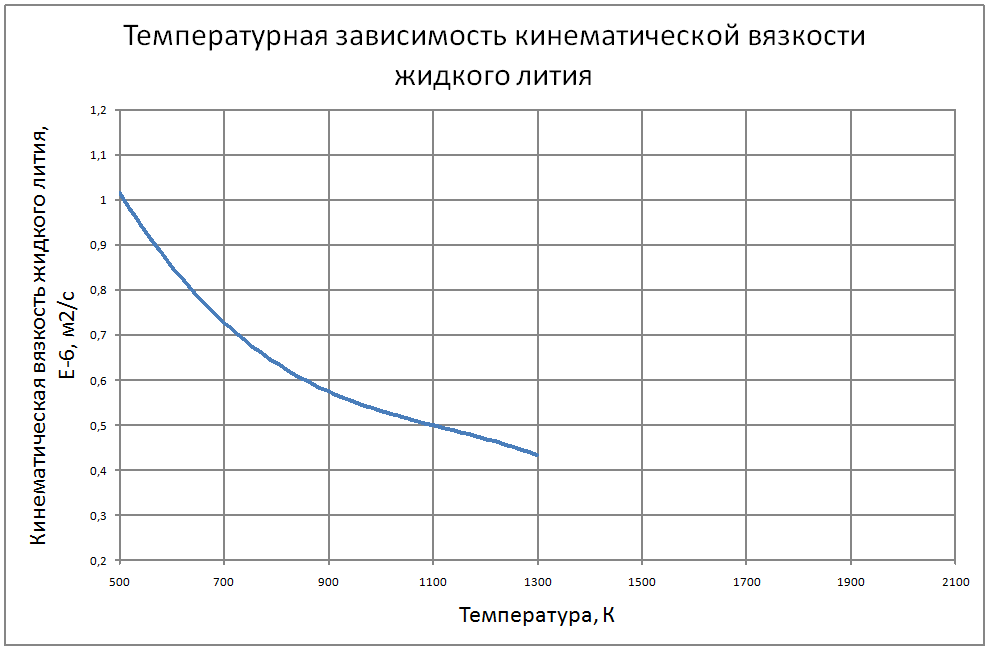 17 фут-фунт-сила / фунт-сила — сек 2 )]
17 фут-фунт-сила / фунт-сила — сек 2 )]
= 39,3 фута
Ограничения упрощенного уравнения Бернулли
Практическое применение упрощенного уравнения Бернулли к реальным трубопроводным системам невозможно из-за двух ограничений. Одно серьезное ограничение уравнения Бернулли в его нынешней форме состоит в том, что трение жидкости недопустимо при решении проблем трубопроводов. Следовательно, уравнение 3-10 применимо только к идеальным жидкостям. Однако в действительности общий напор жидкости не может быть полностью перенесен из одной точки в другую из-за трения.Учет этих потерь напора даст гораздо более точное описание того, что происходит физически. Это особенно верно, потому что одна из задач насоса в гидравлической системе — преодоление потерь давления из-за трения трубы.
Второе ограничение в уравнении Бернулли состоит в том, что нельзя выполнять какую-либо работу с жидкостью или с ней. Это ограничение предотвращает анализ двух точек в потоке жидкости, если между двумя точками существует насос. Поскольку большинство проточных систем включает насосы, это существенное ограничение.К счастью, упрощенное уравнение Бернулли можно модифицировать таким образом, чтобы удовлетворительно учитывать потери напора и работу насоса.
Расширенное Бернулли
Уравнение Бернулли можно модифицировать, чтобы учесть прирост и потерю напора. Полученное уравнение, называемое расширенным уравнением Бернулли, очень полезно при решении большинства задач потока жидкости. Фактически, расширенное уравнение Бернулли, вероятно, используется больше, чем любое другое уравнение потока жидкости. Уравнение 3-12 является одной из форм расширенного уравнения Бернулли.
z
1 + v 1 2 / 2g + P 1 ν 1 g c / g + H p = z 2 + v 2 2 / 2g + P 2 ν 2 g c / g + H f (3-12)где:
z = высота над исходным уровнем (футы)
v = средняя скорость жидкости ( фут / сек)
P = давление жидкости (фунт-сила / фут 2 )
ν = удельный объем жидкости (фут 3 / фунт)
л. с. = напор, добавляемый насосом (фут)
с. = напор, добавляемый насосом (фут)
Hf = потеря напора из-за гидравлического трения (футы)
g = ускорение свободного падения (фут / сек 2 )
Потеря напора из-за гидравлического трения (Hf) представляет собой энергию, используемую для преодоления трения, вызванного стенками трубка.Хотя это представляет собой потерю энергии с точки зрения потока текучей среды, обычно это не означает значительную потерю общей энергии текучей среды. Это также не нарушает закон сохранения энергии, поскольку потеря напора из-за трения приводит к эквивалентному увеличению внутренней энергии (u) жидкости. Эти потери являются наибольшими, когда жидкость протекает через входы, выходы, насосы, клапаны, фитинги и любые другие трубопроводы с шероховатой внутренней поверхностью.
Большинство методов оценки потери напора из-за трения являются эмпирическими (основанными почти исключительно на экспериментальных данных) и основаны на константе пропорциональности, называемой коэффициентом трения (f), который будет обсуждаться в следующем разделе.
Пример: Extended BernoulliВода перекачивается из большого резервуара в точку на 65 футов выше резервуара. Сколько футов напора должно быть добавлено насосом, если через 6-дюймовую трубу проходит 8000 фунтов / час, а потеря напора на трение составляет 2 фута? Плотность жидкости составляет 62,4 фунта / фут3, а площадь поперечного сечения 6-дюймовой трубы составляет 0,2006 фута 2 .
Решение:
Чтобы использовать модифицированную форму уравнения Бернулли, ориентиры выбираются на поверхности резервуара (точка 1) и на выходе из трубы (точка 2).Давление на поверхности резервуара такое же, как давление на выходе из трубы, то есть атмосферное давление. Скорость в точке 1 будет практически равна нулю.
Использование уравнения массового расхода для определения скорости в точке 2:
м˙ 2 = ρ A 2 v 2
v 2 = m˙ 2 / ρ A
v 2 = 0. 178 фут / с
178 фут / с
z 1 + v 1 2 / 2g + P 1 ν 1 g c / g + H p = z 2 + v 2 2 / 2g + P 2 ν 2 g c / g + H f
H p = (z 2 — z 1 ) + (v 2 2 — v 1 2 ) / 2g + (P 2 — P 1 ) ν (g c / g) + H f
H p = 65 футов + [(0.178 фут / сек) 2 — (фут / сек) 2 ] / [2 (32,17 фут-фунт / фунт-сила-сек 2 )] + 0 футов + 2 фута
H p = 67 футов [/ box]
Следует отметить, что решение этой примерной задачи имеет числовое значение, которое «имеет смысл» из данных, приведенных в задаче. Общее увеличение напора на 67 футов в основном связано с увеличением оценки на 65 футов и увеличением напора трения на 2 фута.
Применение уравнения Бернулли к трубке Вентури
Многие компоненты установки, такие как трубка Вентури, могут быть проанализированы с использованием уравнения Бернулли и уравнения неразрывности.Вентури — это устройство для измерения расхода, которое состоит из постепенного сжатия с последующим постепенным расширением. Пример трубки Вентури показан на рисунке 6. Измеряя перепад давления между входом трубки Вентури (точка 1) и горловиной трубки Вентури (точка 2), можно определить скорость потока и массовый расход на основе формулы Бернулли. уравнение.
Рис. 6. Измеритель Вентури Уравнение Бернулли утверждает, что общий напор потока должен быть постоянным. Так как высота не изменяется существенно, если вообще не изменяется между точками 1 и 2, высота напора в этих двух точках будет по существу одинакова и будет исключена из уравнения.Таким образом, уравнение Бернулли упрощается до уравнения 3-13 для трубки Вентури.
v
1 2 / 2g + P 1 ν 1 g c / g = v 2 2 / 2g + P 2 ν 2 g c / g (3-13)Применение уравнения неразрывности к точкам 1 и 2 позволяет нам выразить скорость потока в точке 1 как функцию скорости потока в точке 2 и отношения двух областей потока.
ρ 1 A 1 v 1 = ρ 2 A 2 v 2
v 1 = ρ 2 A 2 v 904 1 / A 1
v 1 = v 2 A 2 / A 1
Использование алгебры для преобразования уравнения 3-13 и замена полученного выше результата на v 1 позволяет нам решить для Версия 2 .
v 2 2 — v 1 2 / 2g = (P 1 –P 2 ) ν g c / g
v 2 2 — (v 2 A 2 / A 1 ) 2 = (P 1 — P 2 ) 2 ν g c
v 2 2 (1 — (A 2 / A 1 ) 2 ) = (P 1 — P 2 ) 2 ν g c
v 2 2 = (P 1 — P 2 ) 2 ν g c / (1 — (A2 / A1) 2 )
v 2 = √ [(P 1 — P 2 ) 2 ν g c / (1 — (A2 / A1) 2 )]
v 2 = √ (P 1 — P 2 ) √ [2 ν g c / (1 — (A2 / A1) 2 )]
Следовательно, скорость потока в горловине трубки Вентури и объемный расход являются прямыми y пропорционально квадратному корню из перепада давления.
Давления на участке выше по потоку и в горловине являются фактическими давлениями, а скорости из уравнения Бернулли без потерь являются теоретическими скоростями.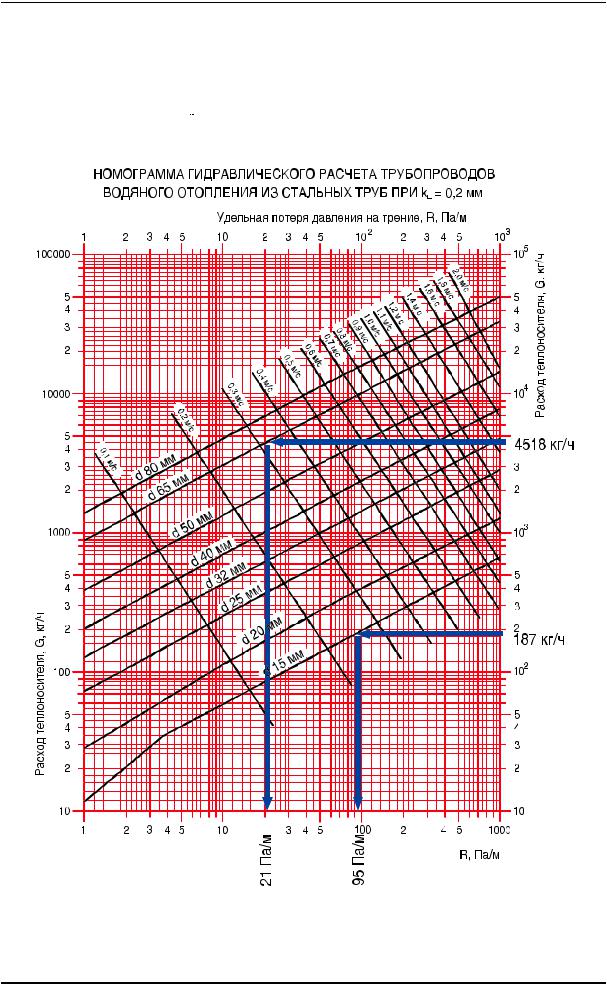 Когда потери учитываются в уравнении энергии, скорости являются фактическими скоростями. Во-первых, с помощью уравнения Бернулли (то есть без члена потери напора) получается теоретическая скорость в горловине. Затем умножив это на коэффициент Вентури (C v ), который учитывает потери на трение и равен 0.98 для большинства Вентури получается фактическая скорость. Фактическая скорость, умноженная на фактическую площадь горловины, определяет фактический объемный расход нагнетания.
Когда потери учитываются в уравнении энергии, скорости являются фактическими скоростями. Во-первых, с помощью уравнения Бернулли (то есть без члена потери напора) получается теоретическая скорость в горловине. Затем умножив это на коэффициент Вентури (C v ), который учитывает потери на трение и равен 0.98 для большинства Вентури получается фактическая скорость. Фактическая скорость, умноженная на фактическую площадь горловины, определяет фактический объемный расход нагнетания.
Падение давления P 1 — P 2 через трубку Вентури можно использовать для измерения расхода с помощью U-образного манометра, как показано на рисунке 6. Показание R ‘манометра пропорционально падению давления и, следовательно, скорости жидкости.
Основные положения этой главы кратко изложены ниже.
• Краткое изложение уравнения Бернулли
• Уравнение Бернулли является приложением Первого закона термодинамики.
• Уравнение Бернулли представляет собой приложение общего уравнения энергии к системе с установившимся потоком, в которой никакая работа не выполняется с жидкостью или с жидкостью, тепло не передается к жидкости или от нее, и не происходит никаких изменений внутренней энергии жидкости.
• Напор — это термин, используемый для описания давления, оказываемого на жидкость или со стороны жидкости.
• Поскольку жидкость течет в системе трубопроводов, изменения высоты, скорости и напора должны быть согласованными, чтобы удовлетворялось уравнение Бернулли.
• Уравнение Бернулли можно модифицировать, чтобы учесть потери на трение и работу насоса.
• Трубка Вентури может использоваться для определения массового расхода из-за изменений давления и скорости жидкости.
• Объемный расход через трубку Вентури прямо пропорционален квадратному корню из перепада давления между входом трубки Вентури и ее горловиной.
Потеря напора
Потеря напора — это мера уменьшения общего напора (сумма подъемного напора, скоростного напора и напора) жидкости при ее движении через жидкостную систему. В реальных жидкостях потеря напора неизбежна. Это происходит из-за: трения между жидкостью и стенками трубы; трение между соседними частицами жидкости при их движении относительно друг друга; и турбулентность, вызываемая всякий раз, когда поток перенаправляется или каким-либо образом влияет на такие компоненты, как входы и выходы трубопроводов, насосы, клапаны, редукторы потока и фитинги.
Потери на трение — это часть общей потери напора, которая возникает, когда жидкость течет по прямым трубам. Потеря напора для потока жидкости прямо пропорциональна длине трубы, квадрату скорости жидкости и члену, учитывающему трение жидкости, называемому коэффициентом трения. Потеря напора обратно пропорциональна диаметру трубы.
Потеря напора ∝ f Lv 2 / D
Коэффициент трения
Коэффициент трения, как было установлено, зависит от числа Рейнольдса для потока и степени шероховатости внутренней поверхности трубы.
Величина, используемая для измерения шероховатости трубы, называется относительной шероховатостью, которая равна средней высоте неровностей поверхности (ε), деленной на диаметр трубы (D).
Относительная шероховатость = ε / D
Значение коэффициента трения обычно получают из диаграммы Moody Chart (Рисунок A). Диаграмму Moody Chart можно использовать для определения коэффициента трения на основе числа Рейнольдса и относительной шероховатости.
Рисунок A: Moody Chart Пример:Определите коэффициент трения (f) для потока жидкости в трубе с числом Рейнольдса 40 000 и относительной шероховатостью 0.01.
Решение:
Используя диаграмму Moody Chart, число Рейнольдса 40 000 пересекает кривую, соответствующую относительной шероховатости 0,01 при коэффициенте трения 0,04.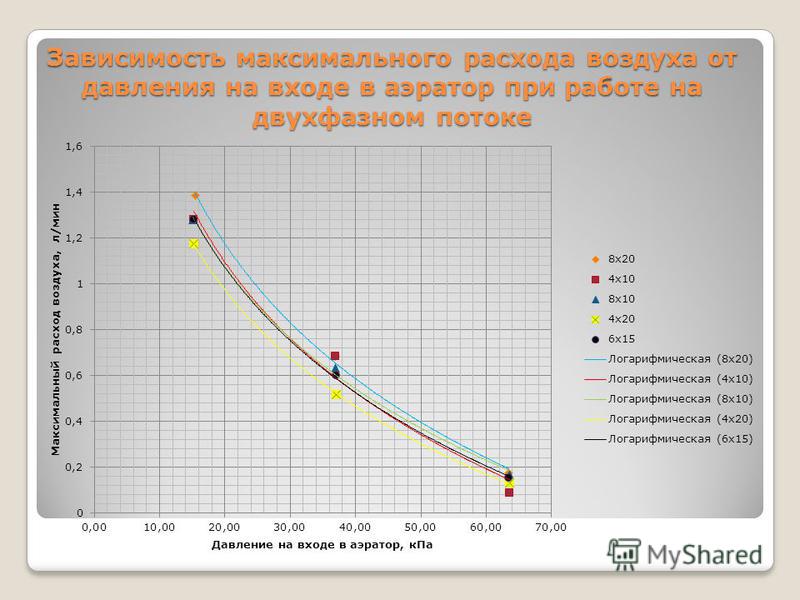
Уравнение Дарси
Потери напора на трение могут быть рассчитаны с использованием математической зависимости, известной как уравнение Дарси для потери напора. Уравнение принимает две различные формы. Первая форма уравнения Дарси определяет потери в системе, связанные с длиной трубы.
H
r = f L v 2 / D 2 g (3-14)где:
f = коэффициент трения (без агрегата)
L = длина трубы (футы)
D = диаметр длины трубы (футы)
v = скорость жидкости (фут / сек)
g = ускорение свободного падения (фут / сек 2 )
Пример:Уравнение потери напора Дарси Труба длиной 100 футов и диаметром 20 дюймов содержит воду при температуре 200 ° F, текущую с массовым расходом 700 фунтов / м3.Вода имеет плотность 60 фунтов / фут 3 и вязкость 1,978 x 10 -7 фунт-сила-сек / фут 2 . Относительная шероховатость трубы 0,00008. Рассчитайте потерю напора для трубы.
Решение:
Последовательность шагов, необходимых для решения этой проблемы, состоит в том, чтобы сначала определить скорость потока. Во-вторых, используя скорость потока и заданные свойства жидкости, вычислите число Рейнольдса. В-третьих, определите коэффициент трения по числу Рейнольдса и относительной шероховатости.Наконец, используйте уравнение Дарси, чтобы определить потерю напора.
m˙ = ρ A v
v = m˙ / ρ A
= (700 фунт / сек) / (60 фунт / фут 3 ) π (10 дюймов) 2 (1 фут 2 / 144 дюйма 2)
v = 5,35 фут / сек
N R = ρ v D / мкг c
N R = (60 фунтов / фут 3 ) (5,35 футов / с) (20 дюймов) (1 фут / 12 дюймов) / (1,978 x 10 -7 фунт-сила-с / фут 2 ) (32,17 фут-фунт-сила / фунт-сила-фут-с 2) =
N R = 8.4 x 10 7
Используйте диаграмму Moody для числа Рейнольдса 8,4 x 10 7 и относительной шероховатости 0,00008.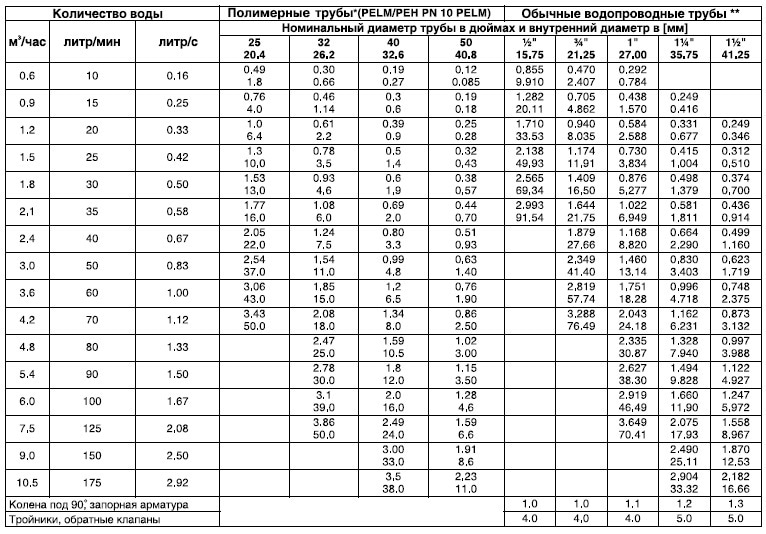
f = 0,012
H f = f (L / D) (v 2 / 2g)
H f = (o.o12) [100 футов / (20 дюймов) (1 фут / 12 дюймов) )] * (5,35 фут / сек) 2 /(2)(32,17 фут / сек 2 )
H f = 0,32 фута
Незначительные потери
Потери, возникающие в трубопроводах из-за изгибов, локти, суставы, клапаны и т. д.иногда называют незначительными потерями. Это неправильное название, потому что во многих случаях эти потери более важны, чем потери из-за трения трубы, рассмотренные в предыдущем разделе. Для всех незначительных потерь в турбулентном потоке потеря напора изменяется пропорционально квадрату скорости. Таким образом, удобный метод выражения незначительных потерь потока — это коэффициент потерь (k). Значения коэффициента потерь (k) для типовых ситуаций и арматуры можно найти в стандартных справочниках. Форма уравнения Дарси, используемого для расчета незначительных потерь отдельных компонентов жидкостной системы, выражается уравнением 3-15.
H
f = kv 2 / 2g (3-15)Эквивалентная длина трубопровода
Незначительные потери могут быть выражены через эквивалентную длину (Leq) трубы, которая будет иметь такую же потерю напора для такая же скорость нагнетаемого потока. Эту взаимосвязь можно найти, установив две формы уравнения Дарси равными друг другу.
f L v 2 / D 2g = kv 2 / 2g
Это дает два полезных соотношения
L
eq = k D / f (3-16)k = f L
eq / D (3-17) Типичные значения L eq / D для общих компонентов трубопроводной системы перечислены в таблице 1.Эквивалентная длина трубопровода, которая вызовет такую же потерю напора, как и конкретный компонент, может быть определена путем умножения значения L экв. / D для этого компонента на диаметр трубы. Чем выше значение L eq / D, тем длиннее эквивалентная длина трубы.
Полностью открытая задвижка находится в трубе диаметром 10 дюймов. Какая эквивалентная длина трубы вызовет такую же потерю напора, как и задвижка?
Решение:
Из таблицы 1 мы находим, что значение L экв. / D для полностью открытой задвижки равно 10.
L eq = (L / D) D
= 10 (10 дюймов)
= 100 дюймов
Добавляя эквивалентные длины всех компонентов к фактической длине трубы в системе, мы можем получить L экв. значение для всей системы трубопроводов.
Основные положения этой главы кратко изложены ниже.
• Потеря напора — это уменьшение общего напора (сумма потенциального напора, скоростного напора и напора) жидкости, вызванное трением, присутствующим при движении жидкости.
• Потери на трение — это часть общей потери напора, возникающая при протекании жидкости по прямым трубам.
• Незначительные потери — это потери напора, возникающие из-за изгибов, колен, соединений, клапанов и других компонентов. Каждый раз, когда поток изменяет направление или изменяется площадь поперечного сечения, он испытывает потерю напора.
• Коэффициент трения для потока жидкости можно определить с помощью диаграммы Moody Chart, если можно определить относительную шероховатость трубы и число Рейнольдса потока.
• Уравнение Дарси можно использовать для расчета потерь на трение.
• Для расчета незначительных потерь можно использовать специальную форму уравнения Дарси.
• Длину трубы, которая может вызвать такую же потерю напора, как у клапана или фитинга, можно определить, умножив значение L / D для компонента, указанного в справочниках или руководствах поставщиков, на диаметр трубы.
Принудительная и естественная циркуляция
В предыдущих главах, посвященных потоку жидкости, было объяснено, что каждый раз, когда жидкость течет, возникает некоторое трение, связанное с движением, которое вызывает потерю напора. Было отмечено, что эта потеря напора обычно компенсируется в системах трубопроводов насосами, которые действительно работают с жидкостью, компенсируя потерю напора из-за трения. Циркуляция жидкости в системах с помощью насосов обозначается как принудительная циркуляция .
Было отмечено, что эта потеря напора обычно компенсируется в системах трубопроводов насосами, которые действительно работают с жидкостью, компенсируя потерю напора из-за трения. Циркуляция жидкости в системах с помощью насосов обозначается как принудительная циркуляция .
Некоторые жидкостные системы можно спроектировать таким образом, чтобы не было необходимости в насосах для обеспечения циркуляции. Напор, необходимый для компенсации потерь напора, создается градиентами плотности и перепадами высоты.Поток, возникающий в этих условиях, называется естественной циркуляцией .
Тепловая приводная головка
Тепловая приводная головка — это сила, которая вызывает естественную циркуляцию. Это вызвано разницей в плотности между двумя телами или областями жидкости.
Рассмотрим два равных объема жидкости одного и того же типа. Если два объема имеют разную температуру, тогда объем с более высокой температурой также будет иметь меньшую плотность и, следовательно, меньшую массу.Поскольку объем при более высокой температуре будет иметь меньшую массу, на него также будет оказываться меньшая сила тяжести. Эта разница в силе тяжести, действующей на жидкость, будет приводить к тому, что более горячая жидкость поднимается, а более холодная жидкость опускается.
Этот эффект наблюдается во многих местах. Один из примеров — воздушный шар. Сила, заставляющая воздушный шар подниматься вверх, является результатом разницы в плотности между горячим воздухом внутри воздушного шара и более холодным воздухом, окружающим его.
Тепло, добавляемое воздуху в воздушном шаре, добавляет энергию молекулам воздуха. Движение молекул воздуха увеличивается, и молекулы воздуха занимают больше места. Молекулы воздуха внутри воздушного шара занимают больше места, чем такое же количество молекул воздуха вне воздушного шара. Это означает, что горячий воздух менее плотный и легкий, чем окружающий воздух. Поскольку воздух в воздушном шаре менее плотный, сила тяжести оказывает на него меньшее влияние. В результате воздушный шар весит меньше окружающего воздуха.Гравитация втягивает более холодный воздух в пространство, занимаемое воздушным шаром. Движение более холодного воздуха вниз выталкивает воздушный шар из ранее занятого пространства, и он поднимается.
В результате воздушный шар весит меньше окружающего воздуха.Гравитация втягивает более холодный воздух в пространство, занимаемое воздушным шаром. Движение более холодного воздуха вниз выталкивает воздушный шар из ранее занятого пространства, и он поднимается.
Условия, необходимые для естественной циркуляции
Естественная циркуляция будет иметь место только при наличии правильных условий. Даже после того, как естественное кровообращение началось, устранение любого из этих условий приведет к остановке естественного кровообращения. Условия естественной циркуляции следующие.
1. Существует разница температур (имеется источник тепла и радиатор).
2. Источник тепла находится ниже радиатора.
3. Жидкости должны контактировать друг с другом.
Должны быть два тела жидкости с разными температурами. Это также может быть одно жидкое тело с участками с разной температурой. Разница в температуре необходима для разницы в плотности жидкости. Разница в плотности является движущей силой естественного циркуляционного потока.
Для продолжения естественной циркуляции необходимо поддерживать разницу температур. Добавление тепла от источника тепла должно происходить в зоне с высокой температурой. В области низких температур должен существовать непрерывный отвод тепла радиатором. В противном случае температуры в конечном итоге выровнялись бы и дальнейшая циркуляция прекратилась.
Источник тепла должен располагаться ниже радиатора. Как показано на примере воздушного шара, более теплая жидкость менее плотна и имеет тенденцию подниматься, а более холодная жидкость более плотная и имеет тенденцию опускаться.Чтобы воспользоваться преимуществом естественного движения теплых и холодных жидкостей, источник тепла и радиатор должны располагаться на соответствующей высоте.
Две области должны соприкасаться, чтобы был возможен поток между ними. Если путь потока заблокирован или заблокирован, естественная циркуляция невозможна.
Пример охлаждения с естественной циркуляцией
Естественная циркуляция часто является основным средством охлаждения реакторов бассейнового типа и облученных тепловыделяющих сборок, хранящихся в бассейнах с водой после извлечения из реактора. Источником тепла является тепловыделяющая сборка. Радиатор — это основная часть воды в бассейне.
Источником тепла является тепловыделяющая сборка. Радиатор — это основная часть воды в бассейне.
Вода в нижней части тепловыделяющей сборки поглощает энергию, генерируемую сборкой. Температура воды увеличивается, а плотность уменьшается. Сила тяжести втягивает более холодную (более плотную) воду в нижнюю часть узла, вытесняя более теплую воду. Более теплая (более легкая) вода вынуждена уступить свое место более холодной (более тяжелой) воде. Более теплая (более легкая) вода поднимается выше в сборке. По мере продвижения воды по длине сборки она поглощает больше энергии.Вода становится все светлее и светлее, непрерывно выталкиваясь вверх более плотной водой, движущейся под ней. В свою очередь, более холодная вода поглощает энергию от узла и также вынуждена подниматься по мере продолжения естественного циркуляционного потока. Вода, выходящая из верхней части топливной сборки, отдает свою энергию, смешиваясь с большей частью воды в бассейне. Основная часть воды в бассейне обычно охлаждается путем циркуляции через теплообменники в отдельном процессе.
Расход и разница температур
Тепловая приводная головка, которая вызывает естественную циркуляцию, возникает из-за изменения плотности, вызванного разницей температур.Как правило, чем больше разница температур между горячей и холодной областями жидкости, тем больше тепловая приводная головка и результирующая скорость потока. Однако рекомендуется держать горячую жидкость переохлажденной, чтобы предотвратить изменение фазы. Можно иметь естественную циркуляцию в двухфазном потоке, но, как правило, поддерживать поток труднее.
Для индикации или проверки естественной циркуляции могут использоваться различные параметры. Это зависит от типа растения.Например, для реактора с водой под давлением (PWR) выбранные параметры системы охлаждения реактора (RCS), которые будут использоваться, следующие.
1. RCS ∆T (T Горячий — T Холодный ) должен составлять 25-80% от значения полной мощности и должен быть постоянным или медленно уменьшаться. Это указывает на то, что остаточное тепло удаляется из системы с достаточной скоростью для поддержания или снижения внутренней температуры.
Это указывает на то, что остаточное тепло удаляется из системы с достаточной скоростью для поддержания или снижения внутренней температуры.
2. RCS Температура горячих и холодных ног должна быть постоянной или медленно снижаться. Опять же, это указывает на то, что тепло удаляется, а тепловая нагрузка распада, как и ожидалось, уменьшается.
3. Давление пара парогенератора (давление вторичного контура) должно соответствовать температуре RCS. Это подтверждает, что парогенератор отводит тепло от охлаждающей жидкости RCS.
Если естественная циркуляция для PWR происходит или неизбежна, можно выполнить несколько действий, чтобы обеспечить или улучшить возможности охлаждения активной зоны. Во-первых, уровень в компенсаторе давления может поддерживаться выше 50%. Во-вторых, поддерживайте переохлаждение RCS на уровне 15 o F или выше.
Оба эти действия помогут предотвратить образование паровых карманов в RCS, где они ограничат поток RCS.В-третьих, поддерживайте уровень воды в парогенераторе ≥ нормального диапазона. Это обеспечивает соответствующий теплоотвод, чтобы гарантировать, что отвод тепла будет достаточным для предотвращения закипания RCS.
Основные положения этой главы перечислены ниже.
• Естественный циркуляционный поток — это циркуляция жидкости без использования механических устройств.
• Принудительный циркуляционный поток — это циркуляция жидкости в системе с помощью насосов.
• Тепловая приводная головка является движущей силой для естественной циркуляции, вызванной разницей в плотности между двумя областями жидкости.
• Для поддержки естественной циркуляции необходимы три элемента:
- Должны быть теплоотвод и источник тепла.
- Источник тепла должен располагаться под радиатором.
- Между теплой и холодной жидкостью должны существовать пути потока.

• Как правило, чем больше разница температур, тем выше расход естественной циркуляции.
• Естественная циркуляция в PWR может быть проверена путем мониторинга:
- RCS ∆T — 25% -80% значение полной мощности
- T Горячий / T Холодный — постоянно или медленно снижение
- Давление пара S / G — отслеживание температуры RCS
• Естественная циркуляция в PWR может быть увеличена за счет:
- поддерживать уровень компенсатора давления> 50%
- поддерживать RCS ≥ 15o F переохлаждение
- поддерживать соответствующий теплоотвод, уровень S / G ≥ нормальный диапазон
Двухфазный поток жидкости
Все отношения потоков жидкости, обсужденные ранее, относятся к потоку одной фазы жидкости, будь то жидкость или пар .В некоторых важных местах в системах потока жидкости происходит одновременный поток жидкой воды и пара, известный как двухфазный поток. Этих простых соотношений, используемых для анализа однофазного потока, недостаточно для анализа двухфазного потока.
Существует несколько методов, используемых для прогнозирования потери напора из-за трения жидкости для двухфазного потока. Трение двухфазного потока больше, чем трение однофазного потока, при тех же размерах трубопровода и массовом расходе. Разница, по-видимому, зависит от типа потока и является результатом увеличения скорости потока.Потери на двухфазное трение экспериментально определяются путем измерения перепада давления на различных элементах трубопровода.
Двухфазные потери обычно связаны с однофазными потерями через те же элементы. Один принятый метод определения потерь на двухфазное трение на основе однофазных потерь включает множитель двухфазного трения (R), который определяется как отношение двухфазных потерь напора к потерям напора, оцененным с использованием насыщенного жидкие свойства.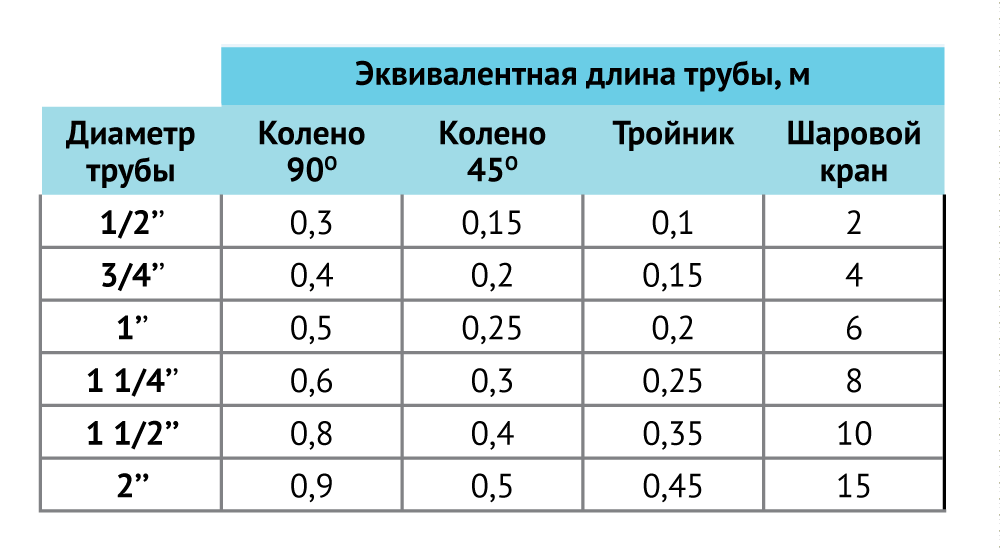
R = H
f, двухфазный / H f, насыщенная жидкость (3-18)где:
R = двухфазный множитель трения (без единиц)
H f, два -фаза = двухфазная потеря напора из-за трения (футы)
H f, насыщенная жидкость = однофазная потеря напора из-за трения (футы)
Множитель трения (R) оказался намного выше при более низких давлениях, чем при более высоких давлениях.Двухфазная потеря напора может быть во много раз больше, чем однофазная потеря напора.
Хотя для моделей двухфазного потока использовалось множество названий, мы определим только три типа потока. Используемые схемы потока определены следующим образом:
1. Пузырьковый поток: происходит рассеяние пузырьков пара в непрерывном потоке жидкости.
2. Пробковый поток: в пузырьковом потоке пузырьки растут за счет слияния и в конечном итоге становятся того же диаметра, что и труба. При этом образуются типичные пузыри пулевидной формы, характерные для снарядного режима.
3. Кольцевой поток: теперь жидкость распределяется между жидкой пленкой, текущей вверх по стенке, и дисперсией капель, текущих в паровом ядре потока.
Нестабильность потока
Нестабильный поток может возникать в виде колебаний потока или его реверсирования. Колебания потока — это изменения потока из-за образования пустот или механических препятствий при проектировании и производстве. Колебания потока в одном канале теплоносителя реактора иногда вызывают колебания потока в окружающих каналах теплоносителя из-за перераспределения потока.Колебания потока нежелательны по нескольким причинам. Во-первых, устойчивые колебания потока могут вызывать нежелательную вынужденную механическую вибрацию компонентов. Это может привести к выходу этих компонентов из строя из-за усталости. Во-вторых, колебания потока могут вызвать проблемы управления системой, имеющие особое значение в ядерных реакторах с жидкостным охлаждением, поскольку теплоноситель также используется в качестве замедлителя. В-третьих, колебания потока влияют на характеристики местного теплообмена и кипения. В ходе испытаний было обнаружено, что критический тепловой поток (CHF), необходимый для отклонения от пузырькового кипения (DNB), может быть снижен на целых 40%, когда поток колеблется.Это сильно снижает тепловой предел и плотность мощности по длине активной зоны реактора. Опять же, посредством испытаний было обнаружено, что колебания потока не являются серьезной проблемой для некоторых реакторов с водой под давлением, если мощность не превышает 150% для нормальных условий потока. Колебания потока могут быть проблемой при работе с естественной циркуляцией из-за присутствующих низких скоростей потока.
В-третьих, колебания потока влияют на характеристики местного теплообмена и кипения. В ходе испытаний было обнаружено, что критический тепловой поток (CHF), необходимый для отклонения от пузырькового кипения (DNB), может быть снижен на целых 40%, когда поток колеблется.Это сильно снижает тепловой предел и плотность мощности по длине активной зоны реактора. Опять же, посредством испытаний было обнаружено, что колебания потока не являются серьезной проблемой для некоторых реакторов с водой под давлением, если мощность не превышает 150% для нормальных условий потока. Колебания потока могут быть проблемой при работе с естественной циркуляцией из-за присутствующих низких скоростей потока.
Во время естественной циркуляции пузырьки пара, образующиеся при колебаниях потока, могут иметь достаточно влияния, чтобы фактически вызвать полное реверсирование потока в затронутом канале.
И колебания потока, и реверсирование потока приводят к очень нестабильному состоянию, поскольку паровые покровы, образующиеся на нагретых поверхностях, напрямую влияют на способность отводить тепло от этих поверхностей.
Штыревой патрубок
В случае разрыва трубы сила реакции, создаваемая высокоскоростной струей жидкости, может вызвать смещение трубопровода и серьезное повреждение компонентов, контрольно-измерительных приборов и оборудования в зоне разрыва. Эта характеристика аналогична необслуживаемому садовому шлангу или пожарному шлангу, который непредсказуемо «хлестает».Этот тип отказа анализируется, чтобы свести к минимуму повреждение, если бы труба изгибалась в непосредственной близости от оборудования, связанного с безопасностью.
Гидравлический удар
Гидравлический удар — это ударная волна жидкости, возникающая в результате внезапного начала или остановки потока. На него влияют начальное давление в системе, плотность жидкости, скорость звука в жидкости, эластичность жидкости и трубы, изменение скорости жидкости, диаметр и толщина трубы и клапана.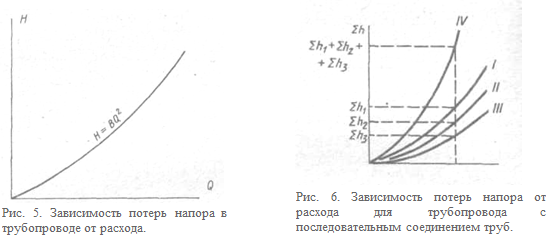 рабочее время.
рабочее время.
Во время закрытия клапана кинетическая энергия движущейся жидкости преобразуется в потенциальную энергию. Эластичность жидкости и стенки трубы создает волну положительного давления, направленную к источнику жидкости. Когда эта волна достигнет источника, масса жидкости будет в покое, но под огромным давлением. Сжатая жидкость и растянутые стенки трубы теперь начнут выпускать жидкость из трубы обратно к источнику и вернуться к статическому давлению источника. Это высвобождение энергии сформирует еще одну волну давления, возвращающуюся к клапану.Когда эта ударная волна достигает клапана, из-за импульса жидкости стенка трубы начинает сокращаться. Это сжатие передается обратно источнику, что снижает давление в трубопроводе ниже статического давления источника. Эти волны давления будут перемещаться вперед и назад несколько раз, пока трение жидкости не демпфирует переменные волны давления до статического давления источника. Обычно весь процесс молота занимает менее одной секунды.
Первоначальный толчок внезапной остановки потока может вызвать переходные изменения давления, превышающие статическое давление.Если клапан закрывается медленно, потеря кинетической энергии будет постепенной. Если его закрыть быстро, потеря кинетической энергии будет очень быстрой. Из-за быстрой потери кинетической энергии возникает ударная волна. Ударная волна, вызванная гидравлическим ударом, может иметь достаточную силу, чтобы вызвать физическое повреждение трубопроводов, оборудования и персонала. Гидравлический удар в трубах, как известно, срывает опоры труб с их креплений, разрывает трубопроводы и вызывает биение труб.
Пик давления
Пик давления — это результирующий быстрый рост давления выше статического, вызванный гидроударами.Максимальный всплеск давления будет в момент изменения расхода и определяется следующим уравнением.
∆P = ρ c ∆v / g c
где:
∆P = скачок давления (фунт-сила / фут 2 )
ρ = плотность жидкости (фунт / фут 3 )
c = Скорость волны давления (фут / сек) (Скорость звука в жидкости)
∆v = Изменение скорости жидкости (фут / сек)
gc = Гравитационная постоянная 32. 17 (фунт-фут / фунт-сила-сек 2 )
17 (фунт-фут / фунт-сила-сек 2 )
Скачок давления Вода с плотностью 62,4 фунт / фут 3 и давлением 120 фунтов на квадратный дюйм течет по трубе со скоростью 10 футов / сек. Скорость звука в воде 4780 футов / сек. Внезапно закрылся обратный клапан. Какое максимальное давление жидкости в фунтах на квадратный дюйм?
Раствор
P Макс. = P статический + ΔP Пик
P Макс. = 120 фунт-сила / дюйм 2 + (62.4 фунта / фут 3 ) (4780 фут / с) (10 фут / с) / (32,17 фунт-фут / фунт-сила с 2 )
P Макс. в 2
P Макс = 76,3 фунтов на кв. дюйм
Паровой молот
Паровой молот похож на гидравлический молот, за исключением того, что он предназначен для паровой системы. Паровой молот — это газовая ударная волна, возникающая в результате внезапного запуска или остановки потока. Паровой молот не так силен, как гидравлический, по трем причинам:
1.Сжимаемость пара гасит ударную волну
2. Скорость звука в паре составляет примерно одну треть скорости звука в воде.
3. Плотность пара примерно в 1600 раз меньше плотности воды.
Проблемы, связанные с паропроводом, включают термический удар и водяные пробки (то есть конденсацию в паровой системе) в результате неправильного нагрева.
Рекомендации по эксплуатации
Гидравлический и паровой молот — не редкость на промышленных предприятиях.Изменения расхода в трубопроводных системах должны производиться медленно, что является частью надлежащей практики оператора. Чтобы предотвратить гидравлический и паровой удар, операторы должны обеспечить надлежащую вентиляцию жидкостных систем и обеспечить надлежащий слив газовых или паровых систем во время запуска. Если возможно, инициируйте запуск насоса при закрытом нагнетательном клапане и медленно откройте нагнетательный клапан, чтобы запустить поток в системе. Если возможно, запускайте насосы меньшей производительности перед насосами большей производительности. По возможности используйте клапаны разогрева вокруг запорных клапанов основного потока.По возможности закройте нагнетательные клапаны насоса перед остановкой насосов. Периодически проверяйте правильность работы влагоуловителей и воздухоотводчиков во время работы.
Если возможно, запускайте насосы меньшей производительности перед насосами большей производительности. По возможности используйте клапаны разогрева вокруг запорных клапанов основного потока.По возможности закройте нагнетательные клапаны насоса перед остановкой насосов. Периодически проверяйте правильность работы влагоуловителей и воздухоотводчиков во время работы.
Основные положения этой главы кратко изложены ниже.
Комбинация жидкости и пара, протекающей по трубе, называется двухфазным потоком.
Типы двухфазного потока включают:
• Пузырьковый поток: происходит диспергирование пузырьков пара в непрерывном потоке жидкости.
• Пробковый поток: пузырьки растут за счет коалесценции и в конечном итоге становятся того же диаметра, что и труба, образуя пузырьки в форме пули.
• Кольцевой поток: жидкость распределяется между жидкой пленкой, текущей вверх по стенке, и дисперсией капель, текущей в паровом ядре потока.
Колебания и нестабильность основного потока могут вызвать:
• нежелательную механическую вибрацию компонентов.
• уменьшение теплового потока, необходимого для возникновения DNB.
• прерывание фактического циркуляционного потока.
Колебания и нестабильность потока могут возникать в следующих условиях:
• сердечник находится вне проектных условий, мощность> 150%
• механический отказ, вызывающий закупорку потока
• недостаточное охлаждение активной зоны во время естественная циркуляция, при которой происходит кипение.
Изгиб трубы — это смещение трубопровода, создаваемое реакционными силами высокоскоростной струи жидкости после разрыва трубы.
Гидравлический удар — это ударная волна жидкости, возникающая в результате внезапного начала или остановки потока.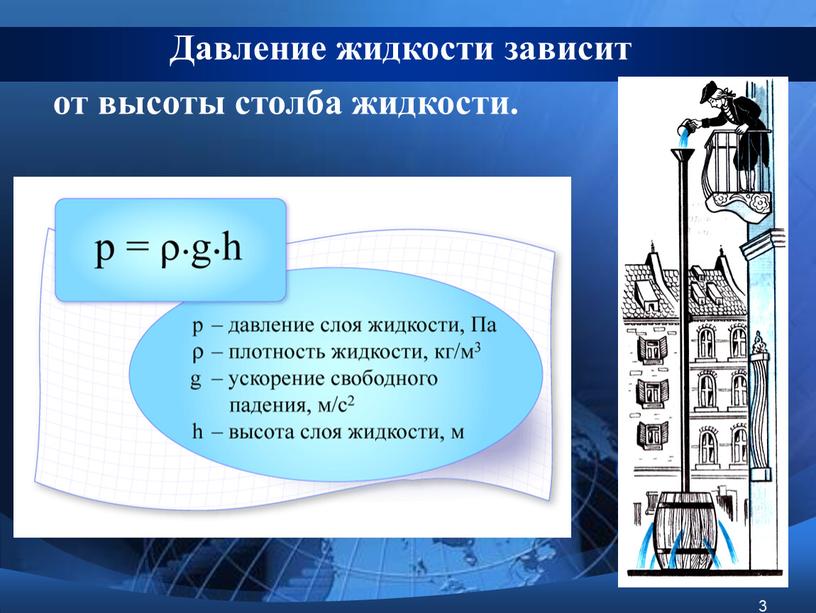
Преобразование энергии в центробежном насосе
Жидкость, поступающая в центробежный насос, сразу же направляется в зону низкого давления в центре или в проушине рабочего колеса. При вращении крыльчатки и лопастей они передают импульс поступающей жидкости. Передача количества движения движущейся жидкости увеличивает скорость жидкости. По мере увеличения скорости жидкости увеличивается ее кинетическая энергия.Жидкость с высокой кинетической энергией вытесняется из области рабочего колеса и попадает в улитку.
Улитка — это область с постоянно увеличивающейся площадью поперечного сечения, предназначенная для преобразования кинетической энергии жидкости в давление жидкости. Механизм этого преобразования энергии такой же, как и для дозвукового потока через расширяющуюся часть сопла. Математический анализ потока через улитку основан на общем уравнении энергии, уравнении неразрывности и уравнении, связывающем внутренние свойства системы.Ключевыми параметрами, влияющими на преобразование энергии, являются увеличивающаяся площадь поперечного сечения улитки, более высокое противодавление системы на выходе улитки и несжимаемый дозвуковой поток жидкости. В результате взаимозависимости этих параметров поток жидкости в улитке, аналогичный дозвуковому потоку в расширяющемся сопле, испытывает уменьшение скорости и увеличение давления.
Рабочие характеристики центробежного насоса
Рис. 7: Типичные характеристики центробежного насоса Кривая Обычно центробежный насос создает относительно небольшое повышение давления в жидкости.Это повышение давления может составлять от нескольких десятков до нескольких сотен фунтов на квадратный дюйм в центробежном насосе с одноступенчатым рабочим колесом. Термин PSID (фунт-сила на квадратный дюйм дифференциала) эквивалентен ∆P. В данном контексте это разница давлений на всасывании и нагнетании насоса. PSID также можно использовать для описания перепада давления в компоненте системы (сетчатые фильтры, фильтры, теплообменники, клапаны, деминерализаторы и т. Д.). Когда центробежный насос работает с постоянной скоростью, увеличение противодавления системы на текущий поток вызывает уменьшение величины объемной скорости потока, которую центробежный насос может поддерживать.
Д.). Когда центробежный насос работает с постоянной скоростью, увеличение противодавления системы на текущий поток вызывает уменьшение величины объемной скорости потока, которую центробежный насос может поддерживать.
Анализ взаимосвязи между объемным расходом (), который центробежный насос V˙ может поддерживать, и перепадом давления в насосе (∆Ppump) основан на различных физических характеристиках насоса и жидкости в системе. Переменные, оцениваемые инженерами-проектировщиками для определения этой взаимосвязи, включают эффективность насоса, мощность, подаваемую на насос, скорость вращения, диаметр рабочего колеса и лопастей, плотность жидкости и вязкость жидкости. Результат этого сложного анализа для типичного центробежного насоса, работающего на одной конкретной скорости, показан на графике на рисунке 7.
Напор насоса по вертикальной оси — это разница между противодавлением в системе и давлением на входе насоса (∆Ppump). Объемный расход (V) по горизонтальной оси — это скорость, с которой жидкость протекает через насос. График предполагает одну конкретную скорость (N) для рабочего колеса насоса.
Кавитация
Когда перекачиваемая жидкость попадает в проушину центробежного насоса, давление значительно снижается. Чем больше скорость потока через насос, тем больше падение давления.Если перепад давления достаточно велик или если температура жидкости достаточно высока, перепад давления может быть достаточным, чтобы заставить жидкость мгновенно превращаться в пар, когда местное давление падает ниже давления насыщения для перекачиваемой жидкости. Эти пузырьки пара перемещаются вдоль рабочего колеса насоса вместе с жидкостью. По мере уменьшения скорости потока давление жидкости увеличивается. Это вызывает внезапное схлопывание пузырьков пара на внешних частях крыльчатки. Образование этих пузырьков пара и их последующее схлопывание — кавитация.
Кавитация может быть очень серьезной проблемой для центробежных насосов. Некоторые насосы могут быть рассчитаны на работу с ограниченным количеством кавитации. Большинство центробежных насосов не могут выдерживать кавитацию в течение значительных периодов времени; они повреждаются из-за эрозии рабочего колеса, вибрации или других проблем, вызванных кавитацией.
Большинство центробежных насосов не могут выдерживать кавитацию в течение значительных периодов времени; они повреждаются из-за эрозии рабочего колеса, вибрации или других проблем, вызванных кавитацией.
Чистый положительный напор на всасывании
Чтобы избежать кавитации во время работы насоса, можно контролировать чистый положительный напор на всасывании насоса.Чистый положительный напор на всасывании (NPSH) для насоса — это разница между давлением всасывания и давлением насыщения перекачиваемой жидкости. NPSH используется для измерения того, насколько жидкость близка к насыщенным условиям. Уравнение 3-19 можно использовать для расчета чистой положительной высоты всасывания, доступной для насоса. Единицы NPSH — футы воды.
NPSH = P
всасывание — P насыщение (3-19)где:
P всасывание = давление всасывания насоса
P насыщение = давление насыщения для жидкости
Путем поддержания доступный NPSH на уровне больше, чем NPSH, требуемый производителем насоса, кавитации можно избежать.
Законы о насосах
Центробежные насосы обычно подчиняются так называемым законам о насосах. Эти законы гласят, что скорость потока или производительность прямо пропорциональны скорости насоса; напор прямо пропорционален квадрату скорости насоса; а мощность, требуемая двигателем насоса, прямо пропорциональна кубу скорости насоса. Эти законы суммированы в следующих уравнениях.
V˙ ∝ n (3-20)
H
P ∝ n 2 (3-21)P ∝ n
3 (3-22)где:
n = скорость рабочее колесо насоса (об / мин)
V = объемный расход насоса (галлонов в минуту или фут3 / час)
H p = напор, развиваемый насосом (фунты на квадратный дюйм или футы)
p = мощность насоса (кВт)
Использование этих пропорциональности, можно разработать уравнения, связывающие условия на одной скорости с условиями на другой скорости.
V˙
1 (n 2 / n 1 ) = V 2 (3-23)H
p1 (n 2 / n 1 ) 2 = H p2 (3-24)P
1 (n 2 / n 1 ) 3 = P 2 (3-25) Пример: законы о насосахНасос охлаждающей воды работает со скоростью 1800 об / мин. Его расход составляет 400 галлонов в минуту при напоре 48 футов. Мощность насоса составляет 45 кВт.Определите расход, напор и мощность насоса, если скорость насоса увеличится до 3600 об / мин.
Решение:
Расход
V˙ 2 = V˙ 1 (n 2 / n 1 )
= (400 галлонов в минуту) (3600 об / мин / 1800 об / мин)
= 800 г / мин
Напор
H p2 = H p1 (n 2 / n 1 ) 2
= 48 футов (3600 об / мин / 1800 об / мин) 2
= 192 футов
= 192 футовМощность
P 2 = P 1 (n 2 / n 1 ) 3
= 45 кВт (3600 об / 1800 об / мин) 3
= 360 кВт
Рисунок 8 : Изменение скоростей центробежного насосаМожно построить характеристическую кривую для новой скорости насоса на основе кривой для его исходной скорости.Метод состоит в том, чтобы взять несколько точек на исходной кривой и применить законы насоса для определения нового напора и расхода при новой скорости. Кривая зависимости напора от расхода, которая возникает в результате изменения скорости насоса, графически проиллюстрирована на Рисунке 8.
Характеристическая кривая системы
Рисунок 9: Типичная кривая потери напора в системе В главе, посвященной потере напора, было определено, что оба типа фрикционных потери и незначительные потери в трубопроводных системах были пропорциональны квадрату скорости потока.Поскольку скорость потока прямо пропорциональна объемному расходу, потеря напора в системе должна быть прямо пропорциональна квадрату объемного расхода. Исходя из этого соотношения, можно построить кривую потери напора в системе в зависимости от объемного расхода. Кривая потери напора для типичной системы трубопроводов имеет форму параболы, как показано на Рисунке 9.
Исходя из этого соотношения, можно построить кривую потери напора в системе в зависимости от объемного расхода. Кривая потери напора для типичной системы трубопроводов имеет форму параболы, как показано на Рисунке 9.
Рабочая точка системы
Рисунок 10: Рабочая точка для центробежного насосаТочка, в которой насос работает в данной системе трубопроводов, зависит от от расхода и потери напора этой системы.Для данной системы объемный расход сравнивается с потерями напора в системе на характеристической кривой. Построив график характеристической кривой системы и характеристической кривой насоса в одной и той же системе координат, можно определить точку, в которой насос должен работать. Например, на рисунке 10 рабочая точка центробежного насоса в исходной системе обозначена пересечением кривой насоса и кривой системы (h Lo ).
Система имеет расход, равный V˙ 0 , и полную потерю напора в системе, равную ∆P 0 .Для поддержания расхода V˙ 0 напор насоса должен быть равен ∆P o . В системе, описанной системной кривой (h L1 ), в системе был открыт клапан, чтобы уменьшить сопротивление системы потоку. В этой системе насос поддерживает большой расход (V˙ 1 ) при меньшем напоре насоса (∆P 1 ).
Система Использование нескольких центробежных насосов
Типичный центробежный насос имеет относительно небольшое количество движущихся частей и может быть легко адаптирован к различным первичным двигателям.Эти первичные двигатели включают электродвигатели переменного и постоянного тока, дизельные двигатели, паровые турбины и пневмодвигатели. Центробежные насосы, как правило, имеют небольшие размеры и могут быть изготовлены с относительно низкими затратами. Кроме того, центробежные насосы обеспечивают высокий объемный расход при относительно низком давлении.
Для увеличения объемного расхода в системе или для компенсации больших сопротивлений потоку центробежные насосы часто используются параллельно или последовательно.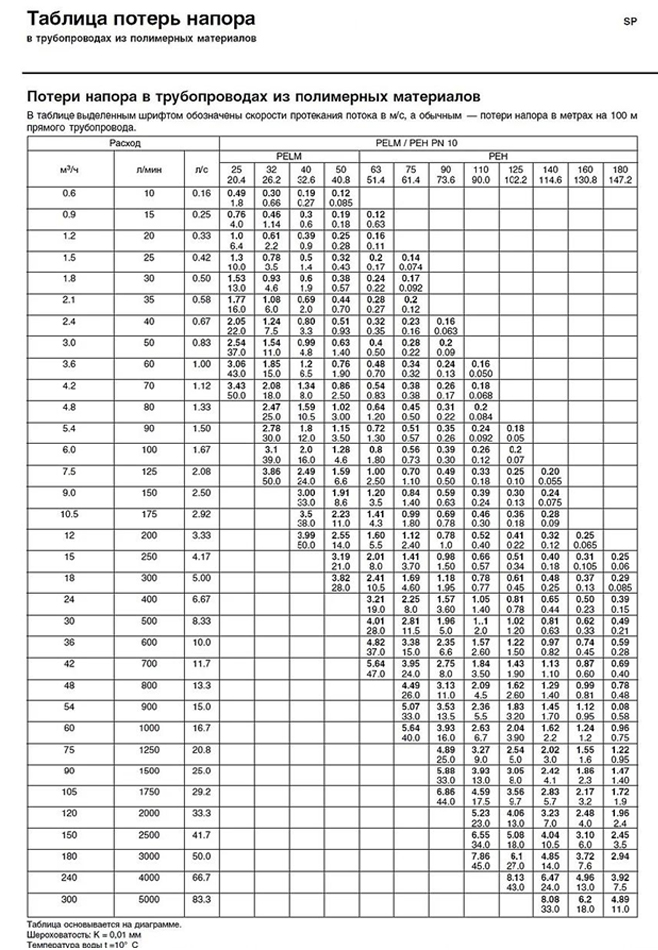 На рисунке 11 изображены два идентичных центробежных насоса, работающих параллельно с одинаковой скоростью.
На рисунке 11 изображены два идентичных центробежных насоса, работающих параллельно с одинаковой скоростью.
Центробежные насосы, подключенные параллельно
Поскольку вход и выход каждого насоса, показанные на рисунке 11, находятся в идентичных точках в системе, каждый насос должен производить один и тот же насос голова. Однако общий расход в системе является суммой индивидуальных расходов для каждого насоса.
Когда характеристическая кривая системы рассматривается с кривой для параллельных насосов, рабочая точка на пересечении двух кривых представляет более высокий объемный расход, чем для одиночного насоса, и большую потерю напора в системе.Как показано на Рисунке 12, большая потеря напора в системе происходит с увеличением скорости жидкости в результате увеличения объемного расхода. Из-за большего напора системы объемный расход фактически в два раза меньше расхода, достигаемого при использовании одного насоса.
Рисунок 12: Рабочая точка для двух параллельных центробежных насосовЦентробежные насосы в серии
Центробежные насосы используются последовательно для преодоления больших потерь напора в системе, чем один насос может компенсировать по отдельности.Как показано на Рисунке 13, два идентичных центробежных насоса, работающих с одинаковой скоростью и одинаковым объемным расходом, создают одинаковый напор. Поскольку вход второго насоса является выходом первого насоса, напор, создаваемый обоими насосами, является суммой отдельных напоров. Объемный расход от входа первого насоса до выхода второго остается прежним.
Рисунок 13: Кривая характеристик насоса для двух идентичных центробежных насосов, используемых в серии Как показано на Рисунке 14, использование двух насосов последовательно не увеличивает сопротивление потоку в системе вдвое.Два насоса обеспечивают достаточный напор для новой системы, а также поддерживают немного более высокий объемный расход.
Основные моменты этой главы кратко изложены ниже.
• Чистый положительный напор на всасывании — это разница между давлением всасывания насоса и давлением насыщения жидкости.
• Кавитация — это образование и последующее схлопывание пузырьков пара на рабочем колесе насоса, когда местное давление падает ниже, а затем поднимается выше давления насыщения перекачиваемой жидкости.
• Законы насоса можно использовать для определения влияния изменения скорости центробежного насоса на расход, напор и мощность.
V˙ 1 (n 2 / n 1 ) = V˙ 2 H p1 (n 2 / n 1 ) 2 = H p2 P 1 (n 2 / n 1 ) 3 = P 2• Кривая комбинированного насоса для двух центробежных насосов, подключенных параллельно, может быть определена путем сложения индивидуальные потоки для любой данной головы.
• Комбинированная характеристика насосов для двух последовательно включенных центробежных насосов может быть определена путем добавления отдельных напоров для любого заданного расхода.
• Рабочая точка (напор и расход) системы может быть определена путем построения кривой насоса и кривой потери напора системы на одних и тех же осях. Система будет работать на пересечении двух кривых.
Парадокс гидравлического сопротивления при быстром течении воды в узкой трубе
Экспериментальные результаты этого измерения для различных внутренних диаметров d трубы показаны в Таблице 1, которая содержит пять столбцов измеренной скорости поперечного сечения \ (v \ left (p \ right) \) по отношению к входному давлению p и внутренним диаметрам d = 0. {2}} , \ end {align} $$
{2}} , \ end {align} $$
(1)
где \ (\ lambda \) — коэффициент потерь на трение.Чтобы выразить коэффициент потерь на трение \ (\ lambda \), мы должны сформулировать серию уравнений относительно характера потока, который описывается числом Рейнольдса и относительной шероховатостью. Анализ экспериментальных данных в таблице 1 показывает, что исследуемый поток характеризуется числом Рейнольдса Re \ (\ gg \) 10 4 , что соответствует квадратичной области с интенсивной турбулентностью.
Гидравлические потери потока воды с вышеуказанными параметрами наилучшим образом вписываются в квадратичную область интенсивной турбулентности, которая описывается коэффициентом потерь фон Кармана — Никурадсе 5,6
$$ \ begin {align} \ lambda = { {\ left (2 \ log \ frac {d} {2 \ delta} +1.{2}} \ rightarrow v = \ sqrt {\ frac {2d \ Delta p} {\ rho L}} \ left (2 \ log \ frac {d} {2 \ delta} +1.14 \ right). \ end {align} $$
(3)
Предполагая нулевое давление на выходе из трубки в пустое пространство и пренебрегая влиянием сжатия на входе, потеря давления \ (\ Delta p \) равна входному давлению p на отверстии трубки и окончательная формула скорости для обоих параметров принимает вид
$$ \ begin {align} v \ left (p, d \ right) = \ sqrt {\ frac {2dp} {\ rho L}} \ left (2 \ log \ frac {d} {2 \ delta} +1.14 \ справа). \ end {align} $$
(4)
Рисунок 3Микрофотография внутренней стенки трубки, полученная с помощью сканирующего электронного микроскопа. Относительная шероховатость была проанализирована в разрезе с помощью Mitutoyo Surftest SJ-401 с полученными значениями в диапазоне 2–4%.
В конце рисунка 4 мы напрямую сравнили экспериментальные данные для давлений 6 МПа и 24 МПа из таблицы 1 с предсказанными теоретическими зависимостями \ (v \ left (d \ right) \) из уравнения (4).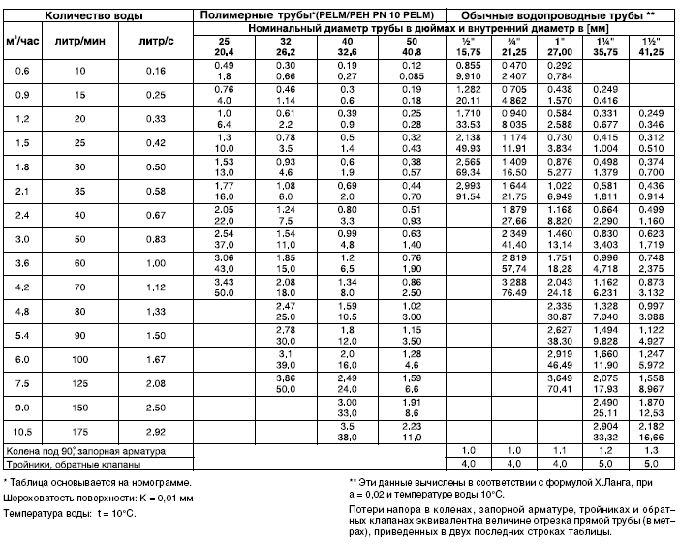 Мы ясно видим значительное отклонение при очень малых диаметрах <250 мкм для всех значений давления на входе. Для труб диаметром около 130 мкм скорость истечения приближается к максимальным теоретическим значениям без потерь энергии, вызванных сжатием и гидравлическим трением.
Мы ясно видим значительное отклонение при очень малых диаметрах <250 мкм для всех значений давления на входе. Для труб диаметром около 130 мкм скорость истечения приближается к максимальным теоретическим значениям без потерь энергии, вызванных сжатием и гидравлическим трением.
Экспериментально определенная зависимость средней скорости потока в поперечном сечении в трубе длиной 20 мм от внутреннего диаметра d для входного давления 24 МПа (квадратные точки) и 6 МПа (кружки), которые могут быть по сравнению с теоретическими кривыми по (4), где длинные и короткие пунктирные линии соответствуют 24 МПа и 6 МПа соответственно.Соответствующие горизонтальные линии представляют максимальные теоретические значения скорости истечения без потерь энергии, вызванных сжатием и трением для входного давления. Пунктирные соединители для обоих наборов данных вставлены только для обозначения сродства точек для данного значения давления и не представляют истинную зависимость между ними.
Длина турбулентного входа L h = 10d достигает значений в диапазоне 1,3–5 мм 7 . Из-за гораздо большей длины трубы L = 20 мм и экстремального характера потока очень проблематично рассматривать эффект длины входа как реалистичный параметр при возможном объяснении этого отклонения от теоретической экстраполяции (4).Одна из возможностей объяснить это парадоксальное поведение — это поверхностная кавитация на границе между текущей водой и сильно искривленной стенкой трубы. Такой режим потока описывал бы идеализированную модель коллективного движения водяного столба, отделенного от стенки кавитационным слоем газа и пара. Общеизвестно, что кавитация возникает на острой кромке входного отверстия сопла 8 . На входе в трубку (рис. 3) имеется ровный металлографический вырез, перпендикулярный ее оси, который образует острый край по внутренней окружности.Начало потока образует сразу за острой кромкой в области слабого сжатия очень тонкий слой поверхностной кавитации, который затем полностью окружает поток жидкости 9 . При высоких градиентах давления кавитационная оболочка очень быстро растягивается в направлении потока и за десятки \ (\ mu \) с достигает уровня выходного отверстия трубки 10 . После достижения уровня выпускного отверстия трубы открытый кавитационный слой заполняется воздухом, и возникает явление гидравлического переворота 9,10,11,12 .Гидравлический флип экспериментально изучался в нескольких публикациях, а именно в Cui et al. 11 и Sou et al. 12 . Куи и др. Провели эксперименты с максимальной длиной сопла 4 мм и минимальным диаметром 0,8 мм, что дает максимальное отношение L / d = 3,2. Sou et al. имел максимальную длину сопла 10 мм и минимальный диаметр 0,5 мм, что дает максимальное отношение L / d = 20. В качестве вклада в нашей статье мы рассматриваем экспериментальные данные о том, что гидравлический переворот происходит даже при очень высоких отношениях длины до диаметра L / d = 154, что значительно превышает значения в проведенных до сих пор экспериментах.Если столб жидкости движется в осевом направлении без контакта со стенкой трубы, возникает вопрос, как жидкость может сохранить свою радиальную стабильность в ожидаемой турбулентности, особенно в отношении турбулентных флуктуаций скорости в отдельных микрообъемах. На основе разложения Рейнольдса мгновенная скорость \ ({\ mathbf {u}} \ left ({\ mathbf {x}}, t \ right) \) в окрестности x может быть выражена как сумма временных средних \ ({{\ left \ langle {\ mathbf {u}} \ left ({\ mathbf {x}}, t \ right) \ right \ rangle} _ {t}} \) и составляющая колебаний \ (\ mathbf { {u} ‘} \ left ({\ mathbf {x}}, t \ right) \)
При высоких градиентах давления кавитационная оболочка очень быстро растягивается в направлении потока и за десятки \ (\ mu \) с достигает уровня выходного отверстия трубки 10 . После достижения уровня выпускного отверстия трубы открытый кавитационный слой заполняется воздухом, и возникает явление гидравлического переворота 9,10,11,12 .Гидравлический флип экспериментально изучался в нескольких публикациях, а именно в Cui et al. 11 и Sou et al. 12 . Куи и др. Провели эксперименты с максимальной длиной сопла 4 мм и минимальным диаметром 0,8 мм, что дает максимальное отношение L / d = 3,2. Sou et al. имел максимальную длину сопла 10 мм и минимальный диаметр 0,5 мм, что дает максимальное отношение L / d = 20. В качестве вклада в нашей статье мы рассматриваем экспериментальные данные о том, что гидравлический переворот происходит даже при очень высоких отношениях длины до диаметра L / d = 154, что значительно превышает значения в проведенных до сих пор экспериментах.Если столб жидкости движется в осевом направлении без контакта со стенкой трубы, возникает вопрос, как жидкость может сохранить свою радиальную стабильность в ожидаемой турбулентности, особенно в отношении турбулентных флуктуаций скорости в отдельных микрообъемах. На основе разложения Рейнольдса мгновенная скорость \ ({\ mathbf {u}} \ left ({\ mathbf {x}}, t \ right) \) в окрестности x может быть выражена как сумма временных средних \ ({{\ left \ langle {\ mathbf {u}} \ left ({\ mathbf {x}}, t \ right) \ right \ rangle} _ {t}} \) и составляющая колебаний \ (\ mathbf { {u} ‘} \ left ({\ mathbf {x}}, t \ right) \)
$$ \ begin {align} {\ mathbf {u}} \ left ({\ mathbf {x}}, t \ right) = {{\ left \ langle {\ mathbf {u}} \ left ({\ mathbf {x}}, t \ right) \ right \ rangle} _ {t}} + \ mathbf {{u} ‘ } \ left ({\ mathbf {x}}, t \ right), \ text {} {{\ left \ langle \ mathbf {{u} ‘} \ left ({\ mathbf {x}}, t \ right) \ right \ rangle} _ {t}} = 0.{\ text {fl}} \ left (V \ right).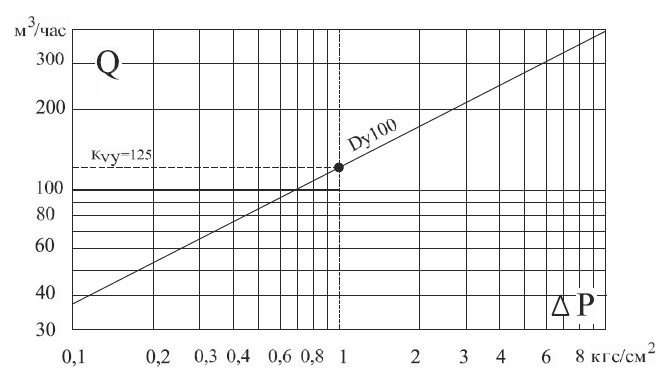 {\ text {tr}} \ left (V \ right).\ end {align} $$
{\ text {tr}} \ left (V \ right).\ end {align} $$
(8)
Следовательно, логическим выводом является отсутствие турбулентных колебаний скорости в столбе протекающей жидкости. В этой ситуации мы могли бы рассмотреть описание потока внутри колонны с помощью модели ламинарного профиля скорости в режиме скольжения. Однако максимальное значение в профиле оси трубы должно соответствовать теоретическому расходу, поэтому единственное приемлемое приближение модели кажется «идеальным скольжением», которое соответствует профилю постоянной скорости в режиме «поршневой поток».Зависимости чисел Рейнольдса от диаметра трубы (рис. 5) имеют примерно постоянный ход в пределах погрешности измерения в диапазоне диаметров 0,25–0,13 мм. С уменьшением диаметра расход приближается к режиму «поршневой» и достигает своего максимума около 0,13 мм (см. Рис. 4). В приемлемом приближении радиальная устойчивость столба жидкости обеспечивается постоянным профилем скорости без турбулентных пульсаций и вязкого трения. Связующее давление воды при очень малых диаметрах столба, которое может компенсировать динамику возможных радиальных колебаний давления, также можно рассматривать как дополнительный стабилизирующий эффект.Давление когезии было рассчитано примерно на 1,1 кПа на основе уравнения Лапласа-Юнга для диаметра колонки d = 0,13 мм. Реальное применение упомянутого эффекта стабилизации является весьма спорным при более низких расходах, но при дальнейшем уменьшении диаметра колонки ниже 0,13 мм можно ожидать увеличения значимости. Авторы осознают, что в статье не дается полностью точное количественное описание механизма потока, но наша основная цель — познакомить широкое гидравлическое сообщество с достигнутыми нами экспериментальными результатами и предложить возможное направление дальнейших исследований.Мы предполагаем, что дальнейшее детальное исследование быстрого течения в гладких капиллярах толщиной менее 0,1 мм может принести очень интересные приложения в области «микроструй» и в области высокоскоростной жидкости.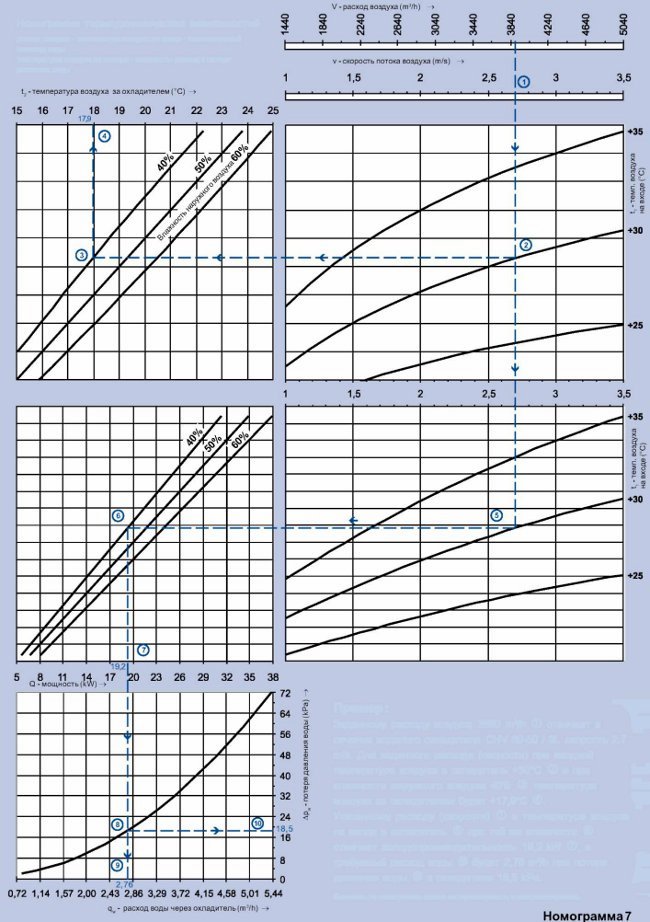
Экспериментальные точки \ (\ circ \) зависимости числа Рейнольдса Re в металлических трубках длиной 20 мм от внутреннего диаметра d для входного давления p = (6, 8, 10, 12, 14, 16, 18, 20, 22, 24) МПа из значений в таблице 1. При диаметре более 0,25 мм экспериментальные значения для 6 МПа и 24 МПа хорошо согласуются с теоретическим предсказанием уравнения Дарси – Вайсбаха с потерями Фон Кармана – Никурадсе. коэффициент (пунктирные линии).При возможной экстраполяции ниже 0,13 мм мы можем предположить, что скорость потока уже достигла постоянного теоретического максимума, а число Рейнольдса будет только линейной функцией диаметра d (пунктирные линии).
Анализ скорости ударной волны гидравлического удара подъемных труб для глубоководных горных работ
Bahrar, B., Rieutord, E., Morel, R. и Zeggwagh, G., 1998. Моделирование явления гидравлического удара относительно реального поведения трубы, La Houille Blanche — Revue Internationale de l’Eau , 53 (1): 18–25.(на французском языке)
Статья Google Scholar
Баттертон, С., 2006. Гидравлический удар: анализ водопроводных систем, проникновения и работы насосов , магистерская работа, Политехнический институт и университет штата Вирджиния, 23–35.
Google Scholar
Бергант, А., Тейсселинг, А.С., Витковски, Дж. П., Ковас, Д. И. К., Симпсон, А. Р. и Ламберт, М. Ф., 2008а. Параметры, влияющие на затухание, форму и синхронизацию волны гидроудара — Часть 1: Математические инструменты, IAHR Journal of Hydraulic Research , 46 (3): 373–381.
Артикул Google Scholar
Бергант, А., Тейсселинг, А.С., Витковски, Дж. П., Ковас, Д. И. К., Симпсон, А. Р. и Ламберт, М. Ф., 2008b. Параметры, влияющие на затухание, форму и синхронизацию волны гидроудара — Часть 2: Примеры из практики, IAHR Journal of Hydraulic Research , 46 (3): 382–391.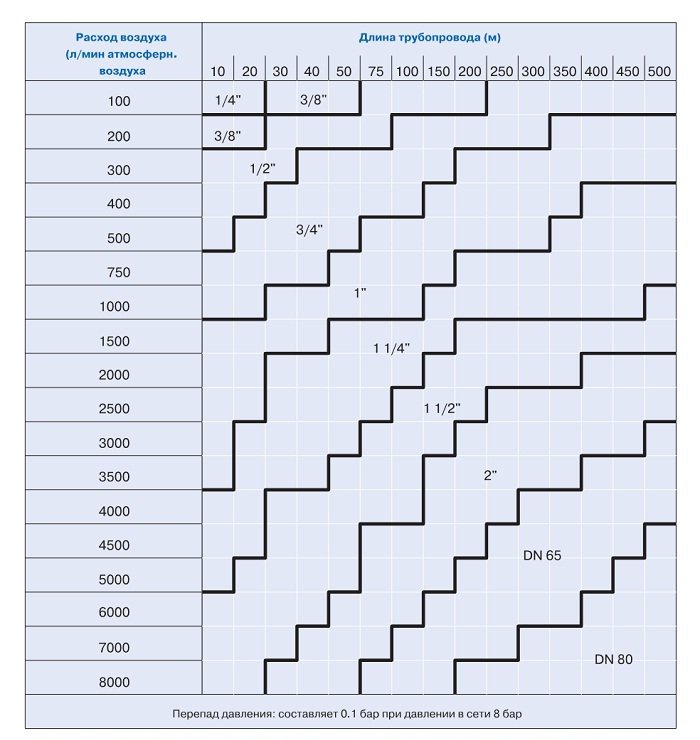
Артикул Google Scholar
Ковас, Д., Стоянов, И., Мано, Дж., Рамос, Х., Грэм, Н. и Максимович, К., 2005. Динамическое влияние вязкоупругости стенки трубы в гидравлических переходных процессах, Часть II. -Разработка, калибровка и проверка моделей, IAHR Journal of Hydraulic Research , 43 (1): 56–70.
Артикул Google Scholar
Дин, Х.D., 2006. Гидравлическая транспортировка по трубопроводу многометаллических конкреций морского дна, Гидравлическая добыча угля и трубопроводная транспортировка , 2 , 1–4. (на китайском языке)
Google Scholar
Han, WL, Dong, ZN, Chai, HE и Han, J., 2000. Вычисление уравнений гидравлического удара в псевдогомогенном потоке твердое тело-жидкость и их проверка, Science in China, Series E , 43 (2): 215–224.
MATH Google Scholar
Карни, Б.W. and Ghidaoui, M. S., 1992. Обсуждение сплайн-интерполяции для анализа гидравлического удара, J. Hydraul. Англ. , ASCE, 118 (11): 1597–1600.
Артикул Google Scholar
Li, QS, Yang, K. и Zhang, L., 2003. Аналитическое решение для взаимодействия жидкости и структуры в заполненных жидкостью трубах, подвергающихся гидравлическому удару, вызванному ударами, Journal of Engineering Mechanics , ASCE, 129 (12): 1408–1417.
Артикул Google Scholar
Leslie, DJ and Tijsseling, AS, 2000. Перемещающиеся неоднородности в теории гидроудара: затухание из-за трения, Труды 8-й Международной конференции по скачкам давления , опубликованные BHR Group, Cranfield, UK, и Professional Engineering Издательство, Бери-Сент-Эдмундс, Великобритания, 323–335.
Google Scholar
Шоу, Г., 1994. Моделирование и проверка системы течения твердой и жидкой фаз, Труды 31-го ежегодного собрания Группы интересов по моделированию трубопроводов , 1–6.
Google Scholar
Тейсселинг А. С. и Андерсон А., 2004. Уравнение Жуковского для жидкостей и твердых тел, Труды 9-й Международной конференции по скачкам давления , Соединенное Королевство, 739–751.
Google Scholar
Тейсселинг, А.С., Ламберт, М. Ф., Симпсон, А. С., Стивенс, Витковски, Дж. П. и Бергант, А., 2008. Расширенная теория гидроудара Скалака, Journal of Sound and Vibration , 310 , 718–728.
Артикул Google Scholar
Валеш, Ф., Моравка, Ш., Брепта, Р. и Черв, Дж., 1996. Распространение волны в толстом цилиндрическом стержне из-за продольного удара, Механика и инженерия материалов, Международный журнал JSME, серия A , 39 (1): 60–70.
Google Scholar
Варди, А.Е. и Браун, JMB, 2000. Эволюция волнового фронта в зависимости от трения, Труды 8-й Международной конференции по скачкам давления , опубликовано BHR Group, Cranfield, UK, и Professional Engineering Publishing, Bury St. Edmunds , Великобритания, 337–349.
Google Scholar
von Kries, J. 1883. Ueber die Beziehungen Druck und Geschwindingkeit, welche bei der wellenbewegung in elastischen Schlauchen bestechen Festschrift der 56.Versammlung deutscher Naturforscher und, Arzte , 67–88. (на немецком языке)
Google Scholar
Виггерт Д. К. и Тейсселинг А. С., 2001. Переходные процессы жидкости и взаимодействие жидкости и конструкции в гибких заполненных жидкостью трубопроводах, Обзоры прикладной механики ASME , 54 (5): 455–481.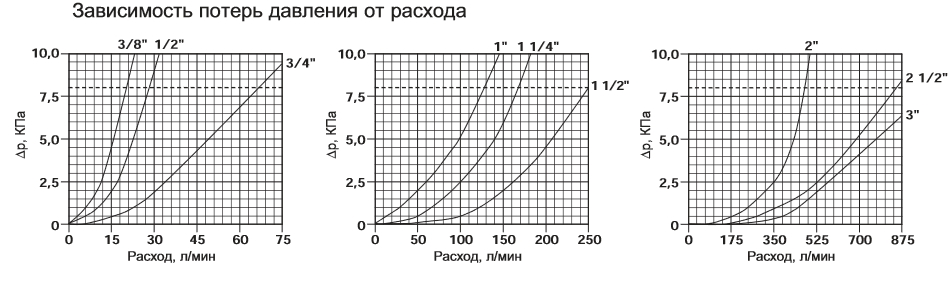
 9 — 8.2
9 — 8.2
