Т. Движение жидкостей — PhysBook
Зависимость давления жидкости от скорости ее течения
В предыдущих параграфах были рассмотрены законы равновесия жидкостей и газов. Теперь рассмотрим некоторые явления, связанные с их движением.
Движение жидкости называют течением, а совокупность частиц движущейся жидкости потоком. При описании движения жидкости определяют скорости, с которыми частицы жидкости проходят через данную точку пространства. Если в каждой точке пространства, заполненного движущейся жидкостью, скорость не изменяется со временем, то такое движение называется установившимся, или стационарным. При стационарном течении любая частица жидкости проходит через данную точку пространства с одним и тем же значением скорости. Мы будем рассматривать только стационарное течение идеальной несжимаемой жидкости. Идеальной называют жидкость, в которой отсутствуют силы трения.
Как известно, неподвижная жидкость в сосуде, согласно закону Паскаля, передает внешнее давление ко всем точкам жидкости без изменения. Но когда жидкость течет без трения по трубе переменного поперечного сечения, давление в разных местах трубы неодинаково. Оценить распределение давлений в трубе, по которой течет жидкость, можно с помощью установки, схематически изображенной на рисунке 1. Вдоль трубы впаивают вертикальные открытые трубки-манометры. Если жидкость в трубе находится под давлением, то в манометрической трубке жидкость поднимается на некоторую высоту, зависящую от давления в данном месте трубы. Опыт показывает, что в узких местах трубы высота столбика жидкости меньше, чем в широких. Это значит, что в этих узких местах давление меньше. Чем это объясняется?
Рис. 1
Предположим, что несжимаемая жидкость течет по горизонтальной трубе с переменным сечением (рис. 1). Выделим мысленно несколько сечений в трубе, площади которых обозначим
Пусть υ1 — скорость жидкости через сечение S1, υ2 — скорость жидкости через сечение S2. За время Δt объемы жидкостей, протекающих через эти сечения, будут равны:
\(~\begin{matrix} \Delta V_1 = l_1S_1 = \upsilon_1 \Delta t_1 \cdot S_1 ; \\ \Delta V_2 = l_2S_2 = \upsilon_2 \Delta t_2 \cdot S_2 . \end{matrix}\)Так как жидкость несжимаема, то ΔV1 = ΔV
Из этого уравнения \(~\frac{\upsilon_1}{\upsilon_2} = \frac{S_2}{S_1}\) , т.е. скорости жидкости в двух любых сечениях обратно пропорциональны площадям сечений. Это значит, что частицы жидкости при переходе из широкой части трубы в узкую ускоряются. Следовательно, на жидкость, поступающую в более узкую часть трубы, действует со стороны жидкости, еще находящейся в широкой части трубы, некоторая сила. Такая сила может возникнуть только за счет разности давлений в различных частях жидкости. Так как сила направлена в сторону узкой части трубы, то в широком участке трубы давление должно быть больше, чем в узком. Учитывая уравнение неразрывности, можно сделать вывод:
К этому выводу впервые пришел Д. Бернулли, поэтому данный закон называют законом Бернулли.
Применение закона сохранения энергии к потоку движущейся жидкости позволяет получить уравнение, выражающее закон Бернулли (приводим без вывода)\[~p_1 + \frac{\rho \upsilon^2_1}{2} = p_2 + \frac{\rho \upsilon^2_2}{2}\] — уравнение Бернулли для горизонтальной трубки.
Здесь p1 и p2 — статические давления, ρ — плотность жидкости. Статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю. Такое давление измерил бы манометр, движущийся вместе с потоком. Неподвижная монометрическая трубка с отверстием, обращенным навстречу потоку, измерит давление \(~p = p_1 + \frac{\rho \upsilon^2_1}{2}\).
Слагаемые \(~\frac{\rho \upsilon^2_1}{2}\) и \(~\frac{\rho \upsilon^2_2}{2}\) имеют, с одной стороны, размерность давления, с другой — размерность объемной плотности энергии, т. е. энергии, приходящейся на единицу объема. Действительно, \(~W_k = \frac{m \upsilon^2}{2}\), масса жидкости m = ρV. Если V = 1 м3, то \(~W_k = \frac{\rho \upsilon^2}{2}\). Поэтому \(~\frac{\rho \upsilon^2}{2}\) — называют динамическим давлением. Это кинетическая энергия потока в единичном объеме жидкости (объемная плотность энергии).
Если трубка не горизонтальная, то надо учитывать и гидростатическое давление жидкости. Уравнение Бернулли будет иметь вид:
\(~p_1 + \rho gh_1 + \frac{\rho \upsilon^2_1}{2} = p_2 + \rho gh_2 + \frac{\rho \upsilon^2_2}{2},\)где h1 и h2 — высоты, на которых находятся сечения S1 и S2.
Закон Бернулли лежит в основе принципа действия многих технических устройств и приборов: водоструйного насоса, пульверизатора, форсунки карбюратора. Закон Бернулли позволяет объяснить возникновение подъемной силы крыла самолета.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 106-108.
Связь давления и скорости в потоке
Связь давления и скорости в потоке жидкости — обратная: если в каком-то месте потока скорость увеличивается, то давление здесь малó, и, наоборот, там, где скорости невелики, давление повышенное. Эту закономерность объясним на основе уравнения Бернýлли.
Рассмотрим работу водоструйного насоса (см. рис. 11). На подходе по нагнетательному трубопроводу 1 поток рабочей жидкости имеет относительно небольшую скорость v1 и высокое избыточное давление pизб1. Проходя через соплó 2, поток сужается, скорость его резко возрастает до v2. Для дальнейших рассуждений запишем уравнение Бернýлли так:
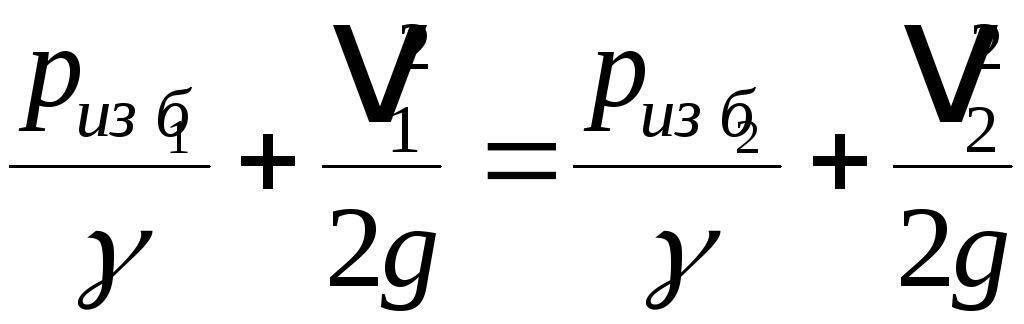 .
.
Здесь нет z1 и z2, так как труба горизонтальная, а величиной потерь напора DH» 0 пренебрегаем. Так как в правой части уравнения кинетическая составляющая энергии потока резко возросла из-за увеличения v2, то потенциальная составляющая, связанная с избыточным давлением после соплá pизб2, наоборот, уменьшится. Величину pизб2 можно выразить из этого уравнения и найти численное значение. Если pизб2 получается отрицательным, то, значит, возник вакуум (полное давление в струе стало меньше атмосферного). В последнем случае пьезометрическая линия опустится ниже отметки самой струи (см. рис 11).
Таким образом в струе рабочей жидкости после соплá образуется область пониженного давления или даже вакуум, что вызывает подсос транспортируемой жидкости по всасывающему трубопроводу 3 (см. рис. 11). Далее обе жидкости смешиваются в горловине 4 и транспортируются по отводящему трубопроводу 5.
Водоструйные насосы не имеют трущихся частей, в этом их преимущество перед механическими. По их принципу работают также эжекторы, гидроэлеваторы, насосы для создания вакуума.
Режимы движения жидкости
При проведении гидравлического расчёта в первую очередь нужно выяснять: какой режим движения будет наблюдаться у данного потока?
Режимы движения всех потоков (напорных и безнапорных) делятся на два типа (рис. 12):
1) ламинарный, то есть спокойный, параллельноструйный, при малых скоростях;
2) турбулентный, то есть бурлящий, вихреобразный, с водоворотами, при больших скоростях.
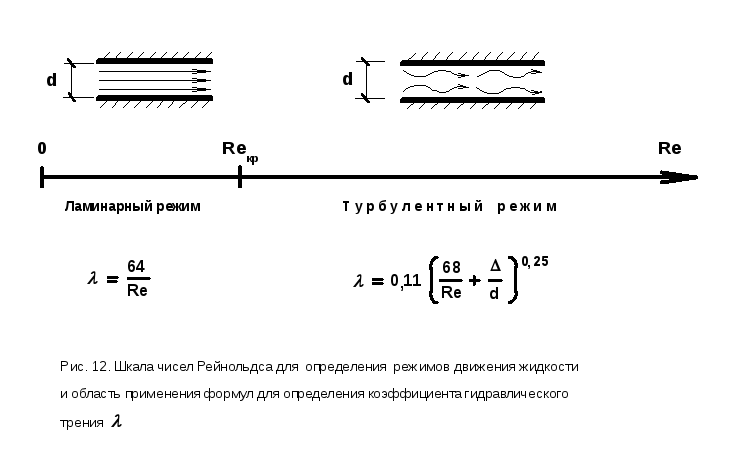
Для выяснения типа режима нужно рассчитать число Рейнольдса Re и сравнить его с критическим Reкр.
Число Рéйнольдса Re — это безразмерный критерий, вычисляемый по формулам:
— для напорных потоков
Re =vd/n ,
где d — внутренний диаметр напорного трубопровода;
— для безнапорных потоков
Re =vR/n,
где R — гидравлический радиус безнапорного потока, м (см. с. 14).
Критическое число Рейнольдса Reкр — это число Рейнольдса, при котором наступает смена режима движения.
Для напорных потоков
Reкр=2320,
для безнапорных потоков
Reкр » 500.
Упрощённо режим движения потока можно определить по шкале чисел Рейнольдса (см. рис. 12). Рассмотрим пример с напорной водопроводной трубой, у которой d=20 мм, v=1 м/с, n =10—6 м2/с. Для потока в данной трубе число Рейнольдса составит:
Re=1×0,02/10—6
Число 20000 больше, чем Reкр=2320 (для напорных потоков) и на рис.12 оно находится в правой части шкалы, следовательно, режим потока турбулентный и все дальнейшие гидравлические расчёты должны проводиться только по зависимостям и формулам для этого режима.
Зависимость скорости от давления воды в трубопроводе. Теория перекачивания жидкостей (Grundfos)
Зачем нужны подобные расчеты
При составлении плана по возведению большого коттеджа, имеющего несколько ванных комнат, частной гостиницы, организации пожарной системы, очень важно обладать более-менее точной информацией о транспортирующих возможностях имеющейся трубы, беря в учет ее диаметр и давление в системе. Все дело в колебаниях напора во время пика потребления воды: такие явления довольно серьезно влияют на качество предоставляемых услуг.

Кроме того, если водопровод не оснащен водосчетчиками, то при оплате за услуги коммунальных служб в расчет берется т.н. «проходимость трубы». В таком случае вполне логично выплывает вопрос о применяемых при этом тарифах.
При этом важно понимать, что второй вариант не касается частных помещений (квартир и коттеджей), где при отсутствии счетчиков при начислении оплаты учитывают санитарные нормы: обычно это до 360 л/сутки на одного человека.
От чего зависит проходимость трубы
От чего же зависит расход воды в трубе круглого сечения? Складывается впечатление, что поиск ответа не должен вызывать сложностей: чем большим сечением обладает труба, тем больший объем воды она сможет пропустить за определенное время. При этом вспоминается также давление, ведь чем выше водяной столб, тем с большей скоростью вода будет продавливаться внутри коммуникации. Однако практика показывает, что это далеко не все факторы, влияющие на расход воды.
Кроме них, в учет приходится брать также следующие моменты:
- Длина трубы . При увеличении ее протяженности вода сильнее трется об ее стенки, что приводит к замедлению потока. Действительно, в самом начале системы вода испытывает воздействие исключительно давлением, однако важно и то, как быстро у следующих порций появится возможность войти внутрь коммуникации. Торможение же внутри трубы зачастую достигает больших значений.
- Расход воды зависит от диаметра в куда более сложной степени, чем это кажется на первый взгляд. Когда размер диаметра трубы небольшой, стенки сопротивляются водному потоку на порядок больше, чем в более толстых системах. Как результат, при уменьшении диаметра трубы снижается ее выгода в плане соотношения скорости водного потока к показателю внутренней площади на участке фиксированной длины. Если сказать по-простому, толстый водопровод гораздо быстрее транспортирует воду, чем тонкий.
- Продолжительность службы . Со временем на стальных водопроводах появляется ржавчина. Кроме этого для стали, как и для чугуна, характерно постепенно накапливать известковые отложения. Сопротивляемость водному потоку трубы с отложениями гораздо выше, чем новых стальных изделий: эта разница иногда доходит до 200 раз. Кроме того, зарастание трубы приводит к уменьшению ее диаметра: даже если не брать в расчет возросшее трение, проходимость ее явно падает. Важно также заметить, что изделия из пластика и металлопластика подобных проблем не имеют: даже спустя десятилетия интенсивной эксплуатации уровень их сопротивляемости водным потокам остается на первоначальном уровне.
- Наличие поворотов, фитингов, переходников, вентилей способствует дополнительному торможению водных потоков.
Все вышеперечисленные факторы приходится учитывать, ведь речь идет не о каких-то маленьких погрешностях, а о серьезной разнице в несколько раз. В качестве вывода можно сказать, что простое определение диаметра трубы по расходу воды едва ли возможно.
Новая возможность расчетов расхода воды
Если использование воды осуществляется посредством крана, это значительно упрощает задачу. Главное в таком случае, чтобы размеры отве
Жидкость, давление, скорость – основы закона сантехники
Главная страница » Жидкость, давление, скорость – основы закона сантехники
Сантехника, казалось бы, не даёт особого повода вникать в дебри технологий, механизмов, заниматься скрупулёзными расчётами для выстраивания сложнейших схем. Но такое видение – это поверхностный взгляд на сантехнику. Реальная сантехническая сфера ничуть не уступает по сложности процессов и, также как многие другие отрасли, требует профессионального подхода. В свою очередь профессионализм – это солидный багаж знаний, на которых основывается сантехника. Окунёмся же (пусть не слишком глубоко) в сантехнический учебный поток, дабы приблизиться на шаг к профессиональному статусу сантехника.
СОДЕРЖИМОЕ ПУБЛИКАЦИИ :
Закон Паскаля
Если измерительное устройство (манометр) разместить под слоем жидкости на определенной глубине и направлять его чувствительный элемент в разные стороны, показания давления будут оставаться неизменными в любом положении манометра.
То есть давление жидкости никак не зависит от смены направления. Но давление жидкости на каждом уровне зависит от параметра глубины. Если измеритель давления перемещать ближе к поверхности жидкости, показания будут уменьшаться.
Соответственно, при погружении измеряемые показания будут увеличиваться. Причём в условиях удвоения глубины, параметр давления также удвоится.
 Закон Паскаля наглядно демонстрирует действие давления воды в самых привычных условиях для современного быта
Закон Паскаля наглядно демонстрирует действие давления воды в самых привычных условиях для современного бытаОтсюда логичный вывод: давление жидкости следует рассматривать прямо пропорциональной величиной для параметра глубины.
В качестве примера рассмотрим прямоугольный контейнер размерами 10х10х10 см., который заполнен водой на 10 см глубины, что по объёмной составляющей будет равняться 10 см3 жидкости.
Этот объём воды в 10 см3 весит 1 кг. Используя имеющуюся информацию и уравнение для расчёта, несложно вычислить давление на дне контейнера.
Например: вес столба воды высотой 10 см и площадью поперечного сечения 1 см2 составляет 100 г (0,1 кг). Отсюда давление на 1 см2 площади:
P = F / S = 100 / 1 = 100 Па (0,00099 атмосферы)
Если глубина столба воды утроится, вес уже будет составлять 3 * 0,1 = 300 г (0,3 кг), и давление, соответственно увеличится втрое.
Таким образом, давление на любой глубине жидкости равноценно весу столба жидкости на этой глубине, поделённому на площадь поперечного сечения столба.
 Давление водяного столба: 1 — стенка контейнера для жидкости; 2 — давление столба жидкости на донную часть сосуда; 3 — давление на основание контейнера; А, С — области давления на боковины; В — прямой водяной столб; Н — высота столба жидкости
Давление водяного столба: 1 — стенка контейнера для жидкости; 2 — давление столба жидкости на донную часть сосуда; 3 — давление на основание контейнера; А, С — области давления на боковины; В — прямой водяной столб; Н — высота столба жидкостиОбъем жидкости, создающей давление, называется гидравлический напор жидкости. Давление жидкости благодаря гидравлическому напору, также остаётся зависимым от плотности жидкости.
Сила тяжести
Гравитация — одна из четырех сил природы. Мощь гравитационной силы между двумя объектами зависит от массы этих объектов. Чем массивнее объекты, тем сильнее гравитационное притяжение.
Когда выливается вода из контейнера, гравитация Земли притягивает воду к земной поверхности. Можно наблюдать тот же самый эффект, если на разных высотах разместить два ведра воды и соединить их трубкой.
Достаточно задать ход жидкости в трубке из одного ведра в другой, после чего сработает сила гравитации, и процесс перелива продолжится самопроизвольно.
Гравитация, приложенные силы и атмосферное давление являются статическими факторами, которые в равной степени относятся к жидкостям, находящимся в покое или в движении.
Силы инерции и трения являются динамическими факторами, которые действуют только на жидкости в движении. Математическая сумма силы тяжести, приложенной силы и атмосферного давления, представляет собой статическое давление, полученное в любой зоне жидкости и в любой момент времени.
Статическое давление
Статическое давление существует в дополнение к любым динамическим факторам, которые также могут присутствовать одновременно. Закон Паскаля гласит:
Давление, создаваемое жидкостью, действует равноценно по всем направлениям и под прямым углом к содержащимся поверхностям.
Это определение касается только жидкостей, находящихся в полном покое или практически недвижимых. Определение справедливо также только для факторов, составляющих статический гидравлический напор.
Очевидно: когда скорость движения становится фактором, в расчёт берётся направление. Сила, привязанная к скорости, также должна иметь направление. Поэтому закон Паскаля, как таковой, не применяется к динамическим факторам мощности потока жидкости.
 Скорость движения потока зависит от многих факторов, включая послойное разделение жидкостной массы, а также сопротивление, создаваемое разными факторами
Скорость движения потока зависит от многих факторов, включая послойное разделение жидкостной массы, а также сопротивление, создаваемое разными факторамиДинамические факторы инерции и трения привязаны к статическим факторам. Скоростной напор и потери давления привязаны к гидростатическому напору жидкости. Однако часть скоростного напора всегда может быть преобразована в статический напор.
Сила, которая может быть вызвана давлением или напором при работе с жидкостями, необходима, чтобы начать движение тела, если оно находится в состоянии покоя, и присутствует в той или иной форме, когда движение тела заблокировано.
Поэтому всякий раз, когда задана скорость движения жидкости, часть ее исходного статического напора используется для организации этой скорости, которая в дальнейшем существует уже как напорная скорость.
Объем и скорость потока
Объем жидкости, проходящей через определённую точку в заданное время, рассматривается как объем потока или расход. Объем потока обычно выражается литрами в минуту (л/мин) и связан с относительным давлением жидкости. Например, 10 литров в минуту при 2,7 атм.
Скорость потока (скорость жидкости) определяется как средняя скорость, при которой жидкость движется мимо заданной точки. Как правило, выражается метрами в секунду (м/с) или метрами в минуту (м/мин). Скорость потока является важным фактором при калибровке гидравлических линий.
 Объём и скорость потока жидкости традиционно считаются «родственными» показателями. При одинаковом объёме передачи скорость может меняться в зависимости от сечения прохода
Объём и скорость потока жидкости традиционно считаются «родственными» показателями. При одинаковом объёме передачи скорость может меняться в зависимости от сечения проходаОбъем и скорость потока часто рассматриваются одновременно. При прочих равных условиях (при неизменном объеме ввода), скорость потока возрастает по мере уменьшения сечения или размера трубы, и скорость потока снижается по мере увеличения сечения.
Так, замедление скорости потока отмечается в широких частях трубопроводов, а в узких местах, напротив, скорость увеличивается. При этом объем воды, проходящей через каждую из этих контрольных точек, остаётся неизменным.
Принцип Бернулли
Широко известный принцип Бернулли выстраивается на той логике, когда подъем (падение) давления текучей жидкости всегда сопровождается уменьшением (увеличением) скорости. И наоборот, увеличение (уменьшение) скорости жидкости приводит к уменьшению (увеличению) давления.
Этот принцип заложен в основе целого ряда привычных явлений сантехники. В качестве тривиального примера: принцип Бернулли «виновен» в том, что занавес душа «втягивается внутрь», когда пользователь включает воду.
Разность давлений снаружи и внутри вызывает силовое усилие на занавес душа. Этим силовым усилием занавес и втягивается внутрь.
Другим наглядным примером является флакон духов с распылителем, когда нажимом кнопки создаётся область низкого давления за счёт высокой скорости воздуха. А воздух увлекает за собой жидкость.
 Принцип Бернулли для самолётного крыла: 1 — низкое давление; 2 — высокое давление; 3 — быстрое обтекание; 4 — медленное обтекание; 5 — крыло
Принцип Бернулли для самолётного крыла: 1 — низкое давление; 2 — высокое давление; 3 — быстрое обтекание; 4 — медленное обтекание; 5 — крылоПринцип Бернулли также показывает, почему окна в доме имеют свойства самопроизвольно разбиваться при ураганах. В таких случаях крайне высокая скорость воздуха за окном приводит к тому, что давление снаружи становится намного меньше давления внутри, где воздух остаётся практически без движения.
Существенная разница в силе попросту выталкивает окна наружу, что приводит к разрушению стекла. Поэтому когда приближается сильный ураган, по сути, следует открыть окна как можно шире, чтобы уравнять давление внутри и снаружи здания.
И ещё парочка примеров, когда действует принцип Бернулли: подъем самолёта с последующим полётом за счёт крыльев и движение «кривых шаров» в бейсболе.
В обоих случаях создаётся разница скорости проходящего воздуха мимо объекта сверху и снизу. Для крыльев самолета разница скорости создаётся движением закрылков, в бейсболе — наличием волнистой кромки.
Практика домашнего сантехника
ЧАРУЮЩИЕ ТАЙНЫ ЖИДКОСТИ | Наука и жизнь
Существует поразительная возможность овладеть предметом математически,
не понимая существа дела.
А. Эйнштейн
Эксперимент остается навсегда.
П. Л. Капица
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Тысячи лет люди наблюдают вечно изменчивое течение воды и пытаются разгадать ее тайну. Первоклассные физики и математики ломали и продолжают ломать головы, стараясь понять природу и прихотливое поведение потока воды. Но вступив в XXI век, мы с сожалением должны констатировать, что с конца XIX столетия — времени наивысшего расцвета науки о движении сплошных сред (гидродинамики в случае жидкости и аэродинамики в случае газа) — мы очень мало продвинулись в понимании природы этого вечно меняющегося течения. Все основные законы течения жидкости (для краткости везде будет говориться о жидкости, хотя, за некоторым исключением, те же закономерности присущи и газу) были открыты до первой половины XIX столетия. Перечислим их.
ПОСТОЯНСТВО ПОТОКА МАССЫ ЖИДКОСТИЕго еще называют законом неразрывности, законом непрерывности, уравнением сплошности жидкости или законом сохранения вещества в гидродинамике. По существу, этот закон был открыт Б. Кастелли в 1628 году. Он установил, что скорость течения жидкости в трубах обратно пропорциональна площади их поперечного сечения. Другими словами, чем уже сечение канала, тем с большей скоростью движется в нем жидкость.
ВЯЗКОСТЬ ЖИДКОСТИИ. Ньютон (конец XVII века) экспериментально установил, что любой жидкости свойственна вязкость, то есть внутреннее трение. Вязкость приводит к возникновению сил трения между движущимися с различными скоростями слоями жидкости, а также между жидкостью и омываемым ею телом. Им же было установлено, что сила трения пропорциональна коэффициенту вязкости жидкости и градиенту (перепаду) скорости потока в направлении, перпендикулярном его движению. Жидкости, подчиняющиеся этому закону, называют ньютоновскими в отличие от неньютоновских жидкостей, у которых зависимость между силой вязкого трения и скоростью жидкости имеет более сложный характер.
В силу вязкого трения скорость жидкости на поверхности омываемого ею тела всегда равна нулю. Это совсем не очевидно, но тем не менее подтверждается во множестве экспериментов.
Опыт. Убедимся, что скорость газа на поверхности обдуваемого им тела равна нулю.
Возьмем вентилятор и припудрим его лопасти пылью. Включим вентилятор в сеть и через несколько минут выключим. Пыль на лопастях как была, так и осталась, хотя вентилятор вращался с довольно большой скоростью и она должна была бы слететь.
Омывая лопасти вентилятора с большой скоростью, поток воздуха на их поверхности имеет нулевую скорость, то есть неподвижен. Поэтому пыль на них и остается. По этой же причине с гладкой поверхности стола легко можно сдуть крошки, а пыль приходится вытирать.
#1# ИЗМЕНЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ В ЗАВИСИМОСТИ ОТ СКОРОСТИ ЕЕ ДВИЖЕНИЯ.Д. Бернулли в своей книге «Гидродинамика» (1738) получил для идеальной жидкости, не обладающей вязкостью, математическую формулировку закона сохранения энергии в жидкости, который носит теперь название уравнения Бернулли. Оно связывает давление в потоке жидкости с ее скоростью и утверждает, что давление жидкости при ее движении меньше там, где сечение потока S меньше, а скорость жидкости соответственно больше. Вдоль трубки тока, которую можно мысленно выделить в спокойном безвихревом потоке, сумма статического давления , динамического ρV2/2, вызванного движением жидкости плотностью ρ, и давления ρgh столба жидкости высотой h остается постоянной:
#13#Это уравнение играет фундаментальную роль в гидродинамике, несмотря на то, что оно, строго говоря, справедливо только для идеальной, то есть не имеющей вязкости, жидкости.
#2#Опыт 1. Убедимся, что чем выше скорость воздуха, тем меньше давление в нем.
Зажжем свечу и через тонкую трубочку, например для коктейля, сильно дунем в нее так, чтобы струйка воздуха прошла примерно на расстоянии 2 см от пламени. Пламя свечи отклонится по направлению к трубочке, хотя на первый взгляд кажется, что воздух должен если и не задуть его, то по крайней мере отклонить в противоположную сторону.
#3# Лабораторный водоструйный насос. В струе воды из крана создается разрежение, которое выкачивает воздух из колбы.Почему? Согласно уравнению Бернулли, чем выше скорость потока, тем меньше давление в нем. Воздух выходит из трубочки с большой скоростью, так что давление в струе воздуха меньше, чем в окружающем свечу неподвижном воздухе. Перепад давления при этом направлен в сторону выходящего из трубочки воздуха, что и отклоняет к ней пламя свечи.
#4# Принцип работы пульверизатора: атмосферное давление выжимает жидкость в струю воздуха, где давление ниже.На этом принципе работают пульверизаторы, струйные насосы и автомобильные карбюраторы: жидкость втягивается в поток воздуха, давление в котором ниже атмосферного.
Опыт 2. Возьмем лист писчей бумаги за верхние края, поднесем его к стене и удержим на расстоянии примерно 3-5 см от стены. Подуем в промежуток между стеной и листом. Вместо того, чтобы отклониться от стенки, лист прижимается к ней за счет силы, которую может создавать только возникший перепад давления, направленный к стене. Значит, давление в струе воздуха между листом и стеной меньше, чем в неподвижном воздухе снаружи. Чем сильнее дуть в промежуток, тем плотнее будет прижиматься листок к стене.
#5#Уравнение Бернулли объясняет также классический опыт с трубой переменного сечения. В силу закона неразрывности для сохранения потока массы жидкости в суженной части трубы ее скорость должна быть выше, чем в широкой. Следовательно, давление выше там, где труба шире, и ниже там, где она уже. На этом принципе работает устройство для измерения скорости или расхода жидкости — трубка Вентури.
Падение внутреннего давления в потоке — хорошо проверенный экспериментальный факт, тем не менее он, вообще говоря, парадоксален. Действительно, интуитивно ясно, что жидкость, «протискиваясь» из широкой части трубы в узкую, «сжимается», а это должно привести к росту давления в ней. Такому поведению жидкости в настоящее время нет объяснения даже на молекулярном уровне, по крайней мере, автор его нигде не обнаружил.
#6# СОПРОТИВЛЕНИЕ, ИСПЫТЫВАЕМОЕ ТЕЛОМ ПРИ ДВИЖЕНИИ В ЖИДКОСТИСуществование сопротивления среды было обнаружено еще Леонардо да Винчи в XV столетии. Мысль, что сопротивление жидкости движению тела пропорционально скорости тела, впервые высказал английский ученый Дж. Уиллис. Ньютон во втором издании своей знаменитой книги «Математические начала натуральной философии» установил, что сопротивление состоит из двух членов, одного — пропорционального квадрату скорости и другого — пропорционального скорости. Там же Ньютон сформулировал теорему о пропорциональности сопротивления максимальной площади сечения тела, перпендикулярного направлению потока. Силу сопротивления тела, медленно движущегося в вязкой жидкости, рассчитал в 1851 году Дж. Стокс. Она оказалась пропорциональной коэффициенту вязкости жидкости, первой степени скорости тела и его линейным размерам.
Необходимо отметить, что сопротивление жидкости движущемуся в нем телу в значительной мере обусловливается именно наличием вязкости. В идеальной жидкости, в которой вязкость отсутствует, сопротивление вообще не возникает.
Опыт 1. Посмотрим, как возникает сопротивление движущегося в жидкости тела. Хотя в опыте тело неподвижно, а движется воздух, результата это не меняет. Какая разница, что движется — тело в воздухе или воздух относительно неподвижного тела?
#7#Возьмем свечу и коробок спичек. Зажжем свечу, поставим перед ней на расстоянии примерно 3 см коробок и сильно дунем на него. Пламя свечи отклоняется к коробку. Это означает, что позади коробка давление стало меньше, чем позади свечи, и разность давлений направлена по движению потока воздуха. Следовательно, тело при движении в воздухе или жидкости испытывает торможение.
Поток воздуха набегает на переднюю поверхность коробка, огибает его по краям и не смыкается позади, а отрывается от препятствия. Поскольку давление воздуха меньше там, где его скорость выше, давление по краям коробка меньше, чем позади него, где воздух неподвижен. Позади коробка возникает разность давлений, направленная от центра к его краям. В результате воздух за коробком устремляется к его краям, образуя завихрения, что и приводит к уменьшению давления.
Сопротивление зависит от скорости движения тела в жидкости, свойств жидкости, формы тела и его размеров. Важную роль в создании сопротивления играет форма задней стороны движущегося тела. Позади плоского тела возникает пониженное давление, поэтому сопротивление можно уменьшить, предотвратив срыв потока. Для этого телу придают обтекаемую форму. Поток плавно огибает тело и смыкается непосредственно за ним, не создавая области пониженного давления.
Опыт 2. Чтобы продемонстрировать различный характер обтекания, а следовательно, и сопротивле ния тел различной формы, возьмем шар, например мяч для пинг-понга или тенниса, приклеим к нему бумажный конус и поставим за ним горящую свечу.
#8#Повернем тело шариком к себе и подуем на него. Пламя отклонится от тела. Теперь повернем тело к себе острым концом и снова подуем. Пламя отклоняется к телу. Этот опыт показывает, что форма задней поверхности тела определяет направление перепада давления позади нее, а следовательно , и сопротивление тела в потоке воздуха.
В первом опыте пламя отклоняется от тела; это означает, что перепад давления направлен по потоку. Струя воздуха плавно обтекает тело, смыкается за ним и далее движется обычной струей, которая отклоняет пламя свечи назад и может даже задуть его. Во втором опыте пламя отклоняется к телу — как и в эксперименте с коробком, позади тела создается разрежение, перепад давления направлен против потока. Следовательно, в первом опыте сопротивление тела меньше, чем во втором.
ПАДЕНИЕ ДАВЛЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ ПРИ ЕЕ ДВИЖЕНИИ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯОпыт показывает, что давление в жидкости, текущей по трубе постоянного сечения, падает вдоль трубы по течению: чем дальше от начала трубы, тем оно ниже. Чем уже труба, тем сильнее падает давление. Это объясняется наличием вязкой силы трения между потоком жидкости и стенками трубы.
Опыт. Возьмем резиновую или пластиковую трубку постоянного сечения и такого диаметра, чтобы ее можно было насадить на носик водопроводного крана. Сделаем в трубке два отверстия и откроем воду. Из отверстий начнут бить фонтанчики, причем высота ближнего к крану фонтанчика будет заметно выше, чем расположенного дальше по потоку. Это показывает, что давление воды в ближайшем к крану отверстии выше, чем в дальнем: оно падает вдоль трубы в направлении потока.
#9#Объяснение этого явления на молекулярном уровне автору не известно. Поэтому приведем классическое объяснение. Выделим в жидкости маленький объем, ограниченный стенками трубки и двумя сечениями слева и справа. Так как жидкость течет по трубке равномерно, то разность давлений слева и справа от выделенного объема должна быть уравновешена силами трения между жидкостью и стенками трубки. Следовательно, давление справа, в направлении потока жидкости, будет меньше давления слева. Отсюда заключаем, что давление жидкости уменьшается в направлении течения воды.
На первый взгляд приведенное объяснение удовлетворительно. Однако возникают вопросы, ответа на которые пока нет.
1. Согласно уравнению Бернулли, уменьшение давления в жидкости при ее движении вдоль трубы должно означать, что скорость ее, наоборот, должна расти вдоль потока, то есть течение жидкости должно ускоряться. Но этого не может быть в силу закона неразрывности.
2. Силы трения между стенками трубы и жидкостью должны в принципе тормозить ее. Если это так, то при торможении скорость жидкости вдоль канала должна падать, что в свою очередь приведет к росту давления в ней по потоку. Однако внешнее давление, прокачивающее жидкость по трубе, компенсирует силы трения, заставляя жидкость течь равномерно с одинаковой по всему каналу скоростью. А раз так, то и давление жидкости вдоль канала должно быть везде одинаковым.
Итак, налицо экспериментальный факт, который легко проверить, однако объяснение его остается открытым.
ЭФФЕКТ МАГНУСАРечь идет о возникновении силы, перпендикулярной потоку жидкости при обтекании ею вращающегося тела. Этот эффект был обнаружен и объяснен Г. Г. Магнусом (около середины XIX столетия) при изучении полета вращающихся артиллерийских снарядов и их отклонения от цели. Эффект Магнуса состоит в следующем. При вращении летящего тела близлежащие слои жидкости (воздуха) увлекаются им и также получают вращение вокруг тела, то есть начинают циркулировать вокруг него. Встречный поток рассекается телом на две части. Одна часть направлена в ту же сторону, что и циркулирующий вокруг тела поток; при этом происходит сложение скоростей набегающего и циркулирующего потоков, значит, давление в этой части потока уменьшается. Другая часть потока направлена в сторону, противоположную циркуляции, и здесь результирующая скорость потока падает, что приводит к увеличению давления. Разность давлений с обеих сторон вращающегося тела и создает силу, которая перпендикулярна к направлению встречного, набегающего потока жидкости (воздуха).
#10#Опыт. Склеим из листа плотной бумаги цилиндр. Из доски, положенной одним краем на стопку книг, сделаем на столе наклонную плоскость и положим на нее цилиндр. Скатившись, он вроде бы должен дальше двигаться по параболе и упасть дальше от края. Однако вопреки ожидаемому траектория его движения загибается в другую сторону, и цилиндр залетает под стол. Все дело в том, что он не просто падает, а еще и вращается, создавая вокруг себя циркуляцию воздуха. Возникает избыточное давление, направленное в сторону, противоположную поступательному движению цилиндра.
#11#Эффект Магнуса позволяет игрокам в пинг-понг и теннис отбивать «крученые» мячи, а футболистам — посылать «сухой лист», ударяя мяч по краю.
ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ ПОТОКИОпыт обнаруживает две совершенно разные картины движения жидкости. При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела. До сих пор не ясно, возникают ли вихри с самого начала и имеют просто очень малые размеры, не видимые нами, или вихри возникают начиная с некоторой скорости движения жидкости.
Опыт. Посмотрим, как происходит переход ламинарного потока в турбулентный. Откроем кран и пустим воду сначала тоненькой струйкой, а потом все сильнее и сильнее (конечно, так, чтобы не затопить соседей). Тоненькая струйка движется плавно и спокойно. По мере того, как увеличивается напор воды, скорость струи растет, и, начиная с некоторого момента, вода в ней начинает закручиваться — возникают вихри. Появляясь сначала только в ограниченной области струи, с ростом напора вихри в конце концов охватывают все течение — оно становится турбулентным.
#12# Струя воды падает в поле тяжести, испытывая ускорение. Как только скорость течения возрастает настолько, что число Рейнольдса превышает критическое значение, ламинарное течение (вверху) переходит в турбулентное. Для данного течения Re»2300.Оценить скорость течения жидкости или газа, при которой возникает турбулентность, можно при помощи так называемого числа Рейнольдса Re = ρvl/μ, где ρ — плотность жидкости или газа, μ — их вязкость (вязкость воздуха, например, 18,5.10-6 Па.с; воды — 8,2.10-2 Па.с), v — скорость потока, l — характерный линейный размер (диаметр трубы, длина обтекаемого тела и пр.). Для каждого вида течений существует такая критическая величина Reкр, что при Re<Reкр возможно только ламинарное течение, а при Re>Reкр оно может стать турбулентым. Если измерить скорость течения воды из крана или вдоль желоба, то, исходя из приведенных значений, можно самим определить, при каком значении Reкр в потоке начинает развиваться турбулентность. Оно должно быть порядка 2000.